| 隧道近景影像特征点提取方法分析 |
2. 西南交通大学地球科学与环境工程学院,四川 成都, 610031;
3. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都, 610031;
4. 株洲中车时代电气股份有限公司,湖南 株洲, 412001
2. Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu 610031, China;
3. State-Province Joint Engineering Laboratory of Spatial Information Technology for High-Speed Railway Safety, Chengdu 610031, China;
4. Zhuzhou CRRC Times Electric Co., Ltd., Zhuzhou 412001, China
在近景摄影测量中,影像特征点准确提取是影像解析的关键技术,同时也是影像匹配、测量、建模的基础。现阶段基于图像灰度的点特征提取算法发展成熟,常用的点特征提取算子主要有Moravec算子、Harris算子、Förstner算子等。但相关理论及优化研究主要集中在航空影像与卫星遥感影像等领域[1-4], 针对隧道近景影像应用较少。由于隧道洞内测量环境较差且洞身狭长,会导致影像质量低且变形较大。另外,影像之间灰度相似度较高、重复纹理特征较多等原因会导致特征点提取与匹配过程中正确率较低等问题。
本文对基于影像灰度的特征点提取算法:Moravec算子、Harris算子、Förstner算子进行性能比较。以某隧道真实拍摄影像为例,分别从提取特征点个数、精度以及稳定性三方面对提取算法进行比较分析。比较各算子的优缺点,为隧道近景测量提供一定的参考和借鉴。
Moravec算子是利用灰度方差进行点特征提取[5]。首先计算4个方向的灰度差平方和,选择最小值作为该像元的角点响应值。其次,根据影像的特点设定一个经验阈值,将角点兴趣值大于经验阈值的像素点作为候选点, 最后通过选取候选点中的极值点作为特征点。Harris算子作为Moravec算子的改进算法[6],其主要对图像旋转平移和影像噪声具有较高的稳定性。
Förstner算子是通过计算影像各像素的Robert梯度和像素为中心的窗口灰度协方差矩阵[7],在影像中搜寻小且接近圆的误差椭圆点作为特征点。
通过兴趣算子所提取的特征点应具有以下4个特点:①特征点必须在邻域内具有唯一性并且区分于背景;②特征点必须独立于几何变形和辐射变形;③特征点具有全局独立性且对噪声和误差具有稳定性;④在提取过程中明确兴趣值的定义,便于后续图像分析与理解[8, 9]。Schmid等通过对现有方法进行总结,得出评价某兴趣算子的优劣应以所提取的特征点重复率以及信息量作为标准。本次实验采用某品牌普通数码相机进行影像拍摄,结合隧道工程的特殊环境,分别从特征点数量、精度、适应性3个方面进行定量比较。
1 提取个数对比分析本文分别使用上述3种提取算子对同一影像进行特征点提取,分别设置不同参数,对比分析提取数量以及分布情况。Moravec算子的提取结果如图 1、图 2所示。由图 1、图 2可知, 不同阈值对Moravec算子提取特征点个数影响较大,总体随着阈值增大而提取数量减少。另外此算法只考虑了同一像素4个方向上的灰度方差,因此特征点在灰度变化剧烈区域分布较为集中。
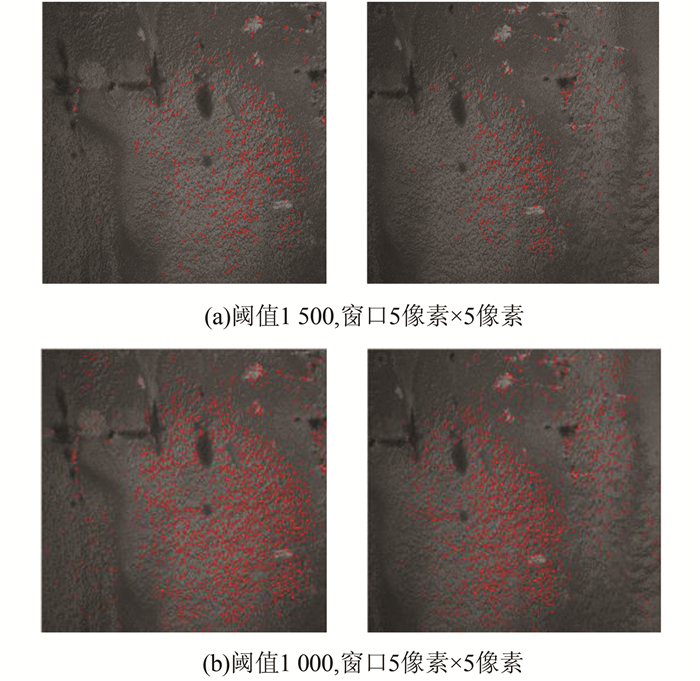 |
| 图 1 Moravec算子提取结果 Figure 1 Results of Moravec Operator |
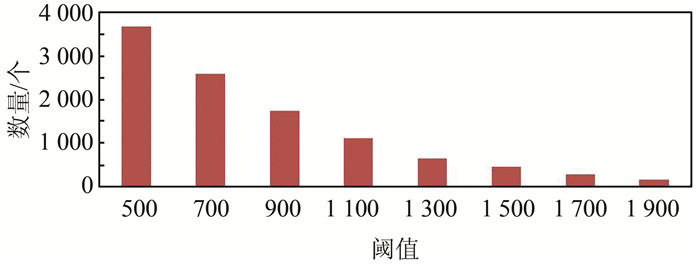 |
| 图 2 不同阈值Moravec算子提取结果 Figure 2 Number of the Feature Points of Moravec Operator in Different Thresholds |
Förstner算子提取结果如图 3、图 4所示,该算子提取特征点同样存在分布不均匀情况,并且权均值倍数对特征点个数的影像也较大,需要通过不断试验来确定阈值的范围。
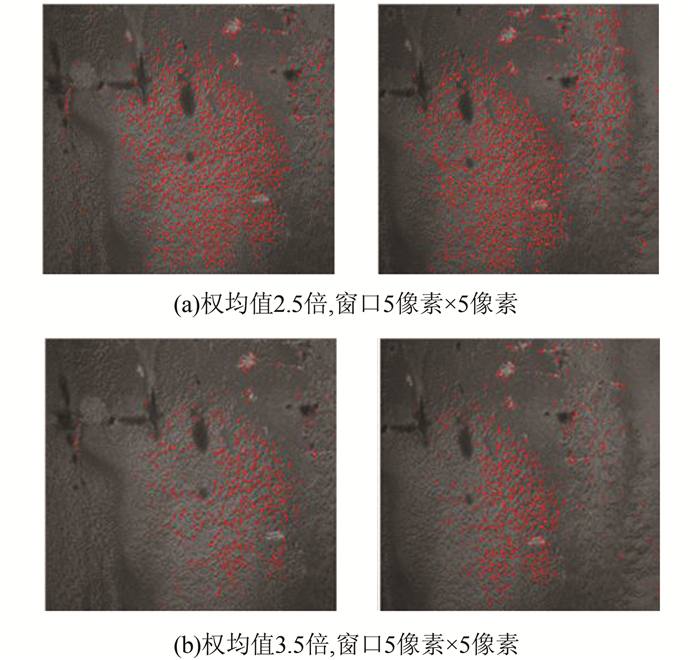 |
| 图 3 Förstner算子提取结果 Figure 3 The Results of Förstner Operator |
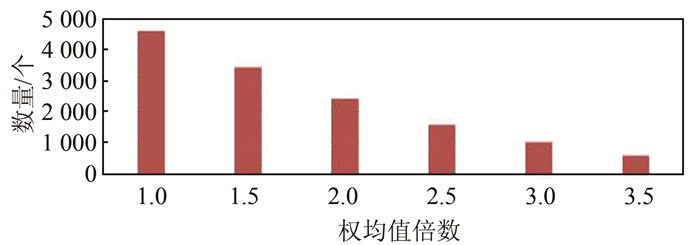 |
| 图 4 Förstner算子各权值倍数提取特征点数量 Figure 4 Number of the Feature Points of Förstner Operator in Different Weights |
Harris算子在计算过程中对影像进行了一阶灰度差分以及梯度值高斯滤波,并且顾及了像素点任意方向的灰度变化,所提取的特征点分布较为均匀(图 5、图 6)。提取的特征点个数随高斯σ增大而增大,但到一定数值时,σ的增加对特征点提取个数影响较小。
 |
| 图 5 Harris算子提取结果 Figure 5 Results of Harris Operator |
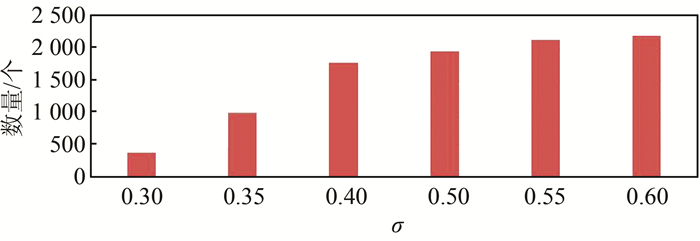 |
| 图 6 Harris算子各σ值提取特征点个数 Figure 6 The Number of the Feature Points of Harris Operator in Different Gauss Variance |
2 精度比较实验
由于隧道壁上灰度相似度高,且无明显辨别的特征点。为验证上述算子提取特征点的定位精度,以黑白相间标靶纸中的角点当作明显辨别的特征点对算子提取影像特征点的位置进行定位精度评定。定位精度通过以下指标进行评定[10]:
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {\left[ {{{\left( {{x_i} - {X_i}} \right)}^2} + {{\left( {{y_i} - {Y_i}} \right)}^2}} \right]} }}{N}} $ | (1) |
| $ {X_{{\rm{RMSE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{x_i} - {X_i}} \right)}^2}} }}{N}} $ | (2) |
| $ {Y_{{\rm{RMSE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^N {{{\left( {{y_i} - {Y_i}} \right)}^2}} }}{N}} $ | (3) |
标靶图像中采用自主研发的影像量测工具,取两次结果平均值为图像坐标系下真值,其提取结果如图 7。对结果采用上述精度指标进行评定,如表 1。
 |
| 图 7 不同算子提取角点效果 Figure 7 Corner Detection Results of Different Operators |
| 表 1 特征提取算子精度/像素 Table 1 Precision of the Operators/piels |
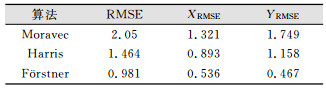 |
Förstner算法提取特点的精度最高,可达到子像素级;Harris算法次之;而Moravec算法最差。从图 7可以看出,Förstner算法提取的特征点大部分为角点,对边缘点识别差,Moravec算法和Harris算法对角点及边缘点识别较好。
3 适应性对比实验在本次实验中,分别对影像进行噪声添加、旋转变换以及对比度变化。统计在不同条件下算子的稳定性。实验中特征点重复率定义为影像经处理以及未经处理所提取的限差范围内特征点个数比值。
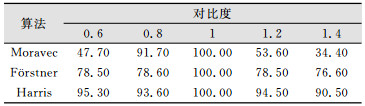
1) 对比度变化实验。采用对比度增强函数对原影像进行转化,分别得到对比度为:0.6、0.8、1、1.2、1.4的5幅影像(图 8)。使用上述3种特征点提取算子对其进行提取,其重复率如表 2所示。
 |
| 图 8 不同对比度下影像 Figure 8 Different Contrast Image |
| 表 2 不同对比度下影像重复率统计结果/% Table 2 Results of Image Repetition Rate in Different Contrast/% |
 |
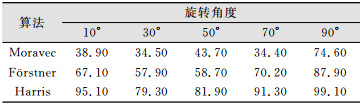
2) 旋转变化实验。采用旋转函数对原影像逆时针分别旋转10°、30°、50°、70°、90°,如图 9所示。同时采用3种算子对其进行特征点提取,计算重复率如表 3所示。
 |
| 图 9 不同旋转角度影像 Figure 9 Images in Different Rotation Angles |
| 表 3 不同旋转角度下影像重复率/% Table 3 Image Repetition Rate in Different Rotation Angles/% |
 |
3) 抗噪实验。使用Imnosie函数分别给影像加入0.01、0.02、0.03、0.04、0.05的椒盐噪声,得到的影像如图 10所示,对其进行特征点提取,其重复率如表 4所示。
 |
| 图 10 不同量椒盐噪声下的隧道影像 Figure 10 Tunnel Images in Different Noise |
| 表 4 不同量椒盐噪声影响重复率对比/% Table 4 Image Repetition Rate in Different Noise/% |
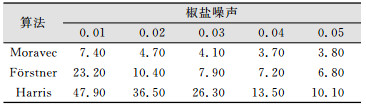 |
从对比变化以及旋转变化结果可知,Harris算子对不同对比度、旋转度的影像均能较好适应,重复率稳定,Förstner算子次之,Moravec算子最差。由于隧道洞内测量环境不一,在亮度变化较大的环境下,应选用Förstner算子以及Harris算子进行特征点提取。Moravec算子和Förstner算子对旋转角度较为敏感,在洞内进行拍摄时,应注意拍摄旋转角度,尽量保持小旋转角度。隧道洞内处于相对密封状态,在施工或过车等情况下会造成粉尘较大情况。3种算子对噪声响应敏感,噪声存在会极大降低特征点提取的正确率。因此,在隧道获取影像时,应尽量选择粉尘较少时段或在特征点提取前进行去噪处理。
4 结束语隧道内洞身狭长与影像间灰相似度高导致了隧道近景影像的特殊性,本文在介绍3种基本特征点提取算子的基础上,以某隧道影像为例,测评出各算子的提出数量、定位准确性以及适应稳定性,比较得到各算子在隧道洞内环境下的优缺点。本研究可以为今后隧道影像特征点的提取算法选择提供一定的参考价值。
| [1] |
王启春, 郭广礼, 查剑锋, 等. 基于图像灰度点特征提取算子的比较研究及改进[J]. 大地测量与地球动力学, 2012, 32(2): 148-154. |
| [2] |
谢轶群, 朱红春, 汤国安, 等. 基于DEM的沟谷特征点提取与分析[J]. 地球信息科学学报, 2013, 15(1): 61-67. |
| [3] |
邓非, 胡玉雷, 黄云. 一种基于SURF算法的柱面全景影像拼接方法[J]. 测绘地理信息, 2015, 40(4): 14-18. |
| [4] |
袁修孝, 陈时雨. 倾斜航摄影像匹配方法探究[J]. 测绘地理信息, 2015, 40(6): 1-6. |
| [5] |
康永辉, 戴激光, 关小东. 基于RFM的高分辨率卫星影像三维重建方法[J]. 测绘工程, 2014, 23(6): 33-37. DOI:10.3969/j.issn.1006-7949.2014.06.008 |
| [6] |
胡小青, 程朋根, 陈晓勇, 等. 基于邻域投票和Harris-SIFT特征的低空遥感影像匹配[J]. 测绘工程, 2016, 25(2): 33-37. DOI:10.3969/j.issn.1006-7949.2016.02.007 |
| [7] |
贺一楠, 耿娟, 秦军, 等. 结合Förstner与NCC约束的UAV图像配准研究[J]. 国土资源遥感, 2015, 27(1): 48-54. |
| [8] |
Schmid C, Mohr R, Bauckhage C. Evaluation of Interest Point Detectors[J]. International Journal of Computer Vision, 2000, 37(2): 151-172. DOI:10.1023/A:1008199403446 |
| [9] |
Rodehorst V, Koschan A. Comparison and Evaluation of Feature Point Detectors[C].The 5th International Symposium Turkish-German Joint Geodetic Days"Geodesy and Geoinformation in the Service of our Daily Life", Berlin, Germany, 2006
|
| [10] |
张春美.特征点提取及其在图像匹配中的应用研究[D].郑州: 信息工程大学, 2008
|
 2018, Vol. 43
2018, Vol. 43

