| 一种改进的基于对数路径损耗模型的WiFi定位方法 |
2. 同济大学测绘与地理信息学院,上海,200092
2. College of Surveying and Geo-Informatics, Tongji University, Shanghai 200092, China
近些年,室内定位技术发展迅速,如无线保真(wireless fidelity,WiFi)、红外线(infrared)、超带宽无线电(ultra wide band,UWB)等技术。在WiFi定位技术中,接收信号强度(received signal strength indication,RSSI)测距原理是将收发设备间的信号强度的衰减利用经验模型或理论模型转化为相应的信号传输的距离[1]。但RSSI的时变特征及不可预知的环境影响,使得基于此技术实现高精度的定位很难[2]。
在基于WiFi技术的室内定位中,本文考虑AP(access points)位置本身存在的误差并顾及每个AP随机噪声的影响,设计了基于混合最小二乘的AP信号特征定权的定位算法来改进传统的对数路径损耗模型,并用实测数据对定位效果进行了验证。
1 对数路径损耗模型参数的混合最小二乘解基于WiFi的信号传播模型定位法只需要相应的软件能接收、显示或提取出信号强度,不需要额外的设备[3],信号传播模型常采用统计模型进行分析[4]。当认为定位过程中系统硬件不存在损耗[5],且信号发射端和接收端的天线增益相同时,室内信号传播的模型就被认为是对数路径损耗模型[6]:
| $ R\left( d \right) = {R_0}\left( {{d_0}} \right) - 10n{\rm{lg}}\left( {\frac{d}{{{d_0}}}} \right) + {X_\sigma } $ | (1) |
为了求得对数路径损耗模型中每个AP的两个模型参数R0(d0)[7]和信号强度随距离增大而减小的衰减因子n[8],对AP发射出的信号在不同距离的m个位置进行k次信号强度采集[9]。
考虑到在实际测试的过程中,人为摆放的AP位置会有一定程度的误差,从而导致待定位点与AP之间的距离也存在误差[10]。因而,此时使用混合最小二乘法来求解每个AP的1 m处信号强度大小R0(d0)以及路径衰减因子n。
混合最小二乘的线性模型可以表示为:
| $ \mathit{\boldsymbol{A\beta }} = \left[ {{\mathit{\boldsymbol{A}}_1}\ \ \ {\mathit{\boldsymbol{A}}_2}} \right]\left[ {{\rm{ }}\begin{array}{*{20}{c}} {{R_0}({d_0})}\\ n \end{array}} \right] = \mathit{\boldsymbol{y}} $ | (2) |
对增广矩阵C进行正交三角分解和奇异值分解,则可得路径衰减因子n以及1 m处信号强度大小R0(d0)的混合最小二乘解为:
| $ \left[ {\begin{array}{*{20}{c}} {{R_0}\left( {{d_0}} \right)}\\ n \end{array}} \right] = {\left[ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}} - \sigma _2^2\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{I}} \end{array}} \right]} \right]^{ - 1}}{A^{\rm{T}}}\mathit{\boldsymbol{Py}} $ | (3) |
考虑AP在每个不同位置处的随机噪声项影响,则参数估值的协因数阵为:
| $ {\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{\hat x}}}} = \mathit{\boldsymbol{N}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{AN}} $ | (4) |
式中,N的表达式:
| $ \mathit{\boldsymbol{N}} = {\left[ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{A}} - \sigma _2^2\left[ {\begin{array}{*{20}{c}} {\bf{0}}&{\bf{0}}\\ {\bf{0}}&\mathit{\boldsymbol{I}} \end{array}} \right]} \right]^{ - 1}} $ | (5) |
得到所有AP的两个模型参数后,就能通过在待定点处收集各个AP的信号强度来对其进行定位。定位时的观测方程为:
| $ \left\{ \begin{array}{l} {({x_1} - x)^2} + {({y_1} - y)^2} = d_1^2\\ {({x_2} - x)^2} + {({y_2} - y)^2} = d_2^2\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ldots \\ {({x_t} - x)^2} + {({y_t} - y)^2} = d_t^2 \end{array} \right. $ | (6) |
式中,(x1, y1)、(x2, y2)、…、(xt, yt)分别为t个AP的已知坐标;(x, y)为待定点的坐标;d1、d2、…、dt分别为t个AP与待定位点之间的距离,由式(1)通过已算得的模型参数和接收到的信号强度大小得到,表达式为:
| $ {d_i} = {10^{\frac{{{R_0}({d_0}) - R\left( d \right)}}{{10n}}}} $ | (7) |
由于式(6)为关于x、y的非线性方程,故需要先对其线性化,把第2式直至第t式分别减去第1式,得到t-1个关于x、y的线性化方程。将其用矩阵形式表示为:
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{e}} $ | (8) |
式中,y为线性化后的观测向量;A为常系数矩阵;e为观测误差向量。在观测向量中,误差的来源是信号发射端AP与待定点之间的距离,而距离是通过式(7)算得的,它与各个AP的路径衰减因子、1 m处信号强度大小这两个参数的精度有关。对式(7)进行线性化为:
| $ {\rm{d}}d = {\mathit{\boldsymbol{M}}_1}{\rm{d}}({R_0}({d_0})) + {\mathit{\boldsymbol{M}}_2}{\rm{d}}n $ | (9) |
则距离的协因数为:
| $ {\mathit{\boldsymbol{Q}}_d} = \left[ {{\mathit{\boldsymbol{M}}_1}\;\;\;{\mathit{\boldsymbol{M}}_2}} \right]{\mathit{\boldsymbol{Q}}_{\mathit{\boldsymbol{\hat x}}}}\left[ \begin{array}{l} {\mathit{\boldsymbol{M}}_1}\\ {\mathit{\boldsymbol{M}}_2} \end{array} \right] $ | (10) |
式中,
| $ \mathit{\boldsymbol{x}} = {({\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{PA}})^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Py}} $ | (11) |
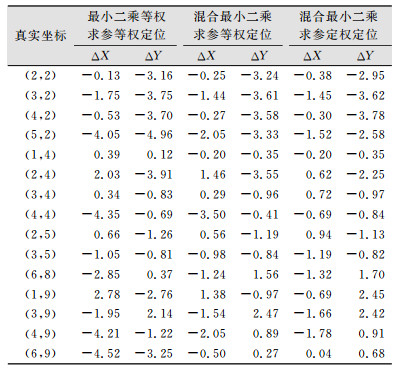
在同济大学体育馆停车场的某处场地进行上述算法的实验,实验场地内共布设有5个AP。求解每个AP的路径衰减因子与1 m处信号强度大小时使用最小二乘法与混合最小二乘法,按式(3)定权来分别处理;在计算待定点坐标时分别按等权、式(11)的方式来定权,最后得到40个测试点的定位结果。部分如表 1所示,表中ΔX、ΔY分别为真实坐标与解算结果的差值。
| 表 1 传统对数路径损耗模型与改进距离模型算法的定位结果对比/m Tab.1 Comparison of Location Results Between Traditional Logarithmic Path Loss Model and Improved Distance Model Algorithm/m |
 |
分析比较时,计算X和Y坐标的中误差[11]为:
| $ {M_X} = \sqrt {\frac{{\sum\limits_{j = 1}^S {\Delta X_j^2} }}{S}} ;{M_Y} = \sqrt {\frac{{\sum\limits_{j = 1}^S {\Delta Y_j^2} }}{S}} $ | (12) |
统计得到,使用最小二乘法等权求对数路径损耗模型中的两个模型参数并等权求待定点坐标,X坐标的中误差为2.279 m,Y坐标的中误差为2.200 m,点位中误差为3.168 m;使用混合最小二乘法按式(3)定权求模型参数,等权求解待定点坐标得到X坐标的中误差为1.342 m,Y坐标的中误差为1.754 m,点位中误差为2.209 m;使用混合最小二乘法按式(3)定权求模型参数,式(11)定权求解待定点坐标得到X坐标的中误差为1.129 m,Y坐标的中误差为1.667 m,点位中误差为2.013 m。
4 结束语本文设计了基于混合最小二乘的AP信号特征定权的改进对数路径损耗模型定位算法,给出了相应的改进公式。利用测试数据,拟合了适合当前室内环境的对数路径损耗模型的参数,建立测距信号强度与距离的关系模型,并按式(11)定权求解待定点坐标。对40个点的实测WiFi定位数据进行了分析,点位精度从3.168 m提高到2.013 m,表明本文的改进算法能得到更好的定位结果。
| [1] |
孙瑜, 范志平. 射频识别技术及其在室内定位中的应用[J]. 计算机应用, 2005, 25(5): 1205-1208. |
| [2] |
申静涛. 于RSSI的对数距离路径损耗模型研究[J]. 电子质量, 2013(12): 15-17. DOI:10.3969/j.issn.1003-0107.2013.12.004 |
| [3] |
薛卫星, 邱卫宁, 花向红, 等. RSSI信号特征值对WiFi室内定位精度的影响分析[J]. 测绘地理信息, 2016, 41(4): 23-26. |
| [4] |
林玮, 陈传峰. 基于RSSI的无线传感器网络三角形质心定位算法[J]. 现代电子技术, 2009, 32(2): 180-182. DOI:10.3969/j.issn.1004-373X.2009.02.054 |
| [5] |
陈岭, 许晓龙, 杨清, 等. 基于三次样条插值的无线信号强度衰减模型[J]. 浙江大学学报, 2011, 45(9): 1521-1538. DOI:10.3785/j.issn.1008-973X.2011.09.003 |
| [6] |
田孝华, 周义建. 无线电定位理论与技术[M]. 北京: 国防工业出版社, 1993.
|
| [7] |
郑卜松, 朱燕飞. 基于RFID室内算法的研究[J]. 电子世界, 2017(23): 23-24. |
| [8] |
肖莉.基于路径损耗的WiFi室内定位系统[D].西安: 西安电子科技大学, 2017
|
| [9] |
毕京学, 甄杰, 郭英. 室内定位无线接收信号强度测距模型的研究[J]. 导航定位学报, 2014, 2(4): 8-10. DOI:10.3969/j.issn.2095-4999.2014.04.002 |
| [10] |
李桢, 黄劲松. 基于RSSI抗差滤波的WiFi定位[J]. 武汉大学学报·信息科学版, 2016, 41(3): 361-366. |
| [11] |
朱律, 沈云中. WiFi室内距离交会定位位置的迭代解法[J]. 测绘地理信息, 2017, 42(4): 58-60. |
 2019, Vol. 44
2019, Vol. 44

