| GPS/GLONASS/BDS/Galileo动态精密单点定位精度及收敛时间分析 | [PDF全文] |
2. 玉溪市不动产登记中心,云南 玉溪,653108;
3. 云南省地震局,云南 昆明,650224
2. Yuxi Real Estate Registration Center, Yuxi 653108, China;
3. Yunnan Earthquake Agency, Kunming 650224, China
自美国GPS(global positioning system)正式运行以来,全球卫星导航系统迅猛发展。目前,GPS和俄罗斯格洛纳斯卫星定位系统(global navigation satellite system,GLONASS)已经具备完全运行能力,欧盟的伽利略卫星定位系统(Galileo positioning system,Galileo)还在不断推进,中国的北斗卫星导航定位系统(BeiDou navigation satellite system,BDS)也于2012年12月27日向亚太区域提供服务。全球卫星导航系统(global navigation satellite system,GNSS)各系统兼容、互操作与数据融合处理成为导航定位领域主要发展趋势之一。
精密单点定位(precise point position,PPP)技术因其只采用单台接收机就能获得高精度定位结果而成为近年来的研究热点,现已被广泛应用于低轨卫星精密定轨、气象、授时、地壳监测等科学研究及工程应用领域。但是PPP技术仍存在一些不足,如收敛时间长,遮挡情况下可视卫星数少影响可靠性及可用性等。已有的研究表明,通过对PPP模糊度固定可加速PPP的收敛[1-4]。另外,多GNSS系统组合PPP可以有效地改善定位精度和收敛时间[5-7]。因为相比单GPS系统,联合处理多卫星系统数据将会显著增强观测几何强度,引入多余观测信息。随着各大卫星导航系统加速建设以及多系统精密轨道和钟差产品精度提高,利用多GNSS联合PPP来提高定位性能也趋于成熟。
本文对4系统动态PPP定位性能进行了分析,主要关注在定位精度和收敛时间。首先,介绍了4系统联合数据处理算法和策略;然后,详细分析了多GNSS联合动态PPP对定位精度和收敛时间的影响;最后,探讨了不同高度角下不同GNSS组合的定位性能表现。
1 GNSS PPP模型与数据处理策略PPP算法中一般采用消电离层组合消除一阶电离层的影响,其伪距和载波观测方程可以表示为:
| $ \left\{ \begin{array}{l} {P_i^s} = {\rho ^s} + c{\rm{d}}{t^s} - c{\rm{d}}t + {m^s}T + {b_{s, i}} - {b_i^s}\\ {L_i^s} = {\rho ^s} + c{\rm{d}}{t^s} - c{\rm{d}}t + {m^s}T + {\lambda _{s, i}}{N_i^s} \end{array} \right. $ | (1) |
式中,Pis、Lis分别为卫星S的消电离层伪距和相位观测值;ρs为测站到卫星之间的几何距离;c为光速;dt为接收机钟差;dts为卫星钟差;bs, i、bis分别为接收机端和卫星端消电离层组合伪距硬件延迟;ms为对流层湿延迟映射函数;T为对流层天顶湿延迟;λs, i为消电离层组合波长;Nis为消电离层组合模糊度,包含了接收机端和卫星端的相位硬件延迟。为了简化观测方程,式(1)中未给出未模型化误差,如多路径、高阶电离层影响等。
当进行4系统联合数据处理时,必须顾及不同导航系统间时间基准差异以及伪距硬件延迟的特点。GPS、BDS、Galileo采用码分多址技术,同一系统卫星使用相同的频率,因此某一测站观测到的同一系统卫星具有相同的接收机端伪距硬件延迟。不同于此的是GLONASS采用频分多址技术,造成不同频率卫星信号进入接收机内部对应通道,由此造成GLONASS卫星间不同的硬件延迟。需要指出的是国际GNSS服务组织(International Global Navigation Satellite System Service, IGS)提供的钟差产品包含卫星端消电离层组合伪距硬件延迟。4系统联合处理时,一般仅估计1个接收机钟差参数,但必须考虑系统时间基准间差异。对于BDS和Galileo,系统间偏差仅与测站有关,与卫星无关;而对于GLONASS卫星,需要估计的系统间偏差与测站和卫星都相关。
本文使用德国地学研究中心(GFZ)提供的MGEX(multi-GNSS experiment)的多系统精密轨道和钟差产品。采用消电离层组合多系统PPP观测方程来消除1阶电离层延迟的影响,忽略2阶以及以上的电离层影响。估计方法为均方根信息滤波(square root information filter,SRIF)。待估参数包括测站坐标、接收机钟差、天顶对流层延迟、模糊度和系统间偏差。其中,测站坐标和接收机钟差进行单历元估计,对流层湿延迟分量采用随机游走过程模拟,模糊度和系统间偏差作为常数估计。滤波过程中,依据动态模型将前一历元状态向量预测至当前历元。卫星端和接收机端天线相位中心改正使用IGS提供的天线文件IGS08.ATX,需要指出的是目前天线文件中没有提供BDS和Galileo接收机端天线相位中心改正,默认采用GPS改正信息。
2 实验结果及分析 2.1 实验数据由于BDS目前还没有提供全球导航定位服务,实验数据选取MGEX网中亚太地区能同时跟踪GPS、GLONASS、BDS、Galileo的GNSS测站。观测时段为2015-12-12-2015-12-25。图 1给出了所选测站的分布示意图,共5个测站。本文对所选测站进行多系统PPP单历元定位,通过分析定位精度、收敛时间以及不同高度角下的定位表现,评估多系统动态PPP的定位性能。
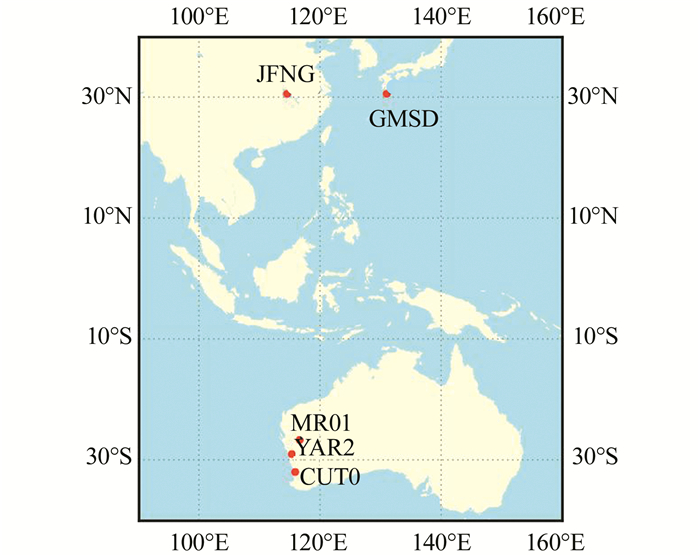 |
| 图 1 测站分布示意图 Fig.1 Distribution of Stations |
2.2 动态定位结果
以2015-12-12 JFNG和MRO1数据为例,进行多系统PPP动态解算,采用G、R、C、G/R、G/R/C、G/R/C/E共6种不同的系统组合模式。图 2为JFNG站4系统天空视图以及测站跟踪各卫星弧段示意图,以颜色标识卫星系统,5颗北斗地球静止轨道(geostationary earth orbits,GEO)卫星全天可视,且均分布在测站的南方,高度角在30°~60°;5颗北斗倾斜地球同步轨道(inclined geosynchronous orbit,IGSO)卫星天空视图呈“∞”,其全天的可视时间可达20 h;北斗地球中轨道(medium earth orbits,MEO)卫星天空视图同其他系统卫星类似。
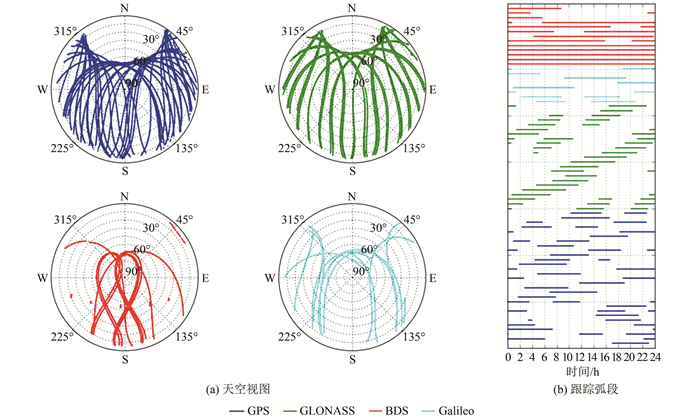 |
| 图 2 2015年DOY 246 JFNG测站天空视图及跟踪弧段 Fig.2 Sky-Plot and Arc of Tracking Data of JFNG on DOY 246 in 2015 |
图 3分别给出了JFNG和MRO1测站多系统组合PPP动态定位误差、卫星数以及几何精度衰减因子(geometric dilution of precision, GDOP)时间序列。为了清楚显示定位初始阶段收敛情况,仅给出了最初2 h的结果。由图 3可知,对于单系统来说,GPS在收敛和精度方面表现最优;BDS收敛时间最长;G/R组合结果相比于单系统,在收敛和精度方面均有明显的改善。对于多系统G/R/C和G/R/C/E,其定位误差基本重叠,表明Galileo的引入对结果的改善并不明显。一方面是因为Galileo卫星个数相对较少;另一方面是因为可视卫星总数较多,导致Galileo观测值对结果的影响进一步降低。此外,观察可视卫星个数和GDOP时间序列可以发现,单BDS可视卫星个数大于单GPS,但是单BDS的GDOP值却大于单GPS的,这一现象表明BDS卫星并没有像GPS卫星一样均匀分布在测站天顶。结合图 1可知,所有的GEO卫星位于赤道上空,相对于测站,大部分观测时段IGSO卫星位于GEO一侧,从而导致绝大多数可视卫星不能均匀的分布于测站天顶。另一个值得注意的是,相比于单GPS以及单GLONASS,单BDS的GDOP值十分平滑,这也是BDS的一个特点,因为可视卫星中近一半卫星为GEO卫星,导致其几何构型变化相对缓慢[8]。相比于单系统,多系统组合极大地降低了GDOP值。多系统组合使得可视卫星数显著增加,GDOP值显著减小,因此在收敛及可靠性上表现更加优异。
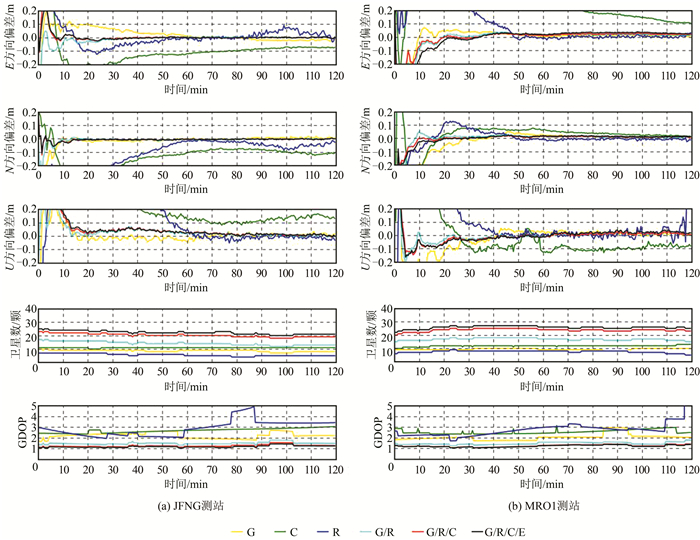 |
| 图 3 2015年第246天多系统组合PPP动态定位误差、卫星数以及GDOP时间序列 Fig.3 Dynamic Positioning Error、Satellite Number and GDOP of Kinematic PPP Combination Solution on DOY 246 in 2015 |
对本文所选的5个测站2015-12-12-2015-12-25的数据进行单GPS和G/R/C/E动态PPP数据处理,其中以静态单天解作为各测站坐标真值,统计各测站收敛时间和定位误差均方根(root mean square,RMS),解算弧段长度以天为单位。需要指出的是收敛标准为平面精度优于0.1 m,高程精度优于0.2 m;定位误差RMS统计的是收敛之后弧段;空白表示观测文件缺失。由图 4可知,除了第346天和第354天,4系统PPP相比于单GPS,精度明显改善;但第346天和第354天4系统PPP的精度远差于单GPS,分析发现:首先,CUT0、MRO1及YAR2在空间位置上十分接近,意味着具有相近的共视卫星;其次,GMSD和JFNG没有出现此问题,并且所选测站的单GPS的定位结果都较好。因此,合理推测是其他系统的精密产品在某些时段精度严重退化导致。总的来说,单GPS PPP在E、N、U方向的平均RMS分别为1.24 cm、0.97 cm、3.59 cm,而4系统PPP在E、N、U方向的平均RMS分别为0.78 cm、0.77 cm、2.48 cm。由图 5可知,4系统联合PPP能有效加速PPP的收敛速度。4系统PPP平均收敛时间为9.8 min,单GPS PPP平均收敛时间为22.7 min。
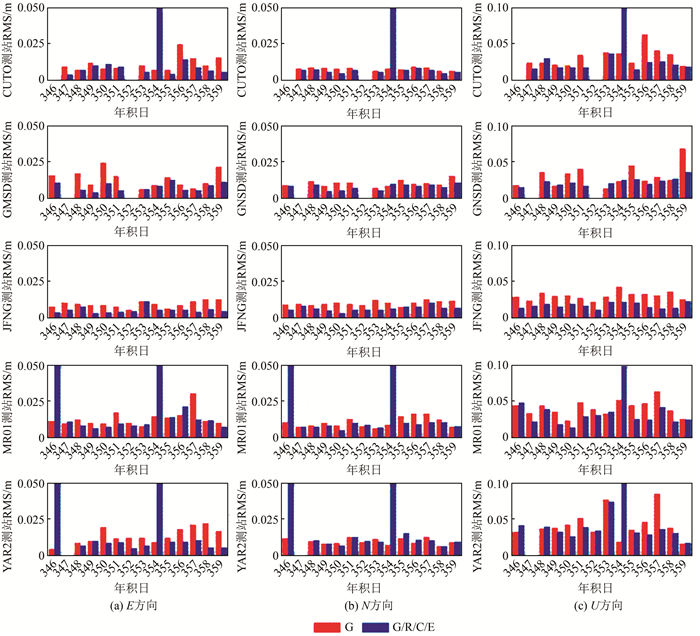 |
| 图 4 单系统及多模组合动态PPP误差RMS统计 Fig.4 RMS Statistics of Positioning Error for Kinematic PPP Solution in GPS and Multi-GNSS Mode |
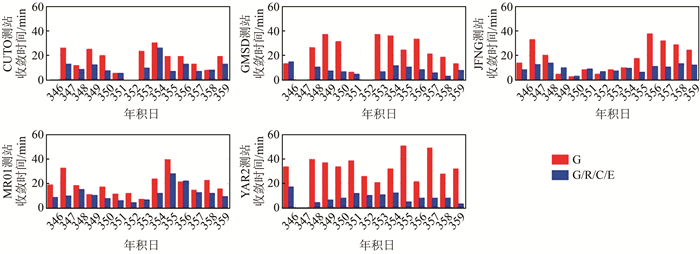 |
| 图 5 单系统及4系统组合动态PPP收敛时间统计 Fig.5 Convergence Time Statistics of Kinematic PPP in GPS and Multi-GNSS Mode |
2.3 截止高度角对定位性能的影响
单系统精密单点定位可用性和可靠性在某些情况下严重削弱,如峡谷地带、城市道路等,因为遮挡,可视卫星数锐减,严重影响定位结果。为了分析单系统和4系统PPP在该场景下定位表现,本文基于不同高度截止角10°~40°进行单GPS和G/R/C/E组合PPP数据处理。图 6为以JFNG测站为例的实验,包括定位结果、可视卫星个数以及GDOP等信息。随着截止高度角增加,可视卫星数逐渐减少,GDOP值逐渐增大。当截止高度角为30°时:单GPS系统的可视卫星数大约5个,而此时4系统的可视卫星数维持在15个左右;单GPS系统GDOP值部分时段超过了10,而4系统GDOP值维持在3的水平;4系统水平定位结果仍同低截止高度角时保持一致,稳定性明显优于单GPS。当截止高度角为40°时:单GPS的可视卫星数已经小于5个,GDOP值大多时段超过10,此时定位误差时间序列抖动剧烈,无法提供精密位置服务;而4系统可视卫星数仍然维持在10个,GDOP值大约为6,其定位结果在水平方向上仍然表现出较好的稳定性,只是在高程方向上稳定性有所降低。因此,多系统联合处理使得测站可视卫星数明显增加,卫星空间几何结构明显优化,有效增强了定位结果的可靠性及可用性。
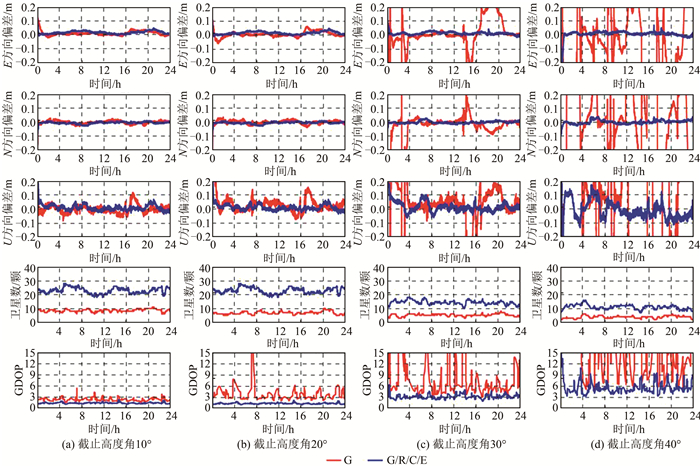 |
| 图 6 2015年DOY 246不同截止高度角下的JFNG测站单系统及4系统组合动态PPP定位误差、卫星个数以及GDOP时间序列 Fig.6 Dynamic Positioning Error、Satellite Number and GDOP of Kinematic PPP Combination Solution of JFNG Station in GPS and Multi-GNSS Mode Under Different Elevation Cutoffs, on DOY 246 in 2015 |
3 结束语
本文基于均方根信息滤波估计方法实现了4系统联合PPP解算。通过对所选MGEX测站实测数据的处理,详细分析了动态多系统组合PPP定位性能,得到结论如下。
1) 与GPS单系统PPP相比,多系统联合PPP在精度及收敛速度上具有明显改善。精度在E、N、U方向分别由1.24 cm、0.97 cm、3.59 cm提高到0.78 cm、0.77 cm、2.48 cm;收敛时间由22.7 min变为9.8 min。
2) 多系统联合PPP使得测站可视卫星数明显增加,卫星空间几何结构明显优化,有效增强了定位结果的可靠性及可用性。
致谢: 感谢MGEX提供的多系统精密轨道和钟差产品以及多系统观测数据。
| [1] |
张小红, 李星星. 非差模糊度整数固定解PPP新方法及实验[J]. 武汉大学学报·信息科学版, 2010, 35(6): 657-660. |
| [2] |
潘宗鹏, 柴洪洲, 刘军, 等. 基于部分整周模糊度固定的非差GPS精密单点定位方法[J]. 测绘学报, 2015, 44(11): 1 210-1 218. |
| [3] |
张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1 399-1 407. |
| [4] |
李盼. GNSS精密单点定位模糊度快速固定技术和方法研究[D].武汉: 武汉大学, 2016 http://cdmd.cnki.com.cn/Article/CDMD-10486-1016113506.htm
|
| [5] |
王进, 杨元喜, 张勤, 等. 多模GNSS融合PPP系统间偏差特性分析[J]. 武汉大学学报·信息科学版, 2019, 44(4): 475-481. |
| [6] |
赵齐乐, 李晓涛, 耿江辉. GPS/GLONASS/BeiDou/Galileo PPP快速模糊度固定[J]. 测绘地理信息, 2018, 43(3): 1-8. |
| [7] |
任晓东, 张柯柯, 李星星, 等. BeiDou、Galileo、GLONASS、GPS多系统融合精密单点[J]. 测绘学报, 2015, 44(12): 1 307-1 313. |
| [8] |
张小红, 左翔, 李盼, 等. BDS/GPS精密单点定位收敛时间与定位精度的比较[J]. 测绘学报, 2015, 44(3): 250-256. |
 2020, Vol. 45
2020, Vol. 45


