| 一种应用K-近邻算法优选点云数据生成格网DEM插值的方法 |
2. 武汉大学灾害监测和防治研究中心, 湖北 武汉, 430079;
3. 佛山市测绘地理信息研究院,广东 佛山, 528000
2. Hazard Monitoring and Prevention Research Center, Wuhan University, Wuhan 430079, China;
3. Foshan Surveying Mapping and Geoinformation Research Institute, Foshan 528000, China
数字高程模型(digital elevation model,DEM)作为GIS空间数据库中最重要的地理信息之一,在国民经济建设、城市规划、灾难预警等方面发挥着越来越重要的作用。随着科技的发展,获取DEM原始数据的手段也有了长足的进步,由各种激光扫描仪获取的点云数据成为DEM重要的原始数据[1, 2],原始数据经过滤波处理,过滤掉非地面点,经过滤波处理后的点云数据通过基于三角网的建模方法、基于格网的建模方法和两者混合的建模方法生成DEM[3, 4]。基于格网的建模方法凭借拓扑关系简单、分析处理算法易于实现以及某些空间操作及存储组织灵活方便成为常用的建模方法之一。在基于格网的建模方法中,利用规则或不规则的原始数据内插生成规则格网,内插方法包括反距离权重插值(inverse distance to a power)、克里金插值(Kriging)和自然邻域插值(natural neighbor)[5-8]等,如果在构建规则格网的时候将这几种插值方法都使用一遍再比较哪种插值方法更合适,无疑是费时费力的。同时,各种插值方法情况不同,效果不一样:克里金插值在平缓地形下表现最好;自然邻域插值在陡峭地形下表现最好;而反距离权重插值抵抗噪声的能力更好,在点云数据很稀疏时表现也较好。考虑到实际工作的复杂性,插值方法需要考虑多种因素影响,因此,本文提出了用K-近邻算法作为技术手段,在实际生产过程中选择合适的点云数据生成格网DEM插值方法,提高了插值的精度和效率。
1 优选点云数据生成格网DEM插值方法利用K-近邻算法优选格网DEM插值方法的基本思想是:首先,构建具有代表性、数据量合适且已经知最优插值方法的地表样本数据库;其次,提取地形点云数据的特征信息,与地表样本数据库中的地表样本进行匹配,从地表样本数据库中找到与实际观测数据最邻近的数据,以获得合适的插值方法。
1.1 地表样本数据库的构建地表样本数据库中的地表样本由两个部分构成,一部分是由对插值方法影响较大的地表样本数据的特征因子组成的特征部分,如地形坡度、点云噪声、点云密度等;另外一部分是地表样本在特征部分对应的标签,即表现最好的插值方法:
| $ \mathit{\boldsymbol{D}}{_i}:{\rm{ }}\left[ {V_i^1\;\;V_i^2\;\; \cdots \;\;V_i^j\;\; \cdots \;\;V_i^n\;\;{\rm{Labe}}{{\rm{l}}_i}} \right] $ | (1) |
式中, Vij指第i个地表样本的第j个特征; Labeli指第i个地表样本表现最好的格网插值方法。衡量的标准为地形点云数据经过插值后形成的DEM模型的均方根误差(root mean square error,RMSE)为:
| $ {\rm{RMSE}} = \frac{{\mathop \sum \limits_{i = 1}^n {{\left( {{E_i} - {T_i}} \right)}^2}}}{n} $ | (2) |
式中,Ei代表某点利用插值方法得到的高程值;Ti代表该点实际的高程值。
构建地表样本数据的详细步骤如下:通过事先确定好的特征因子生成模拟地形的点云数据;利用软件对点云数据分别进行反距离权重插值、克里金插值和自然邻域插值3种插值方法;比较这3种插值方法形成的DEM模型的精度,选择精度最高的插值方法作为标签。
构建地表样本数据库需要m个地表样本数据,根据实际情况确定m,如只考虑一种特征因子的情况下,m=n1;考虑i种特征因子的综合影响下,m=n1×n2×…×ni, n1、n2、…、ni的数值由特征因子的范围和取值间隔确定。
1.2 K-近邻算法优选格网DEM插值方法构建DEM的地形原始点云往往数据量巨大,如果提取地形特征时通过全部的原始点云进行计算,工作量太大,本文通过以下方法得到地形特征:①先随机从海量点云数据中选择20个较小的样本;②计算这20个样本的特征;③取所有样本的特征期望值作为整个海量地形点云数据的特征值构建地形特征向量:
| $ \mathit{\boldsymbol{D}}{_x}:{\rm{ }}\left[ {V_x^1\;\;V_x^2\;\; \cdots \;\;V_x^j\;\; \cdots \;\;V_x^n} \right] $ | (3) |
提取海量地形点云数据的特征后,与地表样本数据库中的样本特征进行匹配,地表样本数据库是已知最优插值方法且具有代表性的实际地形数据特征向量的数据库:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{D}}{_1}:{\rm{ }}\left[ {V_1^1\;\;V_1^2\;\; \cdots \;\;V_1^j\;\; \cdots \;\;V_1^n\;\;{\rm{Labe}}{{\rm{l}}_1}} \right]\\ \mathit{\boldsymbol{D}}{_2}:{\rm{ }}\left[ {V_2^1\;\;V_2^2\;\; \cdots \;\;V_2^j\;\; \cdots \;\;V_2^n\;\;{\rm{Labe}}{{\rm{l}}_2}} \right]\\ \;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ \mathit{\boldsymbol{D}}{_m}:{\rm{ }}\left[ {V_m^1\;\;V_m^2\;\; \cdots \;\;V_m^j\;\; \cdots \;\;V_m^n\;\;{\rm{Labe}}{{\rm{l}}_m}} \right] \end{array} \right. $ | (4) |
式中, D1、D2、…、D m∈ R m×n为地表样本的特征所组成的向量; Labeli为第i个地表样本最合适的格网插值方法。
匹配采用的距离度量方式为欧氏距离:
| $ {\rm{dis}}{{\rm{t}}_i} = {\left\| {{\mathit{\boldsymbol{D}}_i} - {\rm{ }}{\mathit{\boldsymbol{D}}_x}} \right\|_2} $ | (5) |
获取m个地表样本向量与观测数据向量的欧氏距离后,进行排序,选取K个与观测向量欧氏距离最小的地表样本数据,获取这些地表样本数据的Label,统计标签个数,个数最多的标签即为观测数据最合适的格网插值方法。具体流程为:从地形点云数据中提取地形点云数据特征,与地表样本数据库进行特征匹配,选择k个最匹配的地表样本中出现次数最多的插值方法,得出地形最合适的插值方法。
2 实验及结果分析考察应用K-近邻算法优选点云数据生成格网DEM插值方法的有效性:首先,本文的实验部分分析了对插值方法影响较大的地表样本数据的特征因子(地形坡度和点云噪声率,其中,点云噪声率指噪声点占点云数据中全部点的百分比)对不同插值方法的影响;其次,构建了地形坡度和点云噪声率为特征因子的地表样本数据库;最后,利用实测数据对应用K-近邻算法优选点云数据生成格网DEM插值方法的有效性进行了检验。
2.1 不同坡度和噪声对3种插值方法影响分析 2.1.1 单一特征因子对插值方法影响为分析单一特征因子对插值方法的影响,在只存在单一特征因子的情况下进行了多次插值,得到的RMSE结果如表 1和表 2所示。
| 表 1 点云噪声率作为单一特征因子的各插值方法RMSE/m Tab.1 RMSE of Each Interpolation Method of Point Cloud Noise Rate as a Single Feature Factor/m |
 |
| 表 2 坡度作为单一特征因子的各插值方法RMSE/m Tab.2 RMSE of Each Interpolation Method of Slope as a Single Feature Factor/m |
 |
将表 1和表 2中的数据利用可视化工具得到单一特征因子对各插值方法RMSE影响的折线图如图 1所示。
 |
| 图 1 点云噪声率或坡率作为单一特征因子各插值方法的RMSE折线图 Fig.1 RMSE Polyline of Each Interpolation Method of Point Cloud Noise Rate or Slope as a Single Feature Factor |
从图 2可以看出,当点云噪声率作为单一特征因子时,随着噪声率的增大,各种插值方法对应的RMSE值也在增大;当坡度作为单一特征因子时,随着坡度的增大,各种插值方法对应的RMSE值也会增大(因为量级相差较大,40°前的情况不能从图中反映出来;Kri与NaN的曲线重叠度较高)。
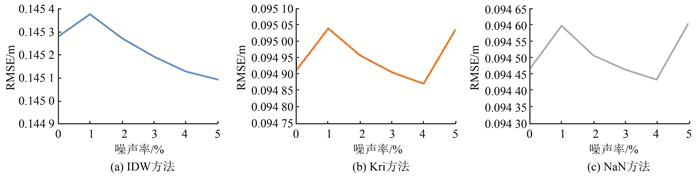 |
| 图 2 坡度为70°时噪声的变化导致不同插值方法构建的DEM模型的RMSE变化折线 Fig.2 Slope Is 70 °, Change of Noise Leads to the RMSE Polyline of DEM Model Constructed by Different Interpolation Methods |
2.1.2 多个特征因子对插值方法的影响
在只存在一个特征因子的情况下,通过图 1可以看出,RMSE和特征因子呈正相关。在两个特征因子同时存在(坡度为70°且点云噪声率(0~5%))的情况下,本文通过插值得到的RMSE结果,如表 3所示,数据的可视化如图 2所示。
| 表 3 两个特征因子都存在时各插值方法RMSE/m Tab.3 RMSE of Each Interpolation Method Under Existion for both Feature Factors/m |
 |
从图 2可以看出,当坡度为70°时,噪声的变化与RMSE的变化不是正相关的。因此,当两种特征因子一起存在的情况下,RMSE与特征因子的关系可能是非线性的。
从各个插值方法在不同条件下的RMSE值可以看出,不同插值方法受特征因子的影响不同,图 3是利用ArcGIS生成的栅格图,从图 3中可以更直观地观察到不同的插值方法受坡度、噪声的影响大小。在坡度变化区域可以看出,IDW表现最差,最不平滑,NaN表现最好;在噪声存在的区域可以看到,IDW将噪声控制得最好。
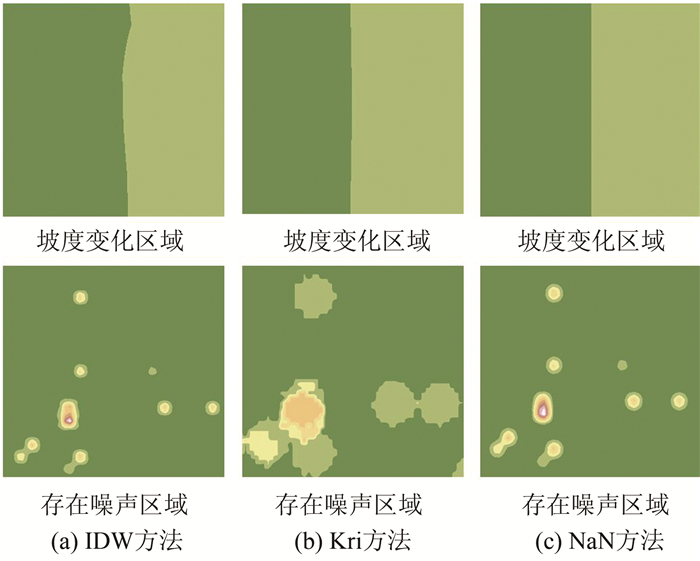 |
| 图 3 不同插值方法对噪声和坡度的抵抗力 Fig.3 Resistance to Noise and Slope of Different Interpolation Methods |
2.2 K-NN算法优选DEM插值方法结果分析 2.2.1 利用K-NN算法优选DEM插值方法
本文选取坡度和噪声率作为特征因子,坡度为0°、10°、20°、30°、40°、50°、60°、70°时,n1=8;测量噪声大小在10 cm内随机分布,噪声率为0、1%、2%、3%、4%、5%时,n2=6,总计生成m=n1×n2=48个地表样本数据来模拟实际地形,构建地表样本数据库。
利用RIGEL VZ-1000扫描的实地数据来验证方法的正确性。选取坡度较为平缓的草坪和坡度较陡的山坡作为扫描地区。利用前文提到的提取地形特征的方法,获取扫描地区的特征信息如下:草坪地区高程差为0.06 m,平均坡度为5.0°,点云噪声率为1%;山坡地区高程差为2.722 m,平均坡度为18.7°,点云噪声率为4%。图 4是扫描地区的等高线图,图中等高线均以0.01 m为间隔。
 |
| 图 4 测试地区的等高线图 Fig.4 Contour Map of the Test Area |
已知扫描地区的点云数据特征,按照前文提到的方法编写程序,输入特征通过程序匹配地表样本数据库中合适数目的地表样本,从而获取扫描地区最合适的插值方法。在平面地区,Kri是最佳构建DEM的插值方法;在坡地区,NaN是最佳构建DEM的插值方法。
2.2.2 利用ArcGIS进行结果验证利用ArcGIS软件中的插值功能对两个扫描地区进行插值,通过程序分析,得到平面地区和坡地区各插值方法构建的DEM的插值精度,如表 4所示。
| 表 4 扫描地区插值结果/m Tab.4 Interpolation Result of Scaning Area/m |
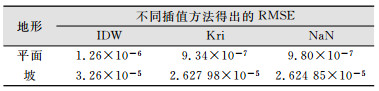 |
从表 4中可以看到,在平面地区,Kri精度最好,与利用本文提出的优选DEM插值方法的结果一致;NaN在坡地区表现最好,与利用本文提出的优选DEM插值方法的结果也相同。证明利用K-NN算法优选DEM插值方法具有一定的可行性。
3 结束语本文选取地形坡度和点云噪声率作为特征因子,将K-NN算法应用到选择合适的DEM插值方法中,并设计实验进行了验证。实验结果表明,本文提出的方法快速有效,提高了基于格网的建模方法的插值速度和精度。除了本文提到的地形复杂程度和点云噪声率之外,影响插值方法的特征因子还有很多,需要在今后的研究中进一步完善。
| [1] |
潘少奇, 田丰. 三维激光扫描提取DEM的地形及流域特征研究[J]. 水土保持研究, 2009, 16(6): 102-105. |
| [2] |
拓万兵, 吴凤民. 利用MATLAB实现DEM可视化方法研究[J]. 测绘地理信息, 2017, 42(4): 32-34. |
| [3] |
余红举, 吴晨曜, 周军元, 等. 多源数据生产DEM方法探索[J]. 测绘地理信息, 2016, 41(6): 86-88. |
| [4] |
李瑞宗, 杨诚, 李柏延. 一种高精度数字高程模型生成的新方法[J]. 导航定位学报, 2014, 2(3): 80-82. DOI:10.3969/j.issn.2095-4999.2014.03.017 |
| [5] |
马翔, 黄要武. 几种常用高程插值方法的比较[J]. 江西测绘, 2012(1): 51-53. |
| [6] |
周兴华, 姚艺强, 赵吉先. DEM内插方法与精度评定[J]. 测绘科学, 2005, 30(5): 86-88. DOI:10.3771/j.issn.1009-2307.2005.05.031 |
| [7] |
Shahbeik S, Afzal P, Moarefvand P, et al. Comparison Between Ordinary Kriging (OK) and Inverse Distance Weighted (IDW) Based on Estimation Error. Case Study: Dardevey Iron Ore Deposit, NE Iran[J]. Arabian Journal of Geosciences, 2014, 7(9): 3 693-3 704. DOI:10.1007/s12517-013-0978-2 |
| [8] |
胡杰. 基于规则格网的DEM建模方法研究[J]. 测绘与空间地理信息, 2012, 35(11): 138-140. DOI:10.3969/j.issn.1672-5867.2012.11.044 |
 2019, Vol. 44
2019, Vol. 44


