| 一种结合均值和互信息的线上AP选取新算法 |
2. 武汉大学测绘学院, 湖北 武汉, 430079;
3. 武汉大学灾害监测与防治研究中心,湖北 武汉, 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China
近年来,室内定位技术[1, 2]由于其广泛的应用前景逐渐成为一个研究热点。随着北斗系统的加入,GNSS(global navigation satellite system)由于其高精度、全天候的特性成为室外定位导航的主流技术手段[3, 4]。然而,由于室内环境的遮挡和多径效应,GNSS在室内定位的应用受到了较大的局限。如何实现低成本、低功耗、高精度的定位是室内定位面临的主要问题。基于RSS(received signal strength)的WiFi室内定位技术具有成本低、部署简单易行的特性[5],目前其定位精度一般约为3~5 m,考虑到AP选取对WiFi位置估计算法的影响,如何更快、更好地选取观测质量较好的AP是提高WiFi室内定位精度的一个关键因素。
实际观测中往往存在大量的冗余AP,冗余AP会增加位置估计的计算量和内存空间,观测质量过差的AP甚至会严重损害位置估计的精度[6]。从N个AP选取M个AP用于位置估计可以将位置估计的计算量从N维空间降至M维空间,从而减少计算时间,同时通过剔除观测质量较差的AP能够有效提升WiFi位置估计的性能。基于位置指纹的WiFi室内定位算法主要分为两个阶段:线下指纹库建立阶段和线上位置估计阶段[7]。目前已有的AP选取算法按照其执行的阶段可以分为线下AP选取算法和线上AP选取算法两大类。线下AP选取算法能够利用更多的指纹点观测信息,因此,选取的AP能够更加充分地表征指纹点的特征。线上阶段AP选取算法则注重于反映环境的动态变化,在变化复杂的环境中更加适用。文献[8]提出了一种基于最大均值的AP选取策略,该算法选取RSS均值最大的AP作为观测质量较好的AP进行位置估计,计算简单、高效,然而其不能反映AP携带的信息量以及AP间的相互干扰。文献[9]提出了一种基于线上互信息的AP选取策略,该算法通过最小化AP子集的互信息使得AP子集的信息量更大,且减少了AP间的相关性,然而当观测区域可观测的AP较多时,该算法定位阶段的运行时耗较大,且容易受到观测质量过差的AP的影响,其鲁棒性较差。结合上面两种算法的优势,本文提出了一种结合均值和互信息的线上AP选取新算法,并利用贝叶斯位置估计算法[10-12]对其进行了性能评估。
1 线上AP选取新算法本文提出的线上AP选取算法主要有以下两个步骤:
1) 基于均值最大的AP初步选取。初步选取阶段,选取RSS均值较大的AP作为精确选取的初始AP子集。初步选取能够减少精确选取阶段AP的数量,同时剔除观测质量过差的AP。
2) 基于互信息最小化的AP精确选取。该阶段从初始AP子集中选取出指定个数的互信息最小的AP子集用于位置估计,通过最小化AP子集的互信息,能够有效地减少AP子集的信息冗余,降低其相关性。
1.1 最大均值的AP初选取室内环境随时间变化的特性使得AP的RSS观测值存在抖动现象,部分观测质量过差的AP甚至会出现大量的信号丢失。均值最大的AP选取策略认为AP的观测信号强度越强,其观测质量越好,受到环境动态变化的影响更小,更加有利于位置估计。假定某个测试点观测了N个AP的k个历元的观测数据,则基于均值最大的AP选取算法主要分为以下两步:
1) 依次计算各个AP的k个历元观测数据的均值,记为RSSi, i=1, 2, …, N。公式为:
| $ {\overline {{\rm{RSS}}} _i} = \frac{1}{k}\sum\limits_{j = 1}^k {{\rm{RSS}}_i^j}, i = 1, 2, \cdots, N $ | (1) |
式中,RSSij表示第i个AP的第j个历元的RSS观测值。
2) 对N个AP按照均值从大到小的顺序进行降序排列,选取出前M个均值最大的AP作为初步选取的AP子集。
从上述基于均值最大的AP选取算法原理可以看出,其仅仅考虑单个AP自身的观测特征,然而当室内存在多个AP时,该算法无法顾及AP相互间存在的干扰现象。
1.2 互信息最小化的AP精选取为了进一步提升WiFi位置估计的性能,本文通过最小化AP间的互信息,从而降低最终选取的AP子集的信息冗余和相关性。基于互信息最小化的AP选取算法基本原理如下:对于初步选取的M个AP进行两两组合,分别计算各个组合的互信息,找出互信息最小的组合作为初始AP,记为AP1、AP2。公式为:
| $ MI({\rm{A}}{{\rm{P}}_i}, {\rm{A}}{{\rm{P}}_j}) = H({\rm{A}}{{\rm{P}}_i}) + H({\rm{A}}{{\rm{P}}_j})-H({\rm{A}}{{\rm{P}}_i}, {\rm{A}}{{\rm{P}}_j}) $ | (2) |
式中,MI(APi, APj)表示APi和APj的互信息;H(APi)和H(APj)分别表示APi和APj的信息熵;H(APi, APj)表示APi和APj的联合信息熵。
分别计算余下的M-2个AP与AP1、AP2组合的互信息,公式为:
| $ MI({\rm{A}}{{\rm{P}}_1}, {\rm{A}}{{\rm{P}}_2}, {\rm{A}}{{\rm{P}}_i}) = H({\rm{A}}{{\rm{P}}_1}, {\rm{A}}{{\rm{P}}_2}) + H({\rm{A}}{{\rm{P}}_i})-H({\rm{A}}{{\rm{P}}_1}, {\rm{A}}{{\rm{P}}_2}, {\rm{A}}{{\rm{P}}_i}) $ | (3) |
式中,MI(AP1, AP2, APi)表示APi与AP1、AP2组合的互信息。找出使得MI(AP1, AP2, APi)最小的AP作为第3个AP,并且记为AP3,则AP3满足
依次选取出下一个最优的AP,直到最优AP的个数达到指定的AP个数为止。第L个最优AP的选取公式如下:
| $ \begin{gathered} MI({\rm{A}}{{\rm{P}}_1}, {\rm{A}}{{\rm{P}}_2}, ..., {\rm{A}}{{\rm{P}}_L}) = \hfill \\ H({\rm{A}}{{\rm{P}}_1}, {\rm{A}}{{\rm{P}}_2}, ..., {\rm{A}}{{\rm{P}}_{L-1}}) + H({\rm{A}}{{\rm{P}}_L})-\hfill \\ H({\rm{A}}{{\rm{P}}_1}, {\rm{A}}{{\rm{P}}_2}, ..., {\rm{A}}{{\rm{P}}_L}) \hfill \\ \end{gathered} $ | (4) |
为了考虑动态环境下AP选取结果对WiFi位置估计精度的影响,本文利用贝叶斯位置估计策略对新算法进行了实例分析。贝叶斯后验估计的基本原理如下:
| $ p\left( {{L_i}|{\rm{RSS}}} \right) = \frac{{p\left( {{\rm{RSS}}|{L_i}} \right)p\left( {{L_i}} \right)}}{{p\left( {{\rm{RSS}}} \right)}} $ | (5) |
式中,RSS表示选取的AP在位置估计点的RSS观测向量;p(Li|RSS)表示观测到RSS向量后,观测者位于位置Li的条件概率,即观测向量RSS出现在位置Li的概率;p(RSS|Li)表示在给定位置Li观测到给定RSS的条件概率,可采用直方图统计的方法计算;p(Li)表示位置Li的概率,通常不考虑指纹点之间的差异,即指纹点等概率;p(RSS)表示RSS出现的全概率,假定AP之间相互独立,其计算公式如下:
| $ \begin{gathered} p({\rm{RSS}}) = \hfill \\ p({\rm{RS}}{{\rm{S}}_1})p({\rm{RS}}{{\rm{S}}_2}) \cdots p({\rm{RS}}{{\rm{S}}_T}) = \prod\limits_{i = 1}^T {p({\rm{RS}}{{\rm{S}}_i})} \hfill \\ \end{gathered} $ | (6) |
式中,p(RSSi)表示第i个AP观测值的离散概率。
将全概率计算公式(6)回代至贝叶斯后验估计式(5),可以得到后验条件概率。利用多个指纹点的贝叶斯加权位置估计公式可以快速解算出位置估计点的坐标,即
| $ \begin{gathered} (x, y) = \sum\limits_{i = 1}^K {{w_i} \times ({x_i}, {y_i})} = \hfill \\ \sum\limits_{i = 1}^K {\frac{{p({\rm{RSS}}|{L_i})p({L_i})}}{{p({\rm{RSS}})}} \times ({x_i}, {y_i})} \hfill \\ \end{gathered} $ | (7) |
式中,(x, y)表示位置估计点的坐标;(xi, yi)表示第i个指纹点的坐标;wi表示第i个指纹点的权重,即贝叶斯后验条件概率;K表示邻近点个数。
采用平均定位误差(mean square error, MSE)评估新算法的位置估计精度,MSE的计算公式如下:
| $ {\rm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{\delta _i}} $ | (8) |
式中,n表示测试点的个数;δi表示测试点的点位误差,其计算公式如下:
| $ {\delta _i} = \sqrt {{{({x_i}-x_i^{{\rm{real}}})}^2} + {{({y_i}-y_i^{{\rm{real}}})}^2}} $ | (9) |
式中,(xi, yi)表示第i个测试点的估计位置坐标;(xireal, yireal)表示第i个测试点的真实坐标。
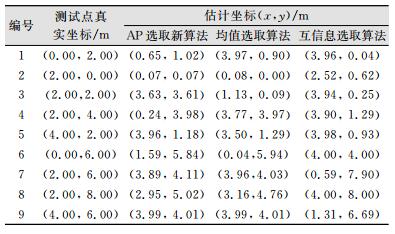
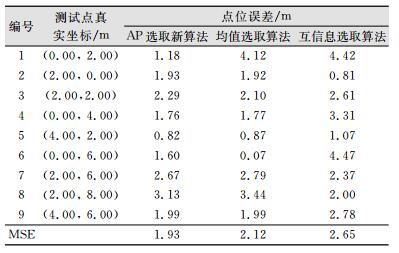
3 实验与结果分析为了测试线上AP选取新算法的性能,选取其学生机房进行了实际场景的分析。实验中以小米手机作为AP信号接收器持续观测RSS信号,数据采样率为1 Hz,由于硬件时延和信号丢失,实际采样率约小于1 Hz。实验共选取了6个指纹点和9个测试点,每个点上均持续观测3 min,并记录所有可观测到的AP观测值,部分观测质量较差的AP观测历元不足50%。实验方案如图 1所示,图 1中,□表示测试点,●表示指纹点,其坐标系采用独立坐标系。表 1、表 2给出了3种不同AP选取算法的位置估计坐标结果及精度统计结果,其中,均值AP选取算法表示基于均值最大的AP选取算法,互信息AP选取算法表示基于互信息最小的AP选取算法。从表 2可以看出, 新方法的点位误差最差为3.13 m,基于均值选取算法的点位误差最差为4.12 m,基于互信息选取算法的点位误差最大为4.47 m,并且编号为1和6的点位误差均超过4 m,其定位结果较差。同时线上选取新算法的MSE为1.93 m,明显小于基于均值最大的AP选取算法和基于互信息最小的AP选取算法,因此新算法相比两种AP单独选取算法具有更高的位置估计精度。其原因可能是基于均值最大的AP选取策略无法排除AP间相互干扰的情况,而基于互信息最小化的AP选取策略无法对单个AP自身观测质量的好坏进行很好的区分,因此会引入观测质量较差的AP, 从而引起定位精度的降低。表 3给出了3种不同算法的AP选取耗时。
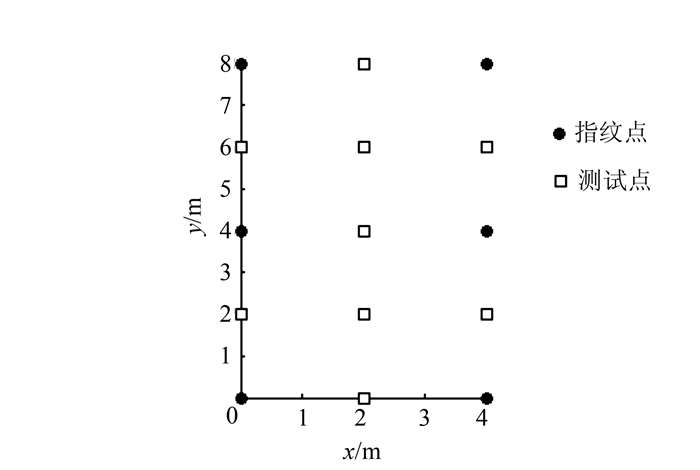 |
| 图 1 实验方案分布图 Figure 1 Experimental Plan Distribution |
| 表 1 不同AP选取算法的位置估计坐标 Table 1 Position Estimation Coordinates of Different AP Selection Algorithms |
 |
| 表 2 不同AP选取算法的位置估计精度 Table 2 Location Estimation Accuracy of Different AP Selection Algorithms |
 |
| 表 3 AP选取算法耗时 Table 3 Time Cost of AP Selection Algorithm |
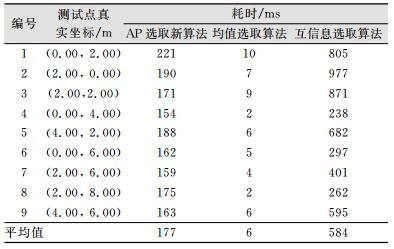 |
从表 3可以看出,结合均值和互信息的AP选取算法时间消耗相比基于互信息最小化的AP选取策略时间大量减少,平均耗时约为其1/3,但是新算法和基于互信息的AP选取算法耗时明显高于基于均值最大的AP选取算法,其主要是由于互信息的计算过程复杂而导致的大量运算引起的,两种方法的平均计算时间分别约为其31倍和101倍。因此, 新算法需要在耗时上进行进一步的改进, 减少线上阶段位置估计的时延,从而进一步提升用户体验。
4 结束语本文对基于位置指纹的WiFi室内定位技术进行了探讨,并深入研究了其中AP选取算法对位置估计的性能影响。针对室内环境动态变化的特性,综合考虑均值最大AP选取策略以及互信息最小的AP选取策略的优势,提出了一种新的线上AP选取策略。通过分步选取AP的形式提高WiFi位置估计的精度,并且在一定程度上降低了时间消耗。新算法利用均值最大对AP进行初步选取,达到剔除观测质量过差的AP以及降低互信息最小化AP选取搜索空间维度的目的; 接着利用互信息最小化选取策略实现AP的精确选取,达到降低AP信息冗余和相关性的目的。实验分析表明,新算法相比单独基于互信息最小化的AP选取策略和单独基于均值最大的AP选取策略具有更高的位置估计精度,其耗时相比基于互信息最小化的AP选取也有较大的降低,然而相比基于均值最大的AP选取策略, 其时间消耗引起的位置估计时延依然较为明显。线下阶段的大量信息的利用将在进一步的研究工作中展开,以期进一步改进WiFi位置估计系统的性能。
| [1] | 赵锐, 钟榜, 朱祖礼, 等. 室内定位技术及应用综述[J]. 电子科技, 2014, 27(3): 154–157 |
| [2] | 朱庆, 熊庆, 赵君峤. 室内位置信息模型与智能位置服务[J]. 测绘地理信息, 2014, 39(5): 1–7 |
| [3] | 张清华, 王源, 孙阳阳, 等. 北斗卫星导航系统空间信号可用性的初步评估[J]. 测绘地理信息, 2015, 40(6): 22–24 |
| [4] | 李征航. GPS测量与数据处理[M]. 2版. 武汉: 武汉大学出版社, 2005 |
| [5] | 刘春燕, 王坚. 基于几何聚类指纹库的约束KNN室内定位模型[J]. 武汉大学学报·信息科学版, 2014, 39(11): 1 287–1 292 |
| [6] | Eisa S, Peixoto J, Meneses F, et al. Removing Useless APs and Fingerprints from WiFi Indoor Positioning Radio Maps[C]. International Conference on Indoor Positioning and Indoor Navigation 2013 (IPIN2013), Montbeliard, France, 2013 |
| [7] | Kim Y, Shin H, Chon Y, et al. Smartphone-based WiFi Tracking System Exploiting the RSS Peak to Overcome the RSS Variance Problem[J]. Pervasive & Mobile Computing, 2013, 9(3): 406–420 |
| [8] | Youssef M A, Agrawala A, Shankar A U. WLAN Location Determination via Clustering and Probability Distributions[C]. IEEE International Conference on Pervasive Computing and Communications, Fort Worth, Texas, America, 2003 |
| [9] | Zou H, Luo Y, Lu X, et al. A Mutual Information Based Online Access Point Selection Strategy for WiFi Indoor Localization[C]. 2015 IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 2015 |
| [10] | 徐元坤. 基于WiFi和Android平台的室内定位技术研究[J]. 测绘地理信息, 2015, 40(6): 21–24 |
| [11] | Roos T, Myllymäki P, Tirri H, et al. A Probabilistic Approach to WLAN User Location Estimation[J]. International Journal of Wireless Information Networks, 2002, 9(3): 155–164 DOI: 10.1023/A:1016003126882 |
| [12] | 宣伟, 花向红, 邹进贵. 抛物面天线表面的拟合检测方法研究[J]. 测绘地理信息, 2015, 40(3): 34–37 |
 2018, Vol. 43
2018, Vol. 43

