| 两种对流层延迟修正模型的比较与分析 |
对流层导致的GPS信号传播路径增长的距离即为对流层延迟量,天顶方向的对流层延迟约为2.3 m;而卫星高度角为10°时,对流层延迟将增加至13 m左右[1]。对流层为非弥散介质,不能用双频观测值来消除对流层延迟[2]。在GPS数据处理中,一般采用对流层延迟模型对GPS观测数据进行修正[3]。这种方法只能消除大部分对流层延迟的影响,延迟残差仍然能够对GPS定位精度产生较大的影响。目前,大部分解算GPS基线的随机软件都采用了建立对流层延迟模型的处理方式。
本文在微软基础类(microsoft foundation classes, MFC)框架下,编程实现了Hopfield模型和Saastamoinen模型,在得出模型值的基础上,计算出不同高度角对应的模型值以及模型间的差值。
1 对流层延迟模1) Hopfield模型。温度T、气压P、水汽压e以及高程h的关系为:
| $\left\{ \begin{align} & \frac{\text{d}T}{\text{d}h}=-6.8{}^\circ /\text{km} \\ & \frac{\text{d}P}{\text{d}h}=-\rho g \\ & \frac{\text{d}e}{\text{d}h}=-\rho g \\ \end{align} \right.$ | (1) |
可以看出,高程h每增加1 km, 气温T就下降6.8 ℃,直至对流层的外边缘气温等于绝对温度0 ℃时为止;气压P和水汽压e也随着高度h的增加而降低,其变化率与大气密度ρ和重力加速度g有关。顾及气态方程,可导出Hopfield模型为:
| $\left\{ \begin{align} & \Delta S=\Delta {{S}_{d}}+\Delta {{S}_{w}}=\frac{{{K}_{d}}}{\sin {{\left( {{E}^{2}}+6.25 \right)}^{\frac{1}{2}}}}+ \\ & \frac{{{K}_{w}}}{\sin {{\left( {{E}^{2}}+2.25 \right)}^{\frac{1}{2}}}} \\ & {{K}_{d}}=155.2\times {{10}^{-7}}\cdot \frac{{{P}_{s}}}{{{T}_{s}}}\left( {{h}_{d}}-{{h}_{s}} \right) \\ & {{K}_{w}}=155.2\times {{10}^{-7}}\cdot \frac{4810}{T_{s}^{2}}{{e}_{s}}\left( {{h}_{w}}-{{h}_{s}} \right) \\ & {{h}_{d}}=40136+148.72\left( {{T}_{s}}-273.16 \right) \\ & {{h}_{w}}=11000 \\ \end{align} \right.$ | (2) |
式中,温度均采用绝对温度,以(°)为单位;气压P和水汽压e均以mbar为单位;高度角E以(°)为单位;ΔS、ΔSd、ΔSw均以m为单位;hs为观测站的高程。
2) Saastamoinen模型。除Hopfield模型外,Saastamoinen[4-7]模型也是一种应用广泛的模型,在许多GPS数据处理的软件中得到应用。有研究证明,在高海拔地区,Saastamoinen模型对对流层延迟的模拟效果要比Hopfield模型更好。推导Saastamoinen模型为:
| $\begin{gathered} \Delta S = \frac{{0.002277}}{{\sin E}}\left[ {{P_s} + \left( {\frac{{1255}}{{{T_s}}} + 0.05} \right){e_s} - \frac{B}{{{{\tan }^2}E}}} \right] \cdot \hfill \\ W\left( {\varphi \cdot H} \right) + \delta R \hfill \\ \end{gathered} $ | (3) |
式中,W(φ·H)=1+0.002 6cos2φ+0.000 28hs,其中,φ为观测站的纬度; B是hs的列表函数; δR为E和hs的列表函数。
经过数值拟合后,式(3)可转化为:
| $\left\{ \begin{align} & \Delta S=\frac{0.002277}{\sin {{E}_{s}}}\left[ {{P}_{s}}+\left( \frac{1255}{{{T}_{s}}}+0.05 \right){{e}_{s}}-\frac{{{a}_{s}}}{{{\tan }^{2}}{{E}_{s}}} \right] \\ & {{E}_{s}}=E+\Delta E \\ & \Delta E=\frac{16"}{{{T}_{s}}}\left( {{P}_{s}}+\frac{4810}{{{T}_{s}}}{{e}_{s}} \right)\cot E \\ & {{a}_{s}}=1.16-0.15\times {{10}^{-3}}{{h}_{s}}+0.716\times {{10}^{-8}}{{h}_{s}}^{2} \\ \end{align} \right.$ | (4) |
式中,符号含义与Hopfield模型相同。
2 湿气压的确定和数据准备计算对流层延迟模型值,需要用到湿气压值。可以利用CDDIS提供的气象数据文件中的气温T、气压P、相对湿度HR等气象数据来计算湿气压e[8, 9],计算公式为:
| $e = {H_R} \times {e^{\left( { - 37.2465 + 0.213166 \times T - 0.000256908 \times {T^2}} \right)}}$ | (5) |
然后,根据湿气压值计算对流层延迟的模型值。
IGS服务组织可以提供全球范围内多种格式的观测数据。本文采用IGS站BJFS的观测数据。BJFS观测站位于北京市境内,观测数据可从CDDIS网站下载。本文的研究用到的数据有:①气象观测数据(*.m格式,用于计算对流层延迟模型值);②精密星历(*.sp3格式,结合BJFS站坐标计算高度角);③精确对流层延迟值(*.zpd格式,作为参考值与延迟模型值对比)。
3 算法实现与分析本文在MFC框架下, 利用C++语言对Hopfield模型和Saastamoinen模型进行了实现。由于CDDIS提供的数据都是文本文件,数据存储有着严格的定义,所以,在读取文本数据时,需要严格按位读取,存放到事先定义的结构体中。
通过程序分别计算出Hopfield模型和Saastamoinen模型对应的延迟值,并和IGS提供的对流层延迟参考值一起以折线图表示,结果如图 1所示。
在图 1中,竖轴表示天顶方向对流层延迟值,精确到1 mm;横轴表示观测时间,单位是h。从图 1可以看出,Hopfield模型和Saastamoinen模型的模型值相差很小,在几个mm以内。而两种模型和IGS提供的.zpd格式的对流层延迟参考值差值的量级在cm级。
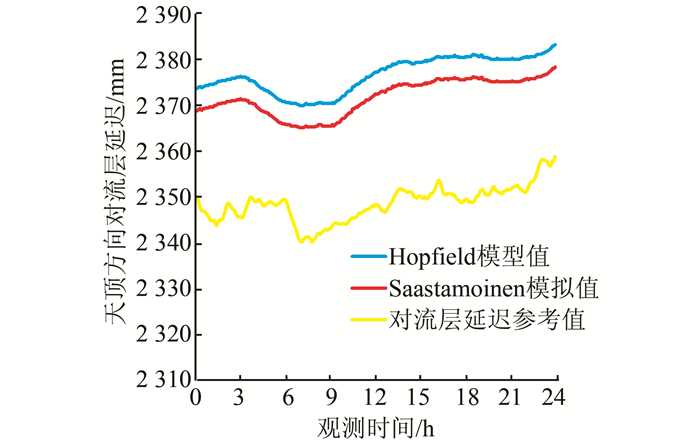 |
| 图 1 两种模型值和对流层延迟参考值随时间变化图 Figure 1 Diagram of Two Model Values and the Tropospheric Delay Reference Value Changes over Time |
根据模型值和对流层延迟参考值,相互求差计算,结果如图 2所示。
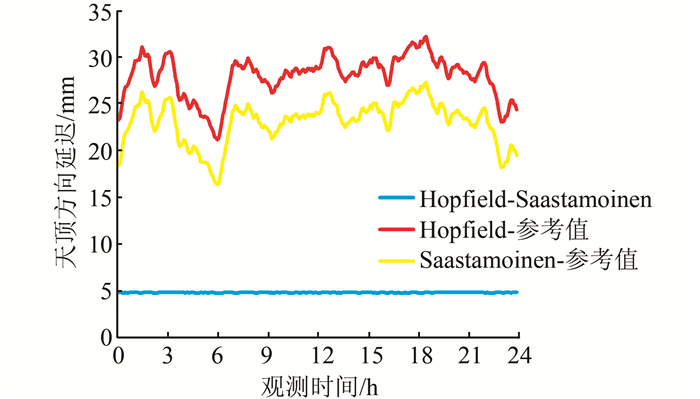 |
| 图 2 模型间及模型与参考值的差值随时间变化图 Figure 2 Diagram of Difference Between the Models and the Models with the Reference Value Changes over Time |
从图 2可以看出,Hopfield模型和Saastamoinen模型的差值稳定在5 mm左右,Hopfield模型与对流层延迟参考值的差值稳定在20~25 mm之间,Saastamoinen模型和参考值之间的差值稳定在25~30 mm之间。由此可见,两种模型对对流层延迟模拟的效果较好,模型差值的量级稳定在mm级。
笔者根据*.SP3格式的精密星历文件和BJFS站的坐标计算卫星高度角,并在程序中筛选出高度角大于10°的部分,以折线图的形式输出,结果如图 3所示。
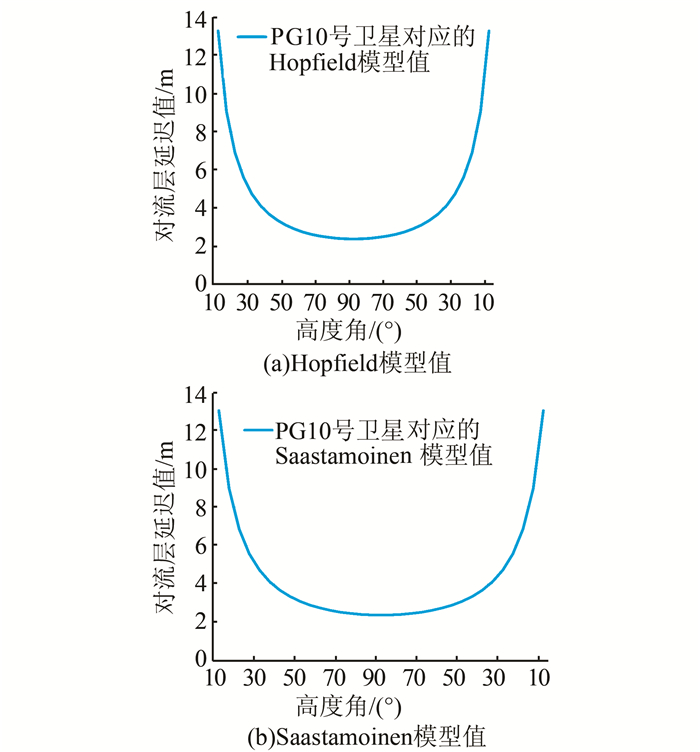 |
| 图 3 不同高度角时PG10号卫星的对流层延迟模型值 Figure 3 Troposphere Delay Model Values of PG10 at Different Altitude Angles |
从图 3得出,两种模型的延迟值随高度角的减小而增大。当卫星高度角为90°时,对流层延迟值最小,约为2.3 m;当卫星高度角减小时,对流层延迟值逐渐增大,增大速率也逐渐加快;当高度角减小到10°时,对流层延迟值达到13 m左右。
笔者在前面工作的基础上,通过模型间求差,进一步计算出PG10号卫星不同高度角时的模型差值,结果如图 4所示。
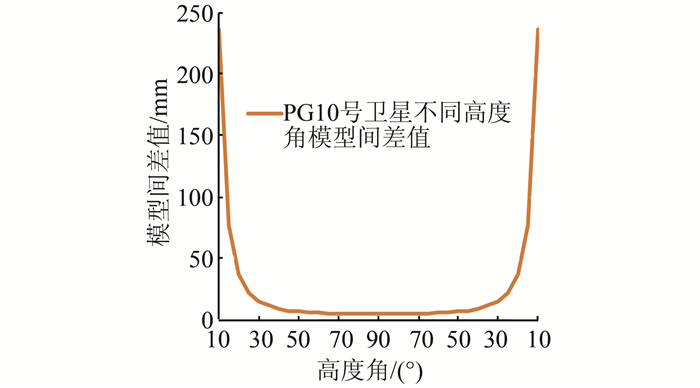 |
| 图 4 PG10号卫星不同高度角时的模型间差值 Figure 4 Difference Between the Models of PG10 at Different Altitude Angles |
从图 4可以看出,当卫星高度角为90°时,模型间差值最小,约为5 mm; 当卫星高度角减小时,模型间差值逐渐增大,增大速率也逐渐加快;当高度角减小到10°时,模型间差值达到24 cm左右,模型之间的差异逐渐显著。模型对对流层模拟的效果变差。因此,根据测站情况,设置合适的高度角十分必要。
4 结束语通过对Hopfield模型和Saastamoinen模型进行程序实现,结合IGS提供的对流层延迟参考值,并进行分析比较,得出如下结论。
1) Hopfield模型、Saastamoinen模型以及参考值在天顶方向随时间变化的趋势相同。
2) 天顶方向的对流层延迟约2.3 m,对于一般的工程实践,会产生很大的影响。因此,消除对流层延迟的影响显得格外重要。
3) 天顶方向的Hopfield模型和Saastamoinen模型之间的差值稳定在5 mm左右,两种模型与参考值之间的差值稳定在2~3 cm。模型间、模型与参考值间的差值的量级较小。两种模型之间能够较好的吻合,能够消除绝大部分对流层延迟的影响。
4) 两种模型的延迟值随高度角的减小而增大。随着高度角的减小,对流层延迟快速增大,即使用改正模型消除了大部分误差的影响,但残差的量级仍足以影响观测数据的可用性。
| [1] |
欧吉坤. GPS测量的中性大气折射改正的研究[J].
测绘学报,1998,27(1) : 31–36.
Ou Jikun. Research on the Correction for the Neutral Atmospheric Delay in GPS Surveying[J]. Acta Geodaetica et Cartographica Sinica,1998,27(1) : 31–36. |
| [2] |
张勤, 李家权.
GPS测量原理及应用[M]. 北京: 科学出版社, 2005 .
Zhang Qin, Li Jiaquan. GPS Measurement Principle and Application[M]. Beijing: Science Press, 2005 . |
| [3] |
李昭, 邱卫宁, 邱蕾, 等. 几种对流层延迟改正模型的分析与比较[J].
测绘通报,2009,(7) : 16–18.
Li Zhao, Qiu Weining, Qiu Lei, et al. Some Tropospheric Delay Correction Models: Analysis and Comparison[J]. Bulletin of Surveying and Mapping,2009,(7) : 16–18. |
| [4] |
李征航, 黄劲松.
GPS测量与数据处理[M]. 武汉: 武汉大学出版社, 2005 .
Li Zhenghang, Huang Jinsong. GPS Surveying and Data Processing[M]. Wuhan: Wuhan University Press, 2005 . |
| [5] |
徐绍铨, 张华海, 杨志强.
GPS测量原理及应用[M]. 武汉: 武汉大学出版社, 2001 .
Xu Shaoquan, Zhang Huahai, Yang Zhiqiang. GPS Measurement Principle and Application[M]. Wuhan: Wuhan University Press, 2001 . |
| [6] |
任亚飞, 柯熙政. GPS定位误差中对流层延迟的分析[J].
西安理工大学学报,2006,22(4) : 407–410.
Ren Yafei, Ke Xizheng. An Analysis of Troposphere Delay in GPS Positioning Error[J]. Journal of Xi'an University of Technology,2006,22(4) : 407–410. |
| [7] |
王新龙, 李亚峰. GPS定位中4种对流层延迟修正模型适应性分析[J].
电光与控制,2008,15(11) : 5–9.
Wang Xinlong, Li Yafeng. Applicability Analysis of Four Sorts of Troposphere Delay Error Models in GPS Positioning[J]. Electronics Optics and Control,2008,15(11) : 5–9. |
| [8] |
丁金才.
GPS气象学及其应用[M]. 北京: 气象出版社, 2009 .
Ding Jincai. GPS and Its Application in Meteorology[M]. Beijing: China Meteorological Press, 2009 . |
| [9] |
刘大杰, 施一民, 郭静瑶.
全球定位系统的原理与数据处理[M]. 上海: 同济大学出版社, 2003 .
Liu Dajie, Shi Yimin, Guo Jingyao. Principle of Global Positioning System and Data Processing[M]. Shanghai: Tongji University Press, 2003 . |
 2016, Vol. 41
2016, Vol. 41


