| 川滇地区垂向GPS时间序列共模误差提取与分析 |
随着全球导航卫星系统(global navigation sa-tellite system,GNSS)技术的发展和观测质量的不断提高,GNSS已广泛应用于大地测量与地球动力学研究[1-3]。很多国家和地区都建立了全球框架下的区域全球定位系统(global positioning system, GPS)观测网络,如中国大陆构造环境监测网络(crustal movement observation network of China, CMONOC)。针对区域GPS观测网络的研究中发现,各GPS站点的时间序列存在空间相关的误差,称为共模误差(common mode error,CME)。CME的提取能提高GPS序列的信噪比[4]。针对CME,很多学者提出了不同的方法进行CME的提取,如堆栈方法[5]、PCA(principal component analysis)方法[6]、KLE(Karhunen-Loeve Expansion)方法[7]等,其中,PCA是CME提取中最常用的方法。通常情况下,在GPS时间序列分析中,CME被当做误差进行去除,但研究表明,CME除了与空间相关的误差外,还包含很多有用的信息[8]。本文利用PCA方法对川滇地区GPS观测网络1 000 d的垂向序列数据进行共模成分的提取,并结合影响地壳周期形变的主要因素非构造形变对GPS观测网络中的共模周期成分进行了对比分析。
1 PCA原理与时空滤波主成分分析是在某种准则下,通过将多元观测变量以线性变化的形式投影变换为多个不相关的变量。在GPS观测网络中,n个测站的GPS时间序列阵为X (i, j),其协方差矩阵为B,B为n阶对称矩阵,B可以分解为:
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{V \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{V}}^{\rm{T}}} $ | (1) |
式中,V为n阶正交特征向量矩阵;Λ为由k个特征值组成的非零对角矩阵。X由正交函数基V表示为:
| $ \mathit{\boldsymbol{X}} = \mathit{\boldsymbol{AV}} $ | (2) |
式中, A为m×n阶矩阵。则GPS观测网中,CME的共模误差ε表示为:
| $ \varepsilon = \sum\limits_{k = 1}^p {{a_k}{v_{jk}}} $ | (3) |
式中,ak为第k个主成分;vjk为第k个主成分对X的空间响应。一般情况下,第一个主成分对应的空间响应为共模的,即解释为GPS时间序列的CME。
此外,在对角阵Λ中,特征值大小可以表示对应的主成分对协方差阵的贡献大小。所对应的特征值越大,则对应的主成分对原始序列的贡献率越大,一般前几个主成分就可以包含原始序列的绝大部分信息。
2 川滇地区实例分析本文对CMONOC在川滇地区的GPS网络40余个站点的垂向时间序列进行了分析。川滇地区为中国构造运动最强烈的地区之一,发育多条断裂带,地震发生频繁。因此,利用大地测量资料对该地区进行相关研究具有重要意义。本文研究的相关站点分布如图 1所示。
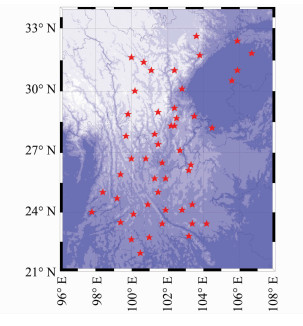 |
| 图 1 川滇地区GPS站点分布图 Figure 1 Distribution of GPS Stations in Sichuan-Yunnan Region |
本文选取的数据是CMONOC网络公布的GPS垂向时间序列,数据采用GAMIT/GLOCK联合解算完成,最终结果为在全球参考框架ITRF2008下的单天原始坐标序列。在时空滤波前,对川滇地区GPS站数据进行数据预处理。选取了数据较为完整的42个测站垂向序列1 000 d的数据,对数据进行粗差探测和去除,缺失数据进行插值补缺,同时更正了由于更换天线或地震活动引起的时间序列中的阶跃项。文献[8]指出,在小区域内,整个GPS监测网也有周期性变化特点,因此在本文PCA滤波中没有去除周期项。采用PCA对42个站点序列进行时空分析,前3个主成分如图 2所示。
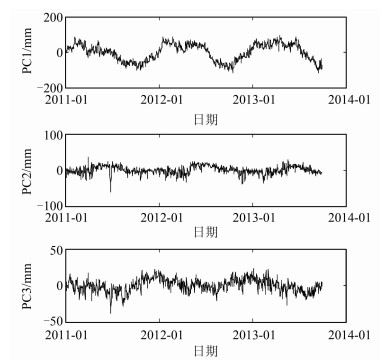 |
| 图 2 PCA时空滤波中的前3个主成分 Figure 2 The First Three Principal Components in PCA Spatiotemporal Filtering |
根据PCA原理,第一个主成分贡献率达到了68.9%,且其对应的空间响应分布相似,笔者将其表示为川滇地区GPS网络的共模成分。判断了共模部分后,根据式(3)可以计算川滇地区GPS站点的CME,进一步从各站点序列中减去CME,提高GPS观测序列的信噪比。经过CME改正后,GPS时间序列的平均均方根值从8.83 mm减小为4.93 mm,减少了44%。从图 2中可以看到,共模部分具有明显的年周期性。为了更好地对其进行分析,笔者对PC1进行了频谱分析,如图 3所示,结果明显呈现了PC1中的年周期项。
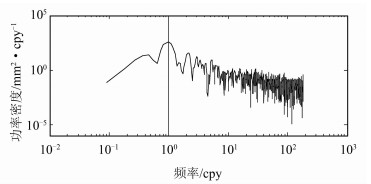 |
| 图 3 PC1频谱分析结果 Figure 3 Spectrum Analysis Result of PC1 |
3 质量负荷改正与分析
在GPS观测序列中,通常包含了非构造形变的信息[9]。对GPS序列进行非构造形变信息的分析与改正能进一步提高利用GPS序列研究地壳形变的精度。非构造形变一般包括潮汐形变和地表质量负荷变化引起的形变。其中,在CMONOC站点时间序列解算中,潮汐形变(包括海潮、极潮及固体潮模型)已用目前建立的较为精确的改正模型做了相应改正,固体潮和极潮采用IERS2003模型,海潮采用FES2004模型。质量负荷变化主要包括大气负荷、非潮汐海洋负荷、积雪和土壤水负荷。已有的分析表明,GPS时间序列中的年周期与半年周期性信号主要由地表质量负荷变化所引起[10, 11]。
一些研究表明,在中国大陆地区,主要受大气负荷和土壤水负荷的影响。质量负荷利用国际上公布的大气或土壤水的全球格网模型负荷格林函数计算。笔者利用QOCA软件计算了川滇地区各GPS站点的大气负荷与土壤水负荷,其中气压数据和土壤水数据均采用美国国家环境预报中心提供的全球格网数据。气压数据时间分辨率为6 h,空间分辨率为2.5°×2.5°;土壤水数据时间分辨率为24 h,空间分辨率为1.75°×1.75°。为了与GPS时间序列相对应,最终计算的负荷值均归算为分辨率为1 d的数据。各站点所计算得到的平均值如图 4所示。
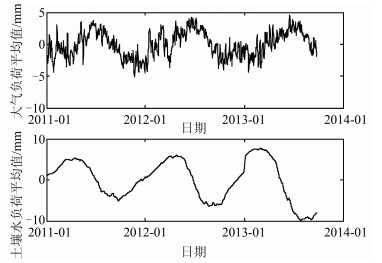 |
| 图 4 川滇地区GPS站点大气负荷与土壤水负荷平均值 Figure 4 Mean Values of Deformation Caused by Atmospheric and Soil Moisture of GPS Stations |
从图 4可以看出,大气负荷和土壤水负荷引起的地壳形变十分显著,且具有明显的年周期性。大气负荷变化引起的地表形变可以达到5 mm左右,而土壤水负荷变化引起的地表形变达到了近10 mm。袁林果等[8]针对香港地区基准站的研究表明,GPS时间序列中的CME成分主要由地表质量负荷变化所引起,因此,笔者将川滇地区计算的负荷改正平均值从平均的CME(PC1乘以对应的空间响应)中去除,再对去除质量负荷改正后的序列做频谱分析,结果如图 5所示。图 5中实线为改正前,虚线为改正后,表明GPS的CME在进行地表质量负荷改正后年周期性明显减小。
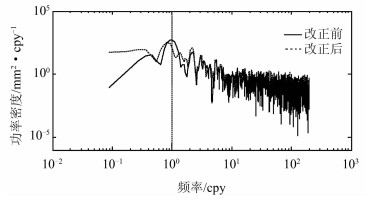 |
| 图 5 共模误差进行质量负荷改正前后频谱分析结果 Figure 5 Spectrum Analysis Result of CME Before and After Mass Loading Correction |
4 结束语
本文利用PCA对陆态网川滇地区GPS时间序列进行了CME的提取与分析。经过PCA时空滤波后,GPS坐标序列的均方根值减少了44%。并进一步计算了川滇地区地表质量负荷变化引起的位移形变,通过频谱分析分析了CME与地表质量负荷改正的关系。结果表明,PCA滤波可以有效去除川滇地区垂向GPS时间序列的CME,提高GPS时间序列的信噪比;地表质量负荷变化可以解释垂向GPS时间序列CME中的年周期变化特征。
| [1] | Segall P, Davis J L. GPS Applications for Geodynamics and Earthquake Studies[J]. Annual Review of Earth and Planetary Sciences, 1997, 25(6): 301–336 |
| [2] | 杨业, 谢益炳, 陆亚峰, 等. 基于陆态网数据低阶球谐函数电离层区域建模[J]. 测绘地理信息, 2015, 40(3): 45–47 |
| [3] | Dong D, Fang P, Bock Y, et al. Anatomy of Appa-rent Seasonal Variations from GPS-Derived Site Position Time Series[J]. Journal of Geophysical Research: Solid Earth, 2002, 107(B4): 1–16 |
| [4] | Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3): 1–16 |
| [5] | Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Positions for Estimating Coseismic and Postseismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth, 1997, 102(B8): 18 257–18 070 |
| [6] | 殷海涛, 甘卫军, 熊永良, 等. PCA空间滤波在高频GPS定位中的应用研究[J]. 武汉大学学报·信息科学版, 2011, 36(7): 825–829 |
| [7] | 贺小星, 花向红, 周世健, 等. PCA与KLE相结合的区域GPS网坐标序列分析[J]. 测绘科学, 2014, 39(7): 113–117 |
| [8] | 袁林果, 丁晓利, 陈武, 等. 香港GPS基准站坐标序列特征分析[J]. 地球物理学报, 2008, 51(5): 1 372–1 384 |
| [9] | 王敏, 沈正康, 董大南. 非构造形变对GPS连续站位置时间序列的影响和修正[J]. 地球物理学报, 2005, 48(5): 1 045–1 052 |
| [10] | 姜卫平, 李昭, 刘鸿飞, 等. 中国区域IGS基准站坐标时间序列非线性变化的成因分析[J]. 地球物理学报, 2013, 56(7): 2 228–2 237 |
| [11] | 彭葳, 戴吾蛟. 基于EEMD和Husrt指数的GNSS基准站的垂向速率估计[J]. 测绘工程, 2016, 25(4): 60–65 |
 2018, Vol. 43
2018, Vol. 43

