| 顾及速度约束的基于时间序列GPS漂移数据处理方法 |
在GPS相对定位中,观测值的主要误差来源包括大气延迟、多路径效应以及衍射等。多路径效应广泛存在于各类复杂环境中,特别是高楼林立的城市地区存在城市峡谷效应:高层建筑和树木等都会成为反射物,干扰卫星信号的接收[1]。衍射误差是GPS信号经过障碍物体边缘时,直射信号发生弯曲而产生的多余路径[2]。另外,金属物体 (如避雷针、金属支架或电力线) 对GPS信号也会产生较大影响[3]。上述误差的存在将严重损害GPS定位的精度,造成GPS轨迹数据漂移,从而大大降低用户交通方式判别和出行规律挖掘的准确性。
目前,GPS精度评定和校正漂移数据的方法主要包括基于精度衰减因子DOP (dilution of precision) 的方法[4]、基于高程的算法和基于时间序列的算法3种。文献[5]中提出一种基于通视卫星数量和位置精度因子PDOP (position dilution of precision) 的算法,将PDOP值大于4或者为0的定位点和通视卫星数量小于4的定位点视为不可靠的点,并将其去除。这个方法能够有效去除系统误差,但是一般纯GPS位置采样设备难以获取相关卫星数据。文献[6]中基于高程的算法是利用漂移点在高程上的突变来判定噪声。文献[7]中使用WiFi辅助下附有高程信息的GPS定位,将测区的平均大地高作为先验的高程信息,这在高差变化不大的城市区域是可以接受的。然而,对于地形起伏较大的区域,比如本文中测试的兴趣区域——武汉大学周边地区,这两种基于高程的算法可能在高程变化较大的地方产生误判。文献[8-11]中描述的基于时间序列的算法是一种较为通用的算法,它用单位根检测方法DF (Dickey-Fuller) 对经 (纬) 度-时间序列的自相关函数进行稳定性检验,来分析一段轨迹是否存在漂移,再通过自相关系数的异常推出漂移点。然而,当一条轨迹上点数较多时,DF方法对少量的漂移点不敏感。而且,通过自相关系数来判断漂移点的方法并不直观。本文提出的基于时间序列的改进算法先根据每个点的拐角进行轨迹分段,在每一段中利用更精确的单位根检测方法ADF (Augmented Dickey-Fuller)[12]进行自相关分析。再根据速度-时间序列的方差和均值判断漂移点。与传统的时间序列法相比,这种方法能够更敏感、更精准地求出漂移点。
1 轨迹漂移和数据来源 1.1 GPS轨迹漂移在定位过程中,导航电文一个主帧需要30 s才能播发完毕,而地面接收机往往需要1 min左右的时间才能完成定位[13]。根据本小组的实地观测,在天气较好并且较空旷的场所,在Garmin fēnix GPS手表上开启GPS后需要1~2 min的时间来进行卫星搜索和定位,从室内或者其他信号不好的地方刚刚走出时也需要一定的时间来重新定位。因此首点和信号较差的地方往往会出现漂移点,在本文的实验中,漂移点的纬度、经度差在0.000 3°以上,距离可达几十至上百米。漂移点情况如图 1所示,图中深色线段为轨迹,并用虚线圈将漂移点标出。
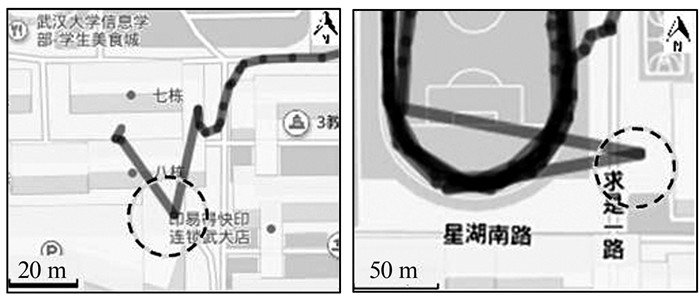 |
| 图 1 GPS轨迹漂移 Figure 1 Data Drift in GPS Trajectories |
这些漂移点的出现会对轨迹的分析结果造成很大的影响,因此对这些漂移点的检测和修正也十分必要。
1.2 数据来源本文实验数据来源于23名武汉大学学生志愿者。每位志愿者佩戴一块Garmin fēnix GPS腕表,在武汉大学及周边地区进行了为期6个月的出行轨迹数据采集,收集到共计697条轨迹,其中志愿者愿意公开且质量优良的有效轨迹为413条。
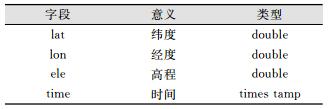
GPS腕表获取的轨迹文件格式为.gpx,其中包括一条轨迹上每个采样点的经度、纬度、高程、时间和整条轨迹的总移动距离、总时间、平均速度等信息。为便于介绍,将涉及的变量定义如表 1所示。
| 表 1 GPS原始数据格式 Table 1 Format of GPS Raw Data |
 |
2 轨迹漂移处理 2.1 算法思路
本文采用的处理方法是先根据轨迹点的拐角特性将轨迹分段[14],对分段后的轨迹段逐一进行自相关系数的检查, 判断是否存在漂移点。对检查出存在漂移点的轨迹段利用每个点的速度属性进行判断,找出具体的漂移点,最后对这些漂移点进行样条插值处理来进行修正。思路流程图如图 2所示。
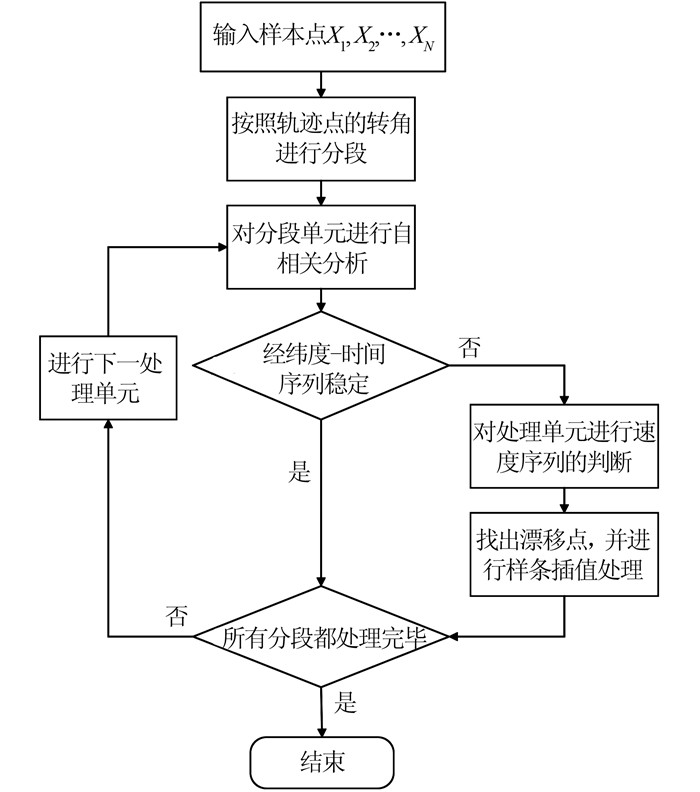 |
| 图 2 思路流程图 Figure 2 Flow Chart of Data Drift Processing Method |
2.2 处理过程
处理过程分以下4个步骤。
2.2.1 轨迹分段1) 计算每个点的夹角以及拐角。如图 3所示,a为第i-1个采样点和第i个采样点之间的距离,b为第i个采样点和第i+1个采样点之间的距离,c为第i-1个采样点和第i+1个采样点之间的距离。
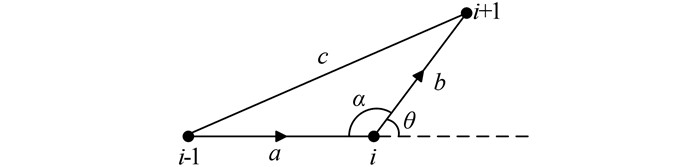 |
| 图 3 拐点示意图 Figure 3 Turning Point in A Trajectory |
第i个点的夹角α为:
| $ \alpha = {\rm{ar}}\cos (\frac{{{a^2} + {b^2} + {c^2}}}{{2ab}}) $ |
第i个点的转角θ为:
θ=π-α
2) 设定一个阈值ω,对每一个点的拐角进行判断,若|θ|>ω,则将该点标记为拐点。
3) 对标记的拐点进行抽稀处理,将处理后的每两个拐点之间的数据作为一段处理单元。为了防止拐点正好是漂移点的情况,将每段数据向前和向后扩展3~5个轨迹点。
考虑到可能存在走走停停的情况,因此在分段后需要对每一段序列进行局部的自相关系数检测处理,根据空间位置的相关性来找出存在漂移点的序列。
2.2.2 局部自相关系数检测1) 对§2.2.1中得到的每一个处理单元,计算它的经度自相关系数序列,利用ADF方法对自相关系数序列进行检测,若证明原序列为稳定序列,则继续对其纬度序列进行相同处理。
2) 若证明其中一个序列为不稳定序列,就认为该序列存在漂移,进入下一步骤。
2.2.3 基于速度约束的漂移点判定1) 计算处理单元序列中每个点的速度vi
| $ {v_i} = \frac{a}{{{t_i}-{t_{i-1}}}} $ |
2) 对速度序列计算出它的均值μ以及方差σ。
3) 对每个点的速度进行判断,若 (vi-μ)2>3σ,并且vi>μ,则该点是一个漂移点。
2.2.4 对漂移点进行样条插值处理1) 对§2.2.3中找到的漂移点进行如下判断:①若两个漂移点相邻,则只处理第一个点; ②若前后没有漂移点,则处理该点。
2) 对应处理的点在轨迹序列中找到它前面的3个采样点,分别对经度和纬度进行样条插值处理,处理结果替换掉该点的原始经纬度。
3) 对处理后的序列进行验证处理。重复上述步骤1~2次。
3 实验结果与讨论 3.1 实验过程在对已经采集到的武汉大学学生日常轨迹数据进行筛选后,选择了几条在地图上能明显看出存在漂移的轨迹数据,如图 4所示。
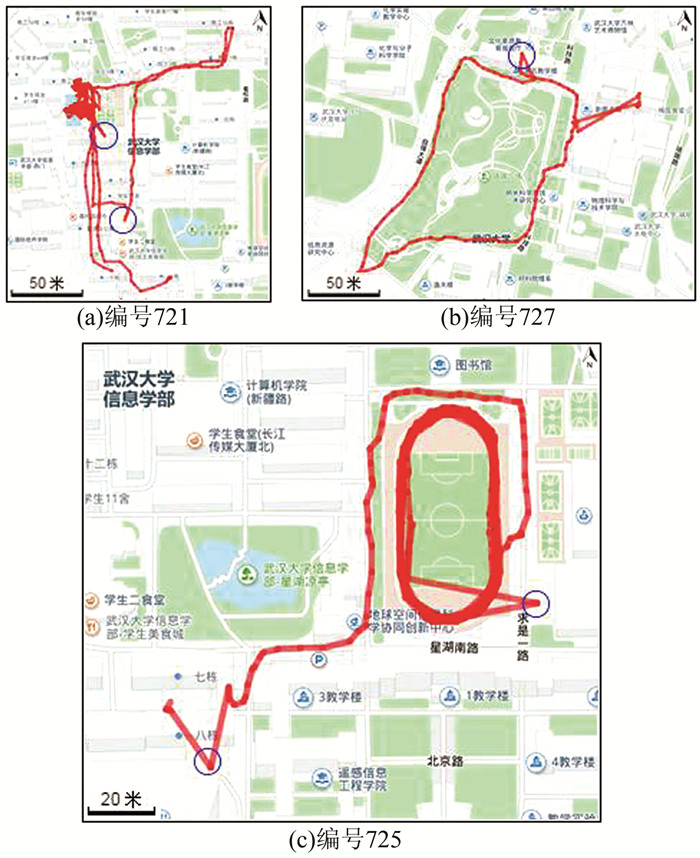 |
| 图 4 部分轨迹图 Figure 4 Trajectory Samples |
以725号轨迹为例进行处理。
3.1.1 轨迹分段计算每个轨迹点的转角,然后根据设定的阈值 (θ=π/3) 将轨迹中的转角点标记出来,进行抽稀处理后将轨迹分成了8段。将每一段自两端拐点向前后各扩展3个轨迹点作为一个处理单元,每个单元长度为25~60个轨迹点不等。
3.1.2 自相关分析对上一步得到的8个处理单元分别进行自相关分析,得到如图 5所示的8个自相关系数分布图。
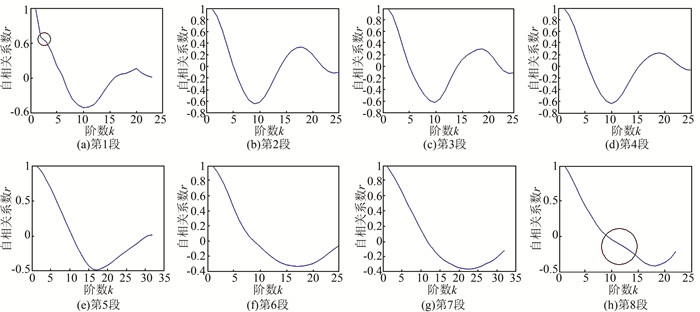 |
| 图 5 分段后自相关系数图 Figure 5 Autocorrelation Plots of Segmented Trajectories |
图 5中,横坐标表示自相关系数的阶数k,纵坐标表示自相关系数r。随着k增大,如果r迅速衰减,则说明序列稳定。
从图 5中明显可以看出,第2~7段满足随着k增大,r迅速平滑衰减并趋向稳定的特征,而第1段和第8段出现了衰减缓慢的地方 (图 5(a)和5(h)中圆圈处),说明这两段自相关序列不稳定,存在漂移点。随即对每一个自相关序列执行ADF检测,根据返回的结果也可以得出第1段和第8段为不稳定序列,存在漂移。因此,对分段后得到的轨迹处理单元进行ADF检测可以准确地检测漂移的存在。
采用文献[8]中的方法,即不对725号轨迹进行分段就计算整条轨迹的自相关系数,得到经度-时间序列的自相关系数分布图如图 6所示。
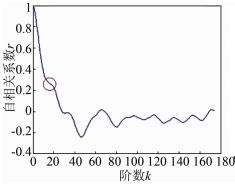 |
| 图 6 整条轨迹自相关系数图 Figure 6 Autocorrelation Plot of a Complete Trajectory |
从图 6可以看出,r在k=20附近衰减缓慢,说明该序列不稳定,该轨迹存在漂移。然而,对此轨迹进行ADF检测的结果表明此序列稳定,不存在漂移点,这与事实明显不符。说明文献[3]中这种对整条轨迹进行ADF检测的方法,处理结果是不精确的。
经分析,产生这种情况的原因在于自相关系数反映一个序列里所有数据的相关性,当样本数量较大时,其中一两个样本出现噪声对整体影响不大,并且用户不同运动方式形成的轨迹段间也有着差别,文献[3]中用来测试的数据采样间隔统一,数据来源的行进速度也基本一致,但平时采集到的数据应该是各种运动方式并存,这些不同运动方式之间的差别也会减小漂移对整体相关性的影响。
3.1.3 漂移点的判断和处理对存在漂移的第1和第8段的轨迹点速度序列进行统计分析,找到速度大小偏离均值一定阈值 (如3) 的点,第1段中为4、5号点,第8段中为172号点,见图 7中的方框部分。
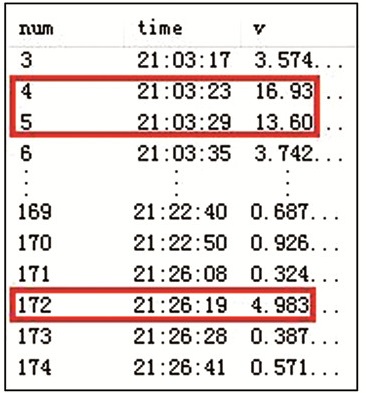 |
| 图 7 异常轨迹点速度图 Figure 7 Velocity Plot of Abnormal Trajectory Points |
根据速度公式进行分析,由于每一点的速度是以该点与前一点的距离除以两点的时间得到的,因此若出现连续两点速度异常 (如第1段中4、5号点),可判断4号点有漂移;而对第172号点,可以看到其前一点171号点的时间与170号点的时间相差4 min,而序列采样间隔约为5 s,可以判断这之间出现了接收机未收到信号的情况。因此可以得出172号点的速度异常应为171号点的漂移产生。
3.1.4 样本插值处理对存在漂移的4号、171号点进行样条插值处理,这里选取漂移点的前3个点作为参考点,时间值为插值条件,将修改后的结果替代原漂移点的经纬度得到新的轨迹。处理结果如图 8所示。
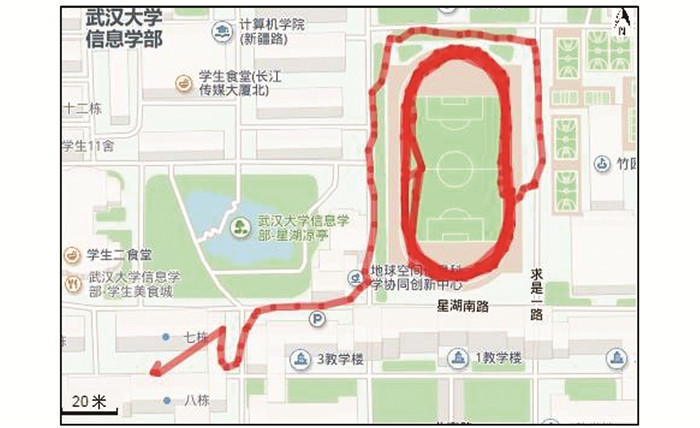 |
| 图 8 处理结果 Figure 8 Processed Trajectory |
3.2 结果与分析
将处理后得到的轨迹图与原图 (见图 4(c)) 进行对比,从图 8中可以看到,原轨迹中两个比较明显的漂移点都被算法找出,并进行了恰当的修正。
由于目前没有一个较好的漂移处理结果定量判断标准,为了进一步验证算法的准确性,从数据中随机抽取了130条轨迹,经过目视判断发现其中有40条轨迹存在明显的漂移,漂移点95个。本文的算法共检测出其中的87个,检测率91.5%,同时也存在少量未被目视判断为漂移点的正常轨迹点被检测出来,但发现经过插值处理后的结果影响较小。因此,可以证明本文提出的算法能够较好地发现轨迹中的漂移点,并得到比较合理的处理结果。
4 结束语本文在对GPS信号特点以及实际接收情况进行分析后,改进了基于时间序列的GPS轨迹漂移处理方法,提高了数据的准确度,消除或减少采集到的GPS轨迹中存在的漂移情况对其他分析结果的影响,以保证分析结果的准确性。在实际应用中可以用在相关GIS或者GPS软件产品中,以提高相关软件的实用性,同时减少开发成本。
本算法通过轨迹分段来减小不同运动方式和不同区域的轨迹段之间的影响,然后运用已经比较成熟的对时间序列自相关系数分析的理论方法对轨迹段进行分析,能迅速判断漂移的存在,并提高了判断的准确性。在自相关系数分析后得到的整体情况的基础上对轨迹点的速度属性逐一判别,即能找到具体的漂移点,并利用样条插值的方法进行处理。本文不仅在复杂度和计算量上做了优化,也解决了不同轨迹段对自相关系数存在干扰、漂移点较难发现的问题。
不足之处是以上的处理只是对接收到的GPS信号进行处理,不能从源头上消除漂移。同时本文的数据来源有限,没有进行较完善的分析评价。但随着相关算法和理论的不断完善以及硬件水平的提高,处理算法也会日益完善。
| [1] | 金国雄. 卫星定位的应用与数据处理[M]. 上海: 同济大学出版社, 2003. |
| [2] | 戴吾蛟, 丁晓利, 朱建军. 基于载噪比及参数先验信息的抗差模型[J]. 武汉大学学报·信息科学版, 2008, 33(8): 834–837. |
| [3] | 黄劲松, 刘峻宁, 刘成宝, 等. GPS信号载噪比研究[J]. 武汉大学学报·信息科学版, 2007, 32(5): 427–430. |
| [4] | 王泽民, 孟泱, 伍岳, 等. GPS、Galileo及其组合系统导航定位的DOP值分析[J]. 武汉大学学报·信息科学版, 2006, 31(1): 9–11. |
| [5] | Wolf J, Hallmark S, Oliveira M, et al. Accuracy Issues with Route Choice Data Collection by Using Global Positioning System[J]. Transportation Research Record: Journal of the Transportation Research Board, 1999, 1660(1): 66–74. |
| [6] | Schuessler N, Axhausen K W. Processing Raw Data from Global Positioning Systems Without Additional Information[J]. Transportation Research Record: Journal of the Transportation Research Board, 2009, 2105(1): 28–36. |
| [7] | 夏敬潮, 叶世榕, 刘炎炎, 等. WiFi辅助下附有高程信息的GPS定位[J]. 武汉大学学报·信息科学版, 2014, 39(1): 52–55. |
| [8] | 黄冠利, 王辉, 徐华平. 基于时间序列解决GPS信号定位漂移的研究[J]. 计算机工程与应用, 2008, (31): 94–97. |
| [9] | Percival D B, Walden A T. Wavelet Methods for Time Series Analysis[M]. Cambridge: Cambridge University Press, 2006. |
| [10] | Enders W. Applied Econometric Time Series[M]. NY: John Wiley & Sons, 2008. |
| [11] |
Cryer J D, Chanks.时间序列分析及应用:R语言[M].潘红宇.北京:机械工业出版社, 2011 |
| [12] | Dickey D A, Fuller W A. Likelihood Ratio Statistics for Autoregressive Time Series with a Unit Root[J]. Econometrica, 1981, 49(4): 1057–1072. DOI: 10.2307/1912517 |
| [13] | 李征航, 龚晓颖. 全球定位系统的新进展 (讲座四)--信号内部时延及其对钟差的影响[J]. 测绘地理信息, 2012, 37(4): 51–54. |
| [14] | Chang C, Zhou B. Multi-granularity Visualization of Trajectory Clusters Using Sub-trajectory Clustering[C]. IEEE International Conference on Data Mining Workshops, Miami, Florida, USA, 2009 |
 2017, Vol. 42
2017, Vol. 42


