| Lagrange修正的动态GM(1, 1)模型在基坑变形预测中的应用 | [PDF全文] |
2. 湘潭大学土木工程与力学学院,湖南 湘潭,411105;
3. 湖南天宇工程检测中心试验室,湖南 娄底,417000
2. College of Civil Engineering and Mechanics, Xiangtan University, Xiangtan 411105, China;
3. Hunan Tianyu Engineering Test Center Laboratory, Loudi 417000, China
基坑工程变形监测是为了及时了解在基坑施工过程中支护结构和邻近建(构)筑物、地下管线的变形规律及动态发展趋势,通过对基坑本身内部有关结构的位移及基坑外的环境保护对象的变形参数监测,验证基坑支护结构设计和基坑开挖施工组织设计的正确性; 并对基坑支护体系的稳定性、可靠性和安全性进行预测预报[1]。
常用的基坑变形预测模型有:时间序列模型、回归分析模型、BP神经网络模型、小波分析模型、灰色理论模型等。其中灰色GM(1, 1)(gray model)模型以其“小样本、贫信息”[2]的预测优势被广泛用于变形预测中。文献[3]指出灰色GM(1,1)通过对原始数据进行累加,使数据序列呈现出一定的规律性,但对于指数规律不明显的时间序列,预测效果不佳。文献[4]采用小波变换对监测数据进行消噪处理,取得了较好的效果,但对阈值函数的选取,并不能完全保留有用信号的小波系数。文献[5]采用单位时段差系数修正法对原始数据进行处理,通过实例验证了方法的可行性,但在外界因素影响较大的情况下,预测精度并不高。文献[6]指出采用指数函数对原始数据序列进行修正,取得了较好的效果,但是计算过程复杂,不易工程实现。文献[7]指出通过对初始值和背景值的优化,提高了传统模型的预测精度,但基坑沉降是一个动态过程,当原始监测数据出现扰动或遗漏时,缺乏对数据序列的修正分析。本文基于文献[8-10]的设计思路,提出一种基于Lagrange修正的动态GM(1, 1)模型,通过工程实践表明:Lagrange插值修正的动态GM(1,1)模型精度优于传统模型,基坑监测点的拟合预测值与实测值变形趋势一致。
1 Lagrange修正的动态GM(1, 1)模型建立Lagrange修正的动态GM(1, 1)模型基本思想是对原始数据采用Lagrange插值进行修正,消除原始序列中观测值误差或观测数据遗漏引起的扰动误差; 然后,将修正后的原始序列作为原始数据建立Lagrange插值修正的GM(1,1)模型; 最后,对修正后的模型实时引入最新的监测数据,剔除最旧的监测数据,建立Lagrange插值修正的动态GM(1,1)模型。
1.1 序列Lagrange插值修正设y=f(x)为基坑监测数据和其所对应时间节点的函数,通过对区间[a, b]上一系列节点
| $ l_{i}(x)=\frac{\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{i-1}\right)\left(x-x_{i+1}\right) \cdots\left(x-x_{n}\right)}{\left(x_{i}-x_{0}\right)\left(x_{i}-x_{1}\right) \cdots\left(x_{i}-x_{i-1}\right)\left(x_{i}-x_{i+1}\right) \cdots\left(x_{i}-x_{n}\right)}=\prod\limits_{j=0 \atop i \neq j}^{n} \frac{\left(x-x_{j}\right)}{\left(x_{i}-x_{j}\right)}, i=0, 1, 2, \cdots, n $ | (1) |
由上式可以看出, li(x)与节点有关,与f无关。
若
| $ L_{n}(x)=\sum\limits_{j=0 \atop i \neq j}^{n} \prod\limits_{j=0 \atop i \neq j}^{n} \frac{\left(x-x_{j}\right)}{\left(x_{i}-x_{j}\right)} y_{i}=\sum\limits_{i=0}^{n} \frac{\omega_{n}(x)}{\left(x-x_{i}\right) \omega_{n}^{\prime}\left(x_{i}\right)} y_{i} $ | (2) |
Lagrange插值实现步骤如下:
1) 输入
2) 计算插值L(u),输入插值点u,v=0,对j=0, 1, …, n做
利用Matlab编程[11]并执行Lagrange算法,操作流程如图 1所示。
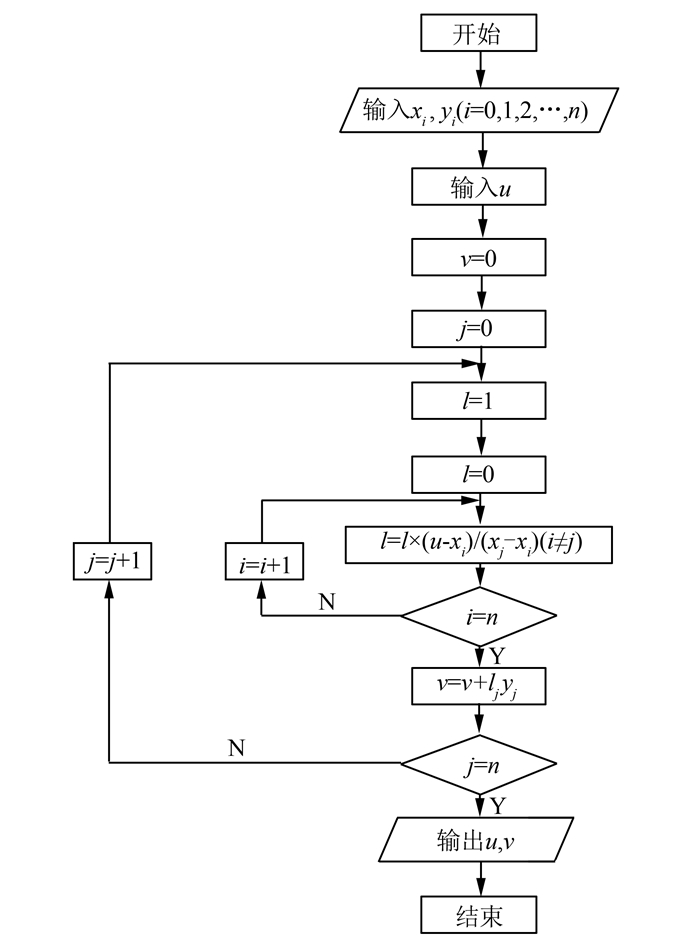 |
| 图 1 Lagrange算法流程图 Fig.1 Flow Chart of Lagrange Algorithm |
1.2 传统GM(1, 1)模型
传统GM(1, 1)模型步骤如下:
1) 原始序列生成。
利用s(0)来表示基坑变形的实际监测数据,s(0)={s(0)(1),s(0)(2),s(0)(3),…,s(0)(n)}
2) 1-AGO序列生成。
s(1)={s(1)(1),s(1)(2),s(1)(3),…,s(1)(n)}。其中,
3) 背景值生成。
设
4) 建立白话方程。
5) 求解参数:根据最小二乘法原理,令
其中,
6) 白话方程响应式为:
| $ \begin{aligned} \hat{s}^{(1)}(k+1) &=\left[s^{(0)}(1)-\frac{b}{a}\right] \mathrm{e}^{-a k}+\frac{b}{a} \\ k &=1, 2, 3, \cdots, n \end{aligned} $ | (3) |
7) 建立预测方程:对上式进行累减得,
| $ \begin{aligned} \hat{s}^{(0)}(k+1)=&\left(1-\mathrm{e}^{a}\right)\left[\hat{s}^{(0)}(1)-\frac{b}{a}\right] \mathrm{e}^{-a k} \\ k &=1, 2, 3, \cdots, n \end{aligned} $ | (4) |
传统GM(1, 1)模型采用的是t=n时的数据进行建模,基坑沉降是一个动态过程,旧信息对预测的贡献较弱,新信息更能代表基坑的变形趋势。其建模原理为将传统GM(1, 1)模型中的原始序列s(0)={ s(0)(1),s(0)(2),s(0)(3),…,s(0)(n) }的最旧信息s(0)(1)去掉,同时加入最新信息s(0)(n+1),利用新的监测序列s(0)={s(0)(2),s(0)(3),s(0)(4),…,s(0)(n+1)}重新建模,随着时间序列的发展,反复依次递补,这种模型即为动态GM(1, 1)模型。与传统模型相比,动态GM(1, 1)以
| $ s^{(1)}(k+1)=\left[s^{(1)}(m)-\frac{b}{a}\right] \mathrm{e}^{-a(k-n+1)}+\frac{b}{a} $ | (5) |
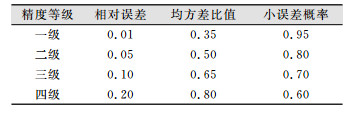
为了判断Lagrange修正的动态GM(1, 1)模型的可靠性,需对其质量进行评价,常用的精度检验方法有残差检验、后验差检验。设原始序列s(0)(k)和残差序列ε(0)(k)的方差分别为S12、S22,则有:
| $ \begin{array}{l} S_{1}^{2}=\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(s^{(0)}\left(k_{i}\right)-\bar{x}\right)^{2} \\ S_{2}^{2}=\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(\varepsilon^{(0)}\left(k_{i}\right)-\bar{\varepsilon}\right)^{2} \end{array} $ | (6) |
式中,
| 表 1 灰色模型精度检验参照表 Tab.1 Gray Model Accuracy Test Reference Table |
 |
2 工程实例
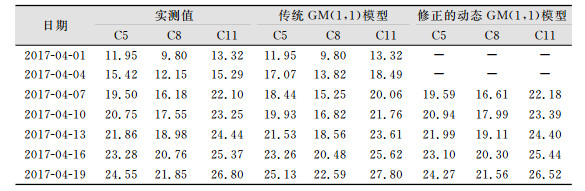
湖南省某中心医院地下室基坑项目,位于新星南路与湘阳街交接处。该基坑项目东面和南面各有一栋建筑紧挨建筑,东面建筑物5F为医院办公楼,南面建筑物为高层,基坑等级为一级,场地复杂。分别选取基坑开挖过程中具有代表性沉降监测点C5、C8、C11的10期监测数据进行分析,用前7期数据进行建模,对后3期数据进行预测。具体步骤为:①采用Lagrange插值法对原始序列进行修正; ②使用监测点的1~7期修正数据作为原始序列进行一次累加建立模型,③去掉第1期数据,使用2~8期修正的监测数据进行建模。同理,使用3~9期修正的数据进行建模。采用未经过Lagrange插值修正的传统GM(1, 1)模型和Lagrange插值修正的动态GM(1,1)模型分别对实例数据进行拟合预测,结果见表 2、表 3。其中实际观测数据为累计沉降值。
| 表 2 两种模型拟合结果检验表/mm Tab.2 Test Results for Fitting Two Models/mm |
 |
| 表 3 两种模型预测结果检验表/mm Tab.3 Test Results of Two Model Predictions/mm |
 |
由表 2、表 3可知,利用残差合格模型对两种模型的拟合效果进行精度评定,分析可得,基坑监测点C5、C8和C11传统GM(1,1)模型的平均相对中误差为4.01%、5.11%和7.48%,即监测点C5、C8和C11的精度分别为二级、三级和三级。采用Lagrange修正的动态GM(1,1)模型模型对基坑监测点进行预测,监测点C5、C8和C11预测精度等级分别为一级、二级和二级。评定结果见表 4。
| 表 4 监测点拟合预测精度评定表 Tab.4 Monitoring Point Fitting Prediction Accuracy Assessment Form |
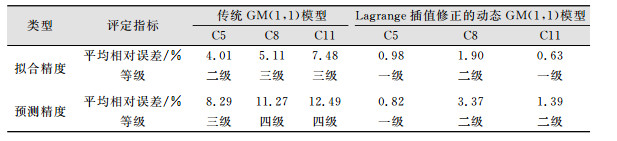 |
由表 4可得, Lagrange修正的动态GM(1,1)模型预测精度高于传统模型,随着数据序列的不断修正与递补,监测点的预测变形趋势与实际变形趋势基本一致。
3 结束语本文通过采用Lagrange插值法对原始序列进行修正,消除原始序列中观测误差或数据遗漏对模型预测的影响,利用修正过的数据作为原始数据进行建模,并实时引入新信息代替旧信息,建立Lagrange插值法修正的动态GM(1, 1)模型。通过对某基坑进行实证分析,Lagrange插值法修正的动态GM(1, 1)模型精度优于传统模型,更能反映出基坑的变形状态和趋势。
| [1] |
王景环, 豆红磊, 刘龙飞, 等. 基于优化GM(1, 1)在基坑变形预测中的应用研究[J]. 矿山测量, 2018, 46(1): 18-21. DOI:10.3969/j.issn.1001-358X.2018.01.005 |
| [2] |
张拯, 张献州, 罗保林, 等. 基于灰主成分分析法的变形信息提取研究[J]. 铁道科学与工程学报, 2017, 14(7): 1 369-1 375. |
| [3] |
邓聚龙. 灰色系统理论教程[M]. 武汉: 华中理工大学出版社, 1990.
|
| [4] |
容静, 文鸿雁, 周吕. 一种改进灰色预测模型在变形预测中的应用[J]. 测绘科学, 2017, 42(3): 35-38. |
| [5] |
孙泽信, 庞逸群, 黄腾. 改进的灰色模型在建筑物沉降预测中的应用[J]. 测绘工程, 2010, 19(3): 59-62. DOI:10.3969/j.issn.1006-7949.2010.03.017 |
| [6] |
孙永荣, 胡应东, 陈武, 等. 基于GM(1, 1)改进模型的建筑物沉降预测[J]. 南京航空航天大学学报, 2009, 41(1): 107-110. DOI:10.3969/j.issn.1005-2615.2009.01.021 |
| [7] |
邹进贵, 聂海滨, 邱国庆. 一种同时优化背景值和初始条件的GM(1, 1)建模方法[J]. 测绘地理信息, 2018, 43(2): 79-82. |
| [8] |
黎洋, 花向红, 姚周祥, 等. 傅里叶级数修正的动态GM(1, 1)模型在沉降预测中的应用[J]. 测绘地理信息, 2017, 42(1): 30-33. |
| [9] |
成枢, 冯子帆, 郭祥琳, 等. 不同灰色GM(1, 1)模型在地铁沉降预测中的效果分析[J]. 测绘地理信息, 2019, 44(1): 14-17. |
| [10] |
赵磊磊, 花向红, 邵梽, 等. 改进的新陈代谢GM(1, 1)模型在建筑物沉降预测中的应用[J]. 测绘地理信息, 2019, 44(6): 120-122. |
| [11] |
魏鑫. MATLAB R2014a从入门到精通[M]. 北京: 电子工业出版社, 2015.
|
 2020, Vol. 45
2020, Vol. 45

