| 一种无偏估计的离差加权建筑物沉降监测资料插补方法 |
2. 武汉大学灾害监测和防治研究中心, 湖北 武汉, 430079
2. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China
在建筑物的建设过程中, 变形监测对工程的施工与运营管理有着重要的意义[1, 2]。变形监测工作要求能精确、安全、长期地采集数据[3],但在建筑物的建设期内,时常会出现个别建筑物监测点损毁、漏测的情况[4]。为了保持监测资料的完整性及变形分析的需求,需要对缺漏的数据资料进行插补。目前常用的方法,一类是依据时间序列,主要有均值填补法[5]、热平台填补法[6]、最邻近填补法和回归填补法[7]等;另一类是根据其物理特性和时空相关性按照距离加权运算,其中主要的插值方法有反距离加权法,这类方法往往直接通过周围观测点的值内插,或者通过特定的数学公式内插,较少考虑观测点的空间分布情况[8]。基于此,本文提出依据空间变异规律建立对观测点的空间相关分析,利用空间内相关测点进行插值,从而得到待估点位的无偏估计量。工程实例说明,本文方法可以有效地运用于建筑物变形监测资料的插补应用。
1 沉降监测资料插补方法建筑物变形监测中的形变量具有空间分布特征,既有随机性又有结构性,样本间具有空间相关性,所以随空间位置x变化而变化的形变量z(x)解释为随机变量z(x)的一次具体实现。现设位于x0处的形变估计值为z*0,是周围若干实测点形变量z(xi)(i=1, 2, …, n)的线性组合,即
| $ z_0^ * = \sum\limits_{i = 1}^n {{\lambda _i}} z({x_i}) $ | (1) |
式中,λi为权重;z(xi)为周围测点形变量;z*0为x0处的形变估计值。
实际建筑物变形监测中的形变量往往呈现空间上的相关性,依据建筑物基础形变特性,可以认为在一定空间尺度内,区域化的形变量满足二阶平稳假设:
| $ E(z_0^ * ) = E(\sum\limits_{i = 1}^n {{\lambda _i}} z({x_i})) = \sum\limits_{i = 1}^n {{\lambda _i}} E(z({x_i})) = \sum\limits_{i = 1}^n {{\lambda _i}} m $ | (2) |
其数学期望E(z(xi))=m为常数,方差存在且平稳。只需
在形变估计值z*0的周围有n个实测点形变量z(xi)(i=1, 2, …, n),对其进行统计,其平均值z(x)为:
| $ \overline {z(x)} = \frac{1}{n}\sum\limits_{i = 1}^n {z({x_i})} $ | (3) |
这n个形变量中,假定在一定抽样尺度内,沉降形变量基本一致,采用离差di=z(xi)-z(x)的平方作为赋权的依据,各离差值的大小直接反映了该实测点与待测点的变形一致程度。权重λi的计算公式如下:
| $ {\lambda _i} = \frac{{\frac{{\sum {{d^2}} }}{{d_i^2}}}}{{\sum {\left( {\frac{{\sum {{d^2}} }}{{d_i^2}}} \right)} }} $ | (4) |
| $ \frac{{{\lambda _i}}}{{{\lambda _j}}} = \frac{{\frac{{\sum {{d^2}} }}{{d_i^2}}}}{{\frac{{\sum {{d^2}} }}{{d_j^2}}}} = \frac{{d_j^2}}{{d_i^2}} $ | (5) |
| $ \sum\limits_{i = 1}^n {{\lambda _i}} = 1 $ | (6) |
式中,λi、λj为权重;di、dj为高差。
满足式(5),说明各测点的权重与该点离差的平方成反比;满足式(6),则说明待插点即为各实测值的无偏估计。
1.2 异常值检测在对建筑物进行变形分析时,常常遇到某些监测点数据异常,其中包括某些点位沉降规律与周围点位不一致的情况。此时,利用上述方法分别对变形监测中各测点逐一进行插值计算,得到该点位的插值z*i(i=1, 2, 3, …, n)、各点位实际测量值zi与插值z*i之差为Δi,即Δi=zi-z*i。利用中误差知识,由有限个观测值的真误差求得中误差的估值[9],得到:
| $ \sigma = \sqrt {\frac{{\sum\limits_{i = 1}^n {{\Delta _i}^2} }}{n}} $ | (7) |
依据极限误差的概念,由于P(-3σ < Δ < 3σ)=99.7%,故以Δlim=3σ作为偶然误差的极限值,Δlim称极限误差,逐一比较各个Δi与Δlim的大小,若Δi < Δlim,则表示该点位合格;否则,说明该点位存在异常。
1.3 插值区域选取利用同区域内形变规律基本一致这一假定进行插值,其问题的关键在于插值区域的确定,即变程a(影响半径)的确定。若变程a选取偏大,则会导致参与插值计算的点位过多,数据过度平滑,降低区域内的空间相关性;若变程a选取偏小,抽样尺度过小,即会增加区域化变量z(xi)内部的随机性,无法反应真实的变化规律。本文依据采样点的距离,提出两种参考指标确定插值区域。第一种以各测点间的平均距离Lmean为依据,分别以Lmean、
为了验证本文方法的可行性,现利用位于武汉市某小区建筑物沉降变形监测成果,选取部分较有代表性的监测资料进行实例验证分析。该住宅小区某高层建筑物总共布设了18个测点,选取某一期沉降观测采集的17个观测值(4号点损毁,无法测量),布设测点点位图如图 1所示。根据各个监测点的坐标值计算出各点间的距离,该栋建筑物沉降观测点间的最小间距出现在1与2号测点之间,为3.80 m;最大间距出现在7与14号测点之间,为34.85 m,各测点间平均距离(Lmean)为15.28 m,取变程a=
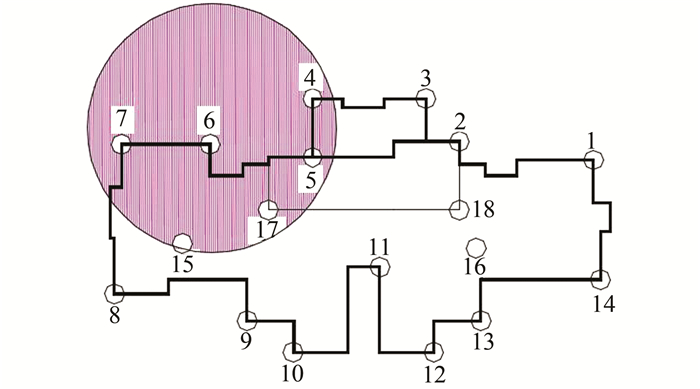 |
| 图 1 建筑物沉降变形监测点布设图 Figure 1 Layout of Monitoring Points for Settlement Deformation of the Building |
2.1 异常值检验及插值精度比较
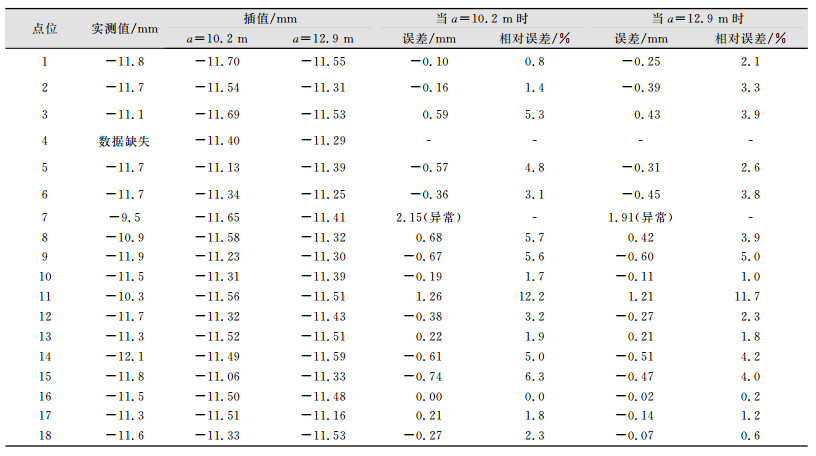
应用本文所述插值方法,分别使用变程a=10.2 m和a=12.9 m进行点位搜索,遍历各个点位逐一进行插值计算,并将插值结果与实测值进行比较,统计结果如表 1所示。同时计算两种插值结果与测量值之差的中误差,结果如表 2所示。
| 表 1 插值结果统计表 Table 1 Interpolation Result |
 |
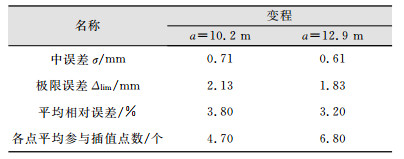
| 表 2 实测值与插值之差统计表 Table 2 Difference Between Measured Value and Interpolation |
 |
由表 1可以看出,以变程a=10.2 m为影响半径进行插值计算,极限误差Δlim=2.13 mm,查找表 1中发现7号点的差值2.15 mm > Δlim,而其余各差值则明显小于极限误差Δlim,所以认为7号点为异常点位。同样,以变程a=12.9 m计算也得到7号点为异常点位。经事后验证,7号点位由于施工破坏,测量数据发生错误,以上两种检测方法均可以找出异常点位7。
参考表 2中平均插值点个数,以变程a=10.2 m为半径内平均有4~5个点参与插值,而以变程a=12.9 m为半径则有约7个点参与插值。表 1中以变程a=12.9 m计算得到的各点插值结果,最大值为14号点位的-11.59 mm,最小值为17号点位的-11.16 mm,各点插值结果差异较小,这是由于增大了变程a,导致过度平滑数据而造成。虽然以变程a=12.9 m插值中误差σ和平均相对误差都比a=10.2 m的插值结果略小,但过度的数据平滑不但会掩盖抽样点的差异,而且计算量也明显增大,同时以平均距离Lmean作为变程的参考依据则更全面地反映了点位之间的距离不会因为监测布设的不同而造成数据过分缺失和冗余,在满足异常值检测的前提条件下,本文认为以平均距离Lmean作为变程的参考更符合插值要求。
2.2 异常值附近插值结果比较为比较局部点位异常值对插值精度的影响,选取紧邻异常点位7附近的6号点进行插值验证,分别以异常点位7参与插值与剔除异常点位7后的插值结果精度进行比较。经计算,在异常值参与插值的情况下,插值误差为-0.36 mm,相对误差为3.1%;剔除异常值的情况下,误差达到了-0.02 mm,相对误差更是达到了0.2%,插值精度高。
经过多期数据检核验算后证明,采用先检测异常情况的方法,如果待插值点位在局部异常值影响范围以内,则采用剔除异常值后再进行插值的方式精度更高。
2.3 远离异常值区域插值结果比较为了比较在远离异常影响的区域插值结果的精度,现以点1为例进行插值。经计算,当变程a=10.2 m时,即在10.2 m的影响半径内有4个点参与插值,其中不包含异常点位7,最后计算得到的沉降值为-11.70 mm,与实际形变值之差为0.10 mm,相对误差达到0.84%;经过点位精度比较,由于异常值不参与插值,所以点位的精度较高,完全达到了工程要求。
综合以上数据,笔者认为,在进行变形监测数据处理时,可以先依据本文方法进行异常数据的检测,若存在异常点位,则应查找数据异常的原因。需要进行数据插补时,则先进行异常值检测,若在异常值附近插补数据,则需剔除异常值,插值精度较高。
3 结束语本文针对建筑物形变监测数据插补,提出了基于离差的定权方法,同时阐述了异常值的检验原理。实验结果表明,该方法可以有效地检测出点位形变的异常情况,减少数据异常干扰。综上所述,本文提出的基于离差定权的建筑物沉降监测资料插补方法是可行的,对于变形监测资料的检核和数据插补都有一定的实用价值。
| [1] |
黄声享, 尹晖, 蒋征.
变形监测数据处理[M]. 2版. 武汉: 武汉大学出版社, 2010 .
Huang Shengxiang, Yin Hui, Jiang Zheng. Deformation Monitoring Data Processing[M]. 2nd ed. Wuhan: Wuhan University Press, 2010 . |
| [2] |
林勋.时间序列分析在建筑物变形监测中的应用[D].吉林:吉林大学, 2005 Lin Xun. Application of Time Series Analysis in Deformation Monitoring of Buildings[D]. Jilin:Jilin University, 2005 http://cdmd.cnki.com.cn/Article/CDMD-10183-2006014378.htm |
| [3] |
吴江淮.建筑物静态变形监测数据分析与处理[D].上海:同济大学, 2007 Wu Jianghuai. Analysis and Treatment of Building Static Deformation Monitoring Data[D].Shanghai:Tongji University, 2007 http://cdmd.cnki.com.cn/Article/CDMD-10247-2007050106.htm |
| [4] |
柯善亮, 邱卫宁, 花向红. 基于监测点相似性的变形监测预测模型与数据修复[J].
勘察科学技术,2012,(5) : 9–11.
Ke Shanliang, Qiu Weining, Hua Xianghong. Prediction Model and Data Restoration of Deformation Monitoring Based on Similarity of Monitoring Points[J]. Survey Science and Technology,2012,(5) : 9–11. |
| [5] |
杜琨.变形监测数据处理的方法研究[D].长沙:中南大学, 2013 Du Kun. Research on the Method of Data Processing for Deformation Monitoring[D].Changsha:Central South University, 2013 |
| [6] | Rao J N K, Shao J. Jackknife Variance Estimation with Survey Data under Hot Deck Imputation[J]. Biometrika,1992,79 : 811–822. DOI:10.1093/biomet/79.4.811 |
| [7] | Bello A L. Imputation Techniques in Regression Analysis: Looking Closely at Their Implementation[J]. Computational Statistics and Data Analysis,1995,20 : 45–57. DOI:10.1016/0167-9473(94)00024-D |
| [8] |
孙然好, 刘清丽, 陈利顶. 基于地统计学方法的降水空间插值研究[J].
水文,2010,30(1) : 14–18.
Sun Ranhao, Liu Qingli, Chen Liding. Research on Spatial Interpolation of Precipitation Based on the Geo-statistics Method[J]. Hydrology,2010,30(1) : 14–18. |
| [9] |
武汉大学测绘学院测量平差学科组.
误差理论与测量平差基础[M]. 2版. 武汉: 武汉大学出版社, 2009 .
Adjustment Subject Group of School of Geodesy and Geomatics, Wuhan University. Error Theory and Measurement Adjustment[M]. 2nd ed. Wuhan: Wuhan University Press, 2009 . |
 2016, Vol. 41
2016, Vol. 41

