| 全球单层电离层球谐函数模型计算及精度评估 |
2. 中国矿业大学(北京)地球科学与测绘工程学院,北京,100083;
3. 61243部队,新疆 乌鲁木齐,830006
2. School of Geosciences and Surveying and Mapping Engineering, China University of Mining and Technology (Beijing), Beijing 100083, China;
3. Troops 61243, Urumqi 830006, China
地表以上50 km至磁顶层这段空间称为电离层[1]。为简化电离层研究,人们通常采用电离层薄层模型,即认为天顶方向总电子含量(vertical total electron content,VTEC)都集中分布在一个无限薄层的球面上[2],假想薄层高度在350~450 km,电离层电子密度极值在这个高度范围内。对于同一组观测资料,选择不同电离层参考坐标系会出现不同规律分布[3],考虑到薄层模型在时空上的四维变化的特性,将日固、地固与地理、地磁两两组合可得到常用的4种全球卫星导航系统(global navigation satellite system,GNSS)电离层研究坐标系[4]。
GNSS系统以高轨道、全天候及完善的星座空间分布等特点对电离层活动进行长时间、全方位的观测,国际GNSS服务组织(International Global Navigation Satellite System Service,IGS)也提供了丰富的电离层研究资源,使GNSS成为电离层研究的重要工具[5]。通过测定电磁波在电离层中信号延迟来确定电子密度,建立全球电离层数值模型[6]。电离层研究模型既包括利用丰富的观测数据借助公式拟合的经验模型(如多项式模型),又包括虽精度较低但定性描述电离层特征的理论模型[7]。此外,电离层层析等建模技术也有较大进展[8-10]。本文利用球谐函数对电离层建模,并选取IGS在全球范围内布设的224个连续跟踪站观测文件作为数据来源,以反演电离层电子密度,将结果与IGS全球服务组织CODE(center orbit determination Europe)中心的数据比较,发现具有良好的精度。本文分时间段统计2016-01海洋测高卫星Jason-2观测数据与反演结果相对比例因子k,发现两种数据间具有良好的一致性,在此基础上统计了两种数据的差值,进一步验证了模型精度。
1 单层电离层球谐函数模型球谐函数有着优良的数学结构,电离层研究常采用此模型以描述全球VTEC时空分布及变化,其计算公式为:
| $ E\left( {\beta , s} \right) = \sum\limits_{n = 0}^{{n_{\max }}} {\sum\limits_{m = 0}^n {{{\tilde P}_{nm}}} } \left( {\sin \beta } \right)\left( {{a_{nm}}\cos ms + {b_{nm}}\sin ms} \right) $ | (1) |
式中,E(β,s)代表VTEC;β为穿刺点的地理纬度或者地磁纬度;s = λ-λ0为日固系中穿刺点的经度,其大小与地方时有关,λ为穿刺点的地理经度,λ0为太阳的精度;nmax为二维泰勒级数展开纬度方向的最大阶数。
若仅考虑电磁波频率,衡量电离层中电磁波传播时间延迟ΔTion可表达为[11]:
| $ \Delta {T_{{\rm{ion}}}} = \frac{{40.28}}{{{f^2}}}{\rm{TEC}} $ | (2) |
式中,ΔTion为电磁波时间延迟,单位为s;TEC(total electron content)为总电子含量。
GNSS卫星包括测码伪距观测值P及载波相位观测值L,观测方程分别为:
| $ \left\{ \begin{array}{l} P = \rho + c\left( {{\rm{d}}{t_{接}} - {\rm{d}}{t_{卫}}} \right) + \Delta {T_{{\rm{ion}}}} + \Delta {T_{{\rm{tro}}}} + \Delta {D_{{\rm{rel}}}} + \\ \;\;\;\;\;\;c{B_r} + c{B_s} + M + \varepsilon \\ L = \rho + c\left( {{\rm{d}}{t_{接}} - {\rm{d}}{t_{卫}}} \right) + \Delta {T_{{\rm{ion}}}} + \Delta {T_{{\rm{tro}}}} + \Delta {D_{{\rm{rel}}}} + \\ \;\;\;\;\;\;c{b_r} + c{b_s} + M + \varepsilon + \lambda N \end{array} \right. $ | (3) |
式中,ρ为卫星到接收机几何距离;c为理论光速;dt接为接收机钟差;dt卫为卫星钟差;ΔTion为电离层延迟;ΔTtro为对流层延迟;ΔDrel为相对论效应;Br和Bs分别为码观测中接收机和卫星硬件延迟;br和bs分别为载波相位观测中接收机和卫星硬件延迟;M为多路径效应影响;ε为噪声扰动项;λ为电磁波波长;N为整周模糊度。观测方程中包括电离层延迟误差和对流层延迟误差等误差影响。
在两个频率间对测码和测相伪距求差,综合两类观测值的长处及球谐模型得到全球电离层建模的球谐函数为:
| $ \begin{array}{*{20}{c}} {\sum\limits_{n = 0}^{{n_{{\rm{max}}}}} {\sum\limits_{m = 0}^n {{{\tilde P}_{nm}}} } ({\rm{sin}}\beta )({a_{nm}}\cos ms + {b_{nm}}{\rm{sin}}ms) = }\\ {{\rm{cos}}({\rm{arcsin}}(\frac{R}{{R + H}}{\rm{sin}}(\alpha z))) \times }\\ {[ - \frac{{f_1^2f_2^2}}{{40.3(f_1^2 - f_2^2)}}({P_{4, sm}} - c{\rm{DC}}{{\rm{B}}_r} - c{\rm{DC}}{{\rm{B}}^s})]} \end{array} $ | (4) |
式中,P4,sm为平滑伪距[11];R为地球半径;H为电离层薄层高度;anm、bnm为球谐模型系数;DCBr为接收机硬件延迟单差,是待求未知数;DCBS为卫星硬件延迟单差。本文假定GNSS卫星与接收机硬件延迟较为稳定,一天解算一次;并假设同类卫星的硬件延迟之和为0以简化计算。一般情况下,球谐模型系数anm、bnm每2 h解算一次。
2 数据验证选取2016-02-05为研究对象,其年积日为36,积累周为1 882,收集精密星历SP3文件,RINEX观测文件(O文件),CODE电离层文件,2016-02平均DCB(different code Bias)文件以验证模型可行性及精度。本文采用电离层薄层模型,薄层高度为距地506.7 km,同时将电离层划分为经度分辨率为5°且纬度分辨率5°的格网。选取IGS在全球范围内布设的224个连续跟踪站作为观测文件数据来源,球谐函数采用15阶展开。数据要求为研究日期在内前后连续3 d的精密星历文件SP3和RINEX观测文件(O文件),研究日期当天及前一日电离层文件,当月平均DCB文件。
本文模型每隔两小时解算一次电离层VTEC,其时间节点分别为UT 0:00、UT 2:00、UT 4:00、…、UT 22:00,总计12组VTEC格网数据。与CODE相比,各时段差值显示了模型具有一定精度,如图 1所示。
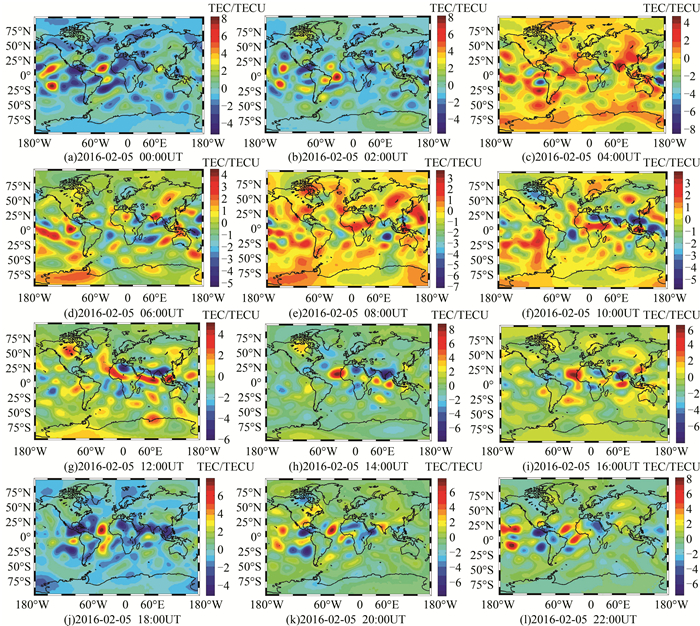 |
| 图 1 2016-02-05各时段VTEC差值分布图 Fig.1 VTEC Differential Distribution Chart at Time on February 5, 2016 |
3 与海洋测高卫星比较
海洋测高卫星为一种太阳同步卫星,测高原理为星载测高仪于卫星轨道面不断垂直于水面发射微波,记录接收回波信号时间,进而得到水面相对某一参考椭球面高度,在求得海平面大地高同时,亦可获得VTEC。海洋测高卫星轨道高度约为1 350 km,而GNSS卫星如GPS卫星其轨道高度为20 200 km。在距地高度1 350~20 200 km仍存在一定含量的VTEC,欲以测高数据为基准比较模型精度,引入相对比例因子k,将GNSS卫星轨道内推至测高卫星轨道高处。模型为格网数据,而海洋测高数据为与若干点状数据集合,采用双线性内插法由格网模型生成测高卫星对应地点模型VTEC来作比较分析。对海洋测高数据,本文采用30 s连续平滑预处理以剔除异常值,其中海洋测高卫星数据采用Jason-2卫星观测值。
因Jason-2卫星反演所得的VTEC与GNSS反演结果覆盖高度范围不同,Jason-2卫星反演VTEC仅为GNSS反演结果的一部分,为建立两者反演VTEC间的换算关系,在两者反演VTEC间建立线性回归方程,方程斜率k(即为相对比例因子k),而采用线性回归方程相关系数R2来衡量Jason-2数据与模型数据间的相关性。
由于Jason-2卫星只有一颗且为太阳同步卫星,其轨道倾角约为66°,重访周期为10 d。在一定周期内,特定UT时间段卫星会扫过特定区域。本文以UT时为基准,将UT 0~22 h等分为6段,统计2016-01数据,统计结果如表 1所示。数据间相关系数R2接近1,验证了模型精度。
| 表 1 分时间段统计k值 Tab.1 Time Period Statistics k |
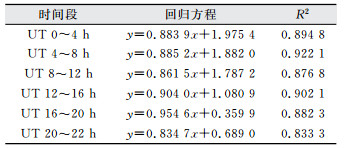 |
各纬度带k值取值即为表 1中回归方程中斜率,以Jason-2观测数据为基准,为进一步验证模型精度,选用2016-02-05~2016-02-12(剔除02-08磁暴数据)数据,采用k值将模型数据内缩至Jason-2轨道高度,内插并与海洋测高卫星数据作差,图 2为各时段残差统计图,每日内各时段残差分布趋于一致,且残差集中于1 TECU内显示了模型具有较高精度。
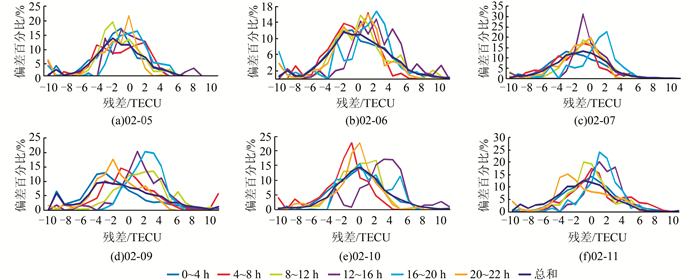 |
| 图 2 各日各时段残差对比 Fig.2 Difference in the Residual Difference of Each Day |
4 结束语
本文推导建立了基于球谐函数的电离层延迟模型,并利用基于球谐函数的电离层时间延迟模型计算了2016-02-05的全球电离层格网电子密度,给出了13个时段电离层全球电离层格网地图GIM(global ionospheric map),同时,以海洋测高数据(Jason-2观测数据)为基准,分时间段讨论了相对比例因子k的取值,以2016-01为研究对象进行了详细的探求,在求得相对比例因子k后,利用2016-02-7的数据将GNSS卫星轨道内缩至Jason-2轨道高度统计残差并进行了分析,进一步验证模型的可行性和精度。
| [1] |
韩玲.区域GPS电离层TEC监测、建模和应用[D].上海: 中国科学院上海天文台, 2006 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1616602
|
| [2] |
Mannucci A J, Wilson B D, Yuan D N, et al. A Global Mapping Technique for GPS Derived Ionospheric Total Electron Content Measurements[J]. Radio Science, 1998, 33(3): 265-582. |
| [3] |
徐文耀. 地磁与空间物理资料的组织和相关坐标系[J]. 地球物理学进展, 2006, 21(4): 1043-1060. DOI:10.3969/j.issn.1004-2903.2006.04.002 |
| [4] |
袁运斌.基于GPS的电离层监测及延迟改正理论与方法的研究[D].武汉: 中国科学院测量与地球物理研究所, 2002 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y568495
|
| [5] |
黄逸丹.区域电离层GPS监测及应用研究[D].上海: 中国科学院上海天文台, 2007 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1620854
|
| [6] |
Lanyi G E, Roth T. A Comparison of Mapped and Measured Total Ionospheric Electron Content Using Global Positioning System and Beacon Satellite Observations[J]. Radio Science, 2016, 23(4): 483-49. |
| [7] |
蔡昌盛, 高井祥. 利用GPS观测值反演电离层总电子含量的时空变化[J]. 辽宁工程技术大学学报(自然科学版), 2009, 28(5): 727-730. DOI:10.3969/j.issn.1008-0562.2009.05.011 |
| [8] |
闻德保.基于GPS的电离层层析算法及其应用研究[D].武汉: 中国科学院测量与地球物理研究所, 2007 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1623154
|
| [9] |
曹文涛, 郭际明, 谢翔, 等. 基于CORS的电离层延迟建模方法[J]. 测绘地理信息, 2013, 38(3): 12-16. |
| [10] |
韩吉德, 王祖顺, 王春青. 全球电离层时空变化特性分析[J]. 测绘地理信息, 2012, 37(6): 26-29. |
| [11] |
Hofmann-Wellenhof B, Lichtenegger H, Collins J. Global Positioning System Theory and Practice[M]. New York: Springer-Verlag, 2001.
|
 2018, Vol. 43
2018, Vol. 43

