| 基于球谐分析的EMM-740的计算及实现 |
2. 海军工程大学导航工程系,湖北 武汉, 430033;
3. 广州海洋地质调查局, 广东 广州, 510440
2. Department of Navigation, Naval University of Engineering, Wuhan 430033, China;
3. Guangzhou Marine Geological Survey, Guangzhou 510760, China
地磁场是矢量场,是重要的地球物理场之一,有复杂的空间结构和时间演化,是空间位置和时间的函数。地磁场的观测和研究结果直接或间接地服务于社会各个领域,如能源和矿产资源探查,飞机和船舶导航,无线电通讯,航天环境监测,自然灾害预测等[1-4]。
为了快速、准确地获得测点地磁场值,需要编写计算精度高、可计算的时间范围长、可移植和可靠性好的程序[5]。高德章[6]列出了国际地磁参考场(international geomagnetic reference field,IGRF)(1900~1995年)的球谐系数,并详细叙述了计算的步骤;肖胜红等[7]实现了IGRF模型(1900~2010年)全球任意位置的磁场值计算和等值线图绘制;冯春[8]计算了IGRF模型(1900~2010年)总场强F,并绘制了F的等值线;柴松均等[5]完成了任意位置的IGRF模型(2010~2015年)的磁场值计算;刘元元等[9]实现了基于球谐分析的720阶次的增强地磁场模型(enhanced magnetic model,EMM)(2010~2015年)的计算。综上所述,国内在模型实现方面取得了诸多有价值的成果,但目前地磁场模型的实现软件大多是基于IGRF模型,而EMM模型比IGRF模型精度更高,但EMM的实现软件研究较少,现有软件与美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration,NOAA)公布的模型的计算结果相比,精度不够高。此外,现有的EMM模型研究中,在使用NGDC-720模型时,NGDC的720阶次是基于椭球谐分析的,但椭球谐分析转为球谐分析时使用的却是740阶次,该认知的错误导致计算结果有偏差。鉴于此,本文结合前人的研究思路和成果,基于球谐分析建立了740阶次的EMM模型,并用MATLAB实现了EMM模型(2000~2019年)在地球上任意地磁场7要素的计算,将软件计算值与NOAA公布的模型的计算结果进行误差对比分析,实现了等值线图的绘制,便于EMM模型的推广和应用。
1 计算理论EMM2015是EMM最新模型,其有效计算时间为2000-01-01~2019-12-31。该模型的主磁场部分来源于波兹坦地磁场模型(potsdam magnetic model of the earth,POMME),为POMME2~POMME10模型的前15阶,岩石圈磁场部分则来源于NGDC-720模型[10]。NGDC-720模型是Maus[11]使用椭球谐分析方法在综合利用磁场数据的基础上增加地磁异常网格(earth magnetic anomaly grid, EMAG)系列中的EMAG2和综合磁场(magnetic field,MF)系列中的MF6模型长波长的部分进行研制,展开的截断阶次是720,为了与标准地磁软件兼容,该模型转为球谐的表达形式,其展开截断阶次是740,相应地EMM2015模型的球谐形式的截断阶次应为740,但是国内文献使用的是截断阶次为720[9],导致模型的分辨率较低,因此,本文主要研究740阶的EMM模型。
EMM模型有7个要素,分别是总强度Fe、水平分量He、磁偏角De、磁倾角Ie、北向分量Xe,东向分量Ye、垂直分量Ze。其中,Xe、Ye、Ze在地心坐标系中表示为:
| $ \left\{ \begin{array}{l} {X_e} = \sum\limits_{n = 1}^{740} {\sum\limits_{m = 0}^n {{{\left( {\frac{{{R_e}}}{r}} \right)}^{n + 2}}} } \left( {g_n^m\cos (m\lambda ) + } \right.\\ \left. {h_n^m\sin (m\lambda )} \right)\frac{{\rm{d}}}{{{\rm{d}}\theta }}P_n^m(\cos \theta )\\ {Y_e} = \sum\limits_{n = 1}^{740} {\sum\limits_{m = 0}^n {{{\left( {\frac{{{R_e}}}{r}} \right)}^{n + 2}}} } \frac{m}{{\sin \theta }}\left( {g_n^m\sin (m\lambda ) - } \right.\\ \left. {h_n^m\cos (m\lambda )} \right)P_n^m(\cos \theta )\\ {Z_e} = \sum\limits_{n = 1}^{740} {\sum\limits_{m = 0}^n {(n + 1)} } {\left( {\frac{{{R_e}}}{r}} \right)^{n + 2}}\left( {g_n^m\cos (m\lambda ) + } \right.\\ \left. {h_n^m\sin (m\lambda )} \right)P_n^m(\cos \theta ) \end{array} \right. $ | (1) |
式中,Re为WGS-84椭球的平均半径,约为6 371.2km;(λ,θ,r)表示的地磁场在地心坐标系的位置,其中,θ为其地心余纬度,λ为其从格林威治起算的经度,r为其至参考圆球球心的径向距离;Pnm(cosθ)为Schmidt半标准化缔合勒让德函数,n、m分别为球谐分析函数的阶与次;gnm、hnm为球谐分析系数。
推导得到的Pnm(cosθ)和
| $ \left\{ {\begin{array}{*{20}{l}} {P_n^m(\cos \theta ) = \frac{1}{n}\sqrt {1 - \frac{1}{{2n}}} \sin \theta P_{n - 1}^{m - 1}(\cos \theta ), n = m}\\ {\frac{d}{{d\theta }}P_n^m(\cos \theta ) = \sqrt {1 - \frac{1}{{2n}}} \left( {\sin \theta \frac{d}{{d\theta }}P_{n - 1}^{m - 1}(\cos \theta ) + \frac{{\cos \theta }}{n}P_{n - 1}^{m - 1}(\cos \theta )} \right), n = m}\\ {P_n^m(\cos \theta ) = \frac{{(2n - 1)\cos \theta }}{{n\sqrt {{n^2} - {m^2}} }}P_{n - 1}^m(\cos \theta ) - \frac{{\sqrt {{{(n - 1)}^2} - {m^2}} }}{{(n - 1)\sqrt {{n^2} - {m^2}} }}P_{n - 2}^m(\cos \theta ), n \ne m}\\ {\frac{d}{{d\theta }}P_n^m(\cos \theta ) = \frac{{2n - 1}}{{\sqrt {{n^2} - {m^2}} }}\left( {\cos \theta \frac{d}{{d\theta }}P_{n - 1}^m(\cos \theta ) - \frac{{\sin \theta }}{n}P_{n - 1}^m(\cos \theta )} \right) - \frac{{\sqrt {{{(n - 1)}^2} - {m^2}} }}{{\sqrt {{n^2} - {m^2}} }}\frac{d}{{d\theta }}P_{n - 2}^m(\cos \theta ), n \ne m} \end{array}} \right. $ | (2) |
该递推式(2)相关的初始值为:
| $ \left\{ {\begin{array}{*{20}{l}} {P_1^0(\cos \theta ) = 2\cos \theta , P_1^1(\cos \theta ) = 2\sin \theta }\\ {P_2^0(\cos \theta ) = 4.5{{\cos }^2}\theta - 1.5}\\ {P_2^1(\cos \theta ) = 3\sqrt 3 \sin \theta \cos \theta }\\ {\frac{{\rm{d}}}{{{\rm{d}}\theta }}P_1^0(\cos \theta ) = - \sin \theta , \frac{{\rm{d}}}{{{\rm{d}}\theta }}P_1^1(\cos \theta ) = \cos \theta }\\ {\frac{{\rm{d}}}{{{\rm{d}}\theta }}P_2^0(\cos \theta ) = - 3\sin \theta \cos \theta }\\ {\frac{{\rm{d}}}{{{\rm{d}}\theta }}P_2^1(\cos \theta ) = \sqrt 3 \left( {{{\cos }^2}\theta - {{\sin }^2}\theta } \right)} \end{array}} \right. $ |
主磁场部分的球谐分析系数每天都不一样,由于岩石圈部分的地磁场变化极小,具有较高的稳定性,因而该部分的系数保持不变,具体系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {g_n^m = g_n^m(T) + G_n^m(T)(t - T)n \le 15}\\ {h_n^m = h_n^m(T) + H_n^m(T)(t - T)n \le 15} \end{array}} \right. $ | (3) |
式中,t为计算的日期(当t在2000-01-01~2015-12-31,T为t所在的年份;当t在2016-01-01~2019-12-31,T等于2015年);Hnm(T)、Gnm(T)为长期变化系数。
2 计算思路1) 将大地坐标转换为地心坐标。通常需要计算的空间位置是基于大地坐标系的,而EMM是基于地心坐标系下的模型,需要将大地坐标系(λ,φ′,h)转为地心坐标系(λ,θ,r),两者变换的示意图如图 1所示,A、B分别为椭球的长半轴和短半轴,A=6 378.137 km,B=6 356.752 314 2 km。
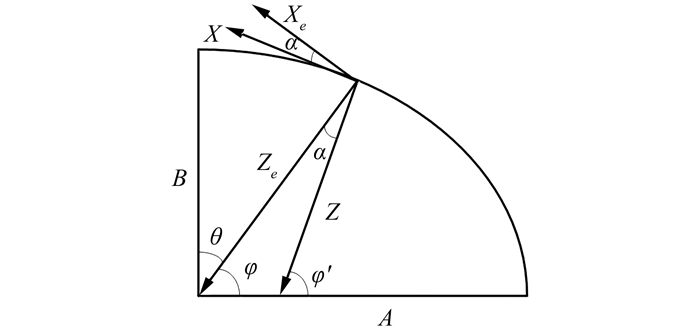 |
| 图 1 大地坐标系和地心坐标系下磁场分量示意图 Fig.1 Magnetic Field Component Diagram in Geodetic and Geocentric Coordinate System |
大地坐标系转为地心坐标系公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {P = \sqrt {{A^2}{{\cos }^2}{\varphi ^\prime } + {B^2}{{\sin }^2}\varphi '} }\\ {r = \sqrt {h(h + 2P) + \frac{{{A^4}{{\cos }^2}{\varphi ^\prime } + {B^4}{{\sin }^2}{\varphi ^\prime }}}{{{P^2}}}} }\\ {\cos \alpha = \frac{{h + P}}{r}, \sin \alpha = \frac{{\left( {{A^2} - {B^2}} \right)\sin {\varphi ^\prime }\cos {\varphi ^\prime }}}{{rP}}}\\ {\cos \theta = \sin {\varphi ^\prime }\cos \alpha - \cos {\varphi ^\prime }\sin \alpha }\\ {\sin \theta = \cos {\varphi ^\prime }\cos \alpha + \sin {\varphi ^\prime }\sin \alpha } \end{array}} \right. $ | (4) |
2) 由三角函数两角和公式计算可得cos(mλ)、sin(mλ),再根据式(1)~式(3)求得地心坐标下的Xe、Ye、Ze。cos(mλ)、sin(mλ)为:
| $ \left\{ {\begin{array}{*{20}{l}} {\cos (m\lambda ) = \cos ((m - 1)\lambda )\cos \lambda - \sin ((m - 1)\lambda )\sin \lambda }\\ {\sin (m\lambda ) = \sin ((m - 1)\lambda )\cos \lambda + \cos ((m - 1)\lambda )\sin \lambda } \end{array}} \right. $ | (5) |
3) 根据X=Xecosα+Zesinα,Y=Ye,Z=Zecosα-Xesinα求得大地坐标系下的X、Y、Z[7]。
4) 根据
1) 程序实现。使用MATLAB中的GUI进行界面设计,实现的主要功能为:①计算地球任意点的地磁场7要素,为了满足不同经纬度表示方法,该部分有两种输入格式,一种是以度为单位输入,另外一种是度分秒格式输入;②绘制7要素EMM(2000~2019年)的等值线图如图 2所示, 图 2中,白色部分是由于等值线密集造成的。
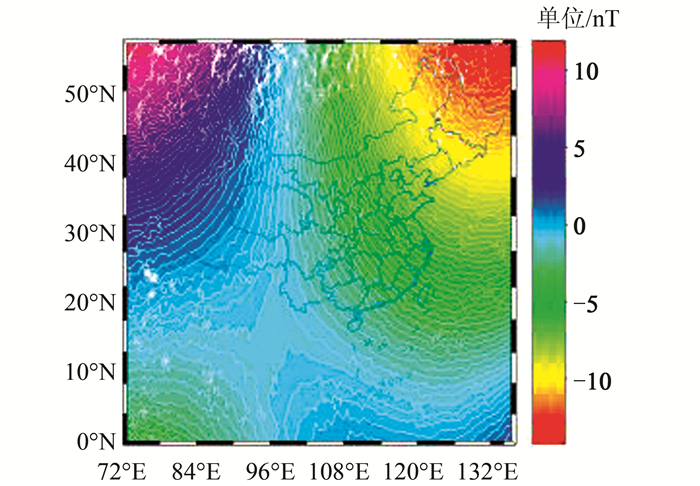 |
| 图 2 等值线图 Fig.2 Contour Mapping |
2) 误差分析。为了检验自编的EMM-740模型的准确度,以NOAA公布的模型的运行数据为标准值,比较自编软件的地磁场数据计算值与标准值的偏差以及720阶的EMM与标准值的偏差。鉴于EMM是全球模型,应在全球范围内进行自编软件的偏差分析,仿真条件设定为:时间(2013-06-05),纬度范围(80°S~80°N),经度范围(180°W~180°E), 高度(0 m),根据图 3取16个不同经纬度的点并按照标注的序号进行编号,740阶和720阶的EMM模型的7要素的计算值与标准值的偏差值如表 1所示。
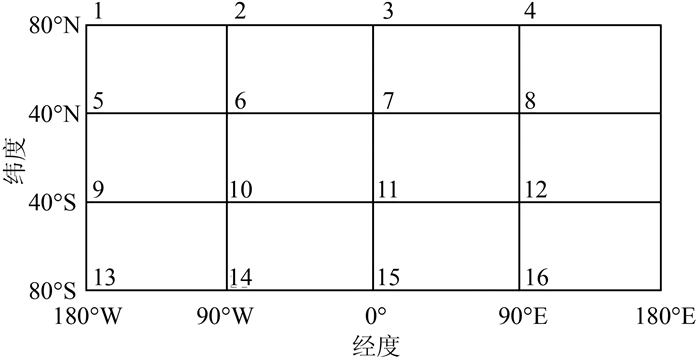 |
| 图 3 取点示意图 Fig.3 Diagram of Taking the Points |
| 表 1 高度为0 m时误差对比分析 Tab.1 Error Comparison Analysis When the Height with 0 m |
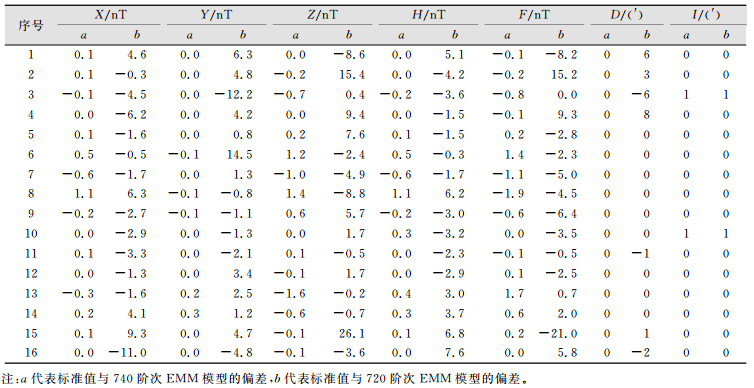 |
从表 1可以看出,用自编EMM-740软件计算的各元素值与NOAA的计算的元素值偏差较小,元素X、Y、Z、H、F、D、I的偏差最大值分别为1.1 nT、0.3 nT、1.4 nT、1.1 nT、1.7 nT、0′、1′,最小值分别为-0.6 nT、-0.1 nT、-1.6 nT、-0.6 nT、-1.9 nT、0′、0′,计算的均值分别为0.1 nT、0.0 nT、-0.1 nT、0.1 nT、0.0 nT、0′、0′;用自编的720阶的EMM软件计算的各元素值与NOAA的计算的元素值偏差较大,元素X、Y、Z、H、F、D、I的偏差最大值分别为9.3 nT、14.5 nT、26.1 nT、7.6 nT、15.2 nT、6′、1′,最小值分别为-11.0 nT、-12.2 nT、-8.8 nT、-4.2 nT、-21.0 nT、-2′、-1′,计算的均值分别约为-0.8 nT、1.3 nT、2.4 nT、0.5 nT、-1.5 nT、1′、0′。元素i的均方根偏差(root mean square, RMSE)为:
| $ {i_{{\rm{RMSE}}}} = \sqrt {\sum\limits_{n = 1}^{16} {\Delta _n^2} /(n - 1)} $ | (6) |
式中,i为7要素中的任一元素;Δn为该元素的对应的第n个偏差值。
根据式(6)可计算出EMM-740的各个元素的RMSE分别为0.37 nT、0.10 nT、0.74 nT、0.39 nT、0.86 nT、0.0′、0.4′,而720阶的EMM的各个元素的RMSE分别为5.04 nT、5.85 nT、9.30 nT、4.18 nT、8.09 nT、3.2′、0.4′。可见,740阶的EMM模型比720阶的计算的精度约提高了3倍。
4 结束语高精度地磁场模型的程序及可视化的实现可以快速、准确地获得测点地磁场值,丰富磁力仪的软硬件功能。目前,大多数程序及可视化的实现都是针对IGRF模型的,而针对EMM模型的计算和可视化的实现的研究较少,同时还存在720阶和740阶的概念混淆的情况,另外,程序的精度也较低。本文结合实际背景,考虑了地磁场7要素,给出了EMM模型的计算步骤,实现了基于球谐分析的740阶次EMM模型的程序,并将其计算结果和720阶的EMM程序的计算结果与NOAA公布的EMM2015模型的计算结果进行了比较,本文提出的模型实现方法有较高的精度,有利于后续的研究和实验。
| [1] |
刘磊, 姚宜斌, 孔建. 尼泊尔地震震前电离层异常变化特征[J]. 测绘地理信息, 2016, 41(4): 13-17. |
| [2] |
Zhao Ta, Chen Yuwei, Zhou Zhijian, et al. Research on Three-Component Geomagnetic Field Differential Measurement Method for Underwater Vehicle[J]. International Journal of Multimedia and Ubiquitous Engineering, 2016, 11(2): 89-98. DOI:10.14257/ijmue.2016.11.2.11 |
| [3] |
Canciani A, Raquet J. Airborne Magnetic Anomaly Navigation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 67-80. DOI:10.1109/TAES.2017.2649238 |
| [4] |
杨业, 谢益炳, 陆亚峰, 等. 基于陆态网数据低阶球谐函数电离层区域建模[J]. 测绘地理信息, 2015, 40(3): 45-47. |
| [5] |
柴松均, 陈曙东, 张爽. 国际地磁参考场的计算与软件实现[J]. 吉林大学学报(信息科学版), 2015, 33(3): 280-285. DOI:10.3969/j.issn.1671-5896.2015.03.010 |
| [6] |
高德章. 国际地磁参考场及其计算[J]. 海洋石油, 1999, 19(3): 34-42. |
| [7] |
肖胜红, 边少锋, 黄晓颖. 地磁场模型计算软件的可视化设计与实现[J]. 测绘信息与工程, 2009, 34(5): 18-20. |
| [8] |
冯春. Matlab实现IGRF国际地磁参考场模型的计算[J]. 内蒙古石油化工, 2014, 40(12): 43-46. DOI:10.3969/j.issn.1006-7981.2014.12.018 |
| [9] |
刘元元, 张金生, 孙渊, 等. 世界地磁场模型EMM2010及其应用[J]. 地球物理学进展, 2012, 27(5): 1 939-1 946. |
| [10] |
冯丽丽, 王粲, 陈斌, 等. 基于MF6, EMM2010和CGRF2010模型的中国大陆地壳磁异常特征[J]. 地震学报, 2015, 37(6): 997-1 010. |
| [11] |
Maus S. An Ellipsoidal Harmonic Representation of Earth's Lithospheric Magnetic Field to Degree and Order 720[J]. Geochemistry, Geophysics, Geosystems, 2010, 11(6). DOI:10.1029/2010GC003026 |
 2019, Vol. 44
2019, Vol. 44

