| Geohash编码的周边查找算法优化 | [PDF全文] |
周边查找又称周边搜索,是指在已知的地理位置上查找满足一定空间和属性条件的地理要素的过程[1]。常见的应用如手机应用程序提供的周边查找功能,已知手机使用者的位置数据,通过检索海量地理要素来发现附近的服务设施(发现外卖、美食、景点、酒店等),又如快速查询自然灾害发生地周边的应急响应物资[2]。从GIS的角度来看,周边查找就是一个空间分析过程,即对于一个圆形的面要素与一个点集合进行空间相交分析,相交的结果是圆域内部的点集合。在算法实现上,需要计算点集合中的每个点到圆心的距离,当点集合中的点要素数量巨大(十万或百万级以上)时,算法耗时很长,难以满足应用上的实时性需求。随着大数据时代到来,数据密集型问题导致计算模型和分析方法发生新的变化[3, 4]。为了减少检索用时,对点集合构造合适的空间索引并改造搜索算法是必要的,以Geohash为基础的地理网格索引与周边查找算法就是其中之一[5]。
本文简要阐述基于Geohash的网格索引机制与周边查找算法的一般流程,指出其中存在的问题并提出优化的方向,阐述了优化后的周边查找算法流程,通过实验比较了优化前后的算法效率。
1 Geohash与周边查找算法Geohash是一种基于规则网格的地理编码方式,与Morton码具有一一对应的关系。通过对全球地表空间的经纬度进行二分法划分获得01码序列,再交叉合并(经度在前)成为Morton码。Morton码把地表分成2n行、2n列的规则网格(n为划分层次),任意网格对应唯一Morton码[6-8]。当n很大时,码序列很长,对这种码序列进行Base32编码压缩的方法称为Geohash,Geohash使Morton码序长度压缩为原来的20%。Geohash和Morton码具有类似特性[5]:网格唯一性、空间递归性、编码一维性。Geohash以及Morton码的编码方式决定了网格的空间遍历顺序,可由Z字形的Peano型空间遍历曲线表示。Geohash的特点使其在海量数据的组织方面发挥出巨大的作用[9]。
基于Geohash规则网格索引的周边查找算法示意图如图 1所示,具体步骤是:①根据搜索半径确定Geohash编码的前缀长度(判断准则:前缀长度为m时,对应Geohash网格的较小边长大于圆心所在地理位置的搜索半径转换成的经纬度跨度,且此时m是所有满足条件的最大值),计算出搜索中心所在的父级网格编码,也就是Geohash前缀编码;②为了防止一些在父级空间外且靠近其边界的点被遗漏,需要计算出与父级网格相邻的8个父级网格的Geohash前缀[1, 5, 10, 11];③对这9个Geohash前缀网格分别遍历基本Geohash空间,并遍历每个空间内的兴趣点,这一步操作通过在数据库表中使用前缀匹配查询来完成;④计算遍历的每个兴趣点到搜索中心的距离,将满足条件的兴趣点加入到结果,最后反馈给用户。
从上述的算法流程来看,存在这样问题:①计算中间以及周围8个邻域Geohash前缀的过程有可能导致一部分原本不在搜索圆域内的区域进入到后续的计算步骤中(如图 1(b)中下方3个前缀网格),这样会额外增加不必要的分析时间;②在Geohash前缀网格中遍历出的Geohash基本网格也有可能完全与搜索圆域相离(如图 1(c)中的最左列、最右列以及第1行第2列和第1行第5列的基本网格),这部分网格中的点也没有必要进行后续计算;③一些基本网格完全在搜索圆域内部(如图 1(c)中的第3行第3列和第3行第4列的基本网格),那么其中的点也必然在搜索圆域内,这部分兴趣点不再计算与搜索域圆心的距离。所以,在算法流程上可以通过优化来预先保留合格网格、剔除不合格网格,从空间关系上看,只计算与圆域边界相交的部分网格中的兴趣点,通过这样的预处理会有效地减少最终计算距离的兴趣点数量,以图 1为例,计算距离的兴趣点个数从44个减少为16个。
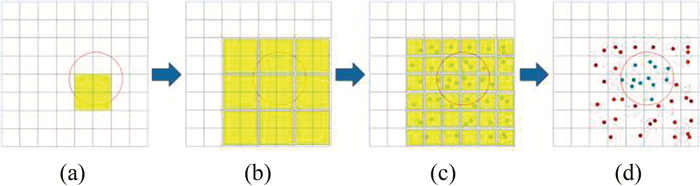 |
| 图 1 常规方法的步骤 Fig.1 Process of Common Algorithm |
2 优化算法的设计
本文的周边查找算法针对上述3个问题对原算法进行了适当的改进。总体来讲,增加了外包盒过滤和搜索圆过滤的优化方法。优化算法的步骤示意图如图 2所示。
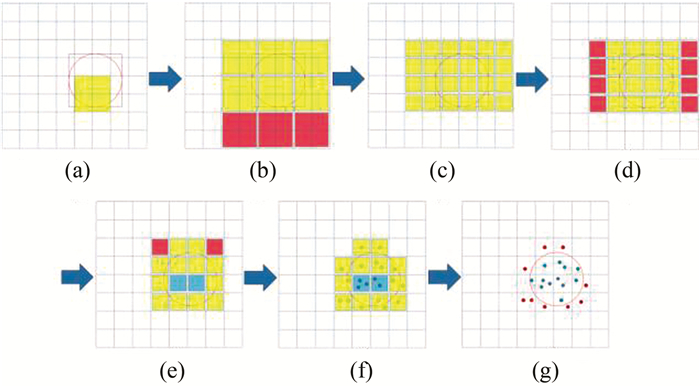 |
| 图 2 优化方法的步骤 Fig.2 Process of Optimization Algorithm |
优化算法的具体步骤为:①根据搜索半径确定Geohash编码的前缀长度,计算出搜索中心所在的父级网格的Geohash前缀编码与地理外包盒;②计算搜索半径对应的经纬度跨度,结合圆心地理坐标判断圆域外包盒是否跨越中心前缀网格的边界,只对跨越边界的一侧计算相邻前缀网格编码;③对中心网格和跨越的邻域前缀网格计算其包含的Geohash基本网格的编码与地理外包盒;④基本网格的地理外包盒与圆域外包盒进行相交分析,标记相离的基本网格;⑤删除相离的基本网格,对留下的基本网格与圆域进行相交分析,并分别标记相离和内含的基本网格; ⑥删除相离的基本网格,对于内含的基本网格通过表查询取出网格中的兴趣点直接加入结果,对于待定基本网格通过表查询取出待定兴趣点,计算待定兴趣点到搜索圆心的距离,保留距离小于搜索半径的兴趣点; ⑦将步骤⑥中的兴趣点添加到结果中,与内含点一起输出。从代码的最终实现上来看,优化算法的步骤可以适当地合并,如计算邻域前缀编码与计算外包盒的代码进行合并;去掉标记过程,先计算外包盒,在判断相离的同时直接剔除而不必等待每个网格分析完毕再一起操作。总之,要根据不同编程语言环境提供的数据库访问接口以最方便的途径来决定代码的最终实现。
关于两点间地表距离的计算方法选择问题,基于经纬度的地理参考系统提供对位置的精确描述,同时允许对位置点间的长度进行计算,在大地测量学中参考椭球体上的两个地理点的距离计算常采取贝塞尔大地主题反算,计算过程包括:计算辅助函数、通过迭代趋近来计算正球面上两点距离、将正球面上距离变换到椭球上得到大地线长度。贝塞尔大地主题反算的结果精度高但是过程繁琐,反复使用此方法时耗时很多[12]。为保证计算速度,本文采用Haversine大圆距离公式计算球面距离,并在搜索半径上增加误差来保证搜索准确性。
另外,Geohash编码后是以字符串的形式进行保存的,使用Geohash实现周边查找功能要求数据库具有索引字符串的能力,所以需要考虑数据库的选取。在这个方面,基于文档、对词汇进行分割索引的非关系型数据库(如MongoDB)或搜索引擎(如Elasticsearch)已经实现了对Geohash字符串的索引,所以优先选择这类数据库存储数据[13, 14]。如果选择使用那些不具备对字符串进行索引能力的对象关系型数据库,则需要在具体实现上稍作修改:将Geohash字符串用Morton码整数来代替并对Morton码设定一个整数索引。由于Geohash与Morton码的一一对应关系,Geohash的前缀会被映射为一个Morton码整数闭区间,前缀查询就变换为一个整数范围查询,利用B树或其他索引来加快检索[6]。如长度是10的Morton码的前缀为0110,那么满足该前缀的Morton码会在0110000000和0110111111之间变化,前缀就映射成十进制值闭区间[384, 447],其中每个整数都对应一个基本网格Morton码,也就对应唯一的Geohash编码。结构化查询语言(structured query language, SQL)查询的条件就是Morton码整数在闭区间[384, 447]内。
3 实验测试与分析在实验前需要做一些准备工作:①数据源方面,被测试兴趣点包含地名、地址、WGS84坐标位置信息。②数据存储方面,采用开源搜索引擎Elasticsearch存储兴趣点数据,对每个兴趣点存储所在的Geohash基本网格的编码,并对Geohash编码构建字符串索引。Geohash字符串的长度设置为6,对应二进制位长度为30,即对全球区域的经纬度分别进行15次二分法划分。在这种划分情况下,中纬度地区的Geohash基本网格边长尺寸在600 m左右,网格内兴趣点约有上百个,同时网格数量不会太多,是一个对局部地区划分程度合适的长度。③算法的实现方面,两种不同的周边查找算法以Elasticsearch工程的Java源代码为基础进行修改实现,通过Elasticsearch的工程框架提供的应用程序编程接口Java API(application programming interface)对两种周边查找算法进行调用。④测试程序设计方面,采用客户端/服务器(client/server,C/S)架构,服务端运行Elasticsearch,客户端为一个窗体形式的测试程序,通过调用Elasticsearch提供的Java API实现向服务端提交周边查找的请求,测试程序的同时负责记录下从提交请求到接收到返回结果的时间。
测试周边查找算法速度的实验遵循了以下原则:①对每个周边查找的中心都进行了多次实验,目的是削弱硬件的不稳定性;②实验的周边查找中心从兴趣点中选出,避免查找圆中没有兴趣点;③实验随机选取多个兴趣点作为周边查找中心,目的是削弱所选取点的地域聚集特性对结果的影响。
实验1测试了两种算法在多个城市的用时。测试数据来源于国内的地名地址网站,包含北京、武汉、唐山3个城市的兴趣点共16万个。实验在各城市的兴趣点中随机选取了100个点分别作为周边查找圆心,对每个点设定不同半径(500 m、1 km、2 km、5 km、10 km)且重复查询10次,得到两种算法的用时比较,如表 1所示。
| 表 1 两种方法在3个城市中的用时比较 Tab.1 Time Comparison of Two Methods in Three Cities |
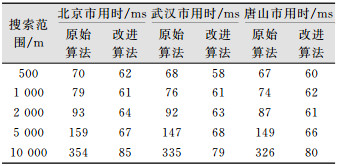 |
实验2测试了对于单个城市在兴趣点密度不同的条件下两种算法的用时,用于研究点密度对于算法效率的影响。测试数据来自于开放街道地图(open street map,OSM),是武汉市的40万个兴趣点数据,利用点稀释方法将数据提炼成4个层级(5万、10万、20万、40万),保证每层点分布特征一致。实验查询范围是5 km,每一层随机抽样100个点,单点重复查询10次,记录下两种算法的用时比较,如表 2所示。
| 表 2 不同数据量下算法用时比较 Tab.2 Time Comparison of Two Methods Under Different Amounts of Data |
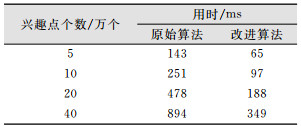 |
从实验1(表 1)的结果可以看出,原始算法的耗时随着搜索范围的增大而增大,且时间增长幅度远大于改进算法,当搜索范围达到2 km的查找耗时就已经接近100 ms,当范围达到5 km时耗时远远超出了100 ms。而改进算法的耗时即使在搜索范围达到10 km时依然保持在100 ms以内,且在5 km范围内的耗时都稳定在了较小的值。充分说明优化算法中提前过滤掉不合格网格,直接保留合格网格的做法是合理的。同时,不同城市的实验结果也说明算法具备普遍适用性。另外,改进算法用时在范围从500 m提高到1 km出现的轻微下降可能与样本的随机性有关。从实验2(表 2)的结果可以看出,随着数据密度的增加,两种算法的用时都有增加。当数据密度成倍增长时,两种算法的用时基本上也在成倍增长。由于改进算法在最小层级时的计算时间远小于原始算法,所以在数据量经过多次翻倍后其优势变得更加明显。
4 结束语本文提出了优化基于Geohash实现周边查找算法的方法,可以大幅度提高周边查找的效率。优化算法中的某些步骤还有更好的方案可以替换,如从Geohash前缀网格遍历基本网格的过程可以改为逐级遍历网格,并对不同层次的前缀网格进行空间过滤,可以更早剔除掉不合格网格。另外,由于兴趣点数据带有社会属性,空间分布具有聚集特性,所以算法性能还需要更多的实际数据来检测。周边查找用时与地理要素空间分布特性的关系也需要作为一个课题来研究,用于设计出更加合理的算法。
| [1] |
赵雨琪, 牟乃夏, 祝帅兵, 等. 基于GeoHash算法的周边查询应用研究[J]. 软件导刊, 2016, 15(6): 16-18. DOI:10.3969/j.issn.1672-7800.2016.06.008 |
| [2] |
丁娟, 马犇, 何琳, 等. 基于Arc Engine的震中周边应急资源信息查询系统[J]. 中国科技信息, 2016(8): 59-60. DOI:10.3969/j.issn.1001-8972.2016.08.018 |
| [3] |
艾廷华. 大数据驱动下的地图学发展[J]. 测绘地理信息, 2016, 41(2): 1-7. |
| [4] |
边馥苓, 杜江毅, 孟小亮. 时空大数据处理的需求、应用与挑战[J]. 测绘地理信息, 2016, 41(6): 1-4. |
| [5] |
金安, 程承旗, 宋树华, 等. 基于Geohash的面数据区域查询[J]. 地理与地理信息科学, 2013, 29(5): 31-35. |
| [6] |
易显天, 徐展, 郭承军, 等. 基于Patricia树的空间索引结构[J]. 计算机工程, 2015, 41(12): 69-74. DOI:10.3969/j.issn.1000-3428.2015.12.014 |
| [7] |
孟庆武, 王文福, 孟露, 等. 基于Morton码的一种动态二维游程压缩编码方法[J]. 测绘科学, 2011, 36(3): 202-203. |
| [8] |
张天蛟, 严泰来, 王海蛟, 等. 基于Morton码的土地空间网格数据组织与检索[J]. 农业工程学报, 2013, 29(S1): 235-243. |
| [9] |
向隆刚, 王德浩, 龚健雅. 大规模轨迹数据的Geohash编码组织及高效范围查询[J]. 武汉大学学报·信息科学版, 2017, 42(1): 21-27. |
| [10] |
王翔, 杨国东. 基于Geohash的出租车汽车轨迹的存储与应用研究[J]. 科技资讯, 2015(35): 69-71. |
| [11] |
杜景林, 蔡苏鹏. 基于Geohash的人工影响天气气象预警系统设计[J]. 计算机应用与软件, 2015, 32(8): 88-93. DOI:10.3969/j.issn.1000-386x.2015.08.021 |
| [12] |
孔祥元, 郭际明, 刘宗泉. 大地测量学基础[M]. 2版. 武汉: 武汉大学出版社, 2010.
|
| [13] |
毛法尧. B树分析[J]. 计算机工程与应用, 1995(2): 22-24. |
| [14] |
唐宏, 盛业华, 杜培军. 基于十进制Morton码的线性四叉树动态编码方法研究[J]. 江苏测绘, 1999, 22(3): 11-13. |
 2019, Vol. 44
2019, Vol. 44

