| 长距离跨海高程传递测量方法研究与工程实践 |
2. 武汉大学测绘学院,湖北 武汉,430079;
3. 61234部队,新疆 乌鲁木齐,830006;
4. 武警湖北省总队后勤部,湖北 武汉,430070
2. School of Geodesy and Geomatics, Wuhan University, Wuhan, 430079, China;
3. 61234 Troops, Urumqi, 830006, China;
4. Hubei Provincial Armed Police Corps Logistics Department, Wuhan, 430070, China
随着国民经济发展和国家综合实力提高,我国沿海岛屿的重要性日益突出。为开发海洋资源、维护海洋权益,迫切需要确定海岛的地理位置和空间坐标。跨海高程传递是建立海陆一体化大地高程基准的一种主要手段,目前国内跨海正常高程传递采用的方法主要有测距三角高程、验潮法和GPS水准法。测距三角高程法是目前较常见的海岛高程基准测量方法,其误差来源主要有测距误差、测角误差、地球曲率及大气折光差、仪器和标志高量测误差。本文通过对三角高程测量的基本原理分析、误差公式推导并结合某处跨海高程试验,对长距离跨海高程传递测量进行了方法研究、精度分析和工程实践。
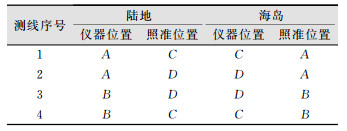
1 跨海高程传递测量方法和精度分析 1.1 高程传递测量方法如图 1所示,分别在两岸地形地貌相似、高差不大的陆地和海岛岸边建立A、B、C、D 4个观测墩,观测墩上带强制归心装置并适合GNSS测量。测量步骤为:①采用几何水准的方法联测A、B两点的高程, 测出C、D间的高差;②4个观测墩进行同步GNSS观测,精确测定AC、AD、BC、BD的基线长度;③两岸各采用一台型号相同的全站仪进行同步对向垂直角观测,其观测顺序如表 1所示,完成测线AC、AD、BD、BC对向观测为一个完整的光段(每条测线观测16个测回),总的光段数N=4×S(S为跨海距离,单位为km),当观测光段数为总光段数N的一半时,两岸全站仪和观测员进行对调观测;④以测线斜距定权,进行条件平差计算C、D两点的高程。
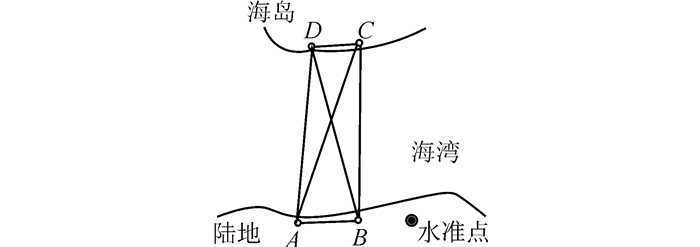 |
| 图 1 跨海高程传递测量示意图 Figure 1 Measurement Schematic of Cross-Sea Elevation Transmission Surveying |
| 表 1 同步对向观测测线观测顺序 Table 1 Baseline Observation Sequence of Synchronization Subtend Observation |
 |
1.2 三角高程对向观测精度分析
三角高程测量是通过观测两点间的水平距离和高度角运用三角公式来计算两点间的高差。如图 2所示,D和S为地面A、B两点间实测的水平距离和斜距,
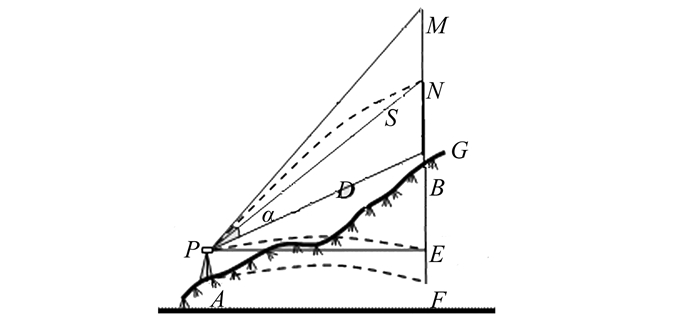 |
| 图 2 三角高程测量球气差改正示意图 Figure 2 Earth Curvature and Refraction Effect of Trigonometric Leveling |
由于大气折光差的影响,自目标N的光线NP进入仪器的望远镜,而望远镜的视准轴却位于弧线PN的切线PM上,MN即为大气折光对三角高程的影响。
| $ {{h}_{AB}}=D\tan \alpha +i-v+(1-k){{D}^{2}}/(2R) $ | (1) |
式中,R为地球半径;k为大气折光系数。
将式(1)进行微分,由误差传播律整理可得:
| $ \begin{align} & m_{_{{{h}_{AB}}}}^{2}=\frac{{{D}^{2}}}{{{\cos }^{4}}\alpha \cdot {{\rho }^{2}}}m_{\alpha }^{2}+\left( {{\tan }^{2}}\alpha +\frac{(1+{{k}^{2}})}{{{R}^{2}}}{{D}^{2}} \right)\cdot m_{D}^{2}+ \\ & \ \ \ \ \frac{{{D}^{4}}m_{k}^{2}}{4{{R}^{2}}}+m_{i}^{2}+m_{v}^{2} \\ \end{align} $ | (2) |
式中, ρ=206 265″; R=6 362 732 m。
由式(2)可知,影响三角高程测量精度的主要因素有以下几点:
1) α的误差。作业采用LEICA TM5100电子全站仪,测角中误差0.5″。跨海场地选建时,两岸的高差不大,跨海视线垂直角在1°以内,取D=7 000 m,α=1°,mα=0.5″,可得式(2)中等号右边第1项为288 mm2。
2) D的误差。由D=Scosα可得:
| $ m_{D}^{2}={{\cos }^{2}}\alpha \cdot m_{S}^{2}+{{\sin }^{2}}m_{\alpha }^{2}/{{\rho }^{2}} $ | (3) |
式(3)右边第2项是一个微小量,可忽略不计,故mD2<mS2,作业采用的TOPCON NET-G3A接收机标称精度为3 mm+0.5×10-6,取mS=6 mm,根据文献[4]取k=0.15,可得式(2)中右边第2项为45 mm2。
3) k的误差。折光系数k主要取决于温度梯度和大气密度。一般情况下早晚变化较大,中午附近比较稳定,阴天和夜间最好,应选择最佳观测时间。文献[4]表明,折光系数k的中误差约为±0.03~±0.05。取mk=±0.04,D=7 000 m,则式(2)右边第3项为23 668 mm2。
4) i和v的影响。跨海观测墩上安置强制归心装置,用特制的精密量高尺量取仪器高和照准标志,量高尺标称精度为0.1 mm。
将上述各项误差影响值代入式(2)可得:
| $ m_{_{{h_{AB}}}}^2 = (288 + 45 + 23668 + 0.1 + 0.1)m{m^2} $ | (4) |
由式(4)可知,大气折光系数k对mhAB的影响最大,远远超过其他误差的影响。由文献[4]可知,当D>600 m后,k的影响会急剧增大,三角高程测量的垂直折光只涉及大气层底部,在温度、湿度、气压条件变化很小的情况下,k值变化较小,气象条件相同的测站两端折光影响大致相等,短距离同步对向观测能基本消除折光差,但在实际作业条件下,要使测站和照准目标之间完全对称,使得对向观测所产生的折光角完全相等,只是一种非常理想的状态,观测环境的不完全对称造成的大气折光差是长距离跨海高程传递测量误差的主要来源。因此,基于测距三角高程的跨海高程传递采取完全同步的观测模式,严密执行上午、下午、晚上不同时段,完成规定的观测光段,能有效减弱垂直折光影响,大大提高结果精度。
2 测量工程实践及分析依前文所述观测方法,在某处按图 1所示大地四边形结构布设观测场地,用4台TOPCON NET-G3A接收机进行基线测量,其中基线测量同步GPS观测23.5 h,获得AC、AD、BD和BC的长度。两台LEICA TM5100A全站仪进行垂直角对向观测,垂直角观测光段数为40个,历时15 d。
2.1 GPS基线测量成果分析空间距离获取采用同步GPS观测,高度截止角设置为15°,采样率30 s,4台接收机同步观测23.5 h,采用自由网平差,基线解算结果见表 2。
| 表 2 基线解算结果 Table 2 Result of Baseline Calculation |
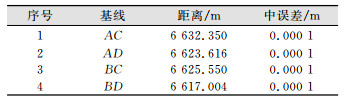 |
由于所选择的4个跨海观测点周围地势开阔,观测条件好,静态观测时间较长,相对测量精度极高,完全满足公式(3)中S的精度要求。
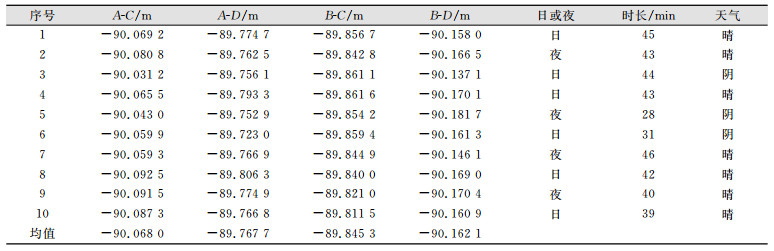
2.2 三角高程测量对向观测成果分析本次试验所测40个光段中,取前10个光段数据进行分析,表 3为各条基线对向往返观测高差之差的平均值(往测高差为负,返测高差为正),表 4为各条基线对向观测高差的不符值(同步对向往、返观测高差之和)。
| 表 3 跨海高程传递测量基线对向观测高差平均值 Table 3 Average of Baseline Subtend Observation Elevation Difference in Cross-Sea Elevation Transmission Surveying |
 |
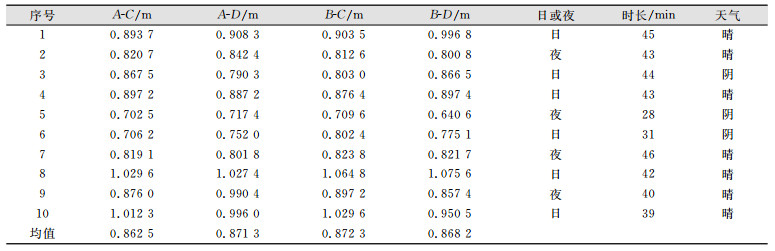
| 表 4 跨海高程传递测量基线对向观测高差不符值 Table 4 Discrepancy of Baseline Subtend Observation Elevation Difference in Cross-Sea Elevation Transmission Surveying |
 |
由表 3中可看出,夜间数据在均值附近跳动较小,明显优于白天数据;同样是白天,阴天的数据要好于晴天的数据,观测时间越短,气温变化越小,受大气折光影响越小,数据质量越好。
从表 4中可看出,各基线同步对向往返观测之和均在0.8 m附近跳动,虽然对向观测可以很好地消除地球曲率的影响,但大气折光差受温度、气压和湿度等因素的影响,未能彻底消除,只能通过同时、对向、重复的观测进行筛选,剔除数据质量较差的光段。
2.3 跨海高程传递成果分析本处跨海试验共观测40光段,采用文献[6]提供的方法,剔除光段互差和环闭合差较大的12个光段,剩余28个光段成果作为跨海高程传递的最终成果,计算跨海高程。按照条件平差的原理对数据进行严密平差,共有6个观测值,3个多余观测,组成3个条件方程,平差结果见表 5。
| 表 5 高差平差结果表 Table 5 Balancing Result of Elevation Difference |
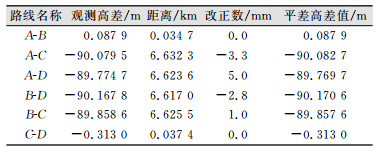 |
最后平差计算可得C点中误差为0.9 mm,D点中误差为0.9 mm,每千米高差中数中误差为0.8 mm,达到二等水准规范的精度要求。
3 结束语本次跨海高程传递测量工程实践采用GNSS精密测距和高精度全站仪进行同步对向垂直角观测相结合的方法,该方法对今后的长距离跨河、跨海三角高程测量有一定的参考意义和应用价值,根据公式(2)的精度分析和本处跨海试验结果,为提高作业精度尤其是如何控制大气折光差的影响还需采取如下措施:①跨海观测点应尽量选址在两岸地形地貌相似、高差相差不大的地方(垂直角尽量控制在1°以内),以便更好地消除大气折光差的影响;②同步对向垂直角观测应尽量选在风力温和、气温变化较小的阴天或夜间进行;③让观测速度相当、仪器操作熟练的观测员进行观测,尽量缩短同步对向观测时间。根据最后的试验数据结果表明,在一定条件下,用全站仪垂直角观测辅以GPS基线测量来代替二、三等水准进行长距离跨海三角高程测量的方法是可行的。
| [1] |
王文杰, 田丽亚, 刘立臣, 等. 中间法三角高程测量在高铁CPⅢ控制网中的应用[J].
测绘地理信息,2014,39(1) : 29–32.
Wang Wenjie, Tian Liya, Liu Lichen, et al. Application of Middle Method Trigonometric Leveling Measurement in the Transmitting CPⅢ Elevation Control Network[J]. Journal of Geomatics,2014,39(1) : 29–32. |
| [2] |
GB12897-2006.国家一、二等水准测量规范[S].北京:中国标准出版社, 2006 GB12897-2006. Code for One, Second-grade Leveling[S]. Beijing: Standards Press of China, 2006 |
| [3] |
张正禄, 邓勇, 罗长林, 等. 精密三角高程代替一等水准测量的研究[J].
武汉大学学报·信息科学版,2006,31(1) : 5–8.
Zhang Zhenglu, Deng Yong, LUO Changlin, et al. Research of Replacing First-degrade Leveling with Trigonometric Leveling[J]. Geomatics and Information Science of Wuhan University,2006,31(1) : 5–8. |
| [4] |
许国辉. 高精度EDM三角高程测量的研究[J].
测绘通报,2002,(10) : 22–24.
Xu Guohui. Research of EDM Trigonometric Leveling with High Precision[J]. Bulletin of Surveying and Mapping,2002,(10) : 22–24. |
| [5] |
方明, 武威. 跨海高程传递三角高程数据处理及质量分析[J].
海洋测绘,2012,(9) : 53–55.
Fang Ming, Wu Wei. Data Dealing and Quality Analysis of the Trigonometric Leveling over the Sea[J]. Hydrographic Surveying and Charting,2012,(9) : 53–55. |
| [6] |
李军国. 测距三角高程法在凫洲大桥跨河水准测量中的应用[J].
城市勘测,2008,(6) : 98–100.
Li Junguo. Applying Trigonometric Leveling with Distance Measurement to River-Crossing Leveling of the Fuzhou Bridge[J]. Urban Geotechnical Investigation & Surveying,2008,(6) : 98–100. |
| [7] |
邹进贵, 朱勇超, 童魁. 精密三角高程测量技术在高海拔山区的应用[J].
测绘地理信息,2013,38(6) : 6–9.
Zou Jingui, Zhu Yongchao, Tong Kui. Application of Precise Trigonometric Leveling Technology at High Altitude[J]. Journal of Geomatics,2013,38(6) : 6–9. |
 2016, Vol. 41
2016, Vol. 41

