| GPS导航卫星精密钟差的插值和预报方法研究 |
2. 北京航天宏图信息技术股份有限公司,北京,100195
2. Beijing AeroImgInfo Technology Co., Ltd., Beijing 100195, China
GPS导航卫星原子钟钟差在精密单点定位、精密轨道确定、卫星自主导航等领域具有重要作用。但是,一方面不同用户对于精密钟差的采样率要求不同;另一方面,用户在实时定位,定位定轨等方面对于实时精密钟差也存在需求,而IGS(international GPS service)发布的精密钟差存在产品采样率单一和事后延迟问题[1-4]。因此,研究不同采样率的精密钟差插值方法和短时、实时预报精密钟差具有重要实用价值。
1 利用不同插值方法对精密钟差进行插值 1.1 插值方法简述内插是改变精密钟差产品时间采样率的有效方法,目前IGS提供的钟差有15 min、5 min、30 s等采样间隔,但实际用户可能需要15 s、2 s等高采样率的产品[5]。为比较不同插值方法优缺点,本文选取线性插值(Linear)、拉格朗日插值(Lagrange)、三次样条插值(cubic spline)、埃米尔特插值(Hermite)等4种不同插值方法进行分析。
其中,线性插值和拉格朗日插值都是选取合适节点来构造多项式,线性插值可以视作低阶次的拉格朗日插值。该方法公式含义直观,计算量小,但是当选取新节点后必须重新构造公式,且拉格朗日插值存在龙格(Runge)现象[5]。因此,本文采用滑动式的拉格朗日算法减少龙格现象的影响。而埃米尔特插值要求不仅在插值节点上函数值相同,在节点上导数值甚至高阶导数值也相同,插值效果较好,但必须给出选取的相应节点的函数值以及导数值,计算量稍大,因为只能保证在一阶导数上连续,所以该方法光滑度不高。三次样条插值则要求一阶,二阶导数值都存在连续,能保证其收敛性和光滑度[6, 7]。具体插值原理参考文献[5-8],本文不再赘述。
1.2 算例分析本文选取多颗颗卫星(编号PRN 8、PRN 15、PRN 20、PRN 24)卫星在2015年11月16~21日的精密钟差。
方案1 将采样率为15 min的钟差使用4种方法插值为5 min钟差;
方案2 将采样率为5 min的钟差使用4种方法插值为30 s钟差。图 1给出了上述4种不同插值方法结果和真值相比较得到的残差,并进行分析。
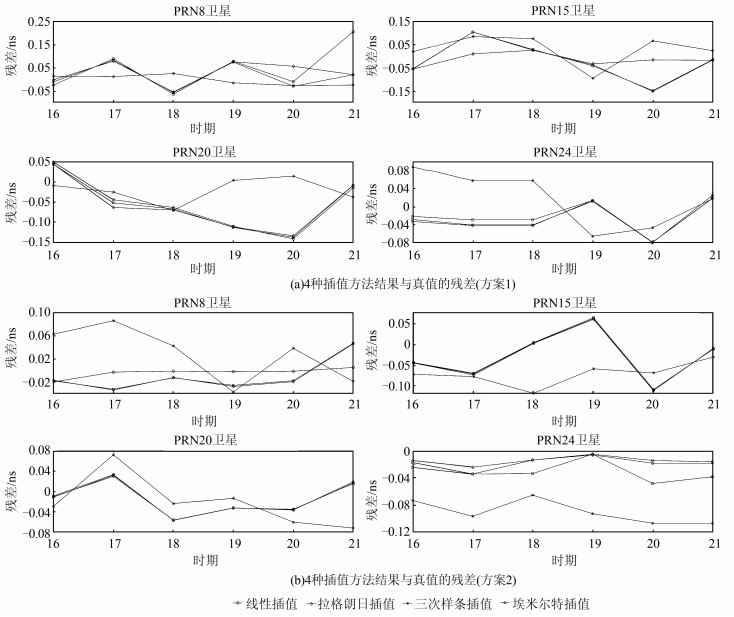 |
| 图 1 4种插值方法结果与真值的残差 Fig.1 Residuals of Four Interpolated Method Results and True Values |
通过对残差的分析,可以得到以下结论:
1) 4种插值方法的精度大致相当,都能达到ns级插值精度,如果不考虑插值方法的稳定程度,可用算法简单的线性插值方法。但当原子钟抖动明显,如15号卫星,简单利用节点值相同的条件构造插值公式不能保证较高精度,三次样条和埃米尔特方法则利用导数值也相同的限制条件构造插值公式,效果较好。
2) 4种插值方法稳定程度上明显不同。线性插值方法由整体基础数据构造插值公式再进行插值。因此稳定程度较高,RMS(root mean spuare)值在0.11~0.34 ns。滑动式拉格朗日插值需要采用不同的节点构造插值公式,节点不同,公式也不同。因此稳定程度不高,RMS值在0.34~0.71 ns。三次样条和埃米尔特插值方法要求不仅节点函数值相同,导数值也相同。因此稳定程度较高,RMS值在0.10~0.21 ns。
3) 对比方案1和方案2,钟差数据采样间隔越短,插值的精度会越高。因此,在实际应用中,应尽可能选择高采样率间隔的钟差产品。
2 利用不同预报模型对精密钟差进行预报本文选取了3种常用的数学模型进行预报GPS导航卫星的精密钟差,分别是线性模型(linear model, LM),二次多项式模型(polynomial model, PM)及灰色系统GM(1, 1)。通过多种方案的算例分析,比较了各个模型在预报钟差的特点。
2.1 预报模型原理简述线性模型通过一次多项式数学模型,拟合出钟差和钟速两个参数,然后进行外推预报钟差。其表达式为:
| $ \Delta {{t}_{i}}={{a}_{0}}+{{a}_{1}}({{t}_{i}}-{{t}_{0}}) $ | (1) |
式中,α0、α1、Δti分别表示原子钟相对于系统时间的相位偏移、频率偏差、ti时刻的钟差。
二次多项式模型与一次多项式模型原理相同,仅在表达式不同,其二次表达式为:
| $ ~\Delta {{t}_{i}}={{a}_{0}}+{{a}_{1}}({{t}_{i}}-{{t}_{0}})+{{a}_{2}}{{({{t}_{i}}-{{t}_{0}})}^{2}} $ | (2) |
式中,α2表示半加速度,其他参数与式(1)意义相同。可见,相比一次多项式模型,二次多项式模型预报原理相同,仅多估计半加速度一个参数。
灰色系统GM(1, 1)是指部分信息(白色)已知,而部分信息未知(黑色)的系统。相比较数据量和计算量都比较大的多项式预报模型,该方法只要原始数列有4个以上数据就可通过生成变换来建立灰色模型。星载原子钟容易受到太空中多因素的影响,变化规律难以完全掌握。因此可以把钟差的变化过程视作是灰色系统,来预测钟差的变化过程[9]。灰色模型GM(1, 1)微分方程为:
| $ \frac{{\rm{d}}x}{{\rm{d}}t}+ax=u $ | (3) |
式中,α,u是待求算的参数。白色信息(灰色区间中的一个可能值)可通过样本或其生成数列求解。设样本的原始数列为[10]:
| $ {{x}^{0}}=\{{{x}^{0}}(1), {{x}^{0}}(2), \cdots , {{x}^{0}}(k), \cdots , {{x}^{0}}(n)\} $ | (4) |
与之对应的时间为(t1, t2, …, tk, …, tn),则通过一次累加可得原始数列生成数列:
| $ {{x}^{1}}=\{{{x}^{1}}(1), {{x}^{1}}(2), \cdots , {{x}^{1}}(k), \cdots , {{x}^{1}}(n)\} $ | (5) |
利用此生成数列即可构建相应的离散预测模型。利用样本的一次累加简历的灰色预测模型为:
| $ {{x}^{1}}(k+1)=[{{x}^{0}}(1)-\frac{u}{a}]{{e}^{-ak}}+\frac{u}{a} $ | (6) |
利用此模型即可获得在时刻t1以后任何时间的参数预测值xt1。利用上述模型计算出的预测值并非原始样本的预测值,而是其一次累加数列的预测值。因此,必须对该预测数列实行一次累加运算,才可以获得原始预测样本的预测值[4]。
2.2 算例分析为验证3种数学模型对卫星钟差预报的特点,以及探讨基础数据,预测时段的不同,本文设计了两种方案进行实例数据分析。
方案1 使用不同时间长度的基础数据去预测相同时间长度的钟差。分别利用2015年11月21日23~24 h的12个历元(间隔5 min),22~24 h的24个历元(间隔5 min),21~24 h的36个历元(间隔5 min),……,12~24 h的144个历元(间隔5 min)的钟差,去预测接下来的11月22日0~1 h内的12个历元(间隔5 min)的钟差。
方案2 使用相同时间长度的基础数据预测不同时间长度的钟差。利用2015年11月21日23~24 h内12个历元(间隔5 min)去预测接下来的11月22日的0~1 h的12个历元(间隔5 min),0~2 h的24个历元(间隔5 min),0~3 h的36个历元(间隔5 min),……,0~12 h的144个历元(间隔5 min)的钟差。
截止2016年4月1日,GPS星座由12颗IIR卫星、8颗IIR-M卫星与12颗IIF卫星组成。卫星搭载的原子钟类型如表 1所示[11]。
| 表 1 GPS卫星及其搭载的原子钟类型信息 Tab.1 Information About GPS Satellites and Its Clocks(2016-04-01) |
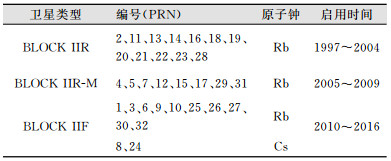 |
为避免不同类型钟的影响,上述两个方案都分别选取了具有代表性的4颗不同类型的卫星,分别是PRN 8(BLOCK IIA,Cs钟)、PRN20(BLOCK IIR,Rb钟)、PRN15(BLOCK IIR-M,Rb钟)、PRN24(BLOCK IIF,Cs钟),其中15、24号卫星钟差呈现曲线递减趋势, 8、20号卫星分别呈现线性递减,递增趋势。预测结果与IGS发布的精密钟差(视作真值)作比较,残差如图 2所示。
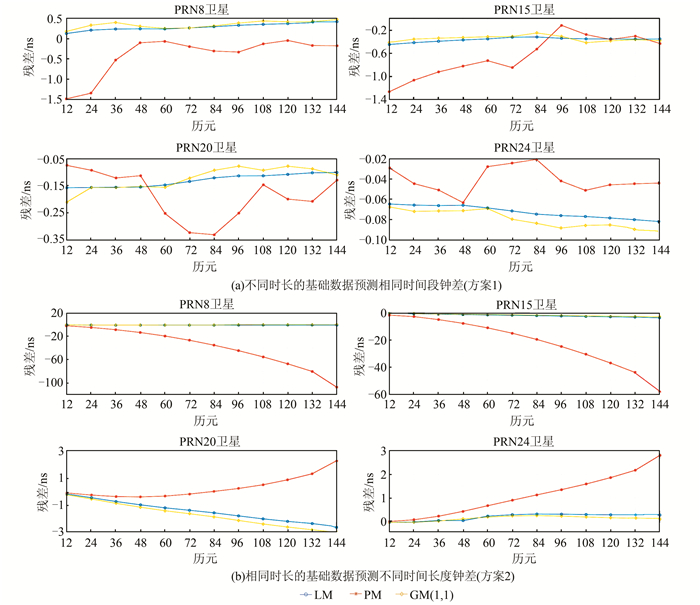 |
| 图 2 不同(相同)时长的基础数据预测相同(不同)时间段钟差 Fig.2 Using Basic Data of Different(Same)Time to Predict Same(Different) Time Period Clock Bias |
通过两个方案的验证可以得到以下结论:
1) LM模型,PM模型,GM(1,1)模型都能够对钟差进行短期预报,精度能够达到ns级别。
2) 方案1表明利用多项式模型拟合2~3个参数,以及灰色系统预报未知信息时,无需过多的基础数据。此外,由于15、24号卫星钟差呈现曲线变化趋势,使用二次多项式模型预报精度更高。8、20号卫星钟差呈现线性趋势,使用线性模型和灰色模型精度更高。当卫星钟差呈现线性变化趋势时,考虑到计算效率,在短期预报中可使用线性模型代替灰色模型。
3) 方案2表明无论哪种模型,预报时间越长,误差积累越多,因此必须考虑预报时长问题。同时,由于卫星钟差变化稳定,在预报长时段钟差时不适合利用二次多项式模型。
3 结束语卫星钟差的插值和预报工作在导航,定位,定轨等方面具有重要意义。
1) 本文首先利用线性插值、拉格朗日插值、三次样条插值、埃米尔特插值等四种不同插值方法将低采样率间隔钟差插值为高采样率钟差,精度都能达到ns级别,但三次样条插值和埃米尔特插值方法在精度和稳定度上比线性插值和拉格朗日插值都要高,且埃米尔特插值方法光滑度不高,建议在实际插值工作中选取三次样条插值方法。
2) 利用多种预报模型进行钟差预报时,精度可达到ns级,且无需大量基础数据。此外,预报时必须考虑原子钟钟差变化趋势特点和预报时长,以选择合适的预报模型。
| [1] |
王宇谱, 吕志平, 陈正生, 等. 一种新的导航卫星钟差预报与内插方法[J]. 大地测量与地球动力学, 2013, 33(4): 112-115. |
| [2] |
崔先强, 焦文海. 灰色系统模型在卫星钟差预报中的应用[J]. 武汉大学学报·信息科学版, 2005, 30(30): 447-449. |
| [3] |
洪樱, 欧吉坤, 彭碧波. GPS卫星精密星历和钟差三种内插方法的比较[J]. 武汉大学学报·信息科学版, 2006, 31(6): 516-518. |
| [4] |
郑作亚, 党亚民, 卢秀山, 等. 附有周期项的预报模型及其在GPS卫星钟差预报中的应用研究[J]. 天文学报, 2010, 51(1): 95-102. |
| [5] |
常远, 林伟华, 徐战亚, 等. 滑动Neville插值算法在GPS精密星历插值中的应用研究[J]. 测绘地理信息, 2017, 42(1): 53-56. |
| [6] |
王俊, 方书山. 精密卫星钟差内插的三种方法及精度分析[J]. 全球定位系统, 2012, 37(4): 49-49. DOI:10.3969/j.issn.1008-9268.2012.04.016 |
| [7] |
李庆扬, 王能超, 易大义. 数值分析[M]. 北京: 清华大学出版社, 2008.
|
| [8] |
鹿德凯, 姜本朋, 曹景庆, 等. 基于拉格朗日多项式的精密星历坐标插值[J]. 北京测绘, 2015(6): 59-60. |
| [9] |
郑作亚, 陈永奇, 卢秀山. 灰色模型修正及其在实时GPS卫星钟差预报中的应用研究[J]. 天文学报, 2017, 42(1): 306-319. |
| [10] |
黎洋, 花向红, 姚周祥, 等. 傅里叶级数修正的动态GM(1, 1)模型在沉降预测中的应用[J]. 测绘地理信息, 2017, 42(1): 30-33. |
| [11] |
王甫红, 夏博洋, 龚学文. 顾及钟差变化率的GPS卫星钟差预报法[J]. 测绘学报, 2016, 45(12): 1387-1395. DOI:10.11947/j.AGCS.2016.20150480 |
 2018, Vol. 43
2018, Vol. 43

