| 基于本质矩阵鲁棒估计的球形全景匹配 |
2. 广州市城市规划勘测设计研究院, 广东 广州, 510060;
3. 武汉大学国家领土主权与海洋权益协同创新中心, 湖北 武汉, 430079
2. Guangzhou Urban Planning Survey and Design Institute, Guangzhou 510060, China;
3. Collaborative Innovation Center for Territorial Sovereignty and Maritime Rights, Wuhan University, Wuhan 430079, China
球形全景相比于普通影像, 具有360°场景全覆盖的优势, 可使控制点的布设更加灵活, 单次恢复更多的场景信息, 提高三维重建的效率, 在虚拟现实、可量测街景[1]方面均具有应用前景。针对球形全景的研究主要集中在如何实现影像拼接缝合[2-5]、影像匹配[6-7]和三维重建[8-9]等方面。其中, 影像匹配是影像拼接缝合和三维重建的关键。
球形全景是球面影像展开为平面的影像, 不仅存在旋转、缩放、仿射等形变, 且几何关系更为复杂, 所以即使采取高级的特征匹配SIFT算法也难以得到较为理想的匹配结果, 通常需要借助其他的约束条件减少误匹配。文献[6]首先在单景鱼眼影像中进行多特征初匹配, 再投影到统一的全景坐标, 引入GPS/IMU数据进行粗剔除, 但GPS/IMU的实际精度评价以及系统误差改正只能通过引入控制点平差完成; 文献[7]利用GPS/IMU数据和全景影像像对间的核线约束, 将原始全景影像转化为核线影像, 再利用SIFT算法进行匹配, 但匹配精度仍有待提高。
本质矩阵是计算机视觉中两视图间对极几何的代数表示[8-9], 摄影测量中通常通过本质矩阵的求解[10]实现普通影像间的相对定向[11-12]和匹配[13]。本文在构建球形全景投影模型的基础上, 推导了球形全景的对极几何关系和仅依赖于本质矩阵的核线方程, 提出了一种基于本质矩阵鲁棒估计的球形全景匹配方法。
1 球形全景的投影模型构建球形全景影像是多台相机通过360°拍摄的影像进行拼接, 形成长方形影像, 并投影到球面形成的。如图 1所示, 设全景球的半径为r, 全景影像ABCD长度方向水平覆盖整个球面, 总长度W=2πr, 宽度方向竖直覆盖半个球面, 总长度H=πr。以点A为原点, 指向B为x轴, 指向D为y轴, 建立像平面坐标系, 同时以球心O为原点, 指向平面全景影像中心o在全景球上的对应点O′为Y轴, 赤道截面为O-XY平面, 建立像空间右手直角坐标系。长方形全景影像ABCD上任意一点p(x, y), 在球形全景影像上存在对应的映射点P(X, Y, Z), 其对应的物方点在像空间坐标系中的坐标为Pc(Xc, Yc, Zc), Pc、P、O满足共线关系。
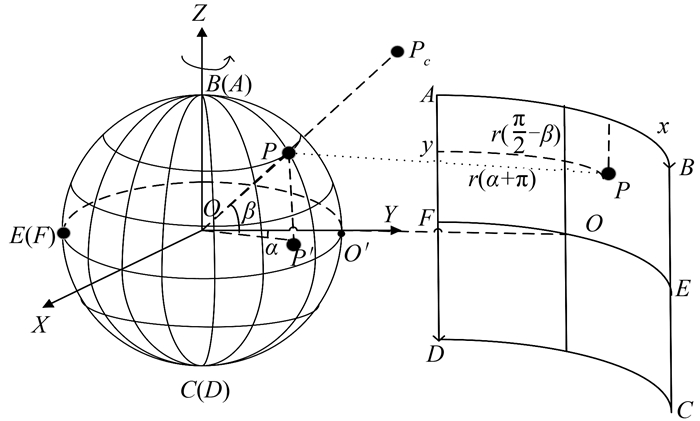 |
| 图 1 球形全景影像与平面全景影像的映射关系 Figure 1 Mapping Relationship Between Spherical Panoramic Imageand Plane Panoramic Image |
如图 1所示, 设点P在O-XY平面上的投影为P′点, 连接OP′与Y轴的夹角为α∈[-π, π], 与OP的夹角为β∈[-π/2, π/2], 顺时针为正, 逆时针为负, 则根据图 1中的映射关系, 点p和点P的坐标值可表示为:
| $ \left\{ \begin{array}{l} x = r(\alpha + \pi )\\ y = r(\frac{\pi }{2}-\beta )\\ r = \frac{W}{{2\pi }} = \frac{H}{\pi } \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} X = r{\rm{cos}}\beta {\rm{cos}}(\frac{\pi }{2}-\alpha )\\ Y = r{\rm{cos}}\beta {\rm{sin}}(\frac{\pi }{2}-\alpha )\\ Z = r{\rm{sin}}\beta \end{array} \right. $ | (2) |
由式(1)、式(2)可推导得像平面坐标点p到球形全景像空间坐标点P的映射关系为:
| $ \left\{ \begin{array}{l} X = r{\rm{cos}}(\frac{{\rm{ \mathsf{ π} }}}{2}-{\rm{ \mathsf{ π} }}\frac{y}{H}){\rm{cos}}(\frac{{3{\rm{ \mathsf{ π} }}}}{2}-2{\rm{ \mathsf{ π} }}\frac{x}{W})\\ Y = r{\rm{cos}}(\frac{{\rm{ \mathsf{ π} }}}{2}-{\rm{ \mathsf{ π} }}\frac{y}{H}){\rm{sin}}(\frac{{3{\rm{ \mathsf{ π} }}}}{2} - 2{\rm{ \mathsf{ π} }}\frac{x}{W})\\ Z = r{\rm{sin}}(\frac{{\rm{ \mathsf{ π} }}}{2} - {\rm{ \mathsf{ π} }}\frac{y}{H}) \end{array} \right. $ | (3) |
如图 2(a)所示, 两相机由其光心C、C′和平面图像表示, 普通相机将物方点M变换到成像平面上, 分别为像点P1、P2, 它们与相机光心C、C′共面, 即为对极面, 对极面与两成像平面相交于对极线l、l′。但图 2(b)所示球形全景投影过程中, 两相机由其光心C、C′和球面图像表示, 将物方点M变换到成像球面上, 分别为像点P1、P2, 成像面不再是平面而是球面, 一般采集存储的数据为平面全景影像, 故需要通过球形全景投影模型将平面全景影像的像点转化为球形全景影像的像点。
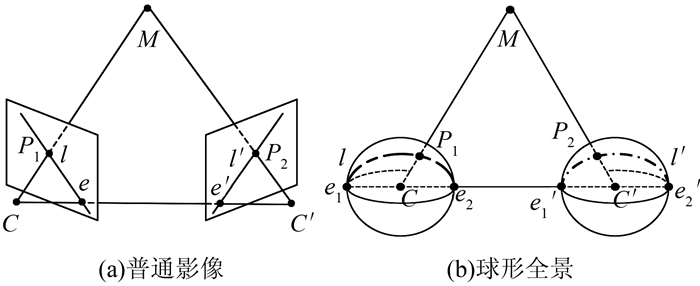 |
| 图 2 普通影像与球形全景的对极几何 Figure 2 Epipolar Geometry of Normal Imageand Spherical Panoramic |
由于球形全景影像投影模型不包含相机内参数, 且半径的大小只影响到影像的缩放比例问题, 为了便于计算, 通常需要将球形全景进行标准化, 即令式(3)中r=1, 则可根据已知的平面全景影像长宽值和像点坐标, 直接将平面全景影像的像点坐标转化为标准球形全景影像下的坐标。
根据本文构建的球形全景投影模型可知, 物方点M和像点P1、光心C共线, 点M、P1、C、C′共面关系(两相交直线唯一确定一个平面), 即为对极面, 该对极面与另一幅球形全景相交成一个圆心为光心C′的大圆, 即为对极线, 由于像点P2与点M、C′共线, 而线MC′在对极面上, 所以像点P2在对极面上, 为此可以推出, 像点P2必然在对极面与其球形全景相交的对极线l′上, 反之像点P1必然在对极面与其球形全景相交的对极线l上, 光心基线CC'与对极线l相交于极点e1、e2, 与对极线l′相交于极点e1′、e2′。
设像点P1、P2的标准球形全景坐标分别为x =(X1, Y1, Z1)T、x′=(X2, Y2, Z2)T, 考虑空间中不通过任何两个相机光心的平面π, 过第一个相机光心C和点P1的射线与平面π相交于物方点M, 该点再投影到第二幅球形全景影像上的一点P2, 这个过程称为通过平面π的转移, 因为点M在对应于点P1的射线上, 它的投影点P2必然在对应于这条射线的图像即对极线l′上, 点P1和P2都是在一张平面上的3D点M的像, 在第一幅球形全景影像上所有这样的点P1的集合和对应点P2的集合是射影等价的, 因为它们都射影等价于共面的点集M, 则根据空间射影几何定理, 存在一个3D单应矩阵K, 把每一个P1映射到P2, 记为:
| $ \mathit{\boldsymbol{x'}} = \mathit{\boldsymbol{Kx}} $ | (4) |
设过像点P2、对极点e1′的直线为l″, 则有:
| $ l'' = {{e'}_1} \times \mathit{\boldsymbol{x'}} $ | (5) |
将式(4)代入式(5)可得:
| $ l'' = {{e'}_1} \times \mathit{\boldsymbol{Kx}} $ | (6) |
又由于P2在直线l″上, 故有x ′Tl″=0, 因而, 有:
| $ {{\mathit{\boldsymbol{x'}}}^{\rm{T}}}{{e'}_1} \times \mathit{\boldsymbol{Kx}} = 0 $ | (7) |
令E =e1′× K, 则有:
| $ {{\mathit{\boldsymbol{x'}}}^{\rm{T}}}\mathit{\boldsymbol{Kx}} = 0 $ | (8) |
从式(8)可以看出, 球形全景的对极几何关系与普通影像是一致的, 可直接利用标准球形全景像点坐标计算出两个球面坐标系统之间的本质矩阵E, 这一结论是显然的, 因为本质矩阵E仅仅表达了两个坐标系之间的旋转和平移关系, 而与坐标系中所表达的点对象是无关的, 无论其在成像平面上还是成像球面上。
3 基于本质矩阵鲁棒估计的球形全景匹配算法 3.1 本质矩阵的求解式(8)表明, 可以通过标准球形全景像点坐标解算两球形全景间的本质矩阵E, 去掉尺度因子后, 本质矩阵E的自由度为8, 故可用8对同名点进行解算。记两平面全景的像点坐标为(xi, yi)T, i=1, 2, 由式(3)可转化为标准球形全景坐标(Xi, Yi, Zi)T, i=1, 2, 此处球形全景半径r取1。球形全景同名点代入式(8)可得方程:
| $ \begin{array}{l} \left[{{\rm{ }}{X_1}{X_2}\;{Y_1}{X_2}\;{Z_1}{X_2}\;{X_1}{Y_2}\;{Y_1}{Y_2}\;{Z_1}{Y_2}\;{X_1}{Z_2}\;{Y_1}{Z_2}\;{Z_1}{Z_2}} \right]\\ \times \mathit{\boldsymbol{\tilde E}} = 0 \end{array} $ | (9) |
式中,
解算出本质矩阵E后, 即可确定两视图的对极几何关系。对于普通影像第一幅视图中的任意一点q =(x, y)T, 假定任意一个过点q的直线ax+by+c=0可以参数化表示为(a, b, c)T, 那么该点在第二幅视图中对极线的参数化表示由l = Ex计算得到。
对于全景视图, 由于其成像面为球面, 故物方点M和其在图像球面的像点P1、P2与相机光心C、C′所在的平面与之相交不再是直线, 而是过球心的一个大圆。对于一幅球形全景视图中的任意一个像点Q =(X, Y, Z)T, 假定任意一个过点Q的平面aX+bY+Cz+d=0参数化表示为(a, b, c, d)T, 则任意一个过原点的平面可参数化表示为(a, b, c)T。同理, l = Ex为过另一幅球形全景视图光心C′的一个平面, 又由像点P1的同名点P2满足x′T Ex = x ′Tl = 0, 可知该平面为一幅球形全景视图中的像点P1在另一幅球形全景视图中对应的对极面, 则球形全景的对极线可表示如下:
| $ \begin{array}{l} {右极线}:\left\{ \begin{array}{l} {\left[{A\prime \;B\prime \;C\prime } \right]^{\rm{T}}} = \mathit{\boldsymbol{E}}x\\ A\prime {X_2} + B\prime {Y_2} + C\prime {Z_2} = 0\\ {\rm{ }}X_2^2 + Y_2^2 + Z_2^2 = 1 \end{array} \right.{\rm{ }}\\ {左极线}:\left\{ \begin{array}{l} {\left[{A\;B\;C} \right]^{\rm{T}}} = \mathit{\boldsymbol{E}}{^{\rm{T}}}x\prime \\ A{X_1} + B{Y_1} + C{Z_1} = 0\\ {\rm{ }}X_1^2 + Y_1^2 + Z_1^2 = 1 \end{array} \right. \end{array} $ | (10) |
针对球形全景本质矩阵解算的结果, 本文提出基于改进的Sampson距离[13]算子进行精度评价。
假设全景像点P1、P2构成点X=(x, x′), 最小化几何误差
| $ F\left( {\mathit{\boldsymbol{\hat X}}} \right) = F\left( \mathit{\boldsymbol{X}} \right) + \frac{{\partial F}}{{\partial \mathit{\boldsymbol{X}}}}\left( {\mathit{\boldsymbol{\hat X}}-\mathit{\boldsymbol{X}}} \right) = 0 $ | (11) |
其中, 称
| $ \begin{array}{l} {d_i} = \\ \frac{{{{({{\mathit{\boldsymbol{x'}}}_i}^{\rm{T}}\mathit{\boldsymbol{Ex}}{_i})}^2}}}{{\left( {\mathit{\boldsymbol{Ex}}{_i}} \right)_1^2 + \left( {\mathit{\boldsymbol{Ex}}{_i}} \right)_2^2 + \left( {\mathit{\boldsymbol{Ex}}{_i}} \right)_3^2 + {{({\mathit{\boldsymbol{E}}^{\rm{T}}}{{\mathit{\boldsymbol{x'}}}_i})}}_1^2 + ({\mathit{\boldsymbol{E}}^{\rm{T}}}{{\mathit{\boldsymbol{x'}}}_i})_2^2 + ({\mathit{\boldsymbol{E}}^{\rm{T}}}\mathit{\boldsymbol{x'}})_3^2}}, i = 1, 2, \ldots, N \end{array} $ | (12) |
式中, i表示当前对应点的序号; N表示对应点的对数。
上述改进的Sampson距离算子在原理上和点到极线的距离最小类似, 可获得参与本质矩阵解算的所有对应点的Sampson距离, 并求出误差均值, 称为内符合精度, 也可针对其他对应点解求Sampson距离, 对模型精度进行评价, 称为外符合精度。在本文提出的基于本质矩阵鲁棒估计的匹配算法中, 就是通过样本数据求解模型, 其他数据进行外符合精度评价的方式, 对模型精度进行评价, 以获得最佳的模型和本质矩阵。
3.4 基于本质矩阵鲁棒估计的匹配算法在实际应用中, 通常通过SIFT算法进行特征提取与匹配获取球形全景同名点对, 其对数往往大于8, 且存在误匹配, 需对误匹配进行剔除, 故本文采用RANSAC算法, 通过对存在误差的同名点数据进行多次随机采样, 可在满足一定精度的条件下确定最多的内点集合, 从而求得最佳的本质矩阵, 实现球形全景本质矩阵的鲁棒估计以及误匹配的剔除, 其算法流程如下。
1) 在一对球形全景的匹配点数据集中取样, 采用8点算法解算初始本质矩阵E。
2) 利用改进的Sampson距离算子计算非取样数据的Sampson距离, 并设定距离阈值, 划分数据为内点和外点。
3) 记录当前初始估计的本质矩阵和内点的数目并进行比较, 保存内点数目最多的本质矩阵。
4) 将以上步骤循环n次, 构造出n个基本子集, 概率p表示至少有一个数据基本子集包含的数据全部是内点数据的概率, 通常该概率大于95%, 这样, 基本子集数n与概率p之间满足如下关系:p=1-(1-εs)n, 其中s表示基本子集中数据点的数目, 本文取s=8, ε表示内点占数据集的比例, 则可求得循环的次数n=lg(1-p)/lg(1-ε8)。
5) 得到内点最多的本质矩阵初始估计E和相应内点, 即对误匹配进行剔除。
6) 将所有内点重新利用8点算法得到本质矩阵。
4 实验结果与分析采用Ladybug5全景相机移动车载测量系统作为实验平台, 采集了天津某区域的街景数据, 其分辨率为2 048像素×1 024像素, 用其中三组任意相邻的两张全景影像作为实验对象(由于车体属于全景相机移动车载测量系统的载体, 故去除车体不参与匹配), 利用SIFT算法提取两全景影像的特征点并进行初匹配后(其特征点数和初匹配点数见表 1), 设置本质矩阵估计模型的Sampson距离阈值为0.000 1, 小于阈值的为内点, 采用RANSAC算法对两全景影像进行本质矩阵鲁棒估计和粗差剔除(剔除的误匹配点数见表 1), 得到的匹配结果见图 3。
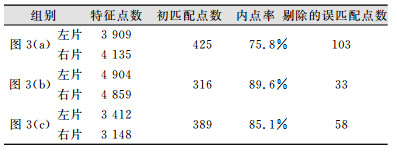
| 表 1 球形全景特征提取和匹配结果 Table 1 Features Extraction and Matching Result of Spherical Panoramic |
 |
 |
| 图 3 球形全景初匹配与粗差剔除(去除车体) Figure 3 First Matching and Gross Error Removing of Spherical Panoramic (Car Removed) |
由表 1可以看出, 虽然通过SIFT算法提取的特征很多, 但匹配下来的同名点却相对较少, 仅占总数量的15%, 这与球形全景平面影像存在旋转、缩放、仿射甚至更加复杂的形变有关。由内点率可知, 基于本质矩阵鲁棒估计的球形全景匹配保留了大部分的初匹配结果。从图 3对比结果可以看出, 一些明显的误匹配点(图中斜率较大的连线)在基于本质矩阵鲁棒估计的匹配算法中被剔除。为了进一步分析, 选取了第1组球形全景数据, 抽取易于目视识别的Sampson距离大于0.01的误匹配点, 如图 4所示, Sampson距离评价的是匹配点加上对极线约束后的符合精度, 图 4(a)中编号为3、7、8、9的匹配点具有较大的Sampson距离值, 可以看出相应的图 4(b)中该4对匹配点的匹配误差较大, 即加上对极几何约束后, 可利用Sampson距离精度评价算子剔除误匹配。实验表明, 将基于本质矩阵鲁棒估计的匹配方法用于球形全景影像匹配可以减少误匹配点, 提高匹配精度。
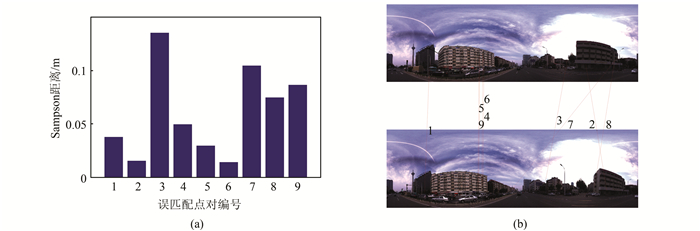 |
| 图 4 误匹配点与Sampson距离 Figure 4 Miss Matching Point and Sampson Distance |
同时, 为验证球形全景基本矩阵估计的正确性, 选取了第1组球形全景数据, 根据其估计的本质矩阵, 从一幅视图任意选取一点, 计算出另一幅视图的对极线(图 5)。
 |
| 图 5 球形全景对极线约束(去除车体) Figure 5 Epipolar Geometry Constraint of Spherical Panoramic (Car Removed) |
图 5中, 十字丝表示任意选取的点, 曲线表示其对应的在另一视图中的对极线。从图 5中可以看出, 对极线过任意选取的点的同名点, 从而验证了通过RANSAC算法对球形全景本质矩阵进行鲁棒估计和匹配是可行的。
5 结束语球形全景以其场景全覆盖的优势, 正在虚拟现实、可量测街景方面得到越来越多的应用, 球形全景匹配是实现这些应用的前提。本文通过构建球形全景投影模型和推导球形全景对极几何关系, 提出了一种基于基本矩阵鲁棒估计的球形全景匹配算法。实验表明, 本文方法能够提高球形全景匹配的精度, 且通过对极线的求解结果说明, 对本质矩阵的鲁棒估计是正确可行的。
进一步研究工作将从基于球形全景的三维重建着手, 实现球形全景的相对定向、绝对定向和前方交会, 从而更好地实现球形全景的量测和建模功能。
| [1] |
柯晓龙, 李建松, 刘金榜, 等. 基于可量测街景的广告牌管理系统设计与实现[J]. 测绘地理信息, 2015, 40(2): 71-73. |
| [2] |
李晓辉, 周荫清, 王祖林. 基于曲面拼接的球面全景生成算法[J]. 北京航空航天大学学报, 2007, 33(6): 668-671. |
| [3] |
龚琪慧, 吴健平, 王洁华, 等. 基于全景图的3维实景制作及其与GIS集成研究[J]. 测绘与空间地理信息, 2012, 37(6): 33-37. |
| [4] |
Tong Guofeng, Pang Xiaolei, Ye Ning, et al. A Precise Spherical Camera Model Based on Multi-camera System[J]. Journal of Computational Information Systems, 2013, 9(3): 897-905. |
| [5] |
Brown M, Lowe D G. Automatic Panoramic Image Stitching Using Invariant Features[J]. International Journal of Compute Revision, 2007, 74(1): 59-73. DOI:10.1007/s11263-006-0002-3 |
| [6] |
季顺平, 史云. 车载全景相机的影像匹配和光束法平差[J]. 测绘学报, 2013, 42(1): 94-100. |
| [7] |
曾凡洋, 钟若飞, 宋杨, 等. 车载全景影像核线匹配和空间前方交会[J]. 遥感学报, 2014, 18(6): 1 230-1 236. |
| [8] |
刘帅, 陈军, 孙敏, 等. 一种球形立体全景的三维量测算法与实验[J]. 地球信息科学学报, 2014, 16(1): 15-22. |
| [9] |
Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[M]. 2nd eds. Cambridge: Cambridge University Press, 2004.
|
| [10] |
吴春富, 唐庆顺, 谢煌生, 等. 一种新型的本质矩阵解析分解算法[J]. 山东大学学报(理学版), 2014, 49(3): 31-36. |
| [11] |
Nistér D. An Efficient Solution to the Five-point Relative Pose Problem[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 2004, 26(6): 756-770. DOI:10.1109/TPAMI.2004.17 |
| [12] |
李云雷, 蒋灵搏. 近景摄影测量中基于本质矩阵分解的相对定向算法[J]. 山东理工大学学报(自然科学版), 2015, 29(5): 53-56. |
| [13] |
单欣, 王耀明, 董建萍. 基于RANSAC算法的基本矩阵估计的匹配方法[J]. 上海电机学院学报, 2006, 4(1): 66-69. |
 2018, Vol. 43
2018, Vol. 43

