| 利用傅里叶级数有限项的路基沉降预测模型 |
2. 兰州石化职业技术学院土木工程系,甘肃 兰州,730060
2. Department of Civil Engineering, Lanzhou Petrochemical College of Vocational Technology, Lanzhou 730060, China
高速公路、高速铁路在施工期和工后运期都会出现路基沉降现象。有效控制路基沉降对公路安全和铁路安全有着重要意义,而有效控制路基沉降一个重要的方法是做好路基沉降变形预测。目前的预测方法有时间序列分析法[1, 2]、曲线拟合法[2, 3]、灰色理论[4, 5]和神经网络方法[6]等,这些方法均取得了不错的预测效果。本文在前人研究成果的基础上提出一种基于傅里叶级数的预测方法,该方法具有很强的数据处理能力和外推能力,只需少量的级数项就能够达到理想的拟合预测效果,对于其中的级数项系数采用遗传算法来估算。算例分析表明,从傅里叶级数提取的预测模型的预测效果较其他一些预测方法好,为路基沉降预测提供了一种新方法。
1 傅里叶级数对于任意一个在闭区间[-l, l]上连续或至多仅有有限个第一类间断点与极值点的函数f(x)都能够表示成如下的形式[7]:
| $ f\left( x \right) = \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {} ({a_n}{\rm{cos}}\frac{{n{\rm{\pi }} x}}{l} + {b_n}{\rm{sin}}\frac{{n{\rm{\pi }} x}}{l}) $ | (1) |
式中,
| $ \begin{array}{l} {a_n} = \frac{1}{l}\int_{-l}^l {f(x){\rm{cos}}\frac{{n{\rm{\pi }} x}}{l}{\rm{d}}x} \\ {b_n} = \frac{1}{l}\int_{-l}^l {f(x){\rm{sin}}\frac{{n{\rm{\pi }} x}}{l}{\rm{d}}x} \\ \;\;\;\;\;\;(n = 0, 1, 2, \cdots ) \end{array} $ |
式(1) 右端的级数称为f(x)的傅里叶级数。对于定义在[0, l]上的函数f(x),可以通过任意延拓至区间[-l, 0),使函数f(x)依然有式(1) 的级数表达。傅里叶级数的前n项和
由于路基沉降是一个渐变的过程,沉降量是时间的函数,在有限的时间段内(或许是一个较长的时间段)研究沉降才具有工程意义,所以可以用傅里叶级数来表达沉降量函数f(t)(t为观测期数)。在实际应用中,只需用傅里叶级数的有限项和Sn0(t)项就可以达到理想的近似效果。由于沉降函数f(t)未知,因此可用观测数据来估算傅里叶系数和参数
文献[9]给出了武汉某高铁路基的一组沉降原始观测数据,如表 1所示。
| 表 1 沉降原始观测数据 Table 1 Settlement Original Observation Data |
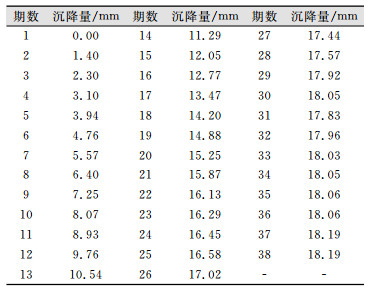 |
以表 1中38期的观测数据建模,并做观测期数-沉降量散点图,如图 1所示。
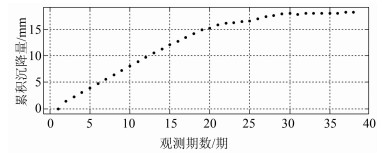 |
| 图 1 原始数据散点图 Figure 1 Scatter Diagram of Original Data |
2.2 模型参数估计
采用遗传算法估算模型
| $ {S_n}\left( t \right) = \frac{{{a_0}}}{2} + \sum\limits_{k = 1}^n {({a_k}{\rm{cos}}\frac{{k{\rm{\pi }}x}}{l} + {b_k}{\rm{sin}}\frac{{k{\rm{\pi }}x}}{l})} $ |
的参数。从模型决定系数(拟合优度)、残差分析来看,当n=1时,拟合效果不理想;当n>2时,拟合效果与n=2时相比没有明显改善,而且加大了运算量,所以选择n=2时的模型为本算例的拟合预测模型。下面给出n=2时参数估计的遗传算法及估算结果。适应度函数为:
| $ {\rm{Fitness}} = \frac{1}{{38}}\sum\limits_{i = 1}^{38} {{{({y_i}-{S_2}\left( i \right))}^2}} $ | (2) |
式中,yi为表 1中第i期的观测沉降量;S2(i)为模型的计算沉降量。利用最小二乘法估算出模型的参数范围为:
在MATLAB工作窗口利用gatool命令打开遗传算法的GUI[10, 11], 在Fitness Function窗口输入@Fitness,在Number of Variables窗口输入待估参数个数6,在边界约束Lower输入[9,-14,3,-1.851,2,-0.072], 在Upper输入[14,-9.5,7,-0.022,6.8,0.164], 种群规模为50,迭代次数为2 000,其他参数选用缺省值,然后单击Start按钮执行遗传算法。适应度函数的变化过程如图 2所示,最优适应度函数值为0.994 502。
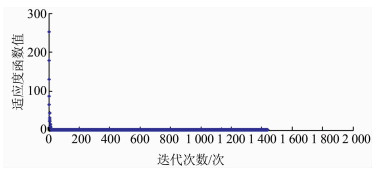 |
| 图 2 适应度函数变化曲线 Figure 2 Change Curve of Fitness Function |
迭代1 440次后终止,输出的参数值为:
| $ \begin{array}{l} {S_2}\left( t \right) = 11.017{\rm{ }}07-10.798{\rm{ }}11{\rm{cos}}\left( {0.051{\rm{ }}71t} \right) + \\ \;\;\;\;\;\;6.212{\rm{ }}75{\rm{sin}}\left( {0.051{\rm{ }}71t} \right)-\\ \;\;\;\;\;0.651{\rm{ }}53{\rm{cos}}\left( {2 \times 0.051{\rm{ }}71t} \right) + \\ \;\;\;\;\;\;\;4.481{\rm{ }}35{\rm{sin}}\left( {2 \times 0.051{\rm{ }}71t} \right) \end{array} $ | (3) |
模型的显著性检验如下:决定系数R2=0.999 2,调整的决定系数R2=0.999 1,残差平方和SSE=0.991 4 mm,均方误差MSE=0.026 1 mm,表明模型拟合效果显著(拟合效果如图 3所示),可靠性强,可用于后期的沉降预测。
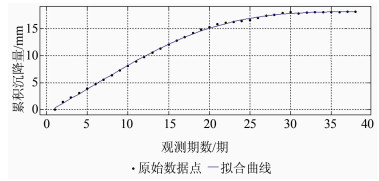 |
| 图 3 模型拟合效果图 Figure 3 Fitting Effect of Model |
2.3 预测分析
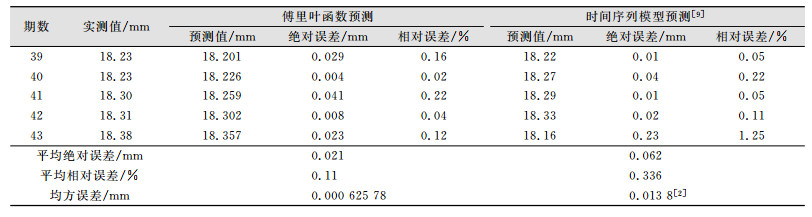
用傅里叶函数预测模型式(3) 预测后5期的沉降量,结果如表 2所示,并将预测值与实际测量值进行比较,得出均方误差MSE=0.000 63 mm。由于对建模数据未进行消噪处理,故选文献[9]消噪前的时间序列预测模型为:
| 表 2 预测结果分析及比较 Table 2 Comparison and Analysis of Prediction Results |
 |
| $ \begin{array}{l} {Y_t} = 1.496\;3{Y_{t-1}}-0.288\;5{Y_{t-2}} + \\ 0.088\;1{Y_{t - 3}} - 0.295\;9{Y_{t - 4}} + {\xi _t} \end{array} $ | (4) |
该模型对后5期的沉降预测结果如表 2所示,求得均方误差为MSE=0.013 8 mm。
从预测精度分析来看,基于傅里叶级数的预测模型的预测精度较时间序列模型有较大改善。随着预测期数的增加,时间序列模型的预测精度有明显降低的趋势,而傅里叶级数预测模型的预测精度的稳定性较好,可以更好地用于高铁沉降预警。
3 结束语傅里叶级数能够表达连续函数(仅有有限个第一类间断点与极值点的函数也可以),从首项开始的部分和随着项数的增加能够不断逼近被表达函数,所以特别当函数解析式未知时,从理论保证了能够用该级数的部分和拟合函数曲线。路基沉降是时间的函数,其函数解析式未知,因此,可用傅里叶级数部分和来逼近它。另外,从傅里叶级数里提取拟合预测模型的关键在于模型参数的估计和残差分析,本文采用遗传算法估算模型参数。实证分析表明,基于遗传算法的傅里叶级数提取模型具有较高的精确度,有一定的工程意义和借鉴意义。
| [1] | 王刘准, 邱卫宁, 花向红, 等. 小波时间序列分析在高铁沉降变形中的应用[J]. 测绘地理信息, 2013, 38(4): 45–47 |
| [2] | 何超, 黄声享, 陈启文, 等. 基于数据残差的AR模型在高铁路基沉降预测中的应用[J]. 测绘工程, 2011, 20(5): 53–56 |
| [3] | 甄京山. 曲线拟合法在软土路基沉降预测中的应用[J]. 公路交通科技, 2012, (11): 195–197 |
| [4] | 郑建国, 王婷, 张继文. 黄土路基沉降量预测方法的研究[J]. 岩土力学, 2010, 31(1): 321–326 |
| [5] | 陈威, 唐德燕, 张届. 利用三点法-灰色组合模型预测铁路路基沉降[J]. 测绘科学, 2015, 40(7): 37–40 |
| [6] | 刘军勇, 薛辉, 吴德军. 改进灰色模型对路基沉降预测的应用研究[J]. 四川地质学报, 2005, 25(3): 164–168 |
| [7] | 徐世强, 梁武星, 屈战辉. BP神经网络在预测路基沉降中的应用[J]. 西安工业大学学报, 2006, 26(5): 452–456 |
| [8] | 伍胜健. 数学分析(第二册)[M]. 北京: 北京大学出版社, 2015 |
| [9] | 刘闯, 花向红, 赵杰, 等. 基于小波去噪的高铁沉降预测模型研究[J]. 测绘地理信息, 2015, 40(1): 37–40 |
| [10] | 许国根, 贾瑛. 模式识别与智能计算的MATLAB实现[M]. 北京: 北京航空航天大学出版社, 2012 |
| [11] |
龚纯, 王正林. 精通MATLAB最优化计算[M]. 2版. 北京: 电子工业出版社, 2012 |
 2017, Vol. 42
2017, Vol. 42

