| WiFi定位邻近个数对位置估计的影响 |
2. 武汉大学测绘学院, 湖北 武汉, 430079;
3. 武汉大学灾害监测与防治研究中心,湖北 武汉,430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Hazard Monitoring & Prevention Research Center, Wuhan University, Wuhan 430079, China
大数据处理和数据挖掘的发展加快了人们对信息的需求,室内位置的可靠估计具有广阔的应用前景。由于GPS受到非通视的影响[1-4],基于RSSI指纹的WiFi定位技术成为目前室内定位技术的一个不可替代的技术[5-8]。考虑到WiFi定位技术需要的硬件基础设施为普遍存在的WiFi信号发射器,即AP热点。WiFi技术的应用可以尽可能地缩减位置估计带来的成本。20世纪90年代以来,国内外学者对WiFi定位技术进行了研究。然而,对基于RSSI指纹匹配[9-11]的WiFi定位技术的指纹邻近点的个数选取依旧存在着混乱的现象。出现这一现象的主要原因是由于室内环境的复杂性和时间变动性,AP的无线电信号的衰减难以模型化。指纹匹配个数设置的任意性对室内定位的精度和可靠度具有明显的影响。本文研究了指纹匹配点的个数对位置估计和邻近点选取可靠度的影响。通过位置估计的精度和可靠度以及邻近点包围检验算法给出了单个房间内的指纹匹配的最佳邻近点个数。
1 基于RSSI指纹的WiFi定位算法RSSI为无线电信号接收器接收到的WiFi的信号强度指标。基于RSSI指纹的WiFi定位算法主要分为两部分:线下的数据采集阶段和线上的位置估计阶段。
1.1 线下数据采集阶段线下阶段主要完成构成RSSI信号空间地图的数据采集,即采集已知物理位置的参考点上的RSSI信息,然后建立数据库。WiFi定位中通常将已知位置的参考点以及其关联的RSSI数据信息称为指纹点。所有的指纹点构成指纹匹配的数据库,其基本数据单元存储一个指纹点的信息,格式为 (x, y, ssid, rssi)。(x, y) 表示指纹点的物理位置坐标,ssid和rssi表示指纹点观测到的AP的识别号序列和对应的RSSI特征值序列。
1.2 线上的位置估计阶段线上阶段利用位置估计点的RSSI信息与数据库中的数据进行指纹匹配,进行位置估计。一般采用KNN邻近点搜索算法实现位置估计的邻近指纹点搜索,即指纹点匹配。其基本的数学原理如下:
| $ {{d}_{\text{signal}}}=\text{sqrt}(\sum\limits_{i=1}^{N}{{{(\text{rssi}_{P}^{i}-\text{rssi}_{FP}^{i})}^{2}}}) $ | (1) |
式中, i表示AP的编号; N表示参与计算的AP的个数;P表示位置估计点; FP表示指纹点;dsignal表示位置估计点和指纹点的信号空间的欧氏距离;rssiPi和rssiFPi分别表示位置估计点和指纹点的指定AP的RSSI信号特征值;sqrt () 表示开均方根。
利用式 (2) 计算位置估计点与所有指纹点的信号空间的欧氏距离,找出距离最小的K个指纹点,即需要的指纹匹配点。
目前存在大量的基于RSSI指纹的WiFi位置估计算法,本文采用通用的稳定的信号空间距离反比例加权算法进行位置估计。假定利用指纹匹配算法找到了K个信号空间最邻近的指纹点,位置估计的一般算法如下:
| $ ({{x}_{p}}, {{y}_{P}})=\sum\limits_{i=1}^{K}{{{w}_{i}}}(x_{FP}^{i}, y_{FP}^{i}) $ | (2) |
式中, (xP, yP) 表示位置估计点的坐标;(xFPi, yFPi) 表示第i个指纹点的坐标;K为邻近指纹点的个数;wi表示第i个指纹点的距离归一化后的权重:
| $ {{w}_{i}}=\left( \frac{1}{d_{P}^{F{{P}_{i}}}} \right)/\left( \sum\limits_{j=1}^{K}{\frac{1}{d_{P}^{F{{P}_{j}}}}} \right) $ | (3) |
式中,dPFPi表示位置估计点与第i个邻近指纹点的距离;dPFPj表示位置估计点与第j个邻近指纹点的距离;K表示邻近指纹点的个数。
2 WiFi定位邻近指纹匹配点最佳个数的确定指标单个位置估计点的误差计算公式如下:
| $ \Delta d=\text{sqrt}({{({{x}_{p}}-{{x}_{\text{real}}})}^{2}}+{{({{y}_{p}}-{{y}_{\text{real}}})}^{2}}) $ | (4) |
式中,Δd表示位置估计点的位置估计误差;(xp, yp) 表示位置估计点的估计坐标;(xreal, yreal) 表示位置估计点的实际物理位置坐标。
由式 (4) 可以看出,基于RSSI指纹的WiFi定位算法的位置估计结果与指纹匹配点的精度和个数紧密相关。为了研究指纹匹配点个数对位置估计的影响,本文提出了3个评价指纹点个数的确定指标,即位置估计的精度、可靠度以及邻近点搜索的可靠度。
2.1 位置估计精度指标定义精度为所有参与计算的位置估计点的误差的均值:
| $ \delta =\frac{1}{N}\sum\limits_{i=1}^{N}{\Delta {{d}_{i}}} $ | (5) |
式中,δ表示位置估计的精度;N表示所有参与检验的位置估计点的个数;Δdi为第i个位置估计点的误差。
2.2 位置估计可靠度指标定义可靠度为位置估计误差小于某一限差的百分比:
| $ {{\beta }_{\alpha }}=\frac{{{n}_{\alpha }}}{N} $ | (6) |
式中,N表示所有参与检验的位置估计点的个数;nα表示位置估计点中估计误差小于阈值α的位置估计点的个数;βα表示可靠度,为百分比形式。
2.3 邻近点搜索可靠度指标位置估计的邻近点搜索的可靠度为位置估计点的实际位置位于邻近点的最大包围盒内部的个数的百分比。假定xmax、xmin、ymax、ymin表示位置估计点的K个指纹匹配点的物理位置坐标的x和y的最大、最小值,则指纹匹配的邻近点构成的最大包围盒为由4个点 (xmin, ymin)、(xmin, ymax)、(xmax, ymax) 和 (xmax, ymin) 构成的矩形。位置估计点的实际位置位于邻近点的最大包围盒的内部应满足下式:
| $ {{x}_{\min }}\le {{x}_{real}}\le {{x}_{\max }}\And {{y}_{\min }}\le {{y}_{real}}\le {{y}_{\max }} $ | (7) |
式中, & 表示同时满足左右两个不等式;(xreal, yreal) 表示位置估计点的实际物理位置坐标。邻近点搜索的可靠度计算如下:
| $ \beta =\frac{n}{N} $ | (8) |
式中,β表示邻近点搜索的可靠度;n表示位置估计点的实际位置位于邻近点的最大包围盒内部的个数;N表示所有参与位置检验的位置估计点的个数。
3 实验及结果分析为了检验指纹匹配点的个数设置对位置估计的影响,利用本文提出的3个评价指纹点个数的确定指标,通过实验实测数据进行了研究和分析。实验采用6个无线路由器作为信号发射器,即AP,信号接收器采用小米手机。线下阶段的数据采集位于一个中型大小的办公环境,室内面积大小约为7 m×7 m。分别采集了28个指纹点和64个位置估计点,其具体的分布如图 1所示。
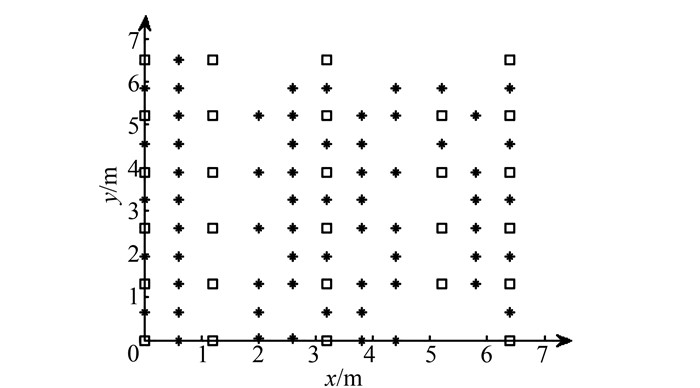 |
| 图 1 指纹点和位置估计点的分布示意图 Figure 1 Schematic Diagram of Fingerprint and Locating Points |
图 1中,“*”表示位置估计点的物理位置,“□”表示指纹点的物理位置。指纹点采取尽量均匀分布的策略进行选取,位置估计点则分布在整个房间的任意位置,减少位置估计点的选取带来的结果的特殊性。由于RSSI特征值构成的信号空间与物理欧氏空间没有严格的对应关系,通过KNN搜索算法利用信号空间的欧氏距离搜索物理空间的邻近点时,获取的指纹匹配点并不是真实物理空间中的邻近点。甚至部分点的搜索位于邻近指纹点的最大包围和外部。
图 2给出了信号空间距离分布图。不同的颜色表示物理位置点对应的信号空间的点距离信号空间原点的距离,颜色相同的物理位置在信号空间距离信号空间原点的距离一样。
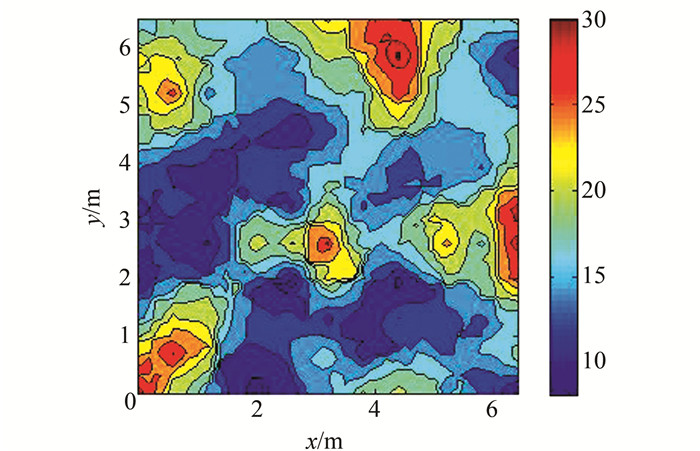 |
| 图 2 信号空间距离分布图 Figure 2 Schematic Diagram of Signal Space Distance |
由图 2可以看出,虽然物理位置相差较大的两个点在信号空间中可能离信号空间的原点的距离是一样的,但是利用信号空间的欧氏距离匹配算法并不能完全正确地找到距离位置估计点物理位置最近的多个点。
图 3给出了搜索的指纹匹配点示意图,图中的“*”表示位置估计点的实际物理位置,“□”表示指纹匹配算法搜索到的匹配指纹点的实际物理位置。
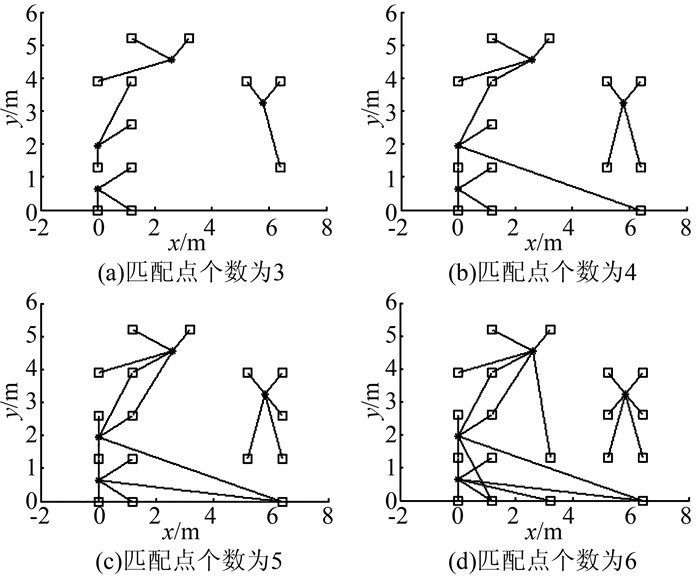 |
| 图 3 搜索的指纹匹配点示意图 Figure 3 Schematic Diagram of Fingerprint Matching Points |
由图 3可以看出,指纹匹配算法搜索到的匹配指纹点具有很大的随机性。图 3(a)、3(b)、3(c)、3(d) 分别表示邻近指纹点的个数参数分别设置为3~6时搜索到的邻近指纹点示意图。由于篇幅限制,这里仅仅给出部分位置估计点的指纹匹配结果。
图 4给出了位置估计实验结果的可靠度统计信息,横坐标为指纹匹配的邻近点个数,“*”表示位置估计误差小于1 m的可靠度,“□”表示位置估计误差小于2 m的可靠度,“☆”表示位置估计误差小于3 m的可靠度,“▽”表示包围盒检验的可靠度。
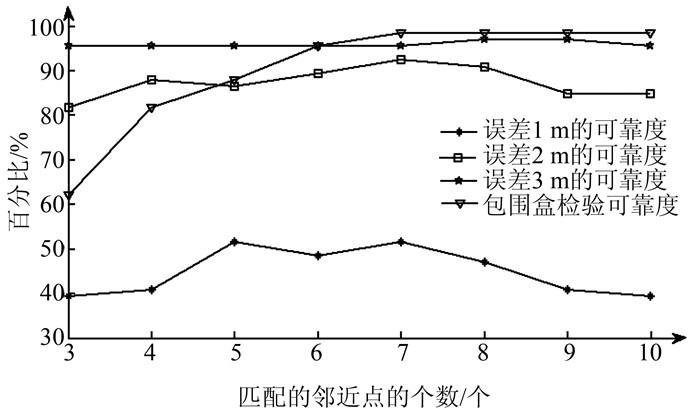 |
| 图 4 统计结果图 Figure 4 Schematic Diagram of Statistical Results |
由图 4可以看出,包围盒检验的可靠度开始随着邻近点的个数增加而线性增加,邻近点个数大于6后趋于平稳。
表 1给出了位置估计结果的精度和可靠度的详细信息,以及邻近点包围盒检验的结果。β1、β2、β3分别表示所有参与计算的估计位置点中的估计位置与实际位置的距离小于1 m、2 m和3 m的位置估计点个数的百分比;β表示位置估计点实际位置位于邻近点的最大包围盒内部的点的个数的百分比;δ表示位置估计的精度;K表示指纹匹配算法的邻近点个数,分别设置为3~10。
| 表 1 结果检验表 Table 1 Result Inspection Table |
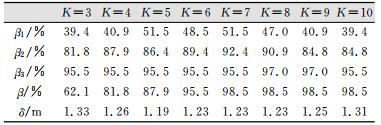 |
由表 1可以看出,K设置为3~10的位置估计的精度和可靠性差异不大;K=3时,精度和可靠度最差;K=5时,精度最高,β1最大,即误差小于1 m的可靠度最高;K=7时,β1、β2最大,即误差小于1 m和2 m的可靠度最高;K=8和9时,β3最大,即误差小于3 m的可靠度最高;K=6~9时,δ相差很小,其位置估计的精度相当;而K=6~10时,β均为最大值,说明邻近点包围盒检验的可靠度最好。
根据表 1的结果,为了兼顾位置估计的精度和可靠度以及邻近点匹配算法的可靠度,合理的邻近点个数参数设置应该为5~8个。
4 结束语本文对基于RSSI指纹匹配的WiFi定位技术进行了研究,重点比较分析了不同指纹匹配算法的指纹点个数对位置估计的影响。利用试验数据,通过分别设置指纹匹配点的个数为K=3~10,利用WiFi定位技术估计了任意分布的多个位置估计点的位置。试验结果表明,当K=5时,位置估计的精度最高,误差小于1 m的可靠度最好;K=6~8时,位置估计的精度次优,并且邻近点的包围盒检验最优,即邻近点匹配最优;K=7时,误差小于2 m的可靠度最好。因此建议设置指纹匹配算法的指纹点匹配个数为5~8个。
| [1] | Yao Y, Chen P, Zhang S, et al. A New Ionospheric Tomography Model Combining Pixel-based and Function-based Models[J]. Advances in Space Research, 2013, 52(4): 614–621. DOI: 10.1016/j.asr.2013.05.003 |
| [2] | 李德仁, 苗前军, 邵振峰. 信息化测绘体系的定位与框架[J]. 武汉大学学报·信息科学版, 2007, 32(3): 189–192. |
| [3] | 李星星, 张小红, 李盼. 固定非差整数模糊度的PPP快速精密定位定轨[J]. 地球物理学报, 2012, 55(3): 833–840. |
| [4] | 张小红, 郭斐, 李盼, 等. GNSS精密单点定位中的实时质量控制[J]. 武汉大学学报·信息科学版, 2012, 37(8): 940–944. |
| [5] | 李征航, 何良华, 吴北平. 全球定位系统 (GPS) 技术的最新进展第二讲网络RTK[J]. 测绘信息与工程, 2002, 27(2): 22–25. |
| [6] | 田辉, 夏林元, 莫志明, 等. 泛在无线信号辅助的室内外无缝定位方法与关键技术[J]. 武汉大学学报·信息科学版, 2009, 34(11): 1372–1376. |
| [7] | Qian C, Ma J B, Ying R D, et al.An Improved Indoor Localization Method Using Smartphone Inertial Sensors[C].2013 International Conference on Indoor Positioning and Indoor Navigation, Montbéliard, France, 2013 |
| [8] | 徐亚明, 周建国, 张鹏. 一种WiFi无线接入点位置估计新算法[J]. 武汉大学学报·信息科学版, 2014, 39(3): 279–282. |
| [9] | Yang Y, Zhao Y B, Kyas M.A Grid-scan Maximum Likelihood Estimation with a Bias Function for Indoor Network Localization[C].2013 International Conference on Indoor Positioning and Indoor Navigation, Montbéliard, France, 2013 |
| [10] | Moghtadaiee V, Dempster A G.WiFi Fingerprinting Signal Strength Error Modeling for Short Distances[C].2012 International Conference on Indoor Positioning and Indoor Navigationm, Sydney, 2012 |
| [11] | Teramoto Y, Asahara A.Wireless LAN based Indoor Positioning Using Radio-Signal Strength Distribution Modeling[C].2012 International Conference on Indoor Positioning and Indoor Navigationm, Sydney, 2012 |
| [12] | Kula G, Ozyer T, Tavlib B. IEEE 802.11 WLAN Based Real Time Indoor Positioning:Literature Survey and Experimental Investigations[J]. Procedia Computer Science, 2014, 34: 157–164. DOI: 10.1016/j.procs.2014.07.078 |
 2017, Vol. 42
2017, Vol. 42

