| Leica AT960激光跟踪仪测量精度分析 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室, 湖北 武汉, 430079
2. Key Laboratory of Precise Engineer and Industry Surveying of National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China
激光跟踪测量系统(laser tracker system)是工业测量系统中一种高精度的大尺寸测量仪器。它集合了激光干涉测距技术、光电探测技术、精密机械技术、计算机及控制技术、现代数值计算理论等各种先进技术,对空间运动目标进行跟踪并实时测量目标的空间三维坐标。具有高精度、高效率、实时跟踪测量、安装快捷、操作简便等特点,适用于大尺寸工件配装测量。在测量领域, 因其高精度,激光跟踪仪的测量数据常常被作为检校其他测量设备精度的标准,激光跟踪仪测量精度与其标称精度的一致性直接决定了其数据结果的可靠性。因此对激光跟踪仪的实际测量精度进行分析是合理并且很有必要的。
国内外学者针对激光跟踪仪的精度分析开展了广泛的研究[1-4]。孙海丽等[5]以API公司的T3激光跟踪仪为例,通过对比、重复实验,对激光跟踪仪的精度进行了测量和验证。张三福[6]利用Leica AT401激光跟踪仪在某高速试验滑轨对接工房内,对激光跟踪仪进行了较全面的测试。欧阳健飞等[7]利用三坐标测量机建立虚拟三维网格标准球板来检验FARO激光跟踪仪的坐标测量精度。本文以Leica AT960激光跟踪仪为例,通过方向观测法、重复对比测量和自由设站等方式,在8 m×8 m×8 m的稳定且无遮挡的实验室内,对激光跟踪仪的测角、测距、点位坐标等精度进行了评定。
1 激光跟踪测量系统原理激光跟踪测量系统的基本原理是在目标点上安置一个反射器,跟踪头发出的激光射到反射器上,又返回到跟踪头,当目标移动时,跟踪头调整方向来对准目标。同时,返回光束为检测系统所接收,用来测算目标的空间位置。不同厂家生产的激光跟踪仪一般都由以下6个部分组成:激光测距系统(包括激光干涉测距装置和绝对测距装置等)、角度测量系统(包括水平和垂直的两个圆光栅环等)、跟踪控制系统、控制系统、跟踪目标(角隅棱镜反射球、T-Probe测头等)和仪器支撑部分。
激光跟踪测量系统本质上是一种球坐标测量系统(图 1)。它测量目标点的距离、水平和竖直方向的偏转角,从而得到以跟踪仪测量中心为原点的目标点空间三维坐标。
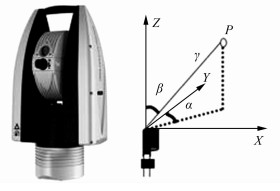 |
| 图 1 激光跟踪测量系统原理 Fig.1 Principle of Laser Tracking Measurement System |
激光跟踪仪利用激光干涉测距,测距精度很高,但激光本身受大气温度、压力、湿度及气流流动的影响,所以大气参数的补偿对此仪器的正常使用十分关键。
2 Leica AT960激光跟踪仪精度分析本文以Leica AT960激光跟踪仪为分析对象,其标称精度如表 1所示。
| 表 1 Leica AT960标称精度 Tab.1 Nominal Accuracy of Leica AT960 |
 |
2.1 测角精度分析
激光跟踪仪的测角误差来源一般可分为以下3类。
1) 激光跟踪仪测角度盘误差。目前市面上激光跟踪仪的测角系统一般采用光栅度盘,该测角传感器具有分辨率高、动态精度高、抗干扰信号能力强等优点,保证了激光跟踪仪测量的速度和精度。随着技术的发展,现在激光跟踪仪选用的光栅度盘精度越来越高,整个度盘的刻线数量也大大增加。与经纬仪的度盘偏心差类似,度盘刻线的不均匀性无法避免,将对测角系统产生误差,称为度盘分划误差,目前很难通过测量方法对该误差进行完全消除。
2) 激光跟踪仪轴系加工误差。激光跟踪仪不仅有水平轴和垂直轴,还有激光发射轴,这三轴与测角的两个度盘之间存在严格的理论关系。但是由于出厂时的制造差异、运输过程中发生的震动和碰撞以及实际测量环境的变化等因素,激光跟踪仪的三轴两盘之间的关系会与理论位置关系产生一定的偏差,从而产生测量误差。一般会将激光跟踪仪测角的全部系统误差分为15类,一共有15个校准参数[8],可以根据校准参数对结果进行修正,减弱这些系统误差的影响。同样,类似全站仪正倒镜观测法消除水平2C和垂直角指标差的影响,激光跟踪仪可以根据盘左盘右消除部分误差。
3) 大气折光误差。由激光跟踪仪的基本测量原理可知,激光跟踪仪的跟踪信号是通过反射的激光光束得到的,而激光通过大气时,大气折光会产生水平折光差和垂直折光差,对测角产生影响。
如图 2所示,为了验证激光跟踪仪的测角精度,选取实验室内大致处于同一高度的3个点P1、P2、P3,且3个点与仪器的距离近似相同。
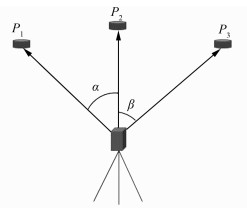 |
| 图 2 水平角观测示意图 Fig.2 Horizontal Angle Measurement |
对P1和P2之间的夹角α以及P2和P3之间的夹角β进行观测,方案如下:首先将靶球对准激光跟踪仪激光束发出的方向,将靶球置于P1进行观测,继续将靶球置于P2、P3方向进行观测,不断光的情况下连续观测10个测回,然后对观测数据进行处理。把每一个位置的角度值分别求平均,得到角度的改正数Δi,通过改正数求得水平角的中误差,中误差计算公式为:
| $ \hat \sigma = \sqrt {\frac{{\sum\limits_{i = 1}^n {\Delta _i^2} }}{{n - 1}}} $ | (1) |
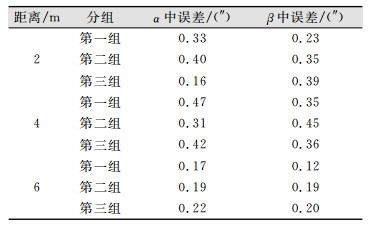
式中,Δi为改正数;n为观测次数。得到激光跟踪仪的水平角观测误差,如表 2所示。
| 表 2 激光跟踪仪水平角测角误差 Tab.2 Horizontal Angle Measurement Error of Laser Tracker |
 |
对仪器的水平角精度分析完成之后,再选取实验室内同一竖直平面内的多组点,进行垂直角精度的检定,如图 3所示。
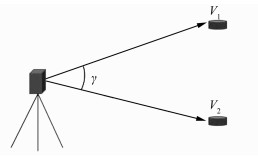 |
| 图 3 垂直角观测示意图 Fig.3 Vertical Angle Measurement |
选择上下两个点V1、V2,保证这两个点尽量在同一个竖直平面内,对V1、V2之间的夹角γ进行观测,测量方案如下:首先将靶球置于点V1进行观测,然后将靶球置于点V2进行观测,重复观测10次,为一组数据。选取另外相似的两组点,重复上述操作,对所得到的数据进行处理,处理方法同水平角误差分析,得到激光跟踪仪的水平角观测误差,如表 3所示。
| 表 3 激光跟踪仪垂直角测角误差 Tab.3 Vertical Angle Measurement Error of Laser Tracker |
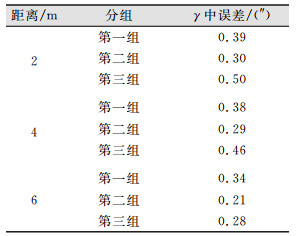 |
通过上述多组的测量,可以看出,激光跟踪仪的水平角和垂直角重复测角精度优于0.5″,均在其标称精度之内,符合其标称参数,其角度测量值是可靠的。
2.2 测距精度分析激光跟踪仪的测距系统包括激光干涉测距IFM(interferometer)和激光绝对测距ADM(absolute distance meter),测距误差一般来源于激光频率稳定性误差、校准参数误差与气象元素误差[9]。
为了对激光跟踪仪的实际测距精度进行验证,在实验室选取了近似与激光跟踪仪等高并且在同一条直线上的5个点S1、S2、S3、S4、S5,最大程度地减少水平角和垂直角测量的影响,如图 4所示。
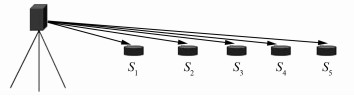 |
| 图 4 距离观测示意图 Fig.4 Distance Measurement |
第一组测量方法:将靶球置于基座上,连续测量20次,再转入下一点测量;
第二组测量方法:将靶球置于基座上,读完一个数后,将靶球拿起,重新放置靶球并测量,对同一点测量20次。两组测量均保证整个实验过程不断光,连续观测20个测回,否则全部重新进行测量,然后进行数据处理,得到两组距离观测值的处理结果, 如表 4所示。
| 表 4 激光跟踪仪测距精度/±μm Tab.4 Ranging Accuracy of Laser Tracker/±μm |
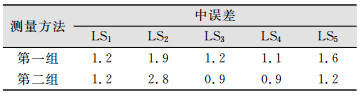 |
通过上述多组的测量可以看出,在稳定的条件下,激光跟踪仪的重复测距精度在其标称精度10 μm之内,符合其标称参数,其距离测量值精度较高并且可靠。
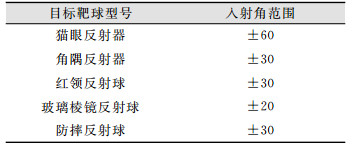
2.3 激光入射角精度分析激光跟踪仪在测量目标靶球时,激光的入射角也会对测量带来误差。目前使用的目标靶球一般有猫眼反射器、角隅棱镜反射器、玻璃棱镜反射球和防摔反射球等几种类型。本次测量使用的是防摔反射球,其入射角技术参数如表 5所示。
| 表 5 目标靶球及其入射角范围/(°) Tab.5 Incident Angle Range of Target Ball/(°) |
 |
为了测试激光相对于靶球的入射角对测量带来的影响,利用Leica AT960激光跟踪仪和防摔反射球(BRR)进行了实验。考虑到BRR的最大入射角为±30°,选取地面上一固定位置,第一组将目标靶球放置在基座上,挪动靶球,对准激光入射方向,连续测量20次;第二组将靶球球面绕激光入射轴逆时针旋转30°,连续测量20次;第三组将靶球球面绕激光入射轴顺时针旋转30°,连续测量20次;得到测量中误差, 如表 6所示。
| 表 6 不同入射角下的测量中误差 Tab.6 Measurement Error at Different Incident Angles |
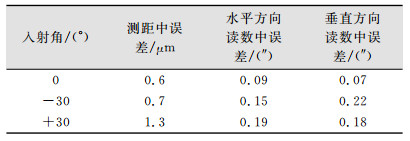 |
从表 6可以看出,目标靶球在允许的入射角范围内,测角测距精度与激光的入射角有关。当靶球朝向过偏时,激光跟踪仪发出的激光光束将不再在靶球中心汇聚成一点,造成测量误差。因此在实际测量中,尽量保证目标靶球和仪器保持正对关系,减少入射角带来的测量误差。
2.4 环境因素引入的测量误差大气的光照不一致、环境温度不稳定、风力影响下的空气震动等因素会引起折光差,从而产生测量误差。利用不同环境条件下的同一靶球重复测量读数对这一误差进行了验证分析。将靶球置于一固定且稳定的基座上,整个测量过程中,保证靶球底座固定不动,仪器周围没有人员走动,对靶球进行测量,连续观测20次,并重复3组;然后打开空调,在有风且温度湿度变化的情况下,对同一靶球进行同样的观测;根据得到的数据求出各观测值均值和偏差,利用式(2)求出中误差,如表 7所示。
| 表 7 环境因素引起的测量中误差 Tab.7 Measurement Error of Envirnmental |
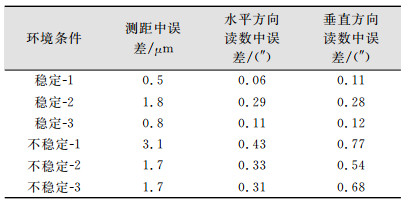 |
从表 7可以看出,在气象条件改变至不稳定状态的时候,激光跟踪仪的测量误差会明显增大,由此可见,环境的随机误差也是测量中一个不可忽视的误差源。虽然在实际测量中,激光跟踪仪内置的气象传感器会实时采集测量环境的温度、大气压和湿度等气象参数,对观测值进行修正,但是从理论上分析,大气折射率在激光光路上不一致,准确值应该由对光路方向进行积分得到,实际是将测站的气象参数代替整个光路进行修正,仍会存在一定的误差。因此在实际测量中,应该尽量保证环境温度、风力、大气压和湿度等气象条件比较稳定。避免由周围环境人员走动、阳光照射不均匀等环境条件造成的随机误差。
3 点位坐标精度分析点位坐标的精度也是衡量仪器测量精度的一个重要指标[10, 11],能够比较具有代表性地反应在实际的测量过程中由各种误差因素综合引起的点位误差。
在实际测量过程中,一般需要多次设站完成整个测量,这就需要设置不少于3个公共点来完成转站。假设整个系统处于理想状态,将不同测站观测的一组公共点归算到统一的坐标系后,坐标值应相同,但是实际测量结果并不相同,这种情况是由现场所有测量条件引起的,包括仪器本身测角测距误差、环境误差、人员操作误差及转站误差等。文献[12]提出了一种基于均方根误差的精度分析,即对一组公共点进行多次移站测量,分析各点在统一坐标系下的变化量来评定仪器现场测量的点位坐标重复测量精度。
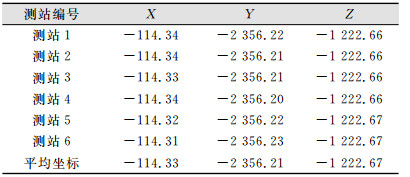
如图 5所示,首先在测量空间选了6个公共点,分别在6个不同的测站对公共点进行了重复观测。利用SA软件的最佳拟合转化,将不同测站下的各点转化到同一坐标系下,并得到各个点转化后在同一坐标系下的坐标数据, 表 8为1号点在各个测站下的观测值转化到同一个坐标系下的坐标。
 |
| 图 5 公共点转站观测示意图 Fig.5 Transfer Station Measurement of Common Point |
| 表 8 1号点转化后的坐标/mm Tab.8 Converted Coordinates of Point 1/mm |
 |
假设对于其中某一公共点,坐标转化后得到各点分别为p1、p2,…,pn,求出其平均坐标点
| $ {\rm{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {d_i^2} } $ | (2) |
扩展到m个点n个测站,可表示为:
| $ {\rm{RMSE}} = \sqrt {\frac{1}{{m \times n}}\sum\limits_{i = 1}^m {\left( {\sum\limits_{j = 1}^n {d_j^2} } \right)} } $ | (3) |
根据式(2)求出各个点在多个测站下的均方根误差,如表 9所示。
| 表 9 各个点RMSE值/μm Tab.9 RMSE Value of Each Point/μm |
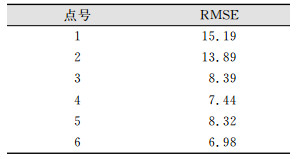 |
根据式(3),整个测量系统的均方根误差为10.5 μm。因此,各个点在不同测站下的点位坐标重复测量精度为10.5 μm,符合其标称精度。
4 结束语本文简要介绍了激光跟踪仪的现状和基本原理,列出了目前国内外常用的激光跟踪仪精度检定的方法;并且基于Leica AT960激光跟踪仪,详细地分析了激光跟踪仪的测角、测距及点位坐标误差,给出了具体的精度验证结果,在实验室环境下,角度重复测量精度优于0.5″,距离重复测量精度优于3 μm,现场点位重复测量精度可达到10.5 μm,均在标称精度范围内,测量精度高且具有较高的可靠性。
| [1] |
于成浩, 柯明, 赵振堂. 激光跟踪仪测量精度的评定[J]. 测绘工程, 2006(6): 39-42. DOI:10.3969/j.issn.1006-7949.2006.06.011 |
| [2] |
赵树忠.提高激光跟踪三维坐标测量精度的研究[D].天津: 天津大学, 2007 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1361907
|
| [3] |
张福民, 曲兴华, 叶声华. 面向对象的大尺寸测量不确定度分析[J]. 光学精密工程, 2008(11): 2239-2243. DOI:10.3321/j.issn:1004-924X.2008.11.033 |
| [4] |
杨占立, 范百兴, 西勤, 等. 基于空间平面TLS算法的跟踪仪动态测量精度分析[J]. 测绘地理信息, 2017, 42(5): 42-45. |
| [5] |
孙海丽, 姚连璧, 周跃寅, 等. 激光跟踪仪测量精度分析[J]. 大地测量与地球动力学, 2015, 35(1): 177-181. |
| [6] |
张三福.基于激光跟踪仪的精密控制网建立及其精度分析研究[D].兰州: 兰州交通大学, 2014 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D539706
|
| [7] |
欧阳健飞, 刘万里, 闫勇刚, 等. 激光跟踪仪坐标测量精度的研究[J]. 红外与激光工程, 2008, 37(S1): 15-18. |
| [8] |
李广云. LTD500激光跟踪测量系统原理及应用[J]. 测绘工程, 2001(4): 3-8. DOI:10.3969/j.issn.1006-7949.2001.04.001 |
| [9] |
Ren Y, Lin J R, Sun B, et al. Coordinate Transformation Uncertainty Analysis in Large-Scale Metrology[J]. IEEE Transactions on Instrumentation and Measurement, 2015, 64(9): 2380-2388. DOI:10.1109/TIM.2015.2403151 |
| [10] |
刘新宇. 大尺寸结构件检测方法研究及不确定度分析[J]. 航空制造技术, 2015(7): 76-79. |
| [11] |
金涨军, 李江雄, 俞慈君, 等. 大尺寸空间测量中转站误差分析与估计[J]. 浙江大学学报(工学版), 2015, 49(4): 655-661. |
| [12] |
张春富, 张军, 许文海, 等. 激光跟踪仪现场测量不确定度的评定[J]. 计量学报, 2005(1): 20-22. DOI:10.3321/j.issn:1000-1158.2005.01.006 |
 2020, Vol. 45
2020, Vol. 45

