| 随机性非等间隔灰色模型在沉降预报中的应用 |
2. 湖南科技大学资源环境与安全工程学院,湖南 湘潭,411201
2. School of Resource and Environment and Safety Engineering, Hunan University of Science and Technology, Xiangtan 411201, China
在现代测量工作中,变形监测已经成为不可或缺的重要部分。尤其是城市地铁建设的崛起,地铁在隧道开挖过程中会导致沿线地面发生不均匀下沉,大部分地铁线路都会穿越城市中心的繁华地带,并且隧道的埋深较浅,与城市地下的密集管线会有交集,其变形过大必然会导致隧道上部的设施面临损坏的危险,其影响不容小视。因此,更加需要精密的监测、科学的分析以及准确的预报。
目前,地层位移预测的主要方法有经验公式、数值模拟、模型试验研究、专家系统和灰色理论等[1]。经验公式法被广泛应用于早期的地表移动变形预测中,其中以随机介质理论为基础建立的Peck模型最佳,并被工程实践所验证[2]。数值模拟法是隧道施工地层移动变形预测中最常用的方法,先用实测数据辅助构建三维数值模型,再模拟整个施工过程,并指导各施工工序[3]。随着测量手段和技术的提升,模型试验研究从早期的相似材料模型发展到了离心试验模型以及有机玻璃盾构模型等方法,为盾构施工引起的地层移动问题的研究提供了可靠的数据支撑[4, 5]。神经网络作为专家系统的代表方法之一,优势包括自适应能力强、学习和容错能力强,利用神经网络技术可以处理非线性问题,该方法处理非结构型规律的多因素综合影响问题的适应性更强[6]。神经网络方法最大的不足是预测性能受样本集影响,所以其研究方向是将神经网络与专家系统的优势集成互补,如协同式的神经网络专家系统。
使用这些方法时,要建立一定的模型进行预测,部分学者根据不同建模方法的特点将其应用到具体的工程实例中,都取得了不错的预测效果[7-11]。其中,灰色理论是近年来的热点研究课题,它通过已有数据列求取所建微分方程的参数,建立灰色预测基本模型。关于等间隔灰色模型的研究较为成熟,其建模方法有十余种。但对于非等间隔模型,尤其是关于强、弱随机性非等间隔灰色模型的对比及适用条件的研究较少[12-15]。强、弱随机性非等间隔灰色模型通过引入单位时间系数差来调整不等间隔序列与等间隔序列的差别,对差值部分进行单独累加并叠加建模,提高模型的使用范围、预测步长和精度。在地铁隧道施工过程中,由于施工原因,经常出现获取的变形监测数据是非等间隔的。针对此问题,本文利用隧道拱顶和地表沉降序列数据建立强、弱随机性非等间隔灰色预测模型,同时分析了原始数据的沉降趋势。对预测精度和非等间隔点所处的沉降趋势阶段进行分析,结果表明,这两种建模方法仅适用于隧道拱顶的变形沉降预测,且强随机性模型的预测效果要比弱随机性模型的预测效果好。
1 非等间隔序列的数列预测 1.1 弱随机性非等间隔序列的数列预测设非等间隔原始数列X(0)=(x(0)(1),x(0)(2),···,x(0)(n)),弱随机性非等间隔序列的数列预测步骤如下:
1)求平均时间间隔Δt:
| $ \Delta t=\frac{1}{n-1} \sum\limits_{i=1}^{n-1} \Delta t_{i}=\frac{1}{n-1}\left(t_{n}-t_{1}\right) $ | (1) |
2)求单位时段差系数u(ti):
| $ u\left(t_{i}\right)=\frac{t_{i}-(n-1) \Delta t_{0}}{\Delta t_{0}}, i \in\{1, 2, \cdots, n\} $ | (2) |
3)求各时段总的差值Δx1(0):
| $ \Delta x_{1}^{(0)}\left(t_{i}\right)=u\left(t_{i}\right)\left[x_{1}^{(0)}\left(t_{i+1}\right)-x_{1}^{(0)}\left(t_{i}\right)\right] $ | (3) |
4)求等间隔点的灰数值
| $ \otimes i=x_{1}^{(0)}\left(t_{i}\right)-\Delta x_{1}^{(0)}\left(t_{i}\right), i \in\{1, 2, \cdots, n\} $ | (4) |
于是得到如下等间隔序列:
| $ \otimes X_{2}^{(0)}(t)=\left\{X_{2}^{(0)}(1), \cdots, X_{2}^{(0)}(t)\right\} $ | (5) |
5)对
| $ \hat{x}_{2}^{(1)}(k+1)=\left(x_{2}^{(0)}(1)-\frac{u}{a}\right) \mathrm{e}^{-a k}+\frac{u}{a} $ | (6) |
式中,k = 1,2,···,n,表示表示序列次序;a、u表示表示一阶微分方程的参数。
6)模型精度检验及预测。
将非等间隔序列中原始数据的时间t代入式(6),求得原始数据的预测值,并求取残差及相对误,再按后验差检验法进行精度检验。
1.2 强随机性非等间序列的数列预测强随机性非等间序列的数列预测的前3个步骤同弱随机性非等间序列的相同。
1)求平均时间间隔Δt。
2)求单位时段差系数u(ti)。
3)求各时段总的差值Δx1(0)。
4)对Δx1(0)进行1次累加生成(1-accumulated generating operation,1-AGO),可得:
| $ \Delta X^{(1)}(t)=\left\{\Delta x^{(1)}(1), \cdots, \Delta x^{(1)}(n)\right\} $ | (7) |
5)求ΔX(1)(t)的均值数列:
| $ \left\{\begin{array}{l} \Delta \bar{x}^{(1)}(t)=\frac{1}{2}\left(\Delta x^{(1)}(t)+\Delta x^{(1)}(t-1)\right) \\ \Delta \bar{X}^{(1)}(t)=\left\{\Delta \bar{x}^{(1)}(1), \cdots, \Delta \bar{x}^{(1)}(n)\right\} \end{array}\right. $ | (8) |
6)对原始数列X(0)(t)作1-AGO,可得:
| $ X^{(1)}(t)=\left\{x^{(1)}(1), x^{(1)}(2), \cdots, x^{(1)}(n)\right\} $ | (9) |
7)求x(1)(t)的均值数列:
| $ \left\{\begin{array}{l} \bar{X}^{(1)}(t)=\frac{1}{2}\left(x^{(1)}(t)+x^{(1)}(t+1)\right) \\ \bar{X}^{(1)}(t)=\left\{\bar{x}^{(1)}(1), \bar{x}^{(1)}(2), \cdots, \bar{x}^{(1)}(n)\right\} \end{array}\right. $ | (10) |
8)计算各等间隔点的灰数值
| $ \otimes \bar{X}^{(1)}(t)=\bar{x}^{(1)}(t)+\Delta \bar{x}^{(1)}(t) $ | (11) |
9)求斜率(常数项)的差值,即按照非等间隔与等间隔曲线相差一个相角
| $ \left\{\begin{array}{l} \otimes \Delta \alpha_{i} \approx \partial(i) \frac{u\left(t_{i}\right)}{x^{(0)}\left(t_{i}\right)}\left(1+u\left(t_{i}\right)\right) \\ \partial(i)=\frac{x^{(0)}\left(t_{i}+1\right)-x^{(0)}\left(t_{i}\right)}{\left|x^{(0)}\left(t_{i}+1\right)-x^{(0)}\left(t_{i}\right)\right|} \end{array}\right. $ | (12) |
式中,∂(i)表示白化改正符号;i为序列号,当序列值减小时,∂(i)=-1,反之,∂(i)=+1。因此可得:
| $ \frac{\mathrm{d} \otimes x^{(1)}}{\mathrm{d} t}=\frac{\mathrm{d} x^{(1)}}{\mathrm{d} t}+\partial \frac{u}{x^{(0)}(t)}(1+u) $ | (13) |
10)建模。由以上可知一阶微分方程为:
| $ \frac{\mathrm{d} \bar{x}^{(1)}}{\mathrm{d} t}+\partial \frac{u}{x^{(0)}(t)}(1+u)+a\left(\bar{x}^{(1)}\left(t_{i}\right)\right.+\Delta \bar{x}^{(1)}\left(t_{i}\right)=u $ | (14) |
式中,â=[a u]T,计算公式如下:
| $ \hat{\boldsymbol{a}}=\left[\begin{array}{ll} a & u \end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ll} \boldsymbol{B}^{\mathrm{T}} & \boldsymbol{B} \end{array}\right]^{-1} \boldsymbol{B}^{\mathrm{T}} \boldsymbol{y}_{n} $ | (15) |
式中,
解得时间响应函数:
| $ \left\{\begin{array}{l} \hat{x}^{(1)}(t)=\left(x^{(0)}(1)-\frac{u}{a}\right) \mathrm{e}^{-a t / \Delta t_{0}}+\frac{u}{a} \\ \hat{x}^{(0)}(t)=\hat{x}^{(1)}(t)-\hat{x}^{(1)}\left(t-\Delta t_{0}\right) \end{array}\right. $ | (16) |
11)模型精度检验及预测。
2 算例分析本文选择深圳市地铁九号线某渡线隧道拱顶点和地表的沉降累计值作为建模的原始数据。这两处地点分别代表了地铁隧道内、外的两种不同监测数据(拱顶点为洞口位置沉降最大的位置,地表点位于地表沉降最大的断面上),具有一定的代表性。渡线隧道施工监测图见图 1。选取部分时段内的两组观测数据作为原始数据进行实验,分别为隧道拱顶:GZD1(共45期)、GD2(共66期);隧道地表:SE4(共67期)、EL3(共67期)。本文随机选择其中的15期数据作为非等间隔预测的建模数据,如表 1所示,后11期数据作为预测数据,如表 2所示。
 |
| 图 1 渡线隧道施工监测图 注:单位m。 Fig.1 Construction Monitoring Diagram of Connecting Tunnel |
| 表 1 建模数据信息 Tab.1 Information of Modeling Data |
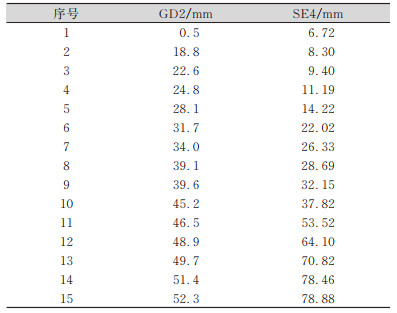 |
| 表 2 预测数据信息 Tab.2 Information of Predicted Data |
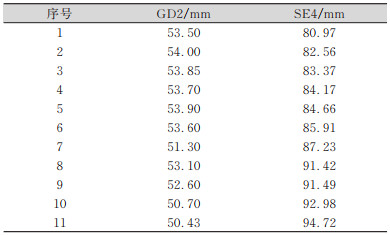 |
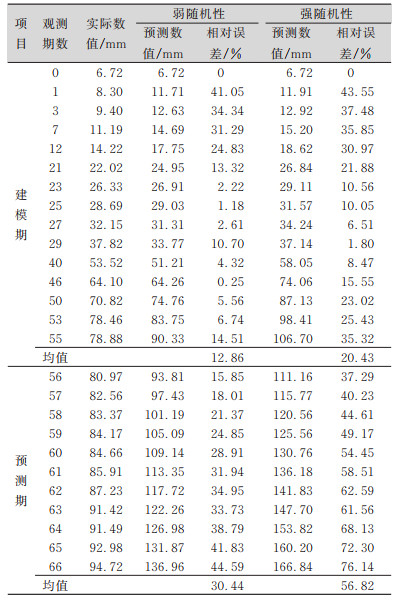
对GD2及SE4点数据进行数据处理后,可得到表 3和表 4所示的成果。利用同样的方法对4组数据进行处理,可得到强、弱随机性非等间隔灰色模型的对比分析结果,如表 5所示。分析可得出如下结论:
| 表 3 隧道拱顶点GD2的强弱随机性模型变形预测值 Tab.3 Predicted Deformation Values of Vault Point (GD2)Obtained by Strong and Weak Randomness Models |
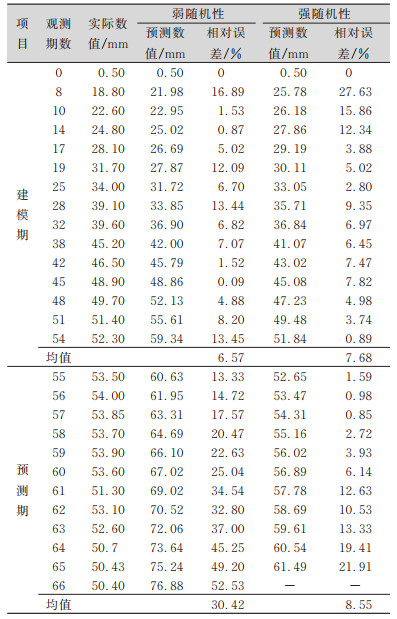 |
| 表 4 隧道地表点SE4的强弱随机性模型变形预测值 Tab.4 Predicted Deformation Values of of Ground Point (SE4)Obtained by Strong and Weak Randomness Models |
 |
| 表 5 4组数据处理结果对比 Tab.5 Comparison of the Results of Four Group Data |
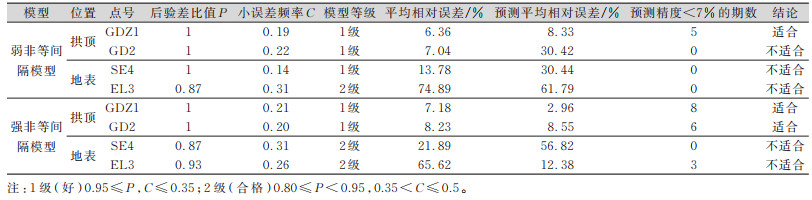 |
1)对于隧道拱顶的变形预测,强、弱随机性非等间隔序列模型都适合,且强随机性非等间隔序列模型的预测精度比弱随机性模型的建模精度好。
2)对于隧道地表的变形预测,两种模型都不适合,建模精度差,预测精度也差。
3)在数据呈现出两阶段的变形特点时,强随机性非等间隔序列模型的预测效果比弱随机性非等间隔序列模型的预测效果好,且预测步长更长。
一般来说,模型的选取与数据的变化趋势有很大的关系。因此,对隧道拱顶及隧道地表数据分别进行绘图处理,可得到图 2和图 3,分析可得,数据变化趋势如下:①隧道拱顶点GZD1呈一阶段变化趋势,即平缓上升趋势,但上升幅度逐渐变小;隧道拱顶点GD2分为两个阶段:上升幅度逐渐减小的平缓上升阶段以及趋于平稳甚至出现下降趋势的阶段。②隧道地表数据SE4与EL3趋于一致,其变化趋势分为3个阶段:增幅极为缓慢的缓慢增长阶段、增幅极大的加速增长阶段、增幅逐渐减少的平缓增长阶段。
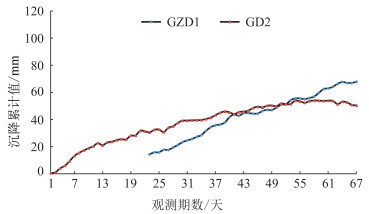 |
| 图 2 隧道拱顶点GZD1、GD2的累计沉降值 Fig.2 Accumulated Settlement Values of Tunnel Vault Points(GZD1 and GD2) |
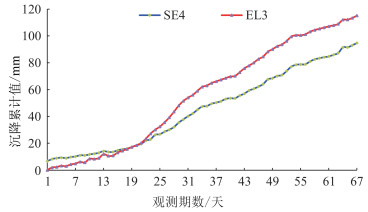 |
| 图 3 隧道地表点SE4、EL3的累计沉降值 Fig.3 Accumulated Settlement Values of Ground Points (SE4 and EL3) |
分析数据结果与数据变化趋势,可得如下结论:
1)对于该工程的隧道拱顶累计沉降量处于一阶段变化(即缓慢上升阶段,如GZD1)的预测中,强、弱随机性非等间隔模型均可进行预测,但强随机性非等间隔模型比弱随机性模型的预测精度要高,预测步长更长,当预测步数≥8时,强随机模型的精度仍能达到2.96%,这个精度完全满足施工的要求。
2)对于该工程的隧道拱顶累计沉降量处于两个阶段(即缓慢上升阶段和趋于稳定阶段,如GD2)的预测中,强、弱随机性非等间隔模型的预测精度比处于一个阶段的预测精度有所降低,且弱随机性非等间隔模型不很适合两阶段的预测,预测效果较差。
3)对于该工程的隧道地表累计沉降量处于3个阶段(即增长阶段、减速增长阶段及平缓增长阶段,如SE4、EL3)的预测中,强、弱随机性非等间隔模型均不适于进行预测,预测精度较差,通过计算验证了其正确性。
3 结束语本文以实测渡线隧道拱顶和地表沉降为数据源,通过对其分别建立强、弱随机性灰色预计模型,并通过MATLAB编程对比分析程序输出的模型精度和预测精度,得出了强随机性更适合对隧道拱顶非等间隔监测数据的建模预报。通过进一步分析原始数据的沉降趋势,建立数据的增减趋势与预测模型的选取关系:对于沉降处于缓慢上升阶段的数据列,强弱随机性预测模型均可;先缓慢上升再趋于稳定的数据列,强随机性可以但弱随机性模型不适合;而对于沉降变形先增长、再减缓最后平稳的数据列,强弱随机性模型的预测结果都很差。这个结论为以后更加准确合理的使用非等间隔灰色预计模型提供参考,也对以后准确的预计拱顶沉降和保证地铁隧道的施工安全具有一定的实践参考价值。
| [1] |
牛学军. 城市地铁盾构施工测量若干问题的探讨[D]. 武汉: 武汉大学, 2005
|
| [2] |
施成华, 彭立敏, 刘宝琛. 盾构法施工隧道纵向地层移动与变形预计[J]. 岩土工程学报, 2003, 25(5): 585-589. DOI:10.3321/j.issn:1000-4548.2003.05.015 |
| [3] |
张昊, 王虎. 盾构隧道施工引起的地层移动有限元分析: 以苏通GIL综合管廊隧道南岸施工为例[J]. 现代隧道技术, 2018, 55(S2): 909-915. |
| [4] |
孙吉主, 肖文辉. 盾构模型试验研究现状及新设想[J]. 土工基础, 2011, 25(6): 49-52. DOI:10.3969/j.issn.1004-3152.2011.06.015 |
| [5] |
朱训国, 陈枫, 徐孟林, 等. 大连地铁盾构开挖地层移动规律的模型试验研究[J]. 岩土力学, 2013, 34(S1): 148-154. |
| [6] |
王利丰, 孙树林, 曹继平. 盾构施工引起地表变形的人工神经网络研究[J]. 地下空间与工程学报, 2005, 1(5): 761-764. |
| [7] |
王敬宾, 杨永新, 梁丽娟. 经验公式法预测砂岩高速铁路路基沉降[J]. 内蒙古科技大学学报, 2014, 33(3): 295-298. DOI:10.3969/j.issn.2095-2295.2014.03.020 |
| [8] |
黄合理. 地铁隧道穿越既有车站的沉降预测及加固措施[J]. 现代隧道技术, 2013, 50(2): 114-118. DOI:10.3969/j.issn.1009-6582.2013.02.018 |
| [9] |
潘孝良. 浅谈模型试验法的理论与应用(续)[J]. 山东建材学院学报, 1987, 1(2): 1-3. |
| [10] |
张煜东, 吴乐南, 王水花. 专家系统发展综述[J]. 计算机工程与应用, 2010, 46(19): 43-47. DOI:10.3778/j.issn.1002-8331.2010.19.012 |
| [11] |
傅立. 灰色系统理论及其应用[M]. 北京: 科学技术文献出版社, 1992.
|
| [12] |
邹进贵, 聂海滨, 邱国庆. 一种同时优化背景值和初始条件的GM(1, 1)建模方法[J]. 测绘地理信息, 2018, 43(2): 79-82. |
| [13] |
范献胜. 非等间隔灰色模型的稳定性和病态性研究[D]. 武汉: 武汉理工大学, 2013
|
| [14] |
骆汉宾, 李炜明, 周光辉. 武汉地铁盾构施工地表沉降的非等间隔模型分析[J]. 铁道工程学报, 2011, 28(1): 86-91. |
| [15] |
赵磊磊, 花向红, 邵梽, 等. 改进的新陈代谢GM(1, 1) 模型在建筑物沉降预测中的应用[J]. 测绘地理信息, 2019, 44(6): 120-122. |
 2022, Vol. 47
2022, Vol. 47

