| 基于LRO测高数据和GRAIL重力数据解算的月球三轴椭球体模型 |
2. 中国南极测绘研究中心,武汉大学,430079;
3. 测绘遥感信息工程国家重点实验室,武汉大学,430079)
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, 430079;
3. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, 430079
已有结果表明:月球的三个主惯性矩并不相等,即月球实际上是一个三轴体而非球体。因此,建立与月球实际形状和物理特性更为符合的三轴参考体是必要的。
研究月球形状参数的方法主要有球谐函数法和椭球体拟合法。球谐函数法求解月球半径等参数时,模型截止阶次对数据精度的影响很大。为了避免截止阶次的影响,本文选用椭球体拟合的方法求解月球的三轴椭球体[1]。
针对三轴椭球体,国内外已有不少研究[1-3]。最新公布的高精度高分辨LRO(lunar reconnaissance orbiter)测高数据和GRAIL(gravity recovery and interior laboratory)重力数据,为进一步精确建立三轴椭球体模型提供了有利条件。根据LRO已有的测高数据解算得到的地形模型空间分辨率为100 m,为目前分辨率最高的地形模型[4]。GRAIL提供了精度更高、分布更均匀的跟踪数据,根据GRAIL 正常任务阶段前3个月的星间跟踪数据,JPL和Goddard分别解算了660阶次模型GL0660B和GRGM660PRIM,模型精化了全球重力信息,极大程度地改进了月球重力场的精度和分辨率。
1 三轴几何椭球体模型建立为了得到更符合月球实际地形的形状中心与质量中心的偏移量,在拟合最逼近月球表面地形的几何体时,将形心坐标系原点相对于质心坐标系的偏移量(x0,y0,z0)作为未知量同时求解椭球体的三条主轴长(a,b,c)[1]。如图 1所示,O-XYZ是以质心为原点的惯性坐标系;o-xyz为形心坐标系,oz与月球自转轴平行,o在O-XYZ中的坐标为形心相对于质心的偏移量。
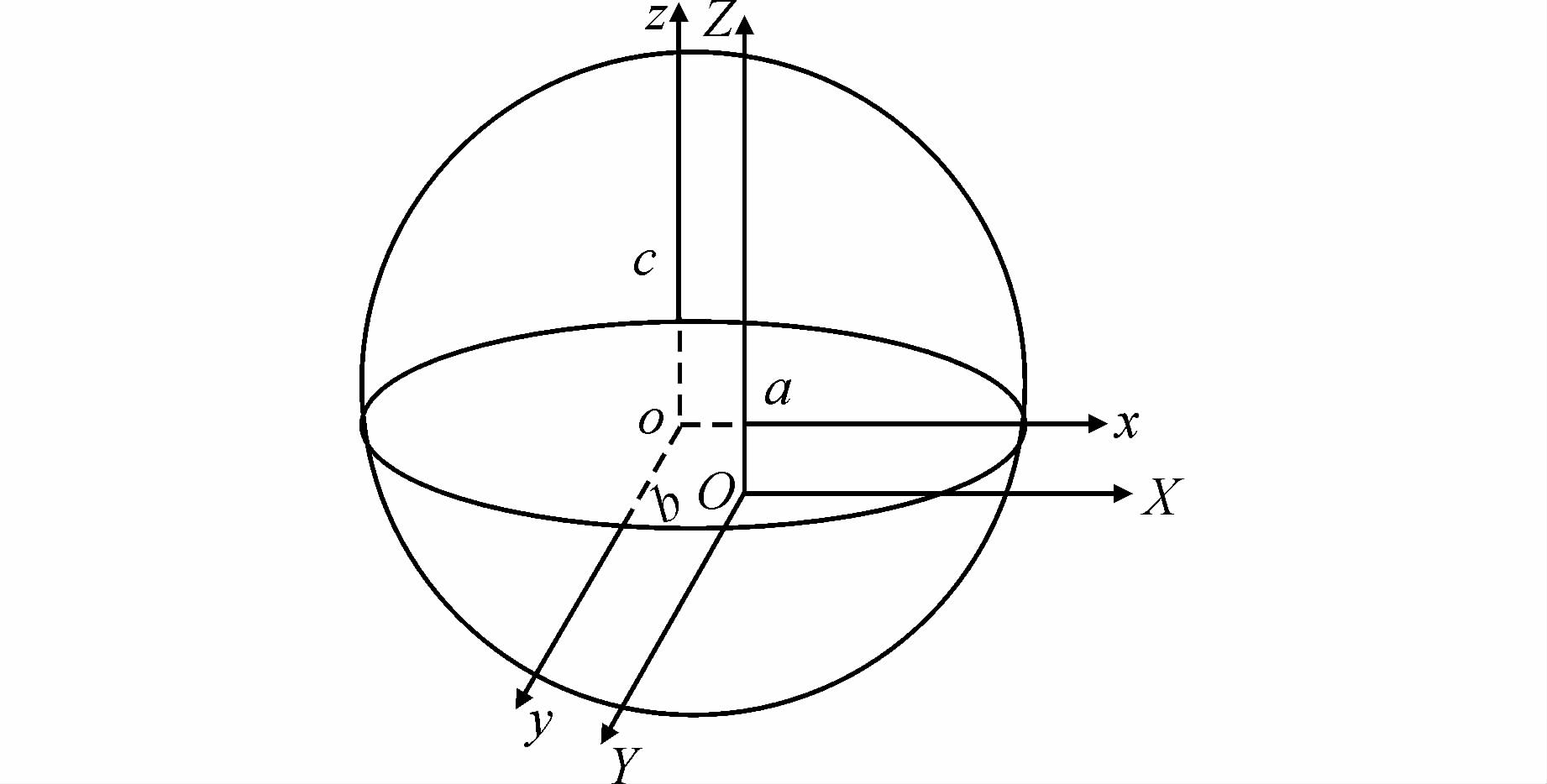 |
| 图 1 三轴几何椭球体示意图 Figure 1 Sketch Map of Tri-axial Geometric Ellipsoid |
利用拟合椭球法构建最逼近月表地形的三轴几何椭球体条件方程为:
| ${{\left( \frac{x-{{x}_{0}}}{aa} \right)}^{2}}+{{\left( \frac{y-{{y}_{0}}}{bb} \right)}^{2}}+{{\left( \frac{z-{{z}_{0}}}{cc} \right)}^{2}}-1=\min $ | (1) |
式中,(x,y,z)为月表观测点在月球质心参考框架中的坐标; a、b、c为待求椭球体的半轴长; (x0,y0,z0)为形心坐标系原点在质心坐标系中的坐标。
计算过程为:①将地形模型格网数据转换成月球质心坐标系下的直角坐标:
| $\left\{ \begin{matrix} x=(h+r)cos\varphi cos\lambda \\ y=(h+r)cos\varphi \sin \lambda \\ z=(h+r)\sin \varphi \\ \end{matrix} \right.$ | (2) |
式中,(x,y,z)为星下点在月球质心坐标系中的直角坐标值; h为观测星下点在对应高程基准下的高程值; r为球形基准半径; φ、λ分别为月心坐标系下星下点纬度值、经度值。
②将平坐标系下的测高数据转换到主轴坐标系下[5],作为原始输入数据,采用间接平差的方法,可以得到:
| $X={{\left( {{A}^{T}}PA \right)}^{-1}}\left( {{A}^{T}}PB \right)$ | (3) |
其中,椭球体参数系数矩阵为:
| $\begin{align} & A=\left[ \begin{matrix} {{a}_{1}} & {{a}_{2}} & {{a}_{3}} & {{b}_{1}} & {{b}_{2}} & {{b}_{3}} \\ \end{matrix} \right] \\ & \left[ \begin{matrix} \frac{{{x}_{1}}-{{{\hat{x}}}_{0}}}{{{a}^{2}}}+\frac{{{y}_{1}}-{{{\hat{y}}}_{0}}}{{{b}^{2}}}+\frac{{{z}_{1}}-{{{\hat{z}}}_{0}}}{{{c}^{2}}}\frac{{{\left( {{x}_{1}}-{{{\hat{x}}}_{0}}^{2} \right)}^{2}}}{{{a}^{3}}}\frac{\left( {{y}_{1}}-{{{\hat{y}}}_{0}}^{2} \right)}{{{b}^{3}}}\frac{\left( {{z}_{1}}-{{{\hat{z}}}_{0}}^{2} \right)}{{{c}^{3}}} \\ \frac{{{x}_{2}}-{{{\hat{x}}}_{0}}}{{{a}^{2}}}+\frac{{{y}_{2}}-{{{\hat{y}}}_{0}}}{{{b}^{2}}}+\frac{{{z}_{2}}-{{{\hat{z}}}_{0}}}{{{c}^{2}}}\frac{{{\left( {{x}_{2}}-{{{\hat{x}}}_{0}}^{2} \right)}^{2}}}{{{a}^{3}}}\frac{\left( {{y}_{2}}-{{{\hat{y}}}_{0}}^{2} \right)}{{{b}^{3}}}\frac{\left( {{z}_{2}}-{{{\hat{z}}}_{0}}^{2} \right)}{{{c}^{3}}} \\ \vdots \\ \frac{{{x}_{n}}-{{{\hat{x}}}_{0}}}{{{a}^{2}}}+\frac{{{y}_{n}}-{{{\hat{y}}}_{0}}}{{{b}^{2}}}+\frac{{{z}_{n}}-{{{\hat{z}}}_{0}}}{{{c}^{2}}}\frac{{{\left( {{x}_{n}}-{{{\hat{x}}}_{0}}^{2} \right)}^{2}}}{{{a}^{3}}}\frac{\left( {{y}_{n}}-{{{\hat{y}}}_{0}}^{2} \right)}{{{b}^{3}}}\frac{\left( {{z}_{n}}-{{{\hat{z}}}_{0}}^{2} \right)}{{{c}^{3}}} \\ \end{matrix} \right] \\ \end{align}$ | (4) |
观测矩阵为:
| $B=\frac{1}{2}\left[ \begin{matrix} {{\left( \frac{{{x}_{1}}-{{{\hat{x}}}_{0}}}{{{a}^{2}}} \right)}^{2}}+{{\left( \frac{{{y}_{1}}-{{{\hat{y}}}_{0}}}{{{b}^{2}}} \right)}^{2}}+{{\left( \frac{{{z}_{1}}-{{{\hat{z}}}_{0}}}{{{c}^{2}}} \right)}^{2}}-1 \\ {{\left( \frac{{{x}_{2}}-{{{\hat{x}}}_{0}}}{{{a}^{2}}} \right)}^{2}}+{{\left( \frac{{{y}_{2}}-{{{\hat{y}}}_{0}}}{{{b}^{2}}} \right)}^{2}}+{{\left( \frac{{{z}_{2}}-{{{\hat{z}}}_{0}}}{{{c}^{2}}} \right)}^{2}}-1 \\ \vdots \\ {{\left( \frac{{{x}_{n}}-{{{\hat{x}}}_{0}}}{{{a}^{2}}} \right)}^{2}}+{{\left( \frac{{{y}_{n}}-{{{\hat{y}}}_{0}}}{c} \right)}^{2}}+{{\left( \frac{{{z}_{n}}-{{{\hat{z}}}_{0}}}{{{c}^{2}}} \right)}^{2}}-1 \\ \end{matrix} \right]$ | (5) |
未知量矩阵为:
| $X={{\left[ \begin{matrix} \Delta {{x}_{0}} & \Delta {{y}_{0}} & \Delta {{z}_{0}} & \Delta a & \Delta b & \Delta c \\ \end{matrix} \right]}^{T}}$ | (6) |
初始未知量的选取如下:
| ${{\rho }_{S}}={{R}_{0}}\left[ \sum\limits_{l=0}^{N}{\sum\limits_{m=0}^{l}{{{P}_{lm}}(sin\varphi )\left( {{C}_{lm}}\cos m\lambda +{{S}_{lm}}\sin m\lambda \right)}} \right]$ | (7) |
根据上述算法建立月球三轴几何椭球体的流程如图 2所示。
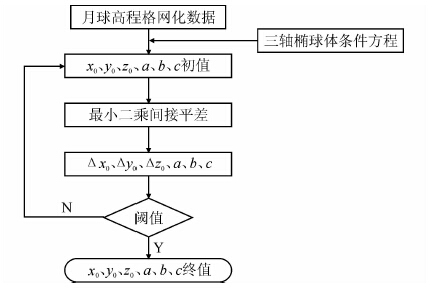 |
| 图 2 月球三轴几何椭球体的拟合流程图 Figure 2 The Flow Diagram of Fitting Lunar Tri-axial Geometrical Ellipsoid |
2 三轴水准椭球体模型的建立
月球表面及其外部空间一点的重力位为[3]:
| $\eqalign{ & W = {{GM} \over \rho }1 + \cr & \left\{ {\sum\limits_{n = 2}^\infty {{{\left( {{{{a_0}} \over \rho }} \right)}^n}\sum\limits_{m = 0}^n {\left( {{C_{nm}}\cos m\lambda + {S_{mn}}\sin m\lambda } \right) \bullet {P_{nm}}\left( {\sin \varphi } \right) + {1 \over 6}\left( {{{{a_0}} \over \rho }} \right)} } } \right. \cr & q\left[ {2 - 5{P_2}\left( {\sin \varphi } \right) + {3 \over 2}{P_{22}}\left( {\sin \varphi } \right)\cos 2\lambda } \right] \cr} $ | (8) |
式中,GM为月球引力常数;a0为月球参考半径;ρ、φ、λ分别为月心球坐标系的向径和经纬度;Cnm、Snm为月球引力位球谐系数;Pnm为n阶m次连带勒让德函数;q为形状参数。
月球大地水准面的球谐展开式可表示为[6]:
| ${{\rho }_{S}}={{R}_{0}}\left[ \sum\limits_{l=0}^{N}{\sum\limits_{m=0}^{l}{{{P}_{lm}}(sin\varphi )\left( {{C}_{lm}}\cos m\lambda +{{S}_{lm}}\sin m\lambda \right)}} \right]$ | (9) |
式中,ρS为大地水准面上各点在参考坐标系中的向径;R0为球谐展开式的尺度函数。
月球大地水准面尽量与物理表面贴近,其尺度因子与平均半径的关系为R0=t1-13ω23tGM,t是月球平均半径。相应的大地水准面重力位为常数,即W0=GMR0。
使用Stokes方法,取最逼近大地水准面的三轴椭球作为正常椭球,用半轴长a、赤道扁率α、极扁率α1以及子午面指向Λa4个参数表示正常椭球向径:
| ${{\rho }_{e}}=\left( a,\alpha ,{{\alpha }_{1}},{{\Lambda }_{a}} \right)$ | (10) |
将ρe代入重力位式(8) ,得到椭球面上重力位WE。令WE=W0,q=ω02a3GM(ω为月球自转角速度),建立包含4个椭球参数的限制方程,略去10-9量级及更小的项,求解得:
| $\eqalign{ & a = {R_0}\left\{ {1 - {1 \over 2}{{\left( {{{{a_0}} \over {{R_0}}}} \right)}^2}\left( {{C_{20}} - 6C_{22}^*} \right) + } \right.{\left( {{{{a_0}} \over {{R_0}}}} \right)^4} \cr & {\left[ {{7 \over {40}}C_{20}^2 - {3 \over 2}{C_{20}}C_{22}^* + {{1033} \over {70}}C_{22}^*} \right]^2} + {R_0} \cr & \left\{ {{{\left( {{{{a_0}} \over {{R_0}}}} \right)}^{ - 1}}q\left( {{{13} \over {14}}{C_{20}} + {{457} \over {35}}C_{22}^*} \right) + {3 \over 2}{{\left( {{{{a_0}} \over {{R_0}}}} \right)}^{ - 3}}q} \right. + \cr & {{461} \over {140}}{\left( {{{{a_0}} \over {{R_0}}}} \right)^{ - 6}}\left. {{q^2}} \right\} \cr} $ | (11) |
| $\eqalign{ & a = - {3 \over 2}{\left( {{{{a_0}} \over {{R_0}}}} \right)^2}\left( {{C_{20}} - 2C_{22}^*} \right) + {\left( {{{{a_0}} \over {{R_0}}}} \right)^4} \bullet \cr & {\left[ { - {3 \over 8}C_{20}^2 + {9 \over 2}{C_{20}}c_{22}^* + {{15} \over {14}}C_{22}^*} \right]^2} + {3 \over {14}}{\left( {{{{a_0}} \over {{R_0}}}} \right)^{ - 1}} \bullet \cr & q\left( {{{23} \over 2}{C_{20}} + C_{22}^*} \right) + 2{\left( {{{{a_0}} \over {{R_0}}}} \right)^{ - 3}}q - {1 \over {28}}{\left( {{{{a_0}} \over {{R_0}}}} \right)^{ - 6}}{q^2} \cr} $ | (12) |
| $\eqalign{ & {\alpha _1} = 6{\left( {{{{a_0}} \over {{R_0}}}} \right)^2}C_{22}^* + {3 \over 2}{\left( {{{{a_0}} \over {{R_0}}}} \right)^{ - 3}}q + {\left( {{{{a_0}} \over {{R_0}}}} \right)^4} \cr & C_{22}^*\left[ {{{15} \over 7}{{\left( {{{{a_0}} \over {{R_0}}}} \right)}^{ - 5}}q - {{66} \over 7}C_{22}^*} \right] + {9 \over 8}{\left( {{{{a_0}} \over {{R_0}}}} \right)^{ - 6}}{q^2} \cr} $ | (13) |
| $\tan 2{{\Lambda }_{a}}=\frac{{{S}_{22}}}{{{C}_{22}}},C_{22}^{*}={{\left( C_{22}^{2}+S_{22}^{2} \right)}^{{1}/{2}\;}}$ | (14) |
本文选取LRO分辨率为0.062 5°的全月球高程模型数据建立最佳符合地形的全月球三轴几何椭球体模型,从而计算出月球的基本形状参数,如半径和质心形心偏移量。结果如表 1所示。
| 表 1 本文LRO数据拟合得到的三轴几何椭球体参数 Table 1 Parameters of Lunar Tri-axial Geometrical Ellipsoid with LRO Data |
 |
可见,本文LRO_LTM02测高模型拟合月球三轴几何椭球体,三条半轴长分别为1 737.902 3、1 737.659 8和1 735.987 7 km;三轴几何椭球体的中心可作为月球形心,在质心坐标系中的坐标为(-1.527 5,-0.693 2,0.230 5) km,该偏差沿月球旋转轴方向以北0.230 5 km,沿月固坐标系x和y方向分别为-1.527 5 km和-0.693 2 km。
表 2分别列出了使用本文LRO_LTM02测高模型、嫦娥一号LAM数据[1]、SELENE359阶次模型STM359_grid-02[7]以及嫦娥一号360阶次月球全球地形球谐模型CLTM-s01[8]计算的月球三条主轴长和质心形心偏移量。表 2中,平均赤道半径为三轴几何椭球体在赤道面上的两条半长轴a、b的平均值,极半径为三轴几何椭球体在极平面上的半长轴c,平均半径为三条半长轴的平均值。
| 表 2 利用最小二乘法求解得到的三轴几何椭球体参数 Table 2 Parameters of Lunar Tri-axial Geometrical Ellipsoid Using Least Squares Method |
 |
本文LRO_LTM02测高模型与嫦娥一号LAM数据使用最小二乘法拟合月球三轴几何椭球体,Araki与平劲松使用位系数法计算月球几何椭球体。本文使用最小二乘法有一定的优势,能够更加全面地拟合最佳符合地形,求得的结果更客观。
与CLTM-s01计算结果比较,STM359_grid-02模型计算结果的平均赤道半径偏大994 m,极半径偏小183 m,平均半径偏大137 m。
由表 2可见,嫦娥一号LAM数据求得的月球形状中心和质量中心在月球三轴几何椭球基准下的偏差为(-1.530 0,-0.694 0,0.227 0) km,主要沿地月连线方向,该偏差沿月球旋转轴方向以北为0.227 0 km;沿月固坐标系的x和y方向分别为-1.530 0 km和-0.694 0 km。 与表 1中数据对比可知,本文使用的LRO_LTM02测高模型的精度和分辨率要优于嫦娥一号LAM数据,因此解算的结果更可靠。
3.2 三轴水准椭球体本文使用Goddard解算的GRAIL卫星660阶次重力场球谐模型GRGM660PRIM[9],联合LRO地形模型,拟合了月球三轴水准椭球体。结果如表 3所示。
| 表 3 三轴水准椭球体拟合结果 Table 3 Fitting Results of Lunar Tri-axial Level Ellipsoid |
 |
表 3分别给出了本文GRGM660PRIM模型与LP150Q[1]、IERS1989[10]以及IERS1992[11]拟合三轴水准椭球体的计算结果。利用IERS standards提供的4阶次月球重力位模型IERS1989以及IERS1992解算月球三轴水准椭球体参数,但是采用的重力场模型不同。其中S22=0,则长半轴指向与月心坐标系X轴重合(Λa=0) 。IERS standards模型重力位系数阶次过低,且精度有限。因此,利用较新的月球重力场模型进行解算和分析是有必要的。
GRGM660PRIM模型以及IERS1989解算月球大地水准面时,顾及了地球引潮力的影响,并且以椭球体表面为等位面作为限制条件,所以得到的椭球体形状(即极扁率和赤道扁率)近似。但是半轴长计算结果差异明显,最大相差412 m;月球地形模型不同,平均半径不同,导致W0和R0不同,进而椭球长半轴值不同。GRGM660PRIM模型的R0值取地形球谐模型的平均向径;而IERS1989先计算W0,进而得到R0值。
LP150Q以及IERS1992没有考虑地球引潮力的影响,以求最佳拟合椭球为目标,椭球表面不一定满足等位要求。月球参考半径a0值的大小也影响解算结果。改变a0的值,对结果影响比较大,特别是对扁率的影响。本文计算中,a0值采用重力模型的参考半径值。
4 结束语通过本文的计算分析,可以得到如下三点结论:
1) 本文使用LRO激光测高数据拟合的月球三轴几何椭球体,平均赤道半径为1 737.781 0 km,极半径为1 735.987 7 km,平均半径为1 737.183 3 km。月球形心在质心坐标系中的坐标为(-1.527 5,-0.693 2,0.230 5) km,偏移总量为1.693 2 km,与文献[1]使用嫦娥一号LAM数据解算的结果大小和量级相差不大,但高分辨LRO地形模型提供了更全面的月球背面数据,解算结果更加可靠。
2) 联合GRAIL重力场模型(gggrx_0660pm_sha)和LRO激光高度计地形数据,拟合出月球三轴水准椭球体,其三条半径分别为1 737.460 9 km、1 737.207 6 km和1 736.787 7 km,赤道扁率为1/2 581,极扁率为1/6 860。本文顾及了地球引潮力的影响,并且使用最新高分辨高精度GRAIL重力场模型,解算结果更加可靠,与LP150Q模型解算结果比较可知:赤道扁率偏小,极扁率偏大。
3) 比较本文解算的三轴几何椭球体和三轴水准椭球体:半轴长a、b、c分别相差0.441 4、0.452 2和-0.8 km,而且中心不重合。因此,三轴几何椭球和三轴水准椭球并不平行。尽管二者的半轴长差值不大,但用三轴几何椭球体表面代替三轴水准椭球是不严谨的。
| [1] |
王文睿, 李斐, 刘建军, 等. 基于嫦娥一号激光测高数据的月球三轴椭球体模型[J].
中国科学:地球科学,2010,40(8) : 1022–1030.
Wang Wenrui, Li Fei, Liu Jianjun, et al. Triaxial Ellipsoid Models of the Moon Based on the Laser Altimetry Data of Chang'E-1[J]. Science China: Earth Sciences,2010,40(8) : 1022–1030. |
| [2] | Pererav, Garrick-Bethell I. Lunar Asymmetry:Coincidence of the Degree-1 and Degree-2 Features Due to a Rayleigh-Taylor Instability and Reorientation[C].The 42nd Lunar and Planetary Science Conference,The Woodlands,Texas,2011 |
| [3] |
丰海, 李建成, 李大炜, 等. 新的月球大地水准面模型与参考三轴水准椭球[J].
大地测量与地球动力学,2013,33(4) : 133–136.
Feng Hai, Li Jiancheng, Li Dawei, et al. A New Selenoid Model and Reference Triaxial Level Ellipsoid[J]. Journal of Geodesy and Geodynamics,2013,33(4) : 133–136. |
| [4] |
鄢建国, 平劲松, KOJIMatsumoto, 等. 嫦娥一号绕月卫星对月球重力场模型的优化[J].
中国科学:物理学、力学、天文学,2011,41(7) : 870–878.
Yan Jianguo, Ping Jingsong, KOJI Matsumoto, et al. Optimization on Lunar Gravity Field Model Using Chang'E-1 Orbital Tracking Data[J]. Science China: Phys, Mech&Astron,2011,41(7) : 870–878. |
| [5] | Gao Buxi. An Estimate on the Lunar Figure[J]. Chinese Astronomy and Astrophysics,2009,33(2) : 179–187. DOI:10.1016/j.chinastron.2009.03.010 |
| [6] | Bursa M. Dimension Parameters of the Moon, Mars and Venus[J]. Bull Astron Inst Czechosl,1989,40 : 284–288. |
| [7] |
平劲松, 黄倩, 鄢建国, 等. 基于嫦娥一号卫星激光测高观测的月球地形模型CLTM-s01[J].
中国科学:物理学、力学、天文学,2008,38(11) : 1601–1612.
Ping Jinsong, Huang Qian, Yan Jianguo, et al. Lunar Topographic Model CLTM-s01 from Chang'E-1 Laser Altimeter[J]. Science China: Phys, Mech&Astron,2008,38(11) : 1601–1612. |
| [8] | Araki H,Tazawa S, Noda H, et al. The Lunar Global Topography by the Laser Altimeter(LALT) on Board Kaguya (SELENE):Results from the One Year observation[C].The 40th Lunar and Planetary Science Conference, The Woodlands, Texas, 2009 |
| [9] | Lemoine F G, Goossens S, Sabaka T J, et al. High-degree Gravity Models from GRAIL Primary Mission Data[J]. Journal of Geophysical Research Planets,2013,118(8) : 1676–1698. DOI:10.1002/jgre.v118.8 |
| [10] | Bursa M. Distortions of the Moon's Figure Due to the Earth[J]. Earth,Moon and Planets,1994,64 : 265–271. DOI:10.1007/BF00572152 |
| [11] |
张承志. 月球的力学形状以及月球物理参数的研究[J].
南京大学学报(自然科学版),1993,29(4) : 569–580.
Zhang Chengzhi. Research on the Mechanical Shape and the Physical Parameters of the Moon[J]. Journal of Nanjing University(Natural Sciences Edition),1993,29(4) : 569–580. |
 2016, Vol. 41
2016, Vol. 41

