精密单点定位(precise point positioning，PPP)技术最初因其在大规模数据解算中的高效率而被提出^[1]。不同于差分定位，PPP无需基准站网支持，作业方式灵活简单，可在全球范围内提供瞬时cm级精度定位服务，极大地降低了作业成本^{[2, 3]}。PPP技术也有自身的瓶颈，即较长的收敛时间和浮点模糊度解^[4]。PPP收敛时间一般需要15 min甚至更久，这极大地限制了其在实时领域的应用^[5]。PPP模糊度固定(ambiguity resolution，AR)能够显著改善定位精度，尤其是在东方向^{[6, 7]}；此外AR也能够加速PPP收敛速度，提高作业效率^[8]。本文的研究主要围绕如何快速有效地固定非差模糊度展开。

已有研究证明用于模糊度固定的备选模糊度越多，部分模糊度固定策略的成功率越高^[7-9]。GNSS多系统PPP-AR因更多的备选模糊度参与模糊度固定将会显著缩短PPP首次模糊度固定所需的时间。Liu等通过联合GPS/GLONASS/BeiDou 3个系统进行了PPP-AR试验，对于单GPS的PPP-AR仅有16.2%的解在10 min内实现模糊度固定；如果加入GLONASS和BeiDou数据并参与模糊度固定，这一比例提高为90.0%^[10]。然而以上多系统PPP-AR的研究中关于GLONASS模糊度固定部分假设同类接收机的IFCBs(inter frequency code Bias)影响一致，从而在进行FCBs(fractional cycle Bias)估计及单站PPP-AR时忽略了IFCBs的影响。有关IFCBs的研究表明，这一假设并不严密^{[11, 12]}。本文通过试验也评估了GPS/GLONASS/BeiDou/Galileo 4系统PPP-AR对首次模糊度固定时间的影响。关于GLONASS模糊度固定部分，本文选择由Yi等提出的窄巷模糊度固定法^[13]，其无需考虑接收机类型，具有更广的应用范围。

BeiDou目前仅面向亚太区域提供服务，试验数据选取2017年第225~255天能同时跟踪GPS/GLONASS/BeiDou/Galileo的澳大利亚观测网数据如图 1所示，共包含20个测站。实心圆为参考站，总共5个，用于估计卫星钟差、宽巷和窄巷FCBs等信息；空心圆为流动站，共15个，用于进行动态滤波PPP-AR测试。

图 1(Figure 1)

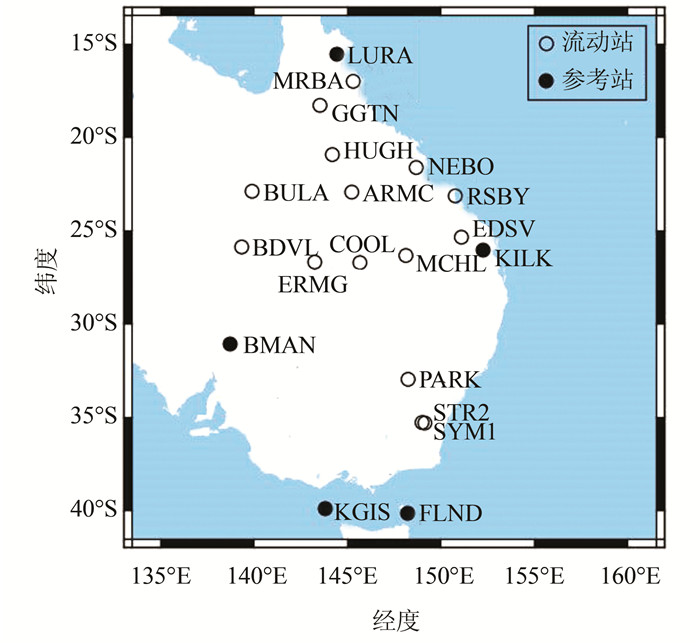图 1 测站分布图 Figure 1 Station Distribution Map

CODE(Center for Orbit Determination in Europe)的轨道和ERP产品在数据处理中作为已知量使用。卫星钟差通过均方根信息滤波器根据历元间差分方法估计^[14]。数据处理中考虑了码偏差(比如P1-C1)的影响，并且BeiDou根据Wanninger等^[15]提出的多路径改正模型消除了卫星端码观测值多路径效应。ZTD(zenith troposphere delay)参数时间更新频率为2 h，映射函数为GMF(Global Map Function)，相邻ZTD参数的随机游走过程噪声为$2\;{\rm{cm/}}\sqrt {\rm{h}} $。接收机钟差作为白噪声参数进行估计。接收机端和卫星端PCO(phase center offset)及PCV(phase center variation)、相位缠绕、固体潮、海潮及极移潮等误差项均进行了精确的模型化改正。相位观测值精度设为2 cm，伪距精度为2 m。可用观测值截止高度角为7°，可用于FCBs计算及模糊度固定的模糊度截止高度角为10°。对于PPP-AR，位置参数在历元间不施加强约束。宽巷FCBs以天为更新频率；窄巷FCBs更新频率为15 min，相邻历元的FCBs间不施加任何约束。

15个用于测试PPP-AR的测站观测数据被划分成1 h长度的观测弧段，总共包含11 160个PPP-AR测试解。第一个小时的数据处于卫星钟差和FCBs的滤波收敛阶段，因此不参与PPP-AR测试。宽巷模糊度估值由Melbourne-Wübbena组合^[16]得到，由Rounding方法确定为整数^[17]。窄巷整数模糊度由LAMBDA(least squares ambiguity decorelation adjustment)方法^[18]搜索得到，通过Ratio检验加以确认，限值设为3。对于窄巷模糊度，若不能全部固定备选模糊度则采用部分固定策略。至少有5个及以上非差窄巷模糊度固定则认为该历元为模糊度固定解。通过Ratio检验的固定解并不等同于正确固定解，实际上当备选模糊度估值精度不高时，错误固定的情况时常发生，因此为了避免这种错误情况造成严重后果，试验中每个历元重新进行PPP-AR而不是将已经固定的模糊度直接施加强约束。本试验中定义首次模糊度固定时间为首次固定历元之后的所有历元均固定，并且固定后相比于天解测站坐标的定位误差在平面不超过4 cm，高程方向不超过10 cm。

GPS/GLONASS/BeiDou/Galileo均参与PPP浮点解的计算，不同的仅是模糊度固定部分，依此来评价多系统PPP-AR在定位上的表现。共7种不同系统组合方式进行模糊度固定试验，方案如下：①GPS固定；②GPS/GLONASS固定；③GPS/BeiDou固定；④GPS/Galileo固定；⑤GPS/GLONASS/BeiDou固定；⑥GPS/GLONASS/Galileo固定；⑦GPS/GLONASS/BeiDou/Galileo固定。

事后模式的平滑解相比于滤波解具有更高的精度, 可用于测试算法所能达到的极限性能, 因此先用平滑解模糊度估值来验证算法的效能。

图 2为2017年第225~255天宽巷时间序列及整个观测周期所有测站移除FCBs后单差宽巷模糊度小数部分分布情况，图中每个系统分别选择了5颗示例卫星。图 2(a)中，GPS的宽巷FCBs时间序列表现出了很好的时间稳定性，最大标准差为0.03周；移除FCBs后单差宽巷模糊度残余小数部分98.8%落在了±0.15周内，残余小数部分的标准差为0.05周。从图 2(b)可知，GLONASS的宽巷时间序列相比于GPS波动较大，最小标准差为0.03周，与GPS的最大标准差接近，但是其相邻两天的宽巷FCBs值并无大的跳变；移除FCBs后单差宽巷模糊度残余小数部分99.2%落在了±0.15周内。这一比例高于GPS，因为在GLONASS数据处理时，对影响FCBs及宽巷模糊度固定的频间宽巷偏差进行了逐测站逐卫星的校正，而频间宽巷偏差在消除IFCBs影响的同时也势必会消除一些未知的测站卫星共性误差，因此使得GLONASS宽巷模糊度具有更好的整数特性。图 2(c)中，Galileo的宽巷FCBs时间序列相比于其他系统表现最不稳定，尤其是E14和E26两颗卫星发生明显抖动；移除FCBs后单差宽巷模糊度残余小数部分96.7%落在了±0.15周内，略低于GPS 2.1%。从图 2(d)中可知，IGSO卫星的时间序列相比于MEO卫星的时间序列要更加平滑，因为IGSO卫星具有更长的可视时间，而较长的观测意味着更为精确的宽巷模糊度估值；移除FCBs后的单差宽巷模糊度残余小数部分89.6%落在了±0.15周内，这一比例低于其他3个系统，大约比GPS低了9.2%，这应该是因为BeiDou卫星端码观测值的多路径影响并未完全消除造成的。

图 2(Figure 2)

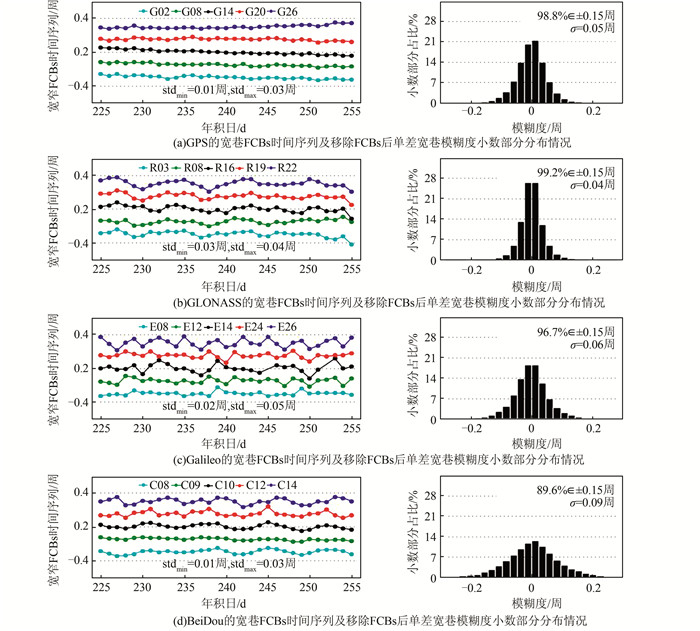图 2 2017年第225~255天宽巷FCBs时间序列及移除FCBs后单差宽巷模糊度小数部分分布 Figure 2 Wide-Lane FCBs Time Series on the 225-255 Day in 2017 and Distribution of Wide-Lane Fractional Parts After Removal of FCBs

一旦得到了宽巷FCBs之后，即可计算窄巷FCBs。图 3为2017年第225天事后模式估计的窄巷FCBs时间序列及连续31天所有测站移除FCBs后单差窄巷模糊度残余小数部分的分布情况。图 3中分别展示了每个系统5颗示例卫星的FCBs时间序列，可以看出，4个系统的FCBs随时间均表现出了较好的稳定性，一次完整的卫星跟踪弧段仅用常量即可准确描述。从图 3中也可清晰看到，对于一颗卫星的不同弧段，其FCBs值存在明显的差异；经FCBs改正后，单差窄巷模糊度的残余小数部分约98%落在了(-0.15, 0.15)周范围内，对应标准差约为0.05周，证明了4个系统经窄巷FCBs修正后，模糊度均具有较好的整数特性。其中BeiDou的残余小数部分约98.9%落在了±0.15周内，这在4个系统中最高，这是因为窄巷模糊度残余小数部分的提取是在宽巷固定的前提下进行的，而BeiDou宽巷固定比例为89.6%，在4个系统中最低，因此筛选掉了部分问题模糊度使得用于窄巷固定的模糊度具有较好的估值精度。

图 3(Figure 3)

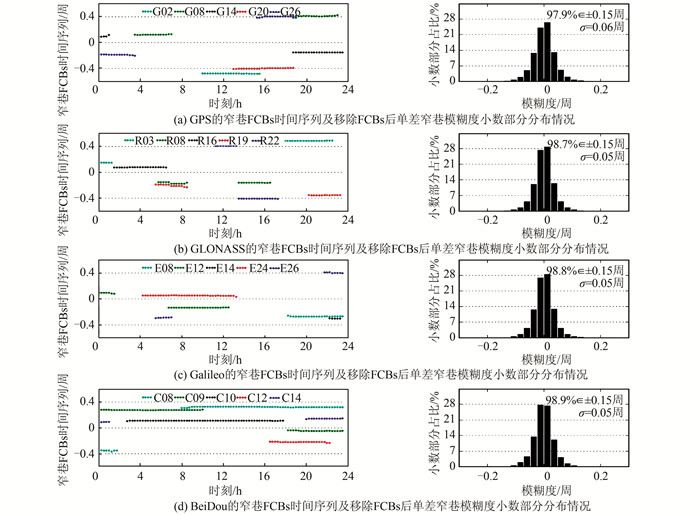图 3 2017年第225天事后模式估计的窄巷FCBs时间序列及第225~255天所有测站移除FCBs后单差窄巷模糊度残余小数部分分布情况 Figure 3 Narrow-Lane FCBs Time Series on the 225 Day in 2017 and Distribution of Narrow-Lane Fractional Parts After Removal of FCBs

求得了事后模式的宽巷和窄巷FCBs之后，即可进行单站的PPP-AR试验。此外，对于GLONASS系统，还需频间宽巷偏差和频间窄巷偏差信息辅助。对观测网所有测站2017年第225~255天的数据进行了事后PPP-AR，统计每个测站宽巷、窄巷及顾及无FCBs可用情况的模糊度固定百分比。对于宽巷部分，GPS的模糊度固定比例为99.7%，Galileo则为98.4%；对于BeiDou系统，ARMC和BULA的固定比例约为80%，其他站的比例均超过90%，总体平均值为96.2%，略低于GPS 3.5%。GLONASS模糊度固定比例可达99.6%，通过频间宽巷偏差的校正，有效地解决了GLONASS IFCBs对宽巷模糊度固定的影响。关于窄巷部分，GPS窄巷固定比例的总体平均值为96.5%，Galileo为96.1%，BeiDou为94.2%，而GLONASS则为90.6%，为4个系统中最低。需要指出的是，个别模糊度未固定是因为缺少对应卫星的FCBs产品。如果窄巷模糊度固定比例加上因没有FCBs产品而未固定的比例，此时4个系统的比例均为98.9%，表明在窄巷模糊度固定上4个系统的表现相当。这也证明了在GLONASS系统中频间窄巷偏差很好地消除了频间宽巷偏差隐含整数的影响。总的来说，4个系统的模糊度均具有较好的整数特性，为动态滤波模式评价多系统PPP-AR对首次模糊度固定时间的影响奠定了基础。

考虑到动态滤波PPP的广泛应用，首次模糊度固定时间作为动态滤波PPP的核心指标是我们关心的重要问题。本节评价了4个系统PPP模糊度固定在动态滤波情况下对首次模糊度固定时间的影响。

图 4是2017年第225天测站COOL的GPS/GLONASS/BeiDou/Galileo动态滤波PPP小时解定位误差时序图，其中红色是GPS/GLONASS/BeiDou/Galileo固定的固定解，绿色是浮点解。第1个小时用于卫星钟差和FCBs估计的收敛阶段，不参与PPP-AR，之后的每个小时重新初始化。该站在2017年第225天的平均首次模糊度固定时间为100 s，而如果仅固定GPS卫星的模糊度，则平均首次模糊度固定时间为330 s，多系统PPP-AR显著缩短了首次模糊度固定时间，对于第225天的COOL站，其收敛时间缩短了近70%。关于定位精度，COOL的固定解相比浮点解改善明显，浮点解在东、北及高程3个方向的定位误差RMS分别为6.4 cm、2.7 cm及6.5 cm，东方向误差为北方向的两倍多，基本同高程方向一致；而经模糊度固定后，东、北及高程3个方向的定位误差RMS分别减小为0.9 cm、0.6 cm及2.0 cm，东方向的定位误差RMS同北方向基本一致，并且仅为高程方向的1/2。表 1进一步统计了2017年第225~255天连续31天流动站动态滤波PPP的小时解定位误差RMS。7种固定模式的平面误差RMS均优于2 cm，高程方向均优于3 cm。对于浮点解，东方向的定位误差RMS明显大于北方向，但模糊度固定后，东方向和北方向的大小接近。GPS固定模式的浮点解定位误差RMS优于其他固定模式，这是因为多系统模糊度固定模式的首次模糊度固定时间更短，因此，其参与定位误差RMS统计的时段包含了更多初始化阶段，从而导致浮点解的统计结果更差。

图 4(Figure 4)

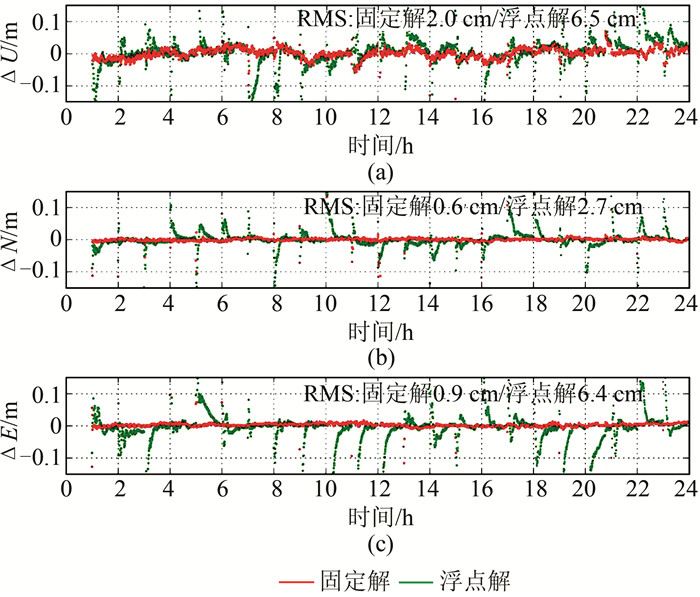图 4 2017年第225天测站COOL的GPS/GLONASS/BeiDou/Galileo PPP小时解定位误差时序图 Figure 4 Time Series of PPP Errors for COOL on the 225 Day in 2017

表 1(Table 1)

表 1 2017年第225~255天流动站的GPS/GLONASS/BeiDou/Galileo PPP小时解定位误差RMS /cm Table 1 RMS of PPP Errors for Rover Stations over 31 Days/cm

表 1 2017年第225~255天流动站的GPS/GLONASS/BeiDou/Galileo PPP小时解定位误差RMS /cm Table 1 RMS of PPP Errors for Rover Stations over 31 Days/cm 固定模式 东 北 高 GPS固定 1.0/4.1 0.6/1.5 2.3/3.9 GPS/GLONASS固定 1.6/5.8 0.9/2.4 2.8/5.4 GPS/BeiDou固定 1.5/5.7 0.8/2.3 2.6/5.3 GPS/Galileo固定 1.5/5.5 0.9/2.3 2.7/5.2 GPS/GLONASS/BeiDou固定 1.4/6.7 0.9/2.9 2.7/6.4 GPS/GLONASS/Galileo固定 1.5/6.6 0.9/2.9 2.7/6.4 GPS/GLONASS/BeiDou/Galileo固定 1.3/7.3 0.9/3.3 2.6/7.2

图 5为2017年第225~255天所有测站动态滤波小时解的首次模糊度固定时间分布，共包含7种固定模式。图 5(a)为GPS固定模式的首次模糊度固定时间分布，在1 h PPP解中有99.5%的固定解。对于双系统固定，比如GPS/GLONASS固定、GPS/BeiDou固定及GPS/Galileo固定，在1 h PPP解中有99.6%的固定解，相比单系统基本没有变化，但是双系统PPP-AR的时间分布更多地积聚在了时间轴的左侧，意味着在较短的时间内有更高的固定解比例。当为3个系统固定时，比如GPS/GLONASS/BeiDou固定和GPS/GLONASS/Galileo固定，在1 h PPP解中有99.7%的固定解，相比单系统基本一致，但是3系统PPP-AR的时间分布相比于单系统和双系统在时间轴左侧的积聚性表现得更为明显。如果进一步全部固定GPS/GLONASS/BeiDou/Galileo 4系统的模糊度，首次模糊度固定时间的分布在时间轴的左侧最为积聚，表明4系统PPP-AR在较短的时间内固定解的比例最高。

图 5(Figure 5)

图 5 2017年第225~255天所有测站动态滤波小时解的首次模糊度固定时间分布 Figure 5 Distribution of Time of First AR for Rover Stations over 31 Days

多系统PPP-AR可增加用于模糊度固定的备选模糊度个数，显著改善部分模糊度固定策略的成功率，从而缩短首次模糊度固定时间。图 6(a)给出了动态滤波PPP小时解的每天流动站首次模糊度固定时间。GPS固定模式的首次模糊度固定时间为533 s，是7种固定模式中费时最长的。若在GPS固定基础上再增加一个系统，即GPS/GLONASS、GPS/BeiDou及GPS/Galileo，首次模糊度固定时间会显著缩短为320 s左右，相比单系统时大约缩短了40%。而在双系统组合中，GPS/GLONASS的首次模糊度固定时间最短，为313 s；GPS/Galileo的首次固定时间最长，为339 s。在两个系统的基础上进一步增加一个系统，即GPS/GLONASS/BeiDou固定和GPS/GLONASS/Galileo固定，则首次模糊度固定时间进一步减小为225 s左右，相比于单系统降低了近58%，而相比于双系统则降低了30%。如果将目前全部可用的导航卫星用于PPP-AR，即GPS/GLONASS/BeiDou/Galileo固定，则首次模糊度固定时间仅为176 s，是7种固定模式中时间最短的；相比于GPS固定模式费时降低了67%，显著缩短了模糊度固定所需的时间。根据每天统计结果曲线可以看到，上述改进在整个31 d的观测期间稳定存在。双系统的曲线基本重叠且在单系统曲线的下方，3系统曲线又在双系统曲线的下方且重叠在一起，最下方是4系统的首次模糊度固定曲线，可以看到7种固定模式的曲线分为4组，并能层次清晰地显示，表明了多系统PPP-AR在提高模糊度固定效率方面的重要贡献。

图 6(Figure 6)

图 6 2017年第225~255天流动站的首次模糊度固定时间及300 s、600 s、1 200 s内固定解百分比 Figure 6 Time of First AR and the Percentage of the Time of First AR Within 300 s, 600 s and 1 200 s for Rover Stations over the 31 Days

图 6(b)~6(d)为每天流动站动态滤波PPP小时解首次模糊度固定时间分别小于300 s、600 s及1 200 s的固定解百分比。当首次模糊度固定时间小于300 s时，GPS固定模式有28%的固定解。若由单系统增加为双系统固定时，这一比例提高为65%左右，相比单系统提高了37%。当3系统固定时，则固定解的比例达到约85%。如果使用全部4个系统参与固定时，固定解的比例进一步提高为90%，相比于单系统提高62%。当首次模糊度固定时间小于600 s时，GPS固定模式的固定解比例为72%，固定解比例随着观测时间的变长显著提高，相比首次模糊度固定时间小于300 s时提高了44%；双系统固定模式的固定解比例则由300 s时的65%提高为90%；3系统和4系统固定模式的固定解比例比较接近，约95%。当观测时间延长为1 200 s时，7种解算模式的固定解比例基本一致，为97%，单系统也均能实现模糊度固定解。这一结果证明了多系统PPP-AR对PPP快速模糊度固定至关重要；4系统均参与固定的情况下，5 min内的固定解比例可高达90%，相比单系统提高了62%。

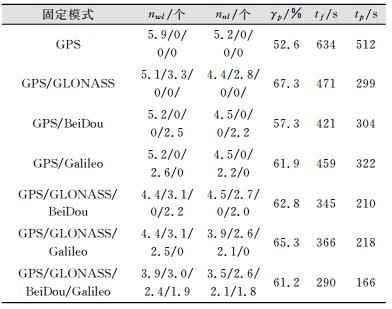
当有更多备选模糊度参与模糊度固定时，部分模糊度固定策略会缩短首次模糊度固定时间。表 2给出了不同固定模式下部分AR的统计结果，包括用于固定的备选模糊度个数(n_wl)、固定模糊度个数(n_nl)、部分模糊度固定解百分比γ_p、首次全部模糊度固定时间t_f及首次部分模糊度固定时间t_p。对于GPS固定模式，用于窄巷模糊度固定的备选模糊度为5.9个，部分模糊度固定解的百分比为52.6%。对于GPS/GLONASS固定模式，用于窄巷固定的备选模糊度个数为8.4，其中由于各系统选择各自的参考星，有效个数为7.4个，部分模糊度固定解的比例则为67.3%。而对于GPS/BeiDou固定和GPS/Galileo固定模式，实际有效的备选模糊度个数则为6.7个，部分模糊度固定解的比例为60%左右。对于GPS/GLONASS/BeiDou/Galileo固定模式，备选模糊度有效个数为8.2个，部分模糊度固定解的比例为61.2%。备选模糊度个数并未随着系统的增加显著增加，这是因为随着系统增加，首次模糊度固定时间也在缩短，比如4系统固定的首次模糊度固定时间不超过3 min，此时大多数模糊度估值的精度还不足以作为备选模糊度。从另一角度来看，如果不是4系统PPP-AR，则在初始化3 min时刻处用于模糊度固定的备选模糊度将远少于8个，因此多系统PPP-AR显著增加了备选模糊度个数。7种固定模式的部分模糊度固定解比例均超过了50%，表明部分模糊度固定策略在PPP-AR中起着关键作用。部分模糊度固定策略显著缩短了PPP首次模糊度固定时间，以4系统模糊度固定为例，部分固定策略下的首次模糊度固定时间为166 s，若不采用部分固定策略时则为290 s，证明了部分模糊度固定策略显著缩短了多系统PPP-AR的首次模糊度固定时间。

表 2(Table 2)

表 2 不同固定模式下部分AR的统计结果 Table 2 Statistics on Partial AR for Difference Solution Types

表 2 不同固定模式下部分AR的统计结果 Table 2 Statistics on Partial AR for Difference Solution Types 固定模式 nwl/个 nnl/个 γp/% tf/s tp/s GPS 5.9/0/0/0 5.2/0/0/0 52.6 634 512 GPS/GLONASS 5.1/3.3/0/0/ 4.4/2.8/0/0/ 67.3 471 299 GPS/BeiDou 5.2/0/0/2.5 4.5/0/0/2.2 57.3 421 304 GPS/Galileo 5.2/0/2.6/0 4.5/0/2.2/0 61.9 459 322 GPS/GLONASS/BeiDou 4.4/3.1/0/2.2 4.5/2.7/0/2.0 62.8 345 210 GPS/GLONASS/Galileo 4.4/3.1/2.5/0 3.9/2.6/2.1/0 65.3 366 218 GPS/GLONASS/BeiDou/Galileo 3.9/3.0/2.4/1.9 3.5/2.6/2.1/1.8 61.2 290 166

本文评估了GPS/GLONASS/BeiDou/Galileo 4系统PPP-AR对首次模糊度固定时间的影响，需要指出的是，关于GLONASS模糊度固定部分使用的GLONASS窄巷模糊度固定方法无需考虑接收机类型，具有更广的应用范围。当首次模糊度固定时间小于300 s时，GPS固定模式的固定解比例仅为28%，若改为GPS/GLONASS/BeiDou/Galileo固定模式，则固定解比例可高达90%，通过多系统PPP-AR，使得固定解的比例提升了68%。GPS固定模式的首次模糊度固定时间为533 s，若改为GPS/GLONASS/BeiDou/Galileo固定模式，则仅为176 s，相比于单GPS模糊度固定缩短357 s，改进了约67%。部分模糊度固定策略可显著缩短多系统PPP-AR的首次模糊度固定时间。对于GPS/GLONASS/BeiDou/Galileo固定模式，全部模糊度固定解的首次模糊度固定时间为290 s，部分模糊度固定策略使得首次模糊度固定时间大约缩短了43%，降为166 s。