| 基于固定点初始化的室内伪卫星定位方法研究 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China
全球卫星导航系统 (global navigation satellite system, GNSS) 在室外信号无遮挡的情况下具有全天候、精度高、可靠性强等优点[1],但在室内环境下却无法满足定位功能,为了实现室内如大型工厂车间精密定位,室内伪卫星系统应运而生,可以在一定程度上弥补GNSS室内无法高精度定位的致命缺陷[2]。传统的伪卫星系统中,要求所有伪卫星时钟需要严格同步,如Locata系统[3]和i-Going系统[4]中的伪卫星都采用了非常严格的时钟同步机制来确保伪卫星之间的时钟同步,这给系统部署带来了很大的开销。而且在室内环境中,多路径效应显著,伪距相对精度较差,载波观测值也频繁中断[5, 6],理论上无法通过单历元求解模糊度,另外伪卫星系统由于卫星星座固定不变导致几何强度不高[7],线性化误差较大[8, 9],这些都给伪卫星模糊度求解带来了较大的挑战。
本文采用GNSS领域中的双差模式,有效地消除了伪卫星和接收机钟不同步造成的误差,模型大大简化,利用固定点静态初始化,模糊度固定采用LAMBDA算法,在接收机载体开始移动时,采用迭代卡尔曼滤波 (extend Kalman filtering,EKF)[10]有效地削弱伪卫星线性化误差,并根据载体的概略移动速度,对需要实时求解的接收机坐标进行相应的松弛约束,实现了室内优于5 mm的高精度实时动态定位。
1 基于固定点初始化的室内伪卫星定位方法 1.1 双差模型接收机 (r) 和伪卫星 (s) 对应的伪距和载波相位观测值分别用Prs和φrs表示,伪卫星观测方程为:
| $ \left\{ \begin{align} &P_{r}^{s}=\rho _{r}^{s}+c\text{d}t_{r}^{s}+e_{r}^{s} \\ &\varphi _{r}^{s}=\rho _{r}^{s}+c\text{d}t_{r}^{s}+\lambda N_{r}^{s}+\varepsilon _{r}^{s} \\ \end{align} \right. $ | (1) |
式中,ρrs表示伪卫星-接收机几何距离;dtrs表示伪距和载波对应的接收机-伪卫星钟差;c表示光速;ers和εrs分别表示伪距和载波观测值噪声;Nrs表示载波相位观测值整周模糊度;λ表示对应的波长。
从式 (1) 可以发现伪距和载波观测方程除了整周模糊度项,其余项相同,这意味着只要整周模糊度参数一旦被正确求解,载波相位观测值可以转化为非常精确的距离观测值[11]。
由于式 (1) 中包含伪卫星和接收机钟差项,采用两个接收机和两颗伪卫星构成的站星双差观测方程为:
| $ \left\{ \begin{align} &P_{qr}^{ls}=\rho _{qr}^{ls}+e_{qr}^{ls} \\ &\varphi _{qr}^{ls}=\rho _{qr}^{ls}+\lambda N_{qr}^{ls}+\varepsilon _{qr}^{ls} \\ \end{align} \right. $ | (2) |
式中,
从式 (2) 中可以发现伪卫星需要估计的参数包括接收机坐标以及载波相位模糊度参数,采用EKF进行估计,待估参数记作x,对应的协方差矩阵为P,观测值向量为y,在历元tk时刻为:
| $ \left\{ \begin{align} & {{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(+)={{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(-)+{{\mathit{\boldsymbol{K}}}_{k}}({{\mathit{\boldsymbol{y}}}_{k}}-\mathit{\boldsymbol{h}}({{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(-))) \\ & \mathit{\boldsymbol{P}}(+)=(\mathit{\boldsymbol{I}}-{{\mathit{\boldsymbol{K}}}_{k}}\mathit{\boldsymbol{H}}({{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(-))){{\mathit{\boldsymbol{P}}}_{k}}(-) \\ & {{\mathit{\boldsymbol{K}}}_{k}}={{\mathit{\boldsymbol{P}}}_{k}}(-)\mathit{\boldsymbol{H}}({{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(-))\cdot \\ & {{(\mathit{\boldsymbol{H}}({{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(-)){{\mathit{\boldsymbol{P}}}_{k}}(-)\mathit{\boldsymbol{H}}{{({{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(-))}^{\rm{T}}}+\mathit{\boldsymbol{R}})}^{-1}} \\ \end{align} \right. $ | (3) |
式中,
| $ \left\{ \begin{align} & {{{\mathit{\boldsymbol{\hat{x}}}}}_{k+1}}(-)=\mathit{\boldsymbol{F}}_{k}^{k+1}{{{\mathit{\boldsymbol{\hat{x}}}}}_{k}}(+) \\ & {{\mathit{\boldsymbol{P}}}_{k+1}}(-)=\mathit{\boldsymbol{F}}_{k}^{k+1}{{\mathit{\boldsymbol{P}}}_{k}}(+)\mathit{\boldsymbol{F}}{{_{k}^{k+1}}^{\ \ \rm{T}}}+\mathit{\boldsymbol{Q}}_{k}^{k+1} \\ \end{align} \right. $ | (4) |
式中,Fkk+1和Qkk+1分别表示状态转移矩阵和辅助因子矩阵。
由于伪卫星室内空间较小,直接对式 (2) 中的ρqrls线性化,仍会存在一阶线性化截断误差。因此,在数据处理中,采用迭代的EKF来削弱其影响,即对观测值残差进行阈值判断或者直接给定迭代次数。
在利用EKF进行状态参数估计时,初始状态的给定非常重要,GNSS动态定位中,一般通过伪距单点定位给出接收机初始位置,而伪卫星伪距精度和钟差都较大,无法通过单点定位给出初始位置。另外,由于室内伪卫星位置固定,静态观测条件下观测值强相关,导致无法通过静态多历元来求解接收机初始位置,模糊度更无法准确求解。因此,较好的方法是将接收机固定在已知点上进行初始化,即利用给定已知点坐标以及对应的先验精度信息来完成模糊度的固定。
模糊度固定采用continuous方式,即当前历元模糊度固定信息在没有信号中断的情况下对下一历元进行较小噪声的紧约束,采用经典LAMBDA算法,通过Ratio值检验便可完成模糊度固定。载体运动过程中,利用其运动速度信息 (先验信息或者其他辅助测量方法得到) 来进行EKF初始坐标状态松约束,这样可以提高模糊度浮点解的精度和相应的Ratio值[12]。一旦卫星信号中断,可以在载体运动过程中有效地进行模糊度重新固定,从一定程度上提高伪卫星系统的抗干扰性。
2 实验与分析实验中采用的伪卫星型号为GSG-L1,最终可以输出包含C/A码的L1频段载波。双天线软件接收射频前端采用USRP,通过搭载合适的子板,可以捕获全系列GNSS信号。本套伪卫星系统采用型号为DBSRX的两块子板转载在USRP中,可以捕获800 MHz~2.4 GHz的信号。实验场所是面积为10 m×7 m的室内,在房间顶部共布设了5颗伪卫星,如图 1所示,5颗伪卫星天线的精确坐标预先采用全站仪室内测定。
 |
| 图 1 伪卫星天线布置 Figure 1 Distribution of Pseudolite Antennas |
2.1 实验1
在数据采集过程中,接收机接收到所有5颗伪卫星信号,没有出现信号中断情况,数据采样间隔为0.1 s,共980个历元,数据处理采用武汉大学独立研制的室内伪卫星实时动态定位PL-RTK软件。
在模糊度固定中,Ratio值随历元变化序列如图 2所示,将Ratio阈值设置为3,可以看出在经过短时间的静态初始化后,Ratio值一直保持大于3的状态。
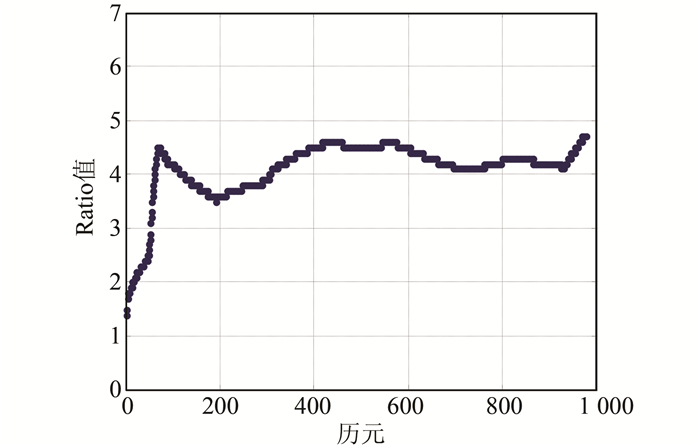 |
| 图 2 Ratio值变化序列 Figure 2 Value of Ratio |
此实验移动小车X/Y方向变化图如图 3所示,红色部分代表浮点解结果,蓝色代表固定解结果,经统计,模糊度固定率高达95.2%,可以看出X/Y变化曲线非常平稳,没有出现大的跳跃,和实验中移动小车走走停停的过程非常吻合。小车平面运行轨迹如图 4所示,颜色代表历元变化,可以非常直观地反映小车在整个实验中的运行轨迹。
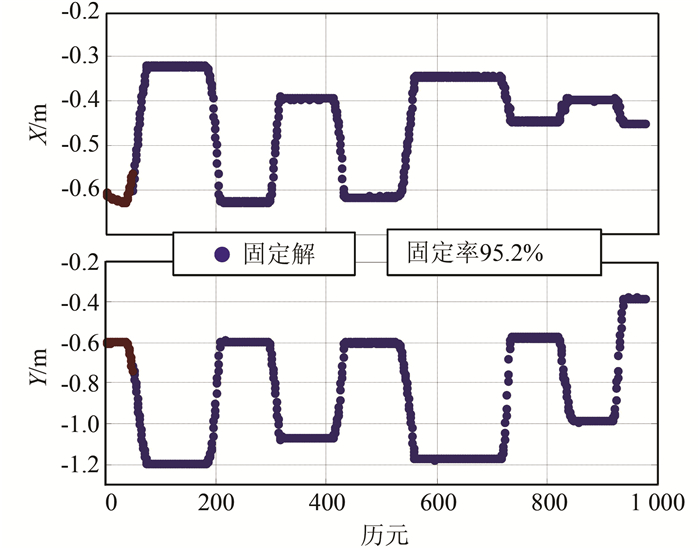 |
| 图 3 实验1移动小车X/Y方向变化序列 Figure 3 X and Y Direction Sequences of the Moving Car in Experiment 1 |
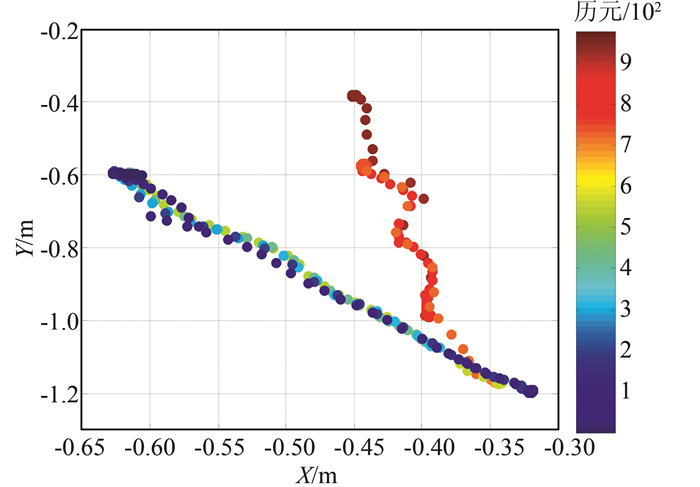 |
| 图 4 实验1移动小车平面运动轨迹图 Figure 4 Planar Trajectory of the Moving Car in Experiment 1 |
实验1利用本文方法求解的移动小车X方向坐标对应的中误差序列如图 5所示,可以看出,约在第50个历元,模糊度固定后,X方向对应的中误差迅速收敛,其最终精度在5 mm左右。
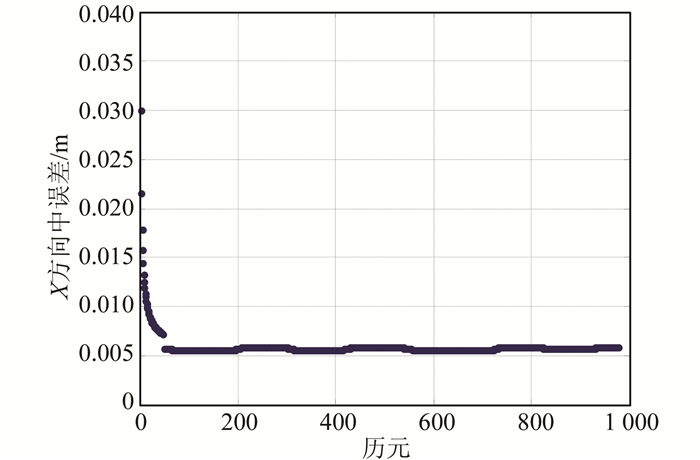 |
| 图 5 移动小车X方向求解中误差 Figure 5 X Direction Positioning Errors of the Moving Car |
2.2 实验2
小车在运行过程中,人为地进行了信号遮挡干扰,其观测伪卫星不再一直保持不变。可以发现,相对实验1,实验2中大部分时间只有4颗可视伪卫星,观测条件相对差一些,如图 6所示。图中绿色表示相应的Ratio值变化序列,阈值设置为2。
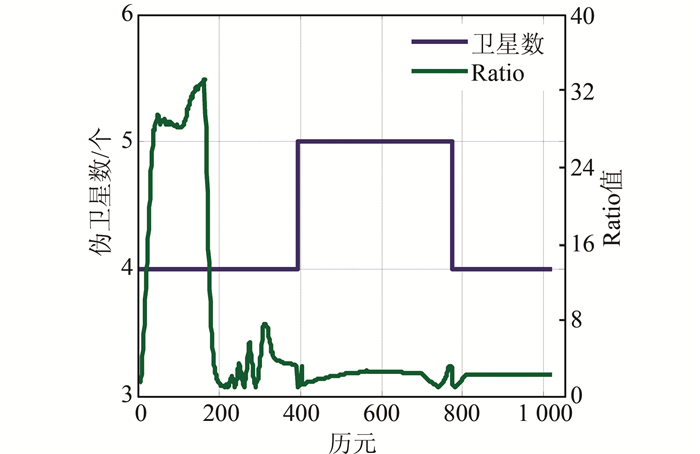 |
| 图 6 可视伪卫星数及Ratio值变化序列 Figure 6 Number of Visible Pseudolite Satellites and the Ratio Value |
移动小车X/Y方向变化序列如图 7所示,蓝色代表固定解,可以发现,经历10个历元模糊度得到固定,但在随后小车运行过程中,由于卫星数较少且信号强度不是很稳定,Ratio值出现小于2的情况,如对应的图中红色浮点解部分 (200历元附近),在400历元左右,由于多观测了一颗卫星,模糊度经过了短暂的重新初始化后又重新出现固定解,这一过程中对X方向解并没有造成大波动。在780历元左右,由于消失一颗可视卫星,模糊度固定失败,此时的浮点解相对于上一时刻出现了约8 cm的跳变,但随着历元的增加,模糊度又很快再次重新固定,X方向对应的曲线估计也恢复平顺状态。
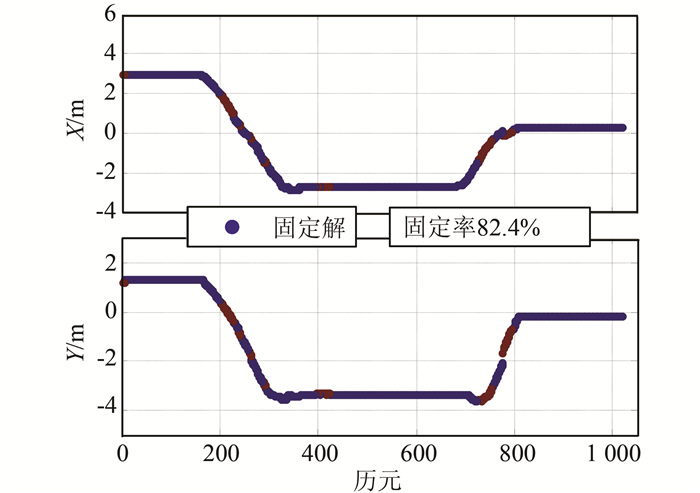 |
| 图 7 实验2移动小车X/Y方向变化序列 Figure 7 X and Y Direction Sequences of the Moving Car in Experiment 2 |
实验2移动小车的平面运行轨迹如图 8所示,可以看出整个过程中,除了在第780历元由于可视卫星数变少的前几十个历元,其运行轨迹出现了相对较大的波动,其余时间都非常平滑,说明了数据解算具有较高的精度和可靠性。
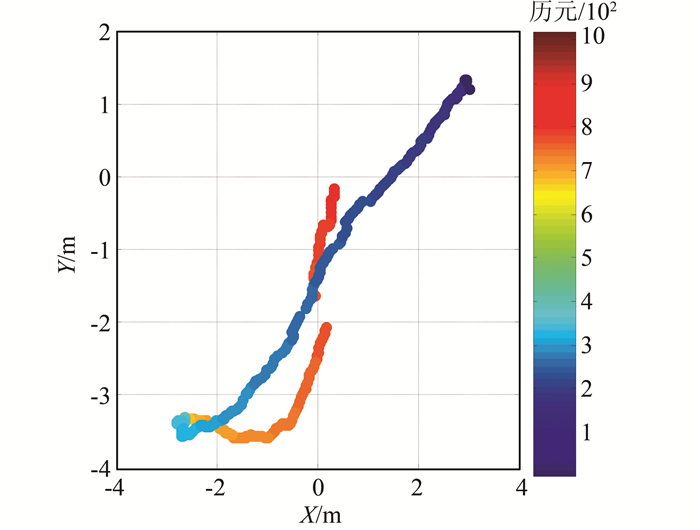 |
| 图 8 实验2移动小车平面运动轨迹图 Figure 8 Planar Trajectory of the Moving Carin Experiment 2 |
3 结束语
本文研究实现了一种基于固定点初始化的室内伪卫星动态定位方法,并通过两组实验验证了本套PL-RTK系统的性能,载波相位模糊度固定率较高,收敛精度约5 mm左右,并且在室内伪卫星信号受到干扰时,能够较快地实现模糊度重新固定,具备一定的抗干扰能力。
考虑到目前此套伪卫星室内定位系统必须在已知固定点进行初始化,对已知点精度要求较高 (10 cm),因此,下一步工作是实现米级精度固定点静态初始化或者任意点动态初始化的PL-RTK系统。
| [1] | Hofmann-Wellenhof B, Lichtenegger H, Collins J. Global Positioning System: Theory and Practice[J]. Journal of Navigation, 2001, 54(9): 1 283–1 296 |
| [2] | Wang J. Pseudolite Applications in Positioning and Navigation:Progress and Problems[J]. Journal of Global Positioning Systems, 2002, 1(1): 48–56 DOI: 10.5081/jgps |
| [3] | Rizos C, Roberts G, Barnes J, et al. Experimental Results of Locata: A High Accuracy Indoor Positioning System[C]. International Conference on Ind oor Positioning and Indoor Navigation, Zurich, Switzerland, 2010 |
| [4] | Kurz O, Mongrédien C, Rohmer G.A New Multipath Detection and Mitigation Approach for Pseudolite Systems[C]. International Technical Meeting of the Satellite Division, Nashville, Tennessee, 2013 |
| [5] | Zhang P, Sun F, Xu Y, et al. Indoor Pseudolite Positioning Based on Interferometric Measurement of Carrier Phase[C].China Satellite Navigation Conference, Changsha, 2016 |
| [6] | Wan X G, Zhan X Q, Du G. Carrier Phase Method for Indoor Pseudolite Positioning System[J]. Applied Mechanics and Materials, 2012, 130-134(37): 2 064–2 067 |
| [7] | Kao Weiwen, Tsai Chin-Lang. Carrier Phase Indoor Positioning Using Pseudolites and Relative Movements[J]. Journal of the Chinese Institute of Engineers, 2005, 28(28): 899–903 |
| [8] | Kee C, Kim J, So H, et al. Effect of the Error in Line of Sight Unit Vector on the Accuracy of GPS and Pseudolite Navigation System[J]. Computers and Mathematics with Applications, 2004, 48(5): 779–787 |
| [9] | 聂志喜, 王振杰, 欧吉坤, 等. 非线性基线长约束条件线性化近似对模糊度解算的影响[J]. 测绘学报, 2015, 44(2): 168–173 DOI: 10.11947/j.AGCS.2015.20130491 |
| [10] | 高为广, 潘娜娜, 张晓东. 改进的迭代EKF算法在伪卫星定位中的应用[J]. 测绘科学, 2008, 33(4): 73–75 |
| [11] | Li Xin, Guo Jiming, Zhou Lv. Performance Analysis of BDS/GPS Kinematic Vehicle Positioning in Various Observation Conditions[J]. Sensor Review, 2016, 36(3): 249–256 DOI: 10.1108/SR-12-2015-0198 |
| [12] | Kubo N. Advantage of Velocity Measurements on Instantaneous RTK Positioning[J]. GPS Solutions, 2009, 13(4): 271–280 DOI: 10.1007/s10291-009-0120-9 |
 2017, Vol. 42
2017, Vol. 42

