| 旋转轴直线度测量方法研究 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China
直线度测量是几何量计量领域里最基本、最重要的项目,它与尺寸精度、圆度和粗糙度统称为影响产品质量的4大要素[1]。直线度测量的方法大致分为以下两种:①直接采用具有高直线度的物体作为直线基准的测量方法,如光学准直法、高精度直线导轨法、激光干涉法等;②采用补偿修正,不依赖于高精度直线基准的间接测量法,如二点法、三点法等[2, 3]。
针对已经投入使用的工业设备,由于其所处现场环境复杂,遮挡比较严重,设备架设比较困难,直接采用具有高直线度的物体作为直线基准的测量方法在现场实施非常困难,因此,测量精度高和设站灵活的全站仪自由设站法就凸显出其优势[4]。
1 测量方案设计首先,建立高精度控制场;然后,通过自由设站确定测站的坐标,采用极坐标法确定旋转轴表面待定点的坐标;最后,拟合得到旋转轴的轴线坐标进行直线度分析。
1.1 建立高精度控制场根据现场情况,选择合适的位置布设控制点,控制点布设要均匀,尽量保证能够在一个测站完成对所有控制点的测量工作。用方向观测法测量所有的控制点,建立一个以全站仪中心为原点的局部坐标系下的高精度控制场。
1.2 自由设站选择合适的位置架设全站仪,保证全站仪能够观测到控制场中至少3个几何图形良好的控制点进行自由设站以及至少1个控制点作为检核点。当检核点的坐标较差小于某阈值时采用此测站信息,否则需重新进行自由设站,直到检核点校差满足要求为止。
1.3 极坐标法测量全站仪以一个控制点为后视点进行定向,将带有棱镜的千分卡座依次安放到旋转轴上选定的圆环断面,如图 1所示。按极坐标法对千分卡座上的棱镜进行测量,测量时要确保目标棱镜在视野范围内无任何遮挡。完成该测站数据采集后,搬动测站继续进行后方交会和数据采集,当旋转轴上选定的圆环断面上至少测量6个点且点位分布在不少于2/3个圆环上时,数据采集结束。
 |
| 图 1 带有棱镜的千分卡座 Figure 1 Micrometer Stand with Prism |
1.4 数据处理
得到所有圆环断面上测量点的坐标后,采用最小二乘拟合法对每个圆环上的点进行圆曲线拟合,确定每个圆环的圆心坐标和半径[5-7]。通过圆曲线拟合,可以拟合得到轴线一系列点的坐标,采用两端点连线法求解直线度误差[8]。
2 精度分析 2.1 自由设站精度分析全站仪自由设站法原理是在待定点上架设全站仪,测出待定点到已知控制点之间的距离和角度, 求解待定点坐标[9],如图 2所示。
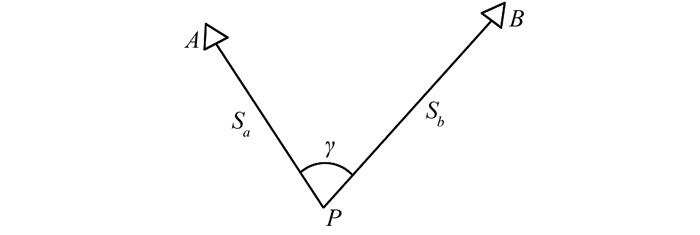 |
| 图 2 全站仪自由设站法示意图 Figure 2 Sketch Map of Total Station Free-Stationing |
以观测两个已知控制点为例,已知控制点A、B两点的坐标分别为 (XA, YA) 和 (XB, YB), 假设待定点P的坐标为 (XP, YP),观测了待定点P到两个已知点A、B的距离Sa、Sb及其夹角,采用条件平差得到P点平面坐标,根据误差传播定律可以得到P点平面坐标点位中误差为[10]:
| $ \begin{align} &m_{P}^{2}={{m}_{{{S}_{\alpha }}}}^{2}+\left( \frac{\hat{S}_{a}^{2}}{{{\rho }^{''2}}} \right){{\left( \frac{{{m}_{{{S}_{b}}}}}{{{{\hat{S}}}_{b}}} \right)}^{2}}{{\tan }^{2}}{{{\hat{\beta }}}_{A}}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \frac{\hat{S}_{a}^{2}{{\tan }^{2}}{{{\hat{\beta }}}_{A}}{{\cot }^{2}}\hat{\gamma }}{{{\rho }^{''4}}}m_{{\hat{\beta }}}^{2} \\ \end{align} $ | (1) |
式中,mSa和mβ分别为全站仪的测距中误差和测角中误差,前两项为测距误差对P点平面坐标点位中误差的影响,第三项为测角误差的影响。由于距离测量的相对中误差
| $ {{m}_{P}}\approx {{m}_{{{S}_{a}}}} $ | (2) |
待定点P的高程测量的原理是三角高程测量,对于自由设站的高程坐标精度分析如图 3所示。以观测两个已知控制点为例,已知控制点A、B两点的Z坐标ZA和ZB(均为相对Z坐标, 不考虑仪器高和目标高), 采用条件平差得到P点高程坐标,根据误差传播定律可以得到P点高程坐标中误差[11]为:
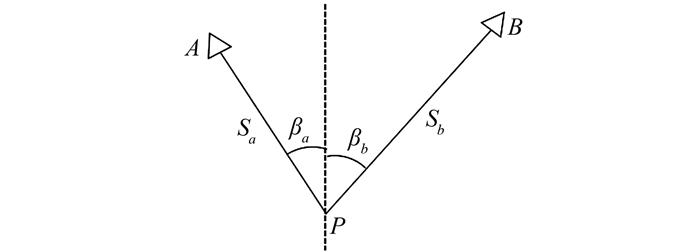 |
| 图 3 全站仪自由设站三角高程测量示意图 Figure 3 Sketch Map of Total Station Free-Stationing Trigonometric Leveling |
| $ {{m}^{2}}_{\left( {{Z}_{P}} \right)}={{\cos }^{2}}{{{\hat{\beta }}}_{a}}m_{{{{\hat{S}}}_{a}}}^{2}+\ \frac{\hat{S}_{a}^{2}{{\sin }^{2}}{{{\hat{\beta }}}_{a}}}{{{\rho }^{''2}}}m_{{{{\hat{\beta }}}_{a}}}^{2} $ | (3) |
式中,等号右边两项分别为测距中误差和测角中误差对P点高程坐标中误差的影响,第一项中
| $ {{m}_{\left( {{Z}_{P}} \right)}}\approx {{m}_{{{S}_{a}}}} $ | (4) |
当全站仪使用LeicaTM50(测角精度mβ=0.5″,测距精度mSa=0.6 mm+1×10-6时,由式 (2) 和式 (4) 可以得到P点的点位精度
全站仪极坐标法测量是通过两个通视的控制点定向,根据在控制点上观测待定点的角度和距离来确定待定点的坐标,如图 4所示。
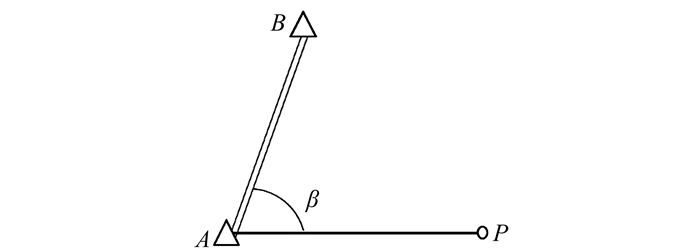 |
| 图 4 全站仪极坐标法示意图 Figure 4 Sketch Map of Total Station Polar Coordinate Method |
已知A、B的坐标分别为 (XA, YA, ZA) 和 (XB, YB, ZB),方位角为αAB,从测站A点对待测点P进行边角观测,得到AP的距离观测值SAP, 天顶距观测值βP和水平角度观测值β,极坐标法确定P点的坐标。将P点的坐标公式进行泰勒级数展开,根据误差传播定律可得:
| $ \begin{gathered} \mathit{\boldsymbol{K}} = \hfill \\ \left( {\begin{array}{*{20}{c}} 1 & 0 & 0 & {\sin {\beta _P}\cos \left( {{\alpha _{AB}} + \beta } \right)} & {{S_{AB}}\cos {\beta _P}\cos \left( {{\alpha _{AB}} + \beta } \right)} \\ 0 & 1 & 0 & {\sin {\beta _P}\sin \left( {{\alpha _{AB}} + \beta } \right)} & {{S_{AB}}\cos {\beta _P}\cos \left( {{\alpha _{AB}} + \beta } \right)} \\ 0 & 0 & 1 & {\cos {\beta _P}} & {-{S_{AB}}\sin {\beta _P}} \end{array}} \right. \hfill \\ \left. {\begin{array}{*{20}{c}} {-{S_{AB}}\sin {\beta _P}\sin \left( {{\alpha _{AB}} + \beta } \right)} & {{S_{AB}}\sin {\beta _P}\sin \left( {{\alpha _{AB}} + \beta } \right)} \\ {{S_{AB}}\sin {\beta _P}\cos \left( {{\alpha _{AB}} + \beta } \right)} & {{S_{AB}}\sin {\beta _P}\cos \left( {{\alpha _{AB}} + \beta } \right)} \\ 0 & 0 \end{array}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\left( {\begin{array}{*{20}{c}} {{\rm{d}}{x_P}} \\ {{\rm{d}}{y_P}} \\ {{\rm{d}}{z_P}} \end{array}} \right) = \mathit{\boldsymbol{K}} \times {\left( {{\rm{d}}{X_A}\;\;{\rm{d}}{Y_A}\;\;{\rm{d}}{Z_A}\;\;{\rm{d}}{S_{AP}}\;\;{\rm{d}}{\beta _P}\;\;{\rm{d}}{\alpha _{AB}}\;\;{\rm{d}}\beta } \right)^{\rm{T}}} \hfill \\ \end{gathered} $ | (5) |
根据误差传播定律与平差理论可得待定点P的坐标方差阵为:
| $ \left\{ \begin{align} & {{\mathit{\boldsymbol{D}}}_{P}}=\mathit{\boldsymbol{K}}\times {{\mathit{\boldsymbol{D}}}_{AP}}\times {{\mathit{\boldsymbol{K}}}^{\rm{T}}} \\ & {{\mathit{\boldsymbol{D}}}_{AP}}=\rm{diag}\left( \mathit{m_{{{X}_{A}}}}^{2}, \mathit{m_{{{Y}_{A}}}}^{2}, \mathit{m_{{{Z}_{A}}}}^{2}, \mathit{m_{{{S}_{AP}}}}^{2}, \mathit{m_{{{\beta }_{P}}}}^{2}, \mathit{m_{{{\beta }_{AB}}}}^{2}, \mathit{m_{\beta }}^{2} \right) \\ \end{align} \right. $ | (6) |
式中,mXA、mYA、mZA为测站点的坐标中误差;mSAP为测距中误差;mαAB为自由设站的定向角误差;mβP和mβ为天顶距和水平角的中误差[12-14]。
当全站仪使用LeicaTM50时,由前可知P点坐标中误差主要由仪器的测距中误差决定,测角中误差的影响可以忽略不计。有
当圆环断面上采集的点数为10个,分布在2/3个圆环上面,根据文献[7]给出的推导结果可以得到:圆环上采集的离散点的点位中误差为1.4 mm,采用最小二乘法拟合得到的圆曲线的圆心点的点位中误差约为离散点点位中误差的1/2,即0.7 mm,得到的圆曲线的半径的中误差约为离散点点位中误差的1/5,即0.3 mm。
3 案例分析某工厂的过滤系统位于地下约8 m×8 m×8 m的空间里,旋转滤网的重量约为20 T,整体重量着落在主轴轴承上,主轴长约5.92 m。
该设备自2005年左右投运后未做过相关的检测工作,本次测量目的是检测设备主轴的直线度,要求测点精度优于1.5 mm。主轴两端的对称空间基本相同,主轴中间是半径为9 m的旋转滤网,等间隔地分布着浮条,整个测量空间比较狭小,遮挡比较严重。现场控制点的布设和测站的架设如图 5所示。图中,三角形标志表示控制点位置,圆形标志表示测站位置,现场一共布设了10个控制点,架设了5次测站。在测站S0上观测所有控制点,观测6个测回,建立高精度的控制场,S1~S4测站的自由设站信息和检核点坐标较差如表 1所示。
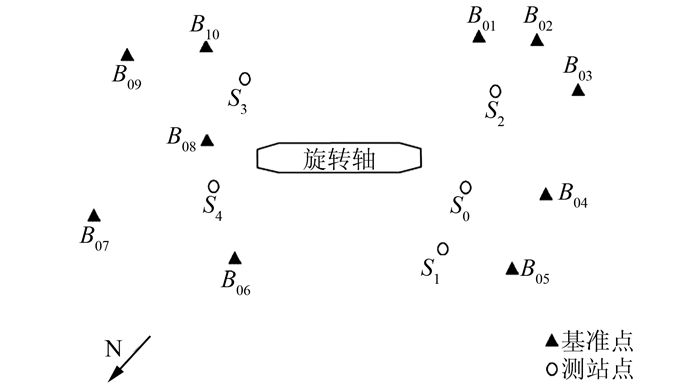 |
| 图 5 控制点及各测站点位示意图 Figure 5 Sketch Map of Reference Points and Station Points |
| 表 1 自由设站信息和检核点坐标较差/mm Table 1 Free-Stationing Information and Check Points Coordinates Discrepancy/mm |
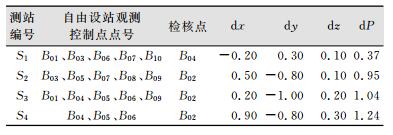 |
由表 1可知满足dP≤1.4 mm的要求,4个测站极坐标法测量的点位精度优于1.5 mm。旋转轴上每隔0.5 m布设一个圆环断面,一共选择了10个圆环断面。将带有棱镜的千分卡座依次安放到旋转轴上选定的圆环断面上,4个测站一共测量了91个点。将10个圆环断面上的点分别进行圆的拟合,如图 6所示。
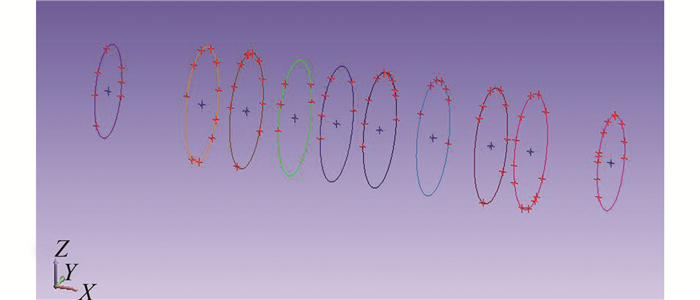 |
| 图 6 测量点位及最终拟合圆心位置示意图 Figure 6 Measuring Points and the Final Fitting Position of the Center of the Circle Sketch |
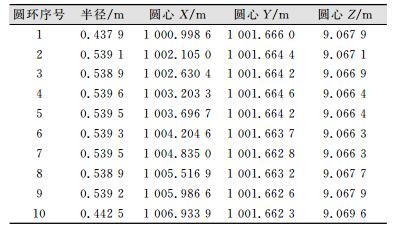
各圆环断面拟合得到的半径和圆心坐标如表 2所示。将各圆环断面拟合的半径结果与平均值求差可以得到各圆环断面拟合半径偏差[15],最大为0.4 mm。拟合圆环断面中半径的最大值与最小值之间的偏差为0.7 mm。此结果表明,本次测量数据精度高,拟合的圆心坐标数据可靠。采用两端点连线法求解直线度误差,即以首末两个圆环断面的圆心确定轴线,求得其余各圆环断面圆心至此轴线的偏差。最后结果为该旋转轴水平方向 (Y方向) 的偏差为±0.4 mm,垂直方向 (Z方向) 的偏差为±1.3 mm,整体最大偏距 (即旋转主轴的直线度公差) 为1.4 mm,如图 7所示。
| 表 2 各圆环的半径和圆心坐标 Table 2 Ring Radius and Center Coordinates |
 |
 |
| 图 7 旋转轴直线度结果图 Figure 7 Results of the Straightness of the Rotating Shaft |
4 结束语
本文提出的基于全站仪自由设站法的旋转轴直线度测量方法,在无法架设高精度基准测量条件下的直线度测量中十分实用和可靠,尤其在现场空间狭小、遮挡严重的环境下,充分凸显出了自由设站的灵活性和高精度,实现了对轴类被测件直线度的精确测量。
| [1] |
田瑞娟. 空间直线度测量方法的研究[D]. 成都: 四川大学, 2004 |
| [2] | 肖华杰, 范百兴, 西勤, 等. 激光跟踪仪动态测量在圆柱形导轨的直线度检测中的应用[J]. 工程勘察, 2015, 43(11): 70–73 |
| [3] | 余晓芬, 王鹏, 裴立明, 等. 大尺寸长轴二维直线度测量方法研究[J]. 中国机械工程, 2013, 24(14): 1 901–1 905 |
| [4] | 宋冶. 自由设站法三维变形观测精度的检测[J]. 工程勘察, 1999, (1): 61–63 |
| [5] | 徐国旺, 廖明潮. 拟合圆的几种方法[J]. 武汉工业学院学报, 2002, (4): 104–106 |
| [6] | 何凭宗. 圆曲线拟合及其在圆形立柱测量中的应用[J]. 测绘技术装备, 2001, 3(2): 13–15 |
| [7] | 陈明晶, 方源敏, 陈杰. 最小二乘和迭代法圆曲线拟合[J]. 测绘科学, 2016, 41(1): 194–197 |
| [8] |
尤林英. 直线度误差评定的方法和步骤[C]. 江苏省计量测试学会, 南京, 2009 |
| [9] | 张正禄. 工程测量学[M]. 武汉: 武汉大学出版社, 2005 |
| [10] | 胡菊英, 朱良文, 郭楠. 全站仪自由设站法及其精度分析[J]. 测绘与空间地理信息, 2014, (11): 179–181 DOI: 10.3969/j.issn.1672-5867.2014.11.056 |
| [11] | 张智韬, 黄兆铭, 杨江涛. 全站仪三角高程测量方法及精度分析[J]. 西北农林科技大学学报 (自然科学版), 2008, 36(9): 229–234 |
| [12] | 李巍, 赵亮, 张占伟, 等. 常用全站仪放样方法及精度分析[J]. 测绘通报, 2012, (5): 29–32 |
| [13] |
刘冠兰. 地铁隧道变形监测关键技术与分析预报方法研究[D]. 武汉: 武汉大学, 2013 |
| [14] | 孙立军, 刘兴春, 于兴超. 极坐标测量变形监测网稳定控制点组的检验[J]. 测绘信息与工程, 2009, 34(3): 25–26 |
| [15] | 黄富贵, 崔长彩. 评定直线度误差的最小二乘法与最小包容区域法精度之比较[J]. 光学精密工程, 2007, 15(6): 889–893 |
 2017, Vol. 42
2017, Vol. 42

