| 不同独立坐标系的比较以及最佳选取问题 |
2. 国家测绘地理信息局测绘标准化研究所,陕西 西安,710054
2. Research Institute of Standards of NASG, Xi'an 710054, China
国家有统一的坐标系统,从1954年北京坐标系、1980西安坐标系到当前的2000国家大地坐标系,坐标系统从定义到椭球参数都在不断地精化,更趋近于实际的地球。然而,国家坐标系是顾及全国及周边地区的一个大范围内的需求,由于我国幅员辽阔、地形起伏很大,国家坐标系不能满足各行各业、各个地区的需求,因此,为满足城市建设和工程建设需求,独立坐标系将长期存在并不断得到改进[1]。
每个城市都建立各自独立的坐标系为城市规划与各项工程服务。《城市测量规范》中规定:城市平面控制测量坐标系统的选择应以投影长度变形值不大于2.5 cm/km (相对投影变形小于1/40 000) 为原则[2]。因此,建立城市独立坐标系最主要的目的就是限制其长度变形。目前常用的城市独立坐标系有两类:① 投影于抵偿高程面上的高斯正形投影3°带的平面直角坐标系统 (简称抵偿坐标系);② 高斯正形投影任意带的平面直角坐标系统,投影面可采用黄海平均海水面或城市平均高程面 (简称任意带坐标系)。但是,随着旧城市的改造与扩建,新城市的不断涌现,城市面积日趋扩大,跨度也随之增加,若仍使用这两类坐标系,将不能满足精度要求。因此,本文将这两类坐标系结合在一起,建立投影于抵偿高程面的高斯正形投影任意带平面直角坐标系统 (简称抵偿任意带坐标系),而这在现行的《城市测量规范》中并没有明确规定。本文主要阐述这3类城市独立坐标系统建立的方法,分析它们的适用范围,然后利用算例对其进行比较分析,最后就独立坐标系的最佳选取提出合理化的建议。
1 独立坐标系建立与比较将地面上的观测结果归算到独立坐标系,其长度变形主要包括两个部分:① 将地面上的观测长度归算到参考椭球面所产生的高程归化改正ΔS1;② 将椭球面上的长度元素投影于高斯平面上所产生的投影变形ΔS2。两次归算产生的长度变形值称为总长度变形ΔS[3]。总长度变形可表示为:
| $\Delta S=\Delta {{S}_{1}}+\Delta {{S}_{2}}=-S\frac{{{H}_{m}}}{{{R}_{m}}}+S\frac{y_{m}^{2}}{2R_{m}^{2}}$ | (1) |
式中,Hm为基线端点平均大地高;Rm为边长区域的平均曲率半径;ym为边长在高斯平面上距离中央子午线垂距的平均值。设下面不同方法确定的独立坐标系为Oi坐标系。
1.1 抵偿坐标系抵偿坐标系是根据高斯投影改正选择一个合适的高程参考面作为整个测区的投影面,使得由此产生的高程归化改正抵偿高斯投影改正。简言之,确定抵偿坐标系的思想就是用适当的高程基准面以抵偿分带投影变形[4]。文献[4]推导出了投影变形与抵偿大地高之间的关系:
| $H={{H}_{m}}-\frac{y_{0}^{2}}{2{{R}_{m}}}$ | (2) |
式中,y0为完全抵偿点,即该点处总长度变形为0;H为抵偿大地高。
之前有不少学者研究确定y0方法,在此归纳为3种:
1) 传统确定方法[4]。选择最大横坐标处即y0=ymax,使得该处的高程归化改正ΔS1与投影变形ΔS2相等,那么该处就得到了完全的补偿。将y0=ymax代入式 (2) 中,就可以得到抵偿投影面的大地高为:
| $H={{H}_{m}}-\frac{y_{\max }^{2}}{2{{R}_{m}}}$ | (3) |
通过此方法求得的坐标系为O1坐标系。
2) 基于max (|ΔSi|)=min原则确定抵偿投影面[5]:
① 当测区位于3°带中央子午线一侧时,
| ${{y}_{0}}=\frac{\sqrt{2}}{2}\sqrt{y_{\max }^{2}+y_{\min }^{2}},H={{H}_{m}}-\frac{y_{\max }^{2}+y_{\min }^{2}}{4{{R}_{m}}}$ | (4) |
② 当测区跨越3°带中央子午线时,
| $\begin{align} & {{y}_{0}}=\pm \frac{\sqrt{2}}{2}\max \left( {{y}_{\max }},\left| {{y}_{\min }} \right| \right), \\ & H={{H}_{m}}-\frac{\max \left( y_{\max }^{2},y_{\min }^{2} \right)}{4{{R}_{m}}} \\ \end{align}$ | (5) |
通过此方法求得的坐标系为O2坐标系。
3) 基于ΣΔSi2=min原则确定抵偿投影面[6]:
| $\begin{align} & {{y}_{0}}=\pm \frac{\sqrt{3}}{3}\sqrt{y_{\max }^{2}+{{y}_{\max }}{{y}_{\min }}+y_{\min }^{2}}, \\ & H={{H}_{m}}-\frac{y_{\max }^{2}+{{y}_{\max }}{{y}_{\min }}+y_{\min }^{2}}{6{{R}_{m}}} \\ \end{align}$ | (6) |
通过此方法求得的坐标系为O3坐标系。
1.2 任意带坐标系任意带坐标系的中央子午线不再同国家3°带中央子午线重合,而是根据实际情况选择一条经线作为中央子午线,任意带坐标系把地面观测结果归算至参考椭球面。文献[7]给出了中央子午线计算的具体推导过程,其结论是中央子午线一般选在测区的中央,设y′0为平移后的新的y轴原点,那么y′0=(ymax+ymin)/2。任意带坐标系为O4坐标系。
1.3 抵偿任意带坐标系城市面积在扩大,东西跨度在不断增加,不少城市跨度已超过了100 km,甚至更宽。鉴于抵偿坐标系和任意带坐标系的局限性,为了保证测区范围内的相对长度变形仍然满足精度要求,因此将两类坐标系结合在一起,建立抵偿任意带坐标系。
文献[8]和文献[9]均对此坐标系的建立进行了相应的推导,但是有些参数定义不是很清楚且易于混淆,如y′0、y′min、y′max、yhalf、y0,并且抵偿面的确定仅考虑到ΔSi的平方和最小并不完整,因此本文在此基础上对参数进行了修改,并补充了抵偿面的确定方法,使推导过程及结果更加清晰、完整、容易理解。
选取y′0为平移后新的坐标系原点 (式中带有“′”的符号均代表在新坐标系下的坐标值),H0为投影面与归算边平均高程面的距离差 (H0=Hm-H),对于单位长度S=1 km,总长度变形可表示为:
| $\Delta {{S}_{i}}=\frac{{{H}_{0}}}{{{R}_{m}}}+\frac{{{\left( {{y}_{i}}-{{y}^{'}}_{0} \right)}^{2}}}{2R_{m}^{2}}$ | (7) |
由于式 (7) 中存在两个变量y′0和H0,且不存在具有实际意义的自由极值,所以难以求解。为了简化问题,可以先确定中央子午线使ΔSi2最小,然后再基于ΣΔSi2=min或者max (|ΔSi|)=min原则确定抵偿面。从§1.2可以知道,若使ΔSi2最小,对于整个测区而言,中央子午线应选在测区中央,即y′0=(ymax+ymin)/2。那么y′i=yi-y′0,y′max=|y′min|=ymax-y′0= (ymax-ymin)/2,y′max与y′min大小相等,符号相反。
1) 基于ΣΔSi2=min原则确定抵偿面
设y′完为新的坐标系中的完全抵偿点,那么可得:
| $\sum\limits_{i=1}^{n}{\frac{{{\left( {{y}^{'}}_{i}^{2}-{{y}^{'}}_{\text{完}}^{2} \right)}^{2}}}{4R_{m}^{4}}}=\min $ | (8) |
化简得:
| $\begin{align} & {{y}^{'}}_{\text{完}}=\pm \frac{\sqrt{3}}{3}{{y}^{'}}_{\max }=\pm \frac{\sqrt{3}}{6}\left( {{y}_{\max }}-{{y}_{\min }} \right), \\ & H={{H}_{m}}-\frac{{{\left( {{y}_{\max }}-{{y}_{\min }} \right)}^{2}}}{24{{R}_{m}}} \\ \end{align}$ | (9) |
按此方法求得的抵偿任意带坐标系为O5坐标系。
由|ΔS/S|<1/40 000,可得y′max<55.173 km,那么基于ΣΔSi2=min确定的抵偿任意带坐标系适用范围为城市跨度在110 km以内,基本上等同于1°分带的宽度。
2) 基于max (|ΔSi|)=min确定抵偿面
设y′完为新的坐标系中的完全抵偿点,由式 (5) 及y′max=|y′min|可得:
| ${{y}^{''}}_{0}=\frac{\sqrt{2}}{2}{{y}^{'}}_{\max },H={{H}_{m}}-\frac{{{\left( {{y}_{\max }}-{{y}_{\min }} \right)}^{2}}}{16{{R}_{m}}}$ | (10) |
按此方法求得的抵偿任意带坐标系为O6坐标系。
由|ΔS/S|<1/40 000,可得y′max<63.71 km,那么基于max (|ΔSi|)=min确定的抵偿任意带坐标系适用范围为城市跨度在127 km以内,明显扩大了测区的适用范围。
从上面的推导可以看出,抵偿任意带坐标系要比常用的两类城市坐标系适用范围更大,这样就可以确保在城市面积扩大、跨度增加等情况下,依然使得长度变形保持在精度范围以内。
1.4 独立坐标系之间的比较1) 抵偿坐标系
在抵偿坐标系中,只有中点的横坐标为y0,且位于平均高程面上的边长的长度变形才能完全抵消。假设某边长两端的平均高程为Hs,点的横坐标为y0+Δy,如果长度相对变形控制在精度指标内,那么可得:
| $\left| \frac{\Delta S}{S} \right|=\left| -\frac{{{H}_{s}}-H}{{{R}_{m}}}+\frac{{{\left( {{y}_{0}}+\Delta y \right)}^{2}}}{2R_{m}^{2}} \right|<\frac{1}{40\ 000}$ | (11) |
将式 (2) 代入式 (11),若地势较为平坦,可以忽略式 (11) 等式右边第1项的影响,可得:
| $\left| \frac{{{\left( {{y}_{0}}+\Delta y \right)}^{2}}}{2R_{m}^{2}} \right|<\frac{1}{40\ 000}$ | (12) |
可以看出,当y0距离中央子午线越远,那么Δy的范围也就越小,即所适用的测区跨度就越窄。因此一般大城市不适宜采用抵偿坐标系[10]。
2) 任意带坐标系
在任意带坐标系中所采用的投影面通常为城市平均高程面 (对于一般平坦地区),严格的讲, 应该是该测区的平均大地高面。因为这样可以使得测区的高程归化改正为零,且中央子午线附近的投影几乎也为零。如果长度相对变形控制在精度指标内,那么可以得到:
| $\left| \frac{\Delta S}{S} \right|=\left| \frac{\Delta {{y}^{2}}}{2R_{m}^{2}} \right|<\frac{1}{40\ 000}$ | (13) |
取Rm=6 371 km,可推算出Δy∈(-45.057 km, 45.057 km),即该坐标系适用于东西跨度约小于90 km的测区。
3) 抵偿任意带坐标系
根据§1.3的推导可以发现,抵偿任意带坐标系的适用范围为城市跨度在110~127 km之间,远大于前两类坐标系的适用范围。
2 算例分析为了便于比较O1~O6这6种独立坐标系,举一个算例来分析。某地区海拔Hm=2 km,最边缘距中央子午线100 km,S=1 km,测区范围y∈(-20 km, 100 km),取Rm=6 371 km,不同坐标系的长度变形结果如表 1所示。表中,①、②、③ 分别代表O1、O2和O3,④ 代表任意带坐标系O4,⑤ 和⑥ 代表抵偿任意带坐标系O5和O6;H为计算的抵偿面大地高,y0为计算的完全抵偿点。
建立城市独立坐标系的最主要目的就是减小高程归化改正与高斯投影变形产生的影响,将它们控制在一个微小的范围内,使得由坐标反算出来的长度与实测长度尽可能相符。图 1直观形象地表示了这6种城市坐标系的综合长度变形。
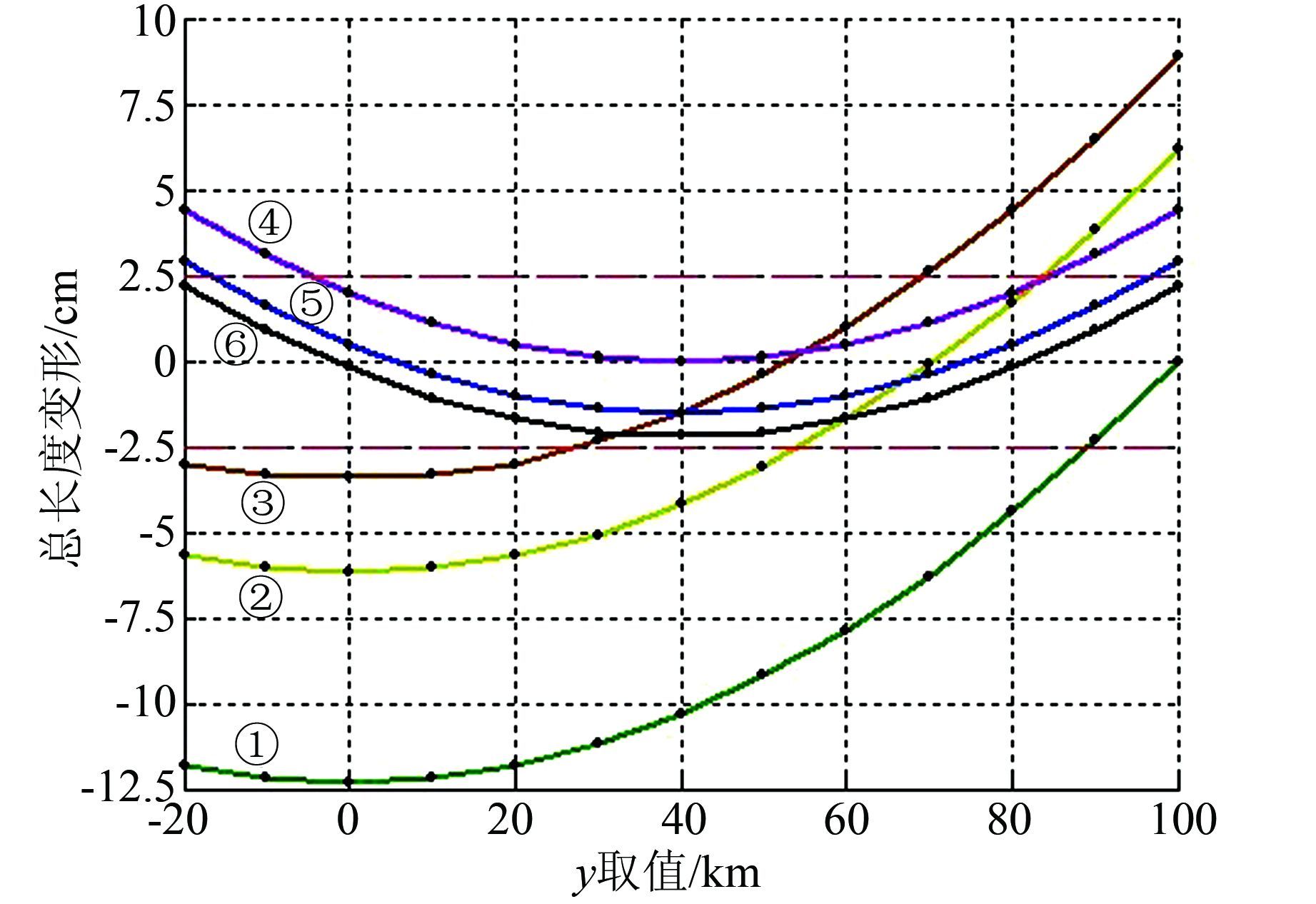 |
| 图 1 6种城市坐标系综合长度变形比较 Figure 1 Comparison of Comprehensive Length Deformation Between Six Kinds of Urban Coordinate Systems |
从表 1和图 1可以明显看出,基于不同方法建立的城市独立坐标系,其结果差异还是较大的。可以发现:
| 表 1 6种抵偿坐标系的长度变形 Table 1 The Length Deformation Between Six Kinds of Compensation Coordinate System |
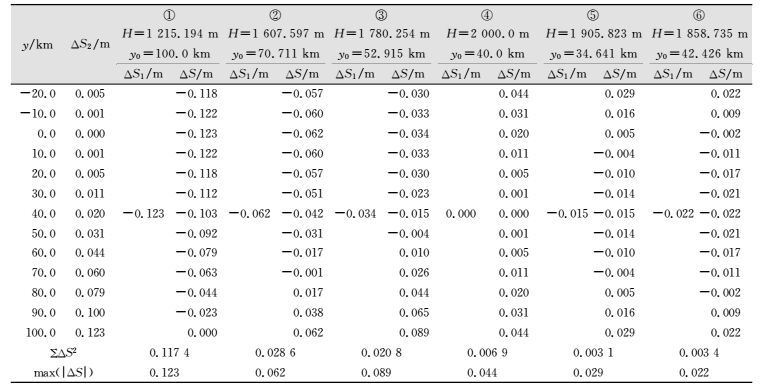 |
1) O1抵偿坐标系不能很好地处理综合长度变形,导致变形分配不均匀 (ΔS≤0),在中央子午线处变形最大。O2和O3抵偿坐标系要略优于O1,并且O3比O2理论依据更为充分,变形分配更为均匀,但是O2和O3大部分区域的综合长度变形均已超限。所以这3种抵偿坐标系对于小测区而言是可以的,但对于面积较大的测区则不适用。
2) O4任意带坐标系的适用范围为测区跨度不大于90 km,而实例的测区范围为120 km,所以在边缘地区长度变形也已超限。O5和O6抵偿任意带坐标系的综合长度变形值要远小于前4种,变形分布也较均匀,并且基本上都保证在精度范围以内。O5比O6理论依据更为充分,但O6比O5适用的测区跨度要更大。总体来看,O5和O6城市独立坐标系要优于前4种。
3 结束语1) 本文综述了不同城市独立坐标系统建立的方法,并对其进行了比较,分析了它们的适用范围。对抵偿任意带坐标系的推导过程进行修改,使结果更加清晰、容易理解。
2) 通过算例分析可以发现,在目前城区面积扩大、跨度增加的形势下,抵偿任意带坐标系要优于抵偿坐标系和任意带坐标系,它使得长度变形满足精度要求,便于各类工程的使用。
3) 笔者建议使用抵偿任意带坐标系作为城市的独立坐标系,因为它更好地控制了长度变形,满足《城市测量规范》要求,并且扩大了测区的适用范围,理论性强,易于编程实现。
| [1] | 刘继光, 房大为, 张凤录. 区域独立坐标系建立方法及变形分析[J]. 北京测绘, 2013, (5): 50–53 |
| [2] |
中华人民共和国住房与城乡建设部. CJJ/T 8-2011. 城市测量规范[S]. 北京: 中国建筑工业出版社, 2011 |
| [3] | 王淑玲, 刘振宇, 高炳浩. 利用最优化方法确定最佳城市独立坐标系[J]. 测绘科学技术学报, 2013, 30(6): 569–571 |
| [4] | 孔祥元, 郭际明. 控制测量学 (下)[M]. 武汉: 武汉大学出版社, 2001 |
| [5] | 范一中, 王继刚, 赵丽华. 抵偿投影面的最佳选取问题[J]. 测绘通报, 2000, (2): 20–21 |
| [6] | 王怀念. 最佳抵偿投影面的理论推导[J]. 测绘通报, 2004, (10): 18–19 DOI: 10.3969/j.issn.0494-0911.2004.10.007 |
| [7] | 范一中, 赵丽华. 任意带高斯正形投影直角坐标系的最佳选取问题[J]. 测绘通报, 2000, (8): 7–8 |
| [8] | 陈顺宝, 任建春, 亓月, 等. 抵偿任意带高斯投影平面坐标系选择的研究[J]. 测绘通报, 2005, (7): 21–23 |
| [9] | 何薇, 王广兴, 刘晖. 基于最佳抵偿法建立任意带坐标系的研究[J]. 测绘信息与工程, 2009, 34(6): 1–2 |
| [10] | 施一民. 建立区域坐标系问题的我见[J]. 测绘工程, 2000, 9(1): 38–41 |
 2017, Vol. 42
2017, Vol. 42

