| 基于CAD线框约束的建筑物三维激光点云建模 |
利用地面三维激光扫描可以快速、准确地进行三维重建[1],高质量的城市三维模型可以为政府规划、建筑整修等决策提供直观的技术支持。据此,相关学者[2-6]对激光点云三维建模的方法与流程进行了研究。但由于激光扫描得到的点云,数据量极其庞大,并含有噪声点,如果不对其加以约束处理,建模过程将需要大量人工操作,较为繁琐。因而探讨如何在保证精度的前提下既提高建模速度, 又减少人工工作量具有重要的意义。
随着数字化的深入,建筑物CAD数据获取较为方便,且精度高,但它不能表达物体表面的细节信息。因此,将两者结合,用CAD数据作为点云处理的约束条件,既能保证精度,提高建模效率,又可以反映细节,增加模型的真实性。本文以城市三维建模中最常见的建筑物建模为研究对象,提出一种基于CAD线框约束的点云建模方法,即通过一定的算法用CAD线框对散乱分布的点云数据进行约束,从而在保证模型精度的条件下提高建模速度。
1 基于CAD线框约束的点云建模算法综合利用CAD线框数据与点云数据,首先需将两者换算到同一坐标系下,进而通过计算点到直线的距离,选择合适的阈值,将距离较远的噪声点剔除,并将保留下来的点平移到建筑物边线上去,从而可以保证实际应用中同一平面上采集的点在点云空间中也分布于同一平面上。点云坐标与建筑物实际坐标一致,也为后续的建模工作奠定了基础,减少了工作量。整体工作流程如图 1所示。
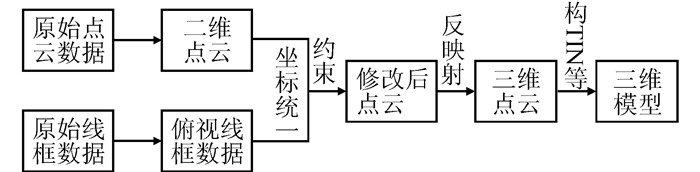 |
| 图 1 整体流程图 Figure 1 Flow Chart of Process |
1.1 坐标统一
目前激光扫描仪提供的点坐标是以仪器坐标系为基准的。仪器坐标系的坐标原点为扫描仪中心,X轴在水平扫描面内,Y轴在水平扫描面内与X轴垂直,Z轴与水平扫描面垂直。CAD线框数据通常采用全站仪采集得到。全站仪观测的坐标以相对坐标系或当地绝对坐标系为基准。不论哪一种,这两类坐标数据的数值都相差甚远,不能直接进行计算处理。因此,首先要进行坐标统一。将两数据投影到O-XY平面上,再利用旋转、平移、缩放三种变换方式实现变换,公式为:
| $ \left[\begin{array}{l} x'\\ y' \end{array} \right] = \lambda \left[{\begin{array}{*{20}{c}} {\cos \theta }&{-\sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[\begin{array}{l} x\\ y \end{array} \right] + \left[\begin{array}{l} \Delta x\\ \Delta y \end{array} \right] $ | (1) |
其中,(x, y)与(x′, y′)分别表示变换前和变换后的点坐标; θ为旋转角; λ为缩放系数,由于建筑物为刚体,故为1;Δx、Δy分别为X、Y方向上的平移系数。考虑到点云数据量大,保持点云固定,通过旋转、平移线框数据,使之与其套合。
旋转角的获得采用平行截线法,具体做法是选取模型的某条边,利用多条平行线,如y1=20,y2=30,…,yn=N,N取点云数据范围内的值,切割二维点云,分别获得对应的切割点,如(x1, y1),(x2, y2),…,(xn, yn),从而得到n-1个斜率k,ki=(yi+1-yi)/(xi+1-xi)(0 < i < n),最后取斜率的均值得到夹角。如图 2所示,三条水平实线代表平行截线,截得三个点,计算出两个夹角θ1与θ2,取均值。由于这个角度是相对于坐标轴而言的,因此,还需要计算出线框数据与坐标轴的夹角,这个角度直接利用某条线段的两个端点计算可得。最终旋转角为两夹角之和或之差。
 |
| 图 2 平行截线示意图 Figure 2 Sketch Map of Parallel Line |
旋转后的两类数据方向一致,因此只要知道某个点在点云数据与线框数据中的坐标即可得到平移系数。这个点可以是X或Y坐标的最小或最大点,也可以是对称建筑物的中心点,或者其他任何唯一的特征点。假设该点在两类数据中的坐标分别为(x1, y1)与(x2, y2),则有Δx=x2-x1,Δy=y2-y1。
1.2 点云约束首先确定一个阈值N,作为判断点是否属于该直线的依据。接着计算点云到线框直线的距离,由于离散点云拓扑关系未知,无法判断该点究竟属于哪一条直线,因此需要进行多次判断。
初始状态取所有的点构成待处理点群,计算点群中点与第一条待处理边的距离,如距离大于N,则不予以处理,这是由于无法确定该点究竟是噪声点还是其他较远边上的点。如图 3所示,对于黑色粗线标示出来的边,椭圆框圈出来的点到它的距离均大于N,但无法直接判断它们是噪声点还是其他边上的点。若小于N,则表明该点有可能在该边上,还要进一步判断是不是在与该边垂直的边上,如果是垂直边上的点, 仍不予以处理。如图 4所示,仍对黑色粗线边处理,椭圆框标记出的点既有在该条边上的,也有在与之垂直的邻边上的,需要进一步判断。经过判断后, 如果认为是该边上的,则将该点平移到直线上去,这样保证了所有的点在同一平面上,并且将该点从待处理点群中移除。
 |
| 图 3 距离大于N Figure 3 Distance Greater than N |
 |
| 图 4 距离小于N Figure 4 Distance Less than N |
第二次计算判断待处理点群中剩余点与第二条直线的关系,方法同上,依次进行, 直到最后一条边也被处理了。最后剩余未处理的则为噪声点, 被剔除。计算流程如图 5所示。
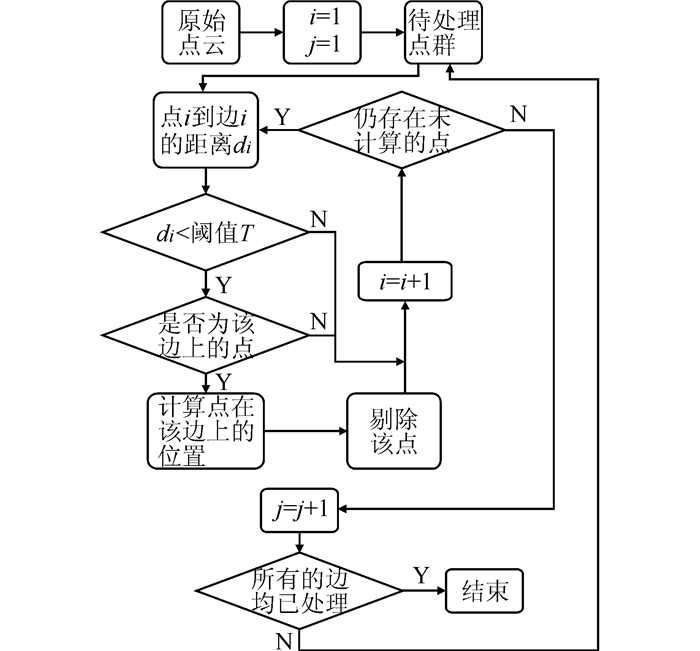 |
| 图 5 约束计算流程 Figure 5 Flow Chart of Constrained Computation |
2 实验分析 2.1 建筑物概况
本文对某建筑物进行建模操作,用FARO Focus3D S120获得三维激光扫描数据,分10站进行扫描,后期利用靶标法进行配准,共802 216个点,CAD线框数据由全站仪测得。如图 6所示。
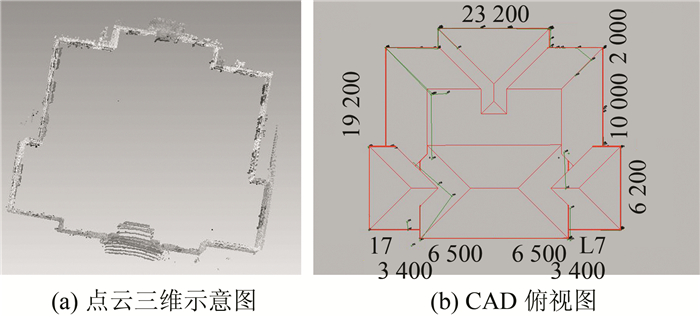 |
| 图 6 实例数据 Figure 6 Data of Example |
2.2 坐标变换
对点云数据进行O-XY平面的投影,即令Z=0,在约束计算结束后再投影回原始空间中,即重新给每个点赋予初始Z值。对CAD线框数据,取俯视图中角点处的二维坐标即可。
1) 旋转变换。
采用平行截线法,从y=25到y=80共做12条与X轴平行且间距相等的直线,如图 7平行实线所示。由于点云数据数量庞大等原因往往存在一个Y值对应多个X值的情况,因此需要找出合适的割点才能计算出正确的斜率。
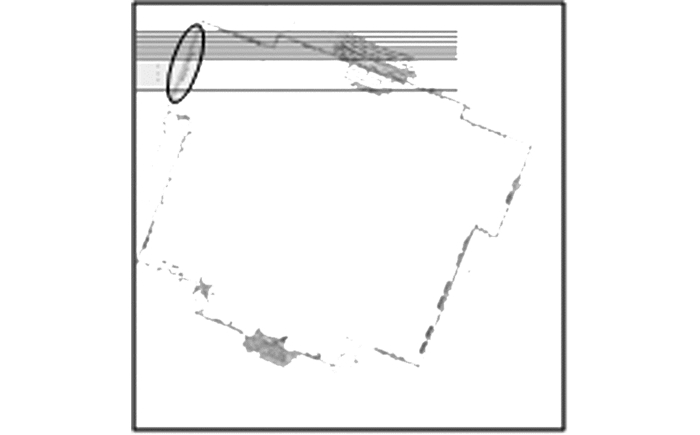 |
| 图 7 平行截线图 Figure 7 Parallel Line |
通过观察数据可以发现图 7中椭圆框标记出来的部分在其左侧没有噪声,因此在所有Y值相等的点集中选择X值最小的点作为合适的切割点,这样可以基本保证这些点在同一直线上。共可以得到12个点,计算出11个斜率。为了减弱误差影响,取算术平均值[7]作为结果。计算结果为k=0.360 5,对应角度θ=19°49′28″。而本例中线框数据与坐标轴方向一致,夹角为0,如图 8实线框所示,因此旋转角即为θ。旋转后结果如图 9所示。
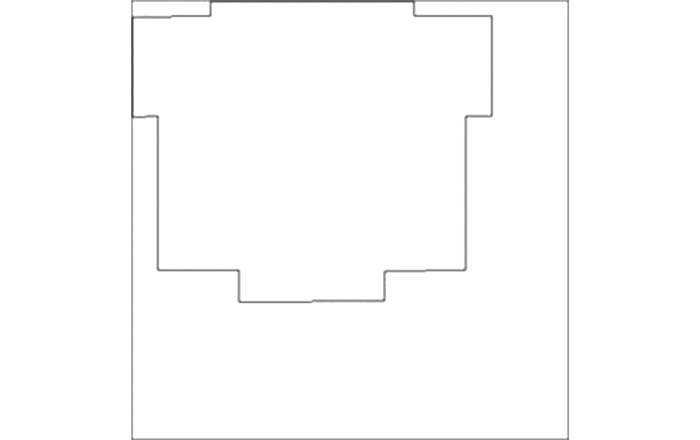 |
| 图 8 CAD线框图 Figure 8 CAD Wireframe |
 |
| 图 9 旋转结果图 Figure 9 Result of Rotation |
2) 平移变换。
先遍历点云数据,找出X坐标最小的点,同样可能存在多个这样的点,也即存在多个Y值,仍然取平均,得到(x1, y1);再遍历线框数据,找出X坐标为最小的点,同理,得到(x2, y2),Δx=x2-x1,Δy=y2-y1。坐标转换结果如图 10所示,黑色粗线为CAD线框图。由图 10可以看出,两类数据套合效果较好。
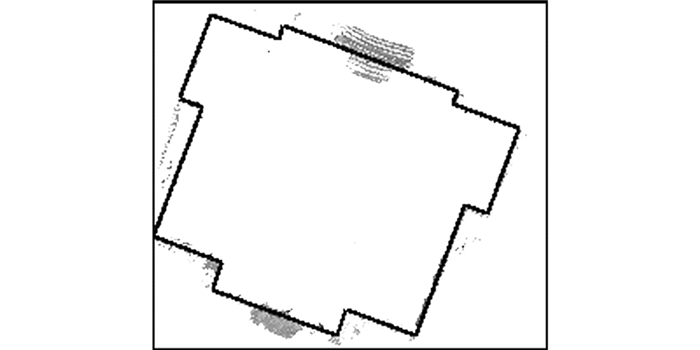 |
| 图 10 坐标变换后结果 Figure 10 Result of Coordinate Transformation |
2.3 约束计算
该建筑物有16个角点,取相邻两个点(Xi, Yi)与(Xi+1, Yi+1),可以构造直线方程:
| $ \frac{{Yi + 1-Yi}}{{Xi + 1-Xi}}X-Y + Yi - \frac{{Yi + 1 - Yi}}{{Xi + 1 - Xi}}Xi = 0 $ | (2) |
计算点(Xj, Yj)到直线的距离S为:
| $ \begin{array}{c} S = \left| {\frac{{Yi + 1-Yi}}{{Xi + 1-Xi}}Xj-Yj + Yi - \frac{{Yi + 1 - Yi}}{{Xi + 1 - Xi}}Xi} \right|/\\ \sqrt {{{\left( {\frac{{Yi + 1 - Yi}}{{Xi + 1 - Xi}}} \right)}^2} + 1} \end{array} $ | (3) |
多次实验表明,阈值选在2附近时,计算效果较好。因此,这里阈值选择2,S大于2不考虑,S小于2,进一步判断是否为垂直边上的点。判断方法有以下两种:①分别计算该点到与该直线相邻的两条直线距离,如均大于S,则认为是该直线上的点;②两直线垂直,斜率乘积必为-1。据此分别计算该点到直线两端点连线的斜率,再分别与该直线斜率相乘,若均不等于-1,则认为是该直线上的点。
如果判断该点属于该直线,则进一步将该点平移到直线上去,即寻找该点在直线上的垂足点,换算公式如下:令
| $ A = \frac{{Yi + 1-Yi}}{{Xi + 1-Xi}}, C = Yi-\frac{{Yi + 1 - Yi}}{{Xi + 1 - Xi}}Xi $ |
则有:
| $ \begin{array}{c} \left[ \begin{array}{l} Xj'\\ Yj' \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {1/\left( {1 + {A^2}} \right)}&{A/\left( {1 + {A^2}} \right)}\\ {A/\left( {1 + {A^2}} \right)}&{{A^2}/\left( {1 + {A^2}} \right)} \end{array}} \right]\left[ \begin{array}{l} Xj\\ Yj \end{array} \right] + \\ \left[ \begin{array}{c} - A \cdot \frac{C}{{1 + {A^2}}}\\ C/\left( {1 + {A^2}} \right) \end{array} \right] \end{array} $ | (4) |
若计算结果大于端点坐标,则用端点坐标代替。通过这个计算一方面可以保证端点处的点云坐标不会超出实际坐标范围;另一方面,后期做逆平移变换,可以将点云坐标换算至CAD坐标系下,即建筑物实际坐标,从而保证了精度要求。
重复操作16次,即所有边均有被处理过。运算结果如图 11所示。
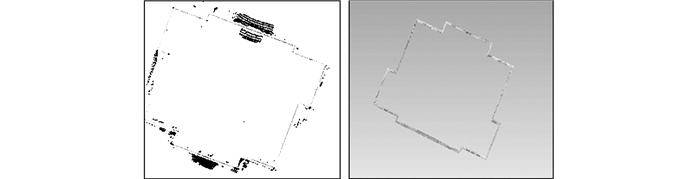 |
| 图 11 约束计算结果 Figure 11 Result of Constrained Computation |
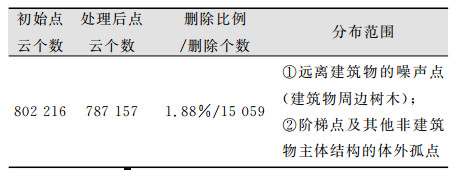
图 11(a)显示为二维点云运算结果,深色标记的是被剔除的噪声点,大致可以看出删除效果较好,相比于原始数据,分布更加平整;图 11(b)显示为修改后的三维点云数据。从表 1可以看出,预处理效果较好,删除结果仍能保持建筑物的特征不被丢失。
| 表 1 约束结果统计表 Table 1 Statistical Table of Constrained Computation Result |
 |
3 效果比较
下面分别对未经过约束处理和经过了约束处理的点云进行三维建模,并进行比较。
目前三维建模最常用的是构建三角面片,即Delaunay三角网,它是符合最小角最大准则、ABN准则等优化准则的唯一网格模型[8]。构网结果如图 12所示。
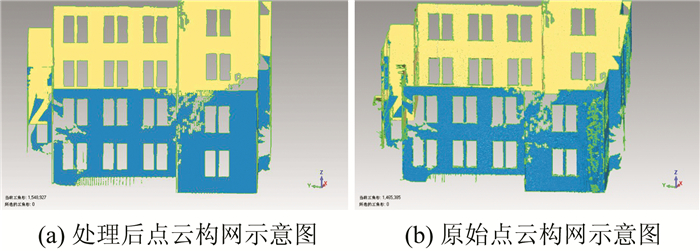 |
| 图 12 构网结果图 Figure 12 Result of Gridding |
图 12(a)为经过约束后点的构网结果,图 12(b)为原始数据构网结果,初步可见图 12(b)所显示的模型更粗糙,保留了许多错误细部,需要进一步删除。图 13为建筑物细部图,相比图 13(a)约束后的模型,图 13(b)可以看出明显的起伏变化,表明三角面片并不在同一平面中,且存在较多的冗余三角面片(图 13中椭圆标记出),而在部分区域(如窗框)本应连接的地方存在空洞(图 13中方框标记出)。
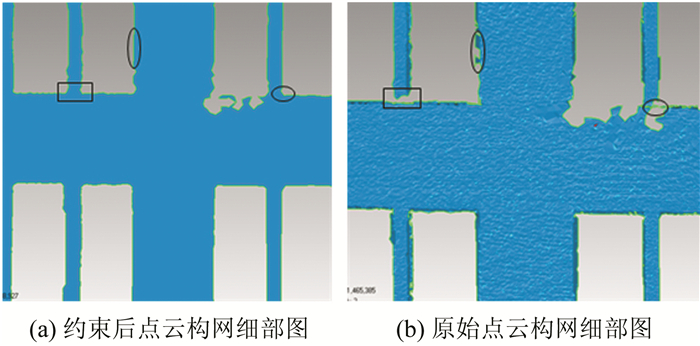 |
| 图 13 构网细部图 Figure 13 Details of Grid |
图 14展示了另一处细部图,图 14(a)仍为约束后点云建模结果。观察发现,图 14(b)显示出许多被实线分隔出来的块,如方框标记处所示,表明该区域存在重叠的三角网。这是因为采用多站扫描,导致同一区域可能有两站甚至三站点云,这些点从理论上来说是同一个面上的,但由于噪声以及其他原因,实际并不在同一个面上,在建模的时候会产生面片重叠的现象,并且有厚度。对于重叠区的修改是一个极其繁琐的工程,加剧了建模工作量,而且在人工修饰的过程中会有可能损失端点处的精度。
 |
| 图 14 构网细部图 Figure 14 Details of Grid |
由此可见,进行约束与未进行约束的点云建模结果差距较大,前者更适于模型的后处理,便于建模。
4 结束语本文提出一种基于CAD线框约束的建筑物三维激光扫描建模的方法。首先引入CAD线框模型,并获得点云的俯视图,然后通过坐标转换将两类数据统一到同一坐标系下,在此基础上计算点到线框的距离,利用距离判据将噪声点删除并将散乱分布的点约束到线上去,从而提高了封装结果的质量,有效避免了复杂繁琐的模型修改工作,减少了工作量,而且各个端点处都是CAD标准数据,提高了模型质量。实验结果亦表明,利用该算法进行点云预处理,可以获得较好的构网结果,方便后续操作。综合使用CAD数据与点云数据,可以在充分利用点云快速建模的优势前提下减少人工操作,缩短建模周期,节约成本,提高质量,在需要大量建筑物建模时效果尤佳。目前本算法主要适用于规则建筑物,如何将其扩展到不规则建筑物建模上去,有待进一步研究。
| [1] |
路兴昌, 张艳红. 基于三维激光扫描的空间地物建模[J].
吉林大学学报:地球科学版,2008,38(1) : 167–171.
Lu Xingchang, Zhang Yanhong. Spatial Object Modeling Based on 3D Laser Scanning Data[J]. Journal of Jilin University (Earth Science Edition),2008,38(1) : 167–171. |
| [2] |
宫丽玮, 张毅, 闫利. 基于Cyclone和PolyWorks的三维建模实现[J].
地理空间信息,2012,10(5) : 38–40, 49.
Gong Liwei, Zhang Yi, Yan Li. 3D Modeling Based on Cyclone and PolyWorks[J]. Geospatial Information,2012,10(5) : 38–40, 49. |
| [3] |
张毅.地面三维激光扫描点云数据处理方法研究[D].武汉:武汉大学, 2008 Zhang Yi. Research on Processing Method of Point Cloud from Terrestrial 3D Laser Scanning[D]. Wuhan: Wuhan University, 2008 |
| [4] |
吴静, 靳奉祥, 王健. 基于三维激光扫描数据的建筑物三维建模[J].
测绘工程,2007,16(5) : 57–60.
Wu Jing, Jin Fengxiang, Wang Jian. Three Dimensions Modeling of Buildings Based on Three Dimension Laser Scanner Data[J]. Engineering of Surveying and Mapping,2007,16(5) : 57–60. |
| [5] |
赵煦, 周克勤, 闫利, 等. 基于激光点云的大型文物景观三维重建方法[J].
武汉大学学报·信息科学版,2008,33(7) : 684–687.
Zhao Xu, Zhou Keqin, Yan Li, et al. 3D Reconstruction Method for Large Scale Relic Landscape from Laser Point Cloud[J]. Geomatics and Information Science of Wuhan University,2008,33(7) : 684–687. |
| [6] |
张巧英. 基于三维激光扫描的石佛院造像数字化测绘[J].
测绘地理信息,2014,39(6) : 42–46.
Zhang Qiaoying. Digital Surveying and Mapping of the Statues at Stone Buddha Temple Based on 3D Laser Scanning[J]. Journal of Geomatics,2014,39(6) : 42–46. |
| [7] |
王穗辉.
误差理论与测量平差[M]. 上海: 同济大学出版社, 2010 .
Wang Suihui. Error Theory and Surveying Adjustment[M]. Shanghai: Tongji University Press, 2010 . |
| [8] |
郑德华.三维激光扫描数据处理的理论与方法[D].上海:同济大学, 2005 Zheng Dehua. Theory and Method of Data Processing for 3D Laser Scanning[D]. Shanghai: Tongji University, 2005 |
 2016, Vol. 41
2016, Vol. 41

