| 基于对偶四元数描述的LiDAR点云解析配准算法 |
点云配准是空间三维建模的重要技术手段,配准的精度直接影响到空间三维建模的精度[1]。国内外对于LiDAR点云配准算法的研究主要分为迭代法与解析法。迭代法中经典算法是1992年由Besl和McKay提出的ICP(iterative closest point)算法[2]以及该算法的改进[3-5],基本思路是:有两个相邻点云集合,通过迭代方式在这两个点云中寻找最邻近点对,再利用迭代和最邻近点对求解坐标变换参数。点云配准的布尔莎7参数模型[6]是非线性模型,而对于迭代法方程的线性化是必然的,这在某种程度上会使配准精确下降;此外,迭代法中变换参数的初值选取对迭代收敛结果也有一定影响。迭代算法的缺点可归纳为:对两组点云的相对初始位置要求较高;算法中有迭代过程,算法效率不高;对初值的精确度要求较高。
解析法则避免了迭代法的不足之处,旋转矩阵是一种正交矩阵,基于正交矩阵的坐标变换算法[7]是一种传统的解析算法,利用矩阵方程的最小二乘最佳逼近正交解求解过程[8-10]求解旋转矩阵。但是该方法在求解坐标变换参数时是分步求解,有可能会造成误差累积的出现,影响配准精度,而基于单位四元数的点云配准方法[11, 12]也同样存在此问题。
研究表明,对偶四元数能够同时描述刚体的旋转和平移[13],在对偶四元数的基础上进行点云配准算法分析能够解决配准参数分步求解的问题,进一步提高配准精度。
1 点云配准与对偶四元数 1.1 点云配准基本原理点云配准实质是三维空间的坐标转换,常用的模型是布尔莎模型,该模型共采用7个参数,分别是3个旋转参数ωX、ωY、ωZ,也被称为3个欧拉角,3个平移参数TX、TY、TZ和1个尺度参数λ。
1.2 对偶四元数及几何意义形如A=a0+a1i+a2j+a3k的数为四元数,四元数能够表述三维转动[14],将一个矢量围绕一个方向按右手螺旋规则旋转一定角度变成另一个矢量,过程如图 1所示。
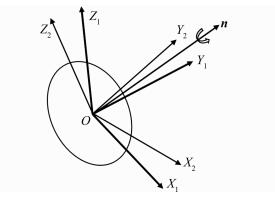 |
| 图 1 四元数表示的旋转变换过程 Figure 1 Quaternion-Based Rotation Transform |
形如
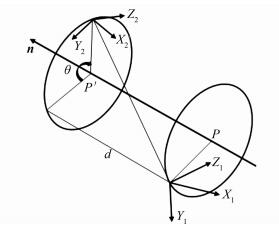 |
| 图 2 旋转平移的对偶四元数表示过程 Figure 2 Dual Quaternion-Based Rotation and Translation |
将
| $ \left[{\begin{array}{*{20}{c}} 1&{{{\bf{0}}^{\rm{T}}}}\\ {\bf{0}}&\mathit{\boldsymbol{R}} \end{array}} \right] = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right) $ | (1) |
式中,
| $ \begin{array}{l} \mathit{\boldsymbol{W}}\left( {\mathit{\boldsymbol{\dot r}}} \right) = \left[{\begin{array}{*{20}{c}} {{r_0}}&{-{\mathit{\boldsymbol{r}}^{\rm{T}}}}\\ \mathit{\boldsymbol{r}}&{{r_0}\mathit{\boldsymbol{E}}-\mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{r}} \right)} \end{array}} \right]\\ \mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right) = \left[{\begin{array}{*{20}{c}} {{r_0}}&{-{\mathit{\boldsymbol{r}}^{\rm{T}}}}\\ \mathit{\boldsymbol{r}}&{{r_0}\mathit{\boldsymbol{E}}-\mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{r}} \right)} \end{array}} \right]\\ \mathit{\boldsymbol{K}}\left( \mathit{\boldsymbol{r}} \right) = \left[\begin{array}{l} 0\;\;\;\;-{r_3}\;\;{r_2}\;\;\\ {r_3}\;\;\;\;0\;\;\;-{r_1}\\ -{r_2}\;\;{r_1}\;\;\;\;0 \end{array} \right] \end{array} $ |
结合对偶四元数的虚部,空间三维坐标的平移向量可以表示为:
| $ \mathit{\boldsymbol{\dot t}} = \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{\dot s}}, {{\mathit{\boldsymbol{\dot t}}}^{\rm{T}}} = \frac{1}{2}\left[{0\;\;{{\mathit{\boldsymbol{\dot t}}}^{\rm{T}}}} \right] $ | (2) |
设待配准的点云集合坐标系下的特征点为Xi(xi,yi,zi),用向量ri表示;基准点云集合坐标系下的特征点为XTi(xTi,yTi,zTi),用向量rTi表示,i=0,1,2, …, l表示两个点云集合中的第i对特征点,l表示两个点云集合的特征点对数。
坐标转换公式矢量化形式为:
| $ e_i^2 = {({{\mathit{\boldsymbol{\dot X}}}_{{T_i}}} - \lambda \mathit{\boldsymbol{W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot X}}}_i}\mathit{\boldsymbol{ + W}}{\left( {\mathit{\boldsymbol{\dot r}}} \right)^{\rm{T}}}\mathit{\boldsymbol{\dot s}})^2} $ | (3) |
运用最小二乘法思想,进行点云配准的结果就是使点云集合中所有特征点的误差平方和最小,即
| $ \begin{array}{*{20}{l}} {e_i^2 = {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {\lambda ^2}\mathit{\boldsymbol{\dot X}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot X}}}_i} + \mathit{\boldsymbol{\dot X}}_{{T_i}}^{\rm{T}}{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}} + 2\lambda {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot X}}}_i}} \right)\mathit{\boldsymbol{\dot r}} - }\\ { - 2{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}}} \right)\mathit{\boldsymbol{\dot r}}{\rm{ - 2}}\lambda {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}{{\left( {{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot X}}}_i}} \right)\mathit{\boldsymbol{\dot r}}} \end{array} $ | (4) |
将式(3)展开为:
| $ \begin{array}{l} e_i^2 = {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {\lambda ^2}\mathit{\boldsymbol{\dot X}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot X}}}_i} + \mathit{\boldsymbol{\dot X}}_{{T_i}}^{\rm{T}}{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}} + 2\lambda {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot X}}}_i}} \right)\mathit{\boldsymbol{\dot r}} - \\ - 2{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}}} \right)\mathit{\boldsymbol{\dot rQ}}{\left( {{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}}} \right)^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot X}}}_i}} \right)\mathit{\boldsymbol{\dot r}} \end{array} $ |
令
| $ \begin{array}{l} {\rm{ }}{\mathit{\boldsymbol{C}}_1} = - 2\sum\limits_{i = 1}^l {(Q{{\left( {{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{W}}\left( {{{\mathit{\boldsymbol{\dot X}}}_i}} \right))} \\ {\mathit{\boldsymbol{C}}_2} = 2\sum\limits_{i = 1}^l {\mathit{\boldsymbol{W}}{{\left( {{{\mathit{\boldsymbol{\dot X}}}_i}} \right)}_i}}, {\rm{ }}{\mathit{\boldsymbol{C}}_3} = - 2\sum\limits_{i = 1}^l {Q\left( {{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}}} \right)} \\ {C_4} = \sum\limits_{i = 1}^l {(\mathit{\boldsymbol{\dot X}}_i^{\rm{T}}{{\mathit{\boldsymbol{\dot X}}}_i}), } {\rm{ }}{C_5} = \sum\limits_{i = 1}^l {(\mathit{\boldsymbol{\dot X}}_{{T_i}}^{\rm{T}}{{\mathit{\boldsymbol{\dot X}}}_{{T_i}}})} \end{array} $ |
代入式(4)中得:
| $ \begin{array}{l} F\left( {\lambda, \mathit{\boldsymbol{\dot r}}, \mathit{\boldsymbol{\dot s}}} \right) = \\ \sum\limits_{i = 1}^l {\parallel {{\mathit{\boldsymbol{\dot X}}}_{{T_i}}} - \lambda \mathit{\boldsymbol{W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left( {\mathit{\boldsymbol{\dot r}}} \right){{\mathit{\boldsymbol{\dot X}}}_i}\mathit{\boldsymbol{ - W}}{{\left( {\mathit{\boldsymbol{\dot r}}} \right)}^{\rm{T}}}\mathit{\boldsymbol{\dot s}}{\parallel ^2} = } \\ l{\mathit{\boldsymbol{\dot s}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {\lambda ^2}{C_4} + {C_5} + \lambda {\mathit{\boldsymbol{\dot s}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {\mathit{\boldsymbol{\dot s}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_3}\mathit{\boldsymbol{\dot r}} + \lambda {\mathit{\boldsymbol{\dot r}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_1}{\mathit{\boldsymbol{\dot r}}^{\rm{T}}} \end{array} $ |
结合对偶四元数的两个限制条件式建立拉格朗日方程为:
| $ \begin{array}{l} F = l{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {\lambda ^2}{C_4} + {C_5} + \lambda {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_3}\mathit{\boldsymbol{\dot r}}+ \\ \lambda {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{C_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} + {\lambda _1}\left( {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}} - 1} \right) + {\lambda _2}\left( {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}}} \right) \end{array} $ | (5) |
F分别对λ、
| $ \partial F/\partial \lambda = 2\lambda {C_4} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{C_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} = 0 $ | (6) |
| $ \begin{array}{l} \partial F/\partial \mathit{\boldsymbol{\dot r}} = {\rm{ }}\lambda \mathit{\boldsymbol{C}}_2^{\rm{T}}\mathit{\boldsymbol{\dot s}} + \mathit{\boldsymbol{C}}_3^{\rm{T}}\mathit{\boldsymbol{\dot s}} + \\ \lambda \left( {{\mathit{\boldsymbol{C}}_1} + \mathit{\boldsymbol{C}}_1^{\rm{T}}} \right)\mathit{\boldsymbol{\dot r}} + 2{\lambda _1} + {\lambda _2}\mathit{\boldsymbol{\dot r}} = 0 \end{array} $ | (7) |
| $ \partial F/\partial \mathit{\boldsymbol{\dot s}} = 2l\mathit{\boldsymbol{\dot s}} + \lambda {\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {\mathit{\boldsymbol{C}}_3}\mathit{\boldsymbol{\dot r}} + {\lambda _2}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} = 0{\rm{ }} $ | (8) |
式(8)乘
| $ \mathit{\boldsymbol{\dot s}} = - \frac{1}{{2l}}\left( {{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {\mathit{\boldsymbol{C}}_3}\mathit{\boldsymbol{\dot r}}} \right) $ | (9) |
由式(6)得比例因子λ:
| $ \lambda = - \frac{1}{{2{C_4}}}\left( {{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}} \right) $ | (10) |
将式(9)代入式(10)得:
| $ \lambda = - \frac{1}{{2{C_4}}}\left( {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} - \left[{\frac{1}{{2l}}\left( {\lambda {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{C}}_2^{\rm{T}}\mathit{\boldsymbol{C\dot r}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{C}}_3^{\rm{T}}\mathit{\boldsymbol{\dot r}}} \right)} \right]} \right) $ | (11) |
令C2TC2=C22E,对式(11)进行整理得:
| $ \lambda = \frac{{( - {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} + \frac{1}{{2l}}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{C}}_3^{\rm{T}}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}})}}{{2{C_4} - \frac{{{C_{22}}}}{{2l}}}} $ | (12) |
将式(9)代入式(7)得:
| $ \begin{array}{l} \frac{{\partial F}}{{\partial \mathit{\boldsymbol{\dot r}}}} = \{ \lambda \left( {{\mathit{\boldsymbol{C}}_1} + \mathit{\boldsymbol{C}}_1^{\rm{T}}} \right) - \\ \lambda \mathit{\boldsymbol{C}}_2^{\rm{T}}\left( {\frac{{\lambda {\mathit{\boldsymbol{C}}_2} + {\mathit{\boldsymbol{C}}_3}}}{{2l}}} \right) - \mathit{\boldsymbol{C}}_3^{\rm{T}}\left( {\frac{{\lambda {\mathit{\boldsymbol{C}}_2} + {\mathit{\boldsymbol{C}}_3}}}{{2l}}} \right) + 2{\lambda _1}\} \mathit{\boldsymbol{\dot r}} = 0 \end{array} $ | (13) |
令C3TC3=C33E,式(13)化简得:
| $ \begin{array}{l} \frac{{\partial F}}{{\partial \mathit{\boldsymbol{\dot r}}}} = 2\left\{ { - \frac{1}{{4l}}} \right.\left( {{\lambda ^2}{C_{22}} + {C_{33}}} \right)\mathit{\boldsymbol{E}} - \\ \left. {\frac{\lambda }{2}\left[{\frac{1}{l}\mathit{\boldsymbol{C}}_2^{\rm{T}}{C_3}-\left( {{\mathit{\boldsymbol{C}}_{\rm{1}}}\mathit{\boldsymbol{ + C}}_1^{\rm{T}}} \right) + {\lambda _1}} \right]\mathit{\boldsymbol{\dot r}}} \right\} = 0 \end{array} $ | (14) |
设
根据矩阵特征值与特征向量的有关性质,对于4阶矩阵A,λ1为其特征值,
将式(7)乘
| $ \lambda {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} = - \frac{1}{2}\left( {\lambda {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{C}}_2^{\rm{T}}\mathit{\boldsymbol{\dot s}} + {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{C}}_2^{\rm{T}}\mathit{\boldsymbol{\dot s}}} \right) - {\lambda _1} $ | (15) |
将式(8)乘
| $ l{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} = - \frac{1}{2}\left( {\lambda {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_2} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_3}\mathit{\boldsymbol{\dot r}}} \right) $ | (16) |
将式(15)和式(16)代入到式(5)中,得:
| $ \begin{array}{l} F = l{{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}} + {\lambda ^2}{C_4} + {C_5} + \lambda {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_2}\mathit{\boldsymbol{\dot r}} + {{\mathit{\boldsymbol{\dot s}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_3}\mathit{\boldsymbol{\dot r}} + \\ \lambda {{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_1}{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}} + {\lambda _1}\left( {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot r}} - 1} \right) + {\lambda _2}\left( {{{\mathit{\boldsymbol{\dot r}}}^{\rm{T}}}\mathit{\boldsymbol{\dot s}}} \right) = \\ {\lambda ^2}{C_4} + {C_5} - {\lambda _1} \end{array} $ | (17) |
式中,当矩阵A取得最大正特征值时,F最小。对于矩阵A,
| $ {\lambda _\mathit{\boldsymbol{A}}} = \frac{1}{{4l}}\left( {{\lambda ^2}{C_{22}} + {C_{33}}} \right) + \frac{\lambda }{2}{{\lambda '}_\mathit{\boldsymbol{A}}} $ |
其中,λA是矩阵A的特征值;λ′A是矩阵A′的特征值。
矩阵A′是关于特征点3D坐标的矩阵,计算出矩阵A′的特征向量也就得出矩阵A的特征向量
计算过程如下:
1) 读取特征点原始数据(待配准点云集合中特征点的三维坐标(xi,yi,zi)、基准点云集合中特征点的三维坐标(xTi,yTi,zTi));
2) 由特征点坐标值计算C1、C2、C3、C4、C5,并由C1、C2、C3计算矩阵A′;
3) 求解矩阵A′的特征值与特征向量,得到矩阵A的特征向量
4) 由式(12)得到比例因子λ的值,由式(9)解出
5) 按照式(1)、式(2)分别计算旋转矩阵R和平移参数。
3 实验结果与分析为了验证本文提出的算法的正确性与有效性,在两组有重合区域的点云数据中分别找到8组与18组同名特征点,利用基于正交矩阵和对偶四元数两种算法对点云数据进行配准。配准结果如表 1所示,表中还列出了两组特征点基于正交矩阵的点云配准变换参数。通过对比发现,对于实际数据的解算,基于对偶四元数的算法能够正确求解,由于仪器误差和测量误差等系统误差偶然误差的存在,配准精度只能在一定的范围内,而且误差累积问题不足以显现出来,参数结果与基于正交矩阵的点云配准变换参数相差无几,但是从点云配准的参数求解推导过程中可以看出,该算法在求解参数时是同时求解的,不存在误差传播规律导致的误差累积问题。可以认为,将对偶四元数引入到点云配准算法中是可行的。
| 表 1 8组、18组特征点点云配准坐标变换参数 Table 1 Coordinate Transform Parameters of Point Cloud Registration from 8 Sets and 18 Sets Feature Points |
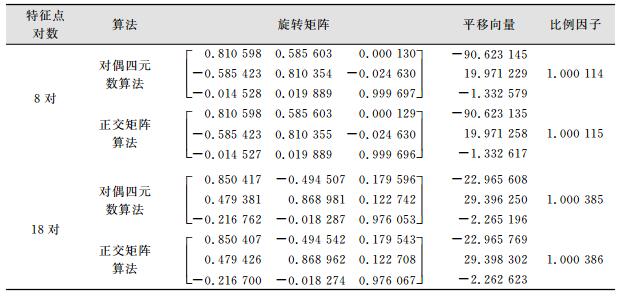 |
4 结束语
随着三维激光扫描技术的快速发展和成本的降低,该技术的应用领域越来越广泛,在测绘领域中也起着重要的作用,点云配准算法则是该技术的重点与基础。点云配准中应用广泛的算法是正交矩阵算法,该方法与ICP算法相比无需迭代,更加直接。基于对偶四元数的算法解决了基于正交矩阵和单位四元数算法在求解变换参数过程中参数分步求解的问题,避免了误差传播规律带来的累积误差出现的可能,理论上可以进一步提高配准精度,通过实验验证了该算法的可行性。
| [1] | 韩丽娜, 李缘廷. 融合地面激光扫描和摄影测量技术的三维重建[J]. 测绘地理信息, 2015, 40(3): 10–12 |
| [2] | Besl P J, McKay N D. A Method for Registration of 3-D Shapes[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 14(2): 239–256 |
| [3] | 周春艳, 李勇, 邹峥嵘. 三维点云ICP算法改进研究[J]. 计算机技术与发展, 2011, 21(8): 75–77 |
| [4] | 戴静兰, 陈志杨, 叶修梓. ICP算法在点云配准中的应用[J]. 中国图象图形学报, 2007, 12(3): 517–521 |
| [5] | 杨现辉, 王惠南. ICP算法在3D点云配准中的应用研究[J]. 计算机仿真, 2010, 27(8): 235–238 |
| [6] | 张宏. 布尔莎-沃尔夫转换模型的几何证明[J]. 测绘与空间地理信息, 2006, 29(2): 46–47 |
| [7] | Horn K P, Hilden H, Negahdariour S. Closed-Form Solution of Absolute Orientation Using Orthonormal Matrices[J]. Journal of the Optical Society of America, 1988, 5(7): 1 127–1 135 DOI: 10.1364/JOSAA.5.001127 |
| [8] | 张磊. 正交矩阵的反问题及其最佳逼近[J]. 湖南数学年刊, 1990, (Z1): 122–127 |
| [9] | 孟纯军, 胡锡炎. 对称正交矩阵反问题及其最佳逼近[J]. 计算数学, 2006, 28(3): 269–280 |
| [10] | 黄慕欢, 林茜. 正交矩阵在空间坐标变换中的作用[J]. 高等数学研究, 2009, 12(2): 24–26 |
| [11] | 王可伟, 岳东杰, 王性猛. 基于单位四元数的三维坐标转换新方法[J]. 测绘与空间地理信息, 2014, 37(11): 216–218 DOI: 10.3969/j.issn.1672-5867.2014.11.068 |
| [12] | 江刚武, 姜挺, 王勇, 等. 基于单位四元数的无初值依赖空间后方交会[J]. 测绘学报, 2007, 36(2): 169–175 |
| [13] | 张劲夫, 蔡泰信. 对偶四元数及其在刚体定位中的应用[J]. 黄淮学刊, 1993, 9(4): 27–30 |
| [14] | 刘俊峰. 三维转动的四元数表述[J]. 大学物理, 2004, 23(4): 39–43 |
| [15] |
屈昊. 基于对偶四元数的三维物体匹配方法的研究[D]. 哈尔滨: 哈尔滨工程大学, 2004 |
 2017, Vol. 42
2017, Vol. 42

