| 亚太地区GPS/GLONASS/Galileo/BDS组合实时精密单点定位性能评估 |
2. 中国铁路上海局集团有限公司工务处,上海,200071;
3. 高速铁路运营安全空间信息技术国家地方联合工程实验室,四川 成都,611756
2. China Railway Shanghai Group Co., Ltd, Shanghai 200071, China;
3. State-Province Joint Engineer Laboratory in Spatial Information Technology for High Speed Railway, Chengdu 611756, China
精密单点定位(precise point positioning, PPP)是一种基于全球导航卫星系统(Global Navigation Satellite System, GNSS)的高精度定位技术。使用一台接收机,利用国际GNSS服务(International GNSS Service, IGS)提供的精密卫星轨道和钟差产品,PPP可以在全球范围内为GNSS用户提供静态cm级到mm级、动态dm级到cm级的定位结果[1]。长期以来,PPP技术主要依赖于GPS,随着GLONASS、Galileo和BDS的发展,多系统组合PPP成为GNSS领域的一个研究热点[2-9]。多系统组合可以增加可见卫星数、改善卫星几何结构,从而缩短收敛时间、提高定位精度。
由于IGS最终产品有大约两周的延迟,而IGS快速产品有大约1d的延迟,导致PPP一般采用后处理模式。可以采用IGS超快产品的预测部分,实现实时PPP。但由于卫星钟差的短期波动性,导致卫星钟差产品外推时误差较大,采用这种方式实现的实时PPP性能较差。IGS实时试验计划(real-time pilot project, RTPP)在2013年正式提供实时服务(real-time service, RTS)。RTS产品包含实时卫星轨道和钟差改正值,是实现实时PPP的必要数据基础。目前,有几个分析中心可以提供RTS产品,大多只支持GPS单系统或者GPS/GLONASS双系统,CNES (Centre National d’Études Spatiales, France)提供的RTS产品可以支持4个GNSS系统(GPS、GLONASS、Galileo和BDS),因而本文采用其产品进行分析。
目前,在采用RTS产品进行实时PPP方面的研究报道相对较少。Zhang等[10]比较了采用不同分析中心RTS产品时GPS单系统实时PPP性能; Wang等[11]评估了全球尺度下GPS/GLONASS/Galileo/BDS组合实时PPP性能。目前,BDS仍处于全球部署阶段,BDS服务区外的可见卫星数很少。因此,本文只评估亚太地区四系统组合实时PPP性能,对静态和动态PPP均进行了分析。
1 GPS/GLONASS/Galileo/BDS组合实时PPP模型PPP通常采用伪距和载波相位观测值,两者表示如下:
| $ \begin{array}{c} P_{r}^{s}=\rho_{r}^{s}+t_{r}-t^{s}+I_{r}^{s}+T_{r}^{s}+b_{r}+b^{s} \end{array} $ | (1) |
| $\mathit{\Phi}_{r}^{s}=\rho_{r}^{s}+t_{r}-t^{s}-I_{r}^{s}+T_{r}^{s}+N_{r}^{s}+d_{r}+d^{s} $ | (2) |
式中,s表示GNSS卫星; r表示接收机; P是伪距观测值; Φ是载波相位观测值; ρ是接收机和卫星天线相位中心之间的距离; tr是接收机钟差; ts是卫星钟差; I是电离层延迟; T是对流层延迟; N是相位模糊度,br是接收机端伪距硬件延迟; bs是卫星端伪距硬件延迟; dr是接收机端相位硬件延迟; ds是卫星端相位硬件延迟。
通常采用消电离层组合消除一阶电离层误差。生成精密卫星钟差产品时,忽略了卫星端伪距硬件延迟,因而提供的精密卫星钟差改正值包含了两个不同频率上卫星端伪距硬件延迟的一个线性组合。对流层延迟通常可以分为干分量和湿分量两部分,干分量可以通过先验模型改正,湿分量需要作为待估参数进行估计。利用投影函数将斜延迟投影到天顶方向,只需估计一个天顶湿延迟,就能够显著减少待估参数数量、削弱参数之间的相关性。应用实时精密卫星轨道和钟差改正值后,伪距和载波相位消电离层组合观测值可以表示如下:
| $ \begin{array}{c} p_{r}^{s}=\mu_{r}^{s} \times X_{r}+t_{r , e}+m_{r}^{s} \times Z_{r} \end{array} $ | (3) |
| $ \varphi_{r}^{s}=\mu_{r}^{s} \times X_{r}+t_{r , e}+m_{r}^{s} \times Z_{r}+N_{r , e}^{s} $ | (4) |
式中,p和φ分别表示消电离层组合伪距和载波相位“观测值减去计算值”(observed minus computed, OMC); μ是视线方向的单位向量; X是接收机三维坐标; tr, e是接收机钟差估计值(包含了硬件延迟); m是湿映射函数,Z是对流层天顶湿延迟(zenith wet delay, ZWD); Ne是相位模糊度估计值(包含了硬件延迟)。
GPS/GLONASS/Galileo/BDS组合实时PPP观测模型可以表示如下:
| $ \left\{\begin{array}{l} p_{r}^{G}=\mu_{r}^{G} \times X_{r}+t_{r, e, G}+m_{r}^{G} \times Z_{r} \\ p_{r}^{R}=\mu_{r}^{R} \times X_{r}+t_{r, e, R}+m_{r}^{R} \times Z_{r} \\ p_{r}^{E}=\mu_{r}^{E} \times X_{r}+t_{r, e, E}+m_{r}^{E} \times Z_{r} \\ p_{r}^{C}=\mu_{r}^{C} \times X_{r}+t_{r, e, C}+m_{r}^{C} \times Z_{r} \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} \varphi_{r}^{G}=\mu_{r}^{G} \times X_{r}+t_{r, e, G}+m_{r}^{G} \times Z_{r}+N_{r, e}^{G} \\ \varphi_{r}^{R}=\mu_{r}^{R} \times X_{r}+t_{r, e, R}+m_{r}^{R} \times Z_{r}+N_{r, e}^{R} \\ \varphi_{r}^{E}=\mu_{r}^{E} \times X_{r}+t_{r, e, E}+m_{r}^{E} \times Z_{r}+N_{r , e}^{E} \\ \varphi_{r}^{C}=\mu_{r}^{C} \times X_{r}+t_{r ,e , C}+m_{r}^{C} \times Z_{r}+N_{r , e}^{C} \end{array}\right. $ | (6) |
式中,G、R、E、C分别表示GPS、GLONASS、Galileo、BDS卫星。由于各卫星系统接收机端的伪距硬件延迟不同,因而式(5)和式(6)中的4个接收机钟差参数各不相同。此外,由于GLONASS采用频分多址技术,采用不同频率因子的GLONASS卫星接收机端伪距硬件延迟会有所差异,即存在频率间偏差(inter-frequency Bias, IFB),导致接收机钟差参数不能完全吸收接收机端伪距硬件延迟。为了削弱这一影响,可以将GLONASS伪距观测值赋予较小的权,IFB的影响会体现在伪距残差中。
待估参数包括接收机三维坐标、4个接收机钟差、一个对流层天顶湿延迟以及和观测卫星数量相同的相位模糊度,可以表示如下:
| $ \begin{array}{c} \boldsymbol{S}=\left[X_{r}, t_{r, e ,G}, t_{r, e, R}, t_{r, e ,E}, t_{r, e, C}, Z_{r},\right. \\ \left.N_{r, e}^{G}, N_{r, e}^{R}, N_{r, e}^{E}, N_{r, e}^{C}\right]^{T} \end{array} $ | (7) |
式中,S表示估值向量。
可以利用误差传播定律确定观测值的随机模型。假设不同系统、不同卫星(同一系统)、不同类型(测码伪距和载波相位)、不同频率上的观测值不相关,对于任意一颗GNSS卫星,其观测值的方差协方差阵表示如下:
| $ \boldsymbol{Q}=\left[\begin{array}{cc} \left.a_{12,1}^{2}+a_{12,2}^{2}\right) \times\left(k_{1} / \sin e l\right)^{2} & 0 \\ 0 & \left(a_{12,1}^{2}+a_{12,2}^{2}\right) \times\left(k_{2} / \sin e l\right)^{2} \end{array}\right] $ | (8) |
| $ \left\{\begin{array}{l} a_{12,1}=f_{1}^{2} /\left(f_{1}^{2}-f_{2}^{2}\right) \\ a_{12,2}=f_{2}^{2} /\left(f_{1}^{2}-f_{2}^{2}\right) \end{array}\right. $ | (9) |
式中,f1表示L1/G1/ E1/ B1载波频率;f2表示L2/G2/ E5a/ B2载波频率;el是卫星高度角;k1和k2均为常数,分别表示伪距和载波相位观测值精度。
2 结果与分析 2.1 数据获取与处理策略IGS在2012年发起了MGEX(multi-GNSS experiment)。目前,MGEX跟踪网包含220多个测站,并且许多测站支持实时数据(观测值)获取。选取2017-04-08位于亚太地区的25个MGEX测站进行分析,这些测站均支持GPS、GLONASS、Galileo和BDS系统。表 1为四系统组合实时PPP具体的处理策略。
| 表 1 四系统组合实时PPP处理策略 Tab.1 Processing Strategies of Four-Constellation Integrated Real-Time PPP |
 |
2.2 实时精密卫星轨道和钟差产品精度评估
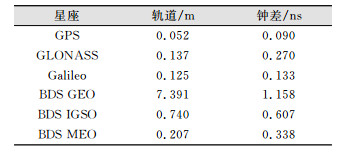
由于实时PPP的性能很大程度上依赖于使用的RTS产品,因而对实时精密卫星轨道和钟差改正值的精度进行了评估。将GfZ (Deutsches GeoForschungs Zentrum, Germany)提供的四系统混合最终产品作为参考。图 1和图 2分别为2017-04-08的实时精密卫星轨道和钟差改正值误差。从图中可知,GPS卫星轨道三维误差一般小于0.1 m,GLONASS(缩写为GLO)、Galileo(缩写为GAL)、BDS中圆地球轨道(MEO)卫星轨道3D误差则小于0.4 m,而BDS倾斜地球同步轨道(IGSO)和地球静止轨道(GEO)卫星轨道3D误差变化范围则分别高达1 m和10 m。需要注意的是,2017-04-08的RTS产品中只有一颗GEO卫星可用。对于大多数GPS和Galileo卫星,钟差误差在-0.3~0.3 ns之间变化; GLONASS和BDS MEO卫星的钟差误差在-1~1 ns之间变化。相较前两者,BDS IGSO和GEO卫星钟差误差的变化范围分别扩大了2倍和4倍。表 2为实时精密卫星轨道和钟差改正值误差RMS(Root Mean Square)统计值。从表 2中可知,GPS实时精密卫星轨道和钟差改正值精度分别为0.052 m和0.090 ns; Galileo卫星相应精度分别为0.125 m和0.133 ns。与GPS相比,GLONASS和BDS MEO卫星RTS产品精度分别下降了约3倍和4倍。BDS IGSO实时精密卫星轨道和钟差改正值精度分别为0.740 m和0.607 ns。由于BDS GEO卫星RTS产品精度太差,故在实时PPP解算中剔除了BDS GEO卫星。在具体的随机模型实现中,需要考虑各星座RTS产品的精度情况。
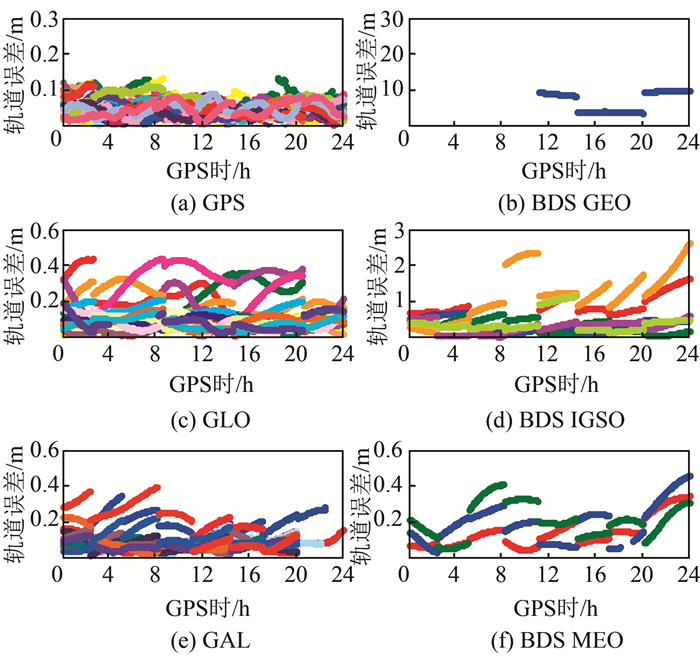 |
| 图 1 2017-04-08的实时精密卫星轨道改正值三维误差 Fig.1 3D Errors of Real-Time Precise Satellite Orbit Corrections on April 8, 2017 |
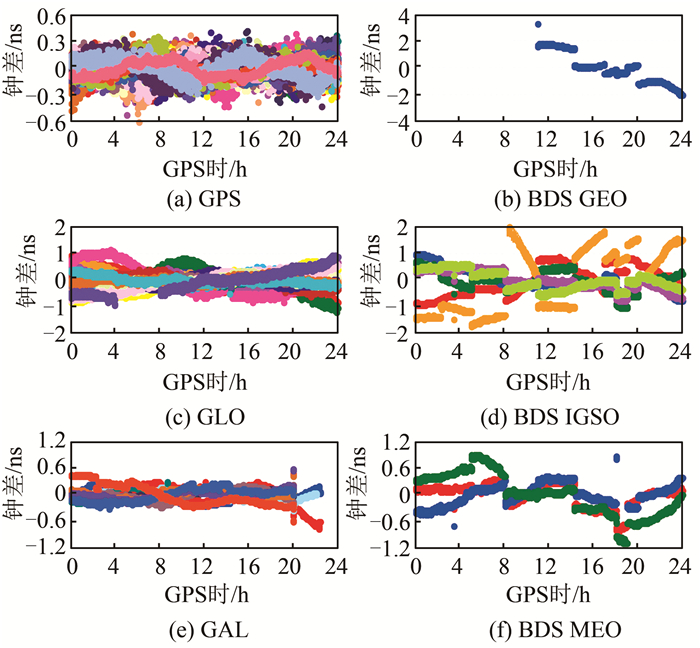 |
| 图 2 2017-04-08的实时精密卫星钟差改正值误差 Fig.2 Errors of Real-Time Precise Satellite Clock Corrections on April 8, 2017 |
| 表 2 实时精密卫星轨道和钟差改正值误差RMS统计值 Tab.2 RMS Values of Errors of Real-Time Precise Satellite Orbit and Clock Corrections |
 |
2.3 四系统组合实时PPP性能
为了进行对比分析,选择3种星座组合,即GPS单系统、GPS/GLONASS双系统、GPS/GLONASS/Galileo/BDS四系统。图 3为静态模式下不同观测时长的实时PPP定位精度。每个历元上的定位精度指的是该历元所有测站实时PPP定位误差的RMS统计值。从图 3中可知,随着观测时间不断延长,实时PPP的定位精度不断提高。在东方向,随着更多系统的数据参与计算,定位精度显著改善。而在其他两个方向,3种星座组合的解算结果比较一致。表 3为静态模式下实时PPP统计结果。收敛时间指的是图 3中定位误差收敛到0.1 m所需要的时间。统计了两种定位精度:①统计所有历元定位误差的RMS值,表征实时PPP整体精度情况; ②统计最后一小时定位误差的RMS值,表征其单日收敛精度。与GPS单系统相比,双系统组合收敛时间和定位精度(所有历元)在东、北、高3个方向分别改善了28%、19%、11%和6%、20%、7%。对于四系统组合实时PPP,3个方向的改善分别为43%、19%、26%和16%、25%、10%。在静态模式下,四系统组合实时PPP的单日收敛精度在3个方向分别为11.7 mm、8.0 mm、13.0 mm。
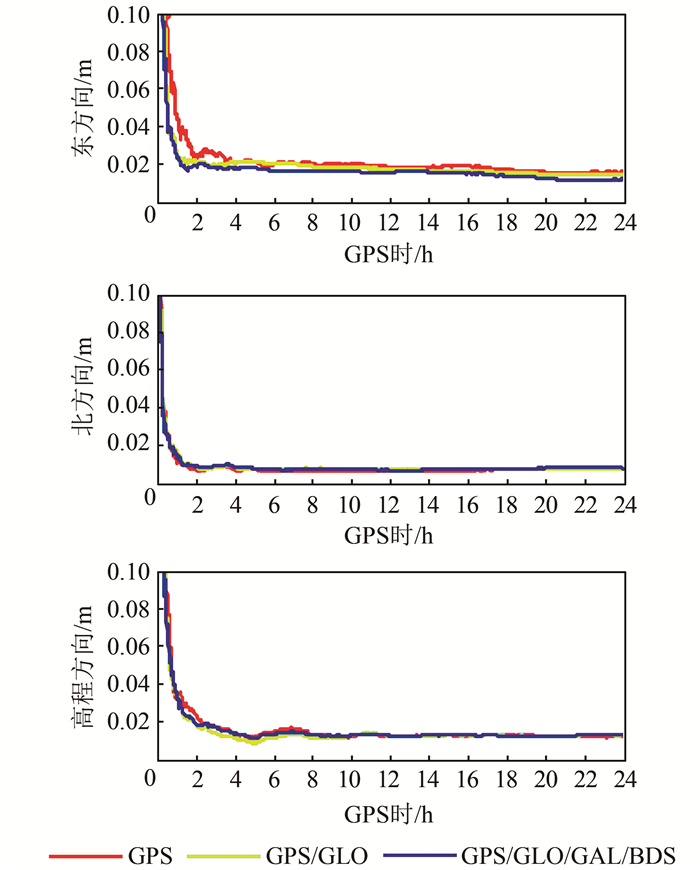 |
| 图 3 静态模式下不同观测时长的实时PPP定位精度 Fig.3 Real-Time PPP Positioning Accuracy for Different Observational Lengths in the Static Mode |
| 表 3 静态模式下实时PPP统计结果 Tab.3 Statistical Results of Real-Time PPP in the Static Mode |
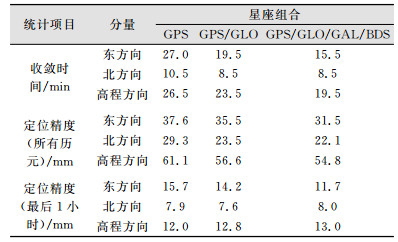 |
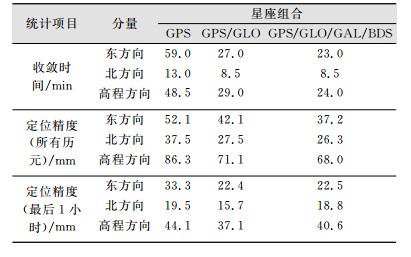
图 4和表 4给出了动态模式下实时PPP的相应结果。从图 4中可知,在大多数历元,多系统组合可以显著提高实时PPP动态定位精度。在位置解收敛后,实时PPP东方向和北方向上大多数历元的动态定位误差在4 cm之内变动,而高程方向的误差在8 cm之内变动。从表 4中可知,与GPS单系统实时PPP相比,GPS/GLONASS组合实时PPP的收敛时间在东、北、高3个方向改善了54%、35%、40%,定位精度(所有历元)在3个方向改善了19%、27%、18%。GPS/GLONASS/Galileo/BDS组合实时PPP与GPS单系统结果相比,相应的收敛时间改善为61%、35%、51%,相应的精度改善为29%、30%、21%。在动态模式下,四系统组合实时PPP收敛后3个方向的定位精度分别为22.5 mm、18.8 mm、40.6 mm。
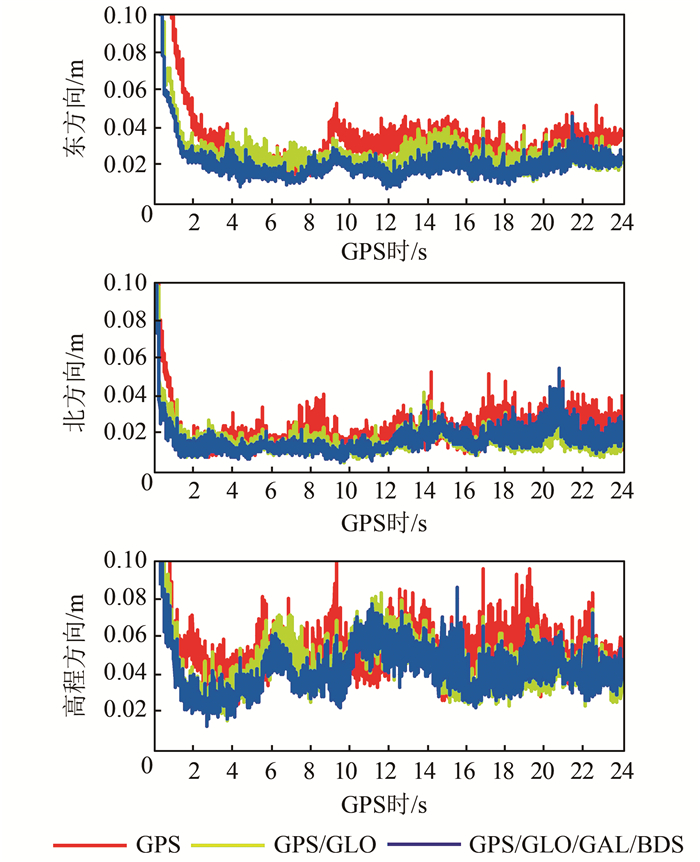 |
| 图 4 动态模式下不同观测时长的实时PPP定位精度 Fig.4 Real-Time PPP Positioning Accuracy for Different Observational Lengths in the Kinematic Mode |
| 表 4 动态模式下实时PPP统计结果 Tab.4 Statistical Results of Real-Time PPP in the Kinematic Mode |
 |
2.4 观测残差分析
观测残差中包含了测量噪声以及其他未模型化的误差,它可以作为重要指标来评估四系统组合实时PPP模型。图 5和图 6分别给出了静态模式下四系统组合实时PPP伪距和相位观测残差的分布。观测残差分析涉及了所有测站的结果。从图 5、图 6中可知,除GLONASS伪距观测残差外,其他所有观测残差均近似服从正态分布。图中还给出了观测残差的平均值和RMS统计值。GPS和BDS伪距观测残差在同一水平,分别为1.137 m和1.265 m。受IFB影响,GLONASS伪距观测残差最大,为1.958 m。Galileo伪距观测残差最小,为0.681 m。至于相位观测残差,GPS、GLONASS、BDS结果近似,分别为1.4 cm、1.5 cm、1.6 cm,而Galileo相位观测残差只有0.7 cm。Galileo拥有最小的残差,原因可能是Galileo可见卫星数较少,冗余观测不够。总之,4个卫星系统的观测残差均在可接受范围内,表明各种误差和偏差在四系统组合实时PPP模型中得到了很好的处理。
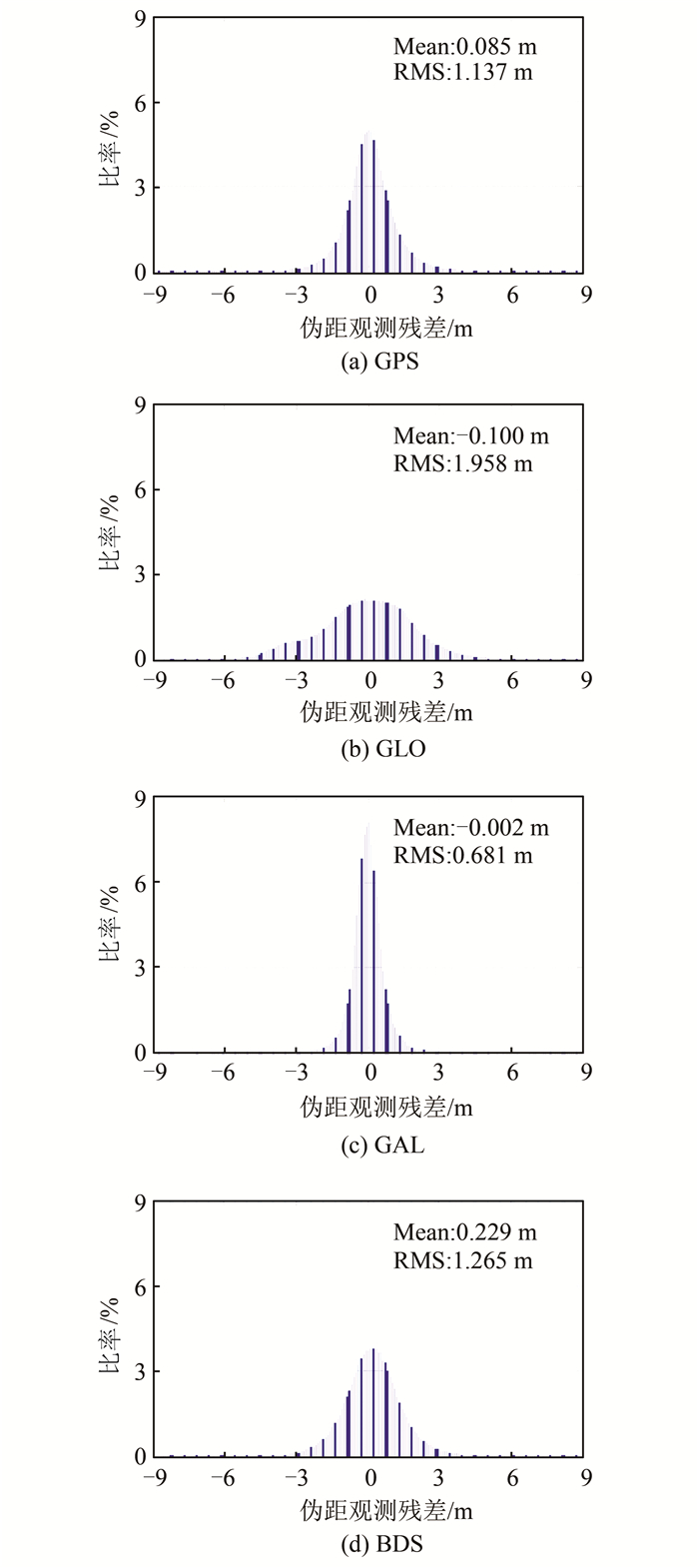 |
| 图 5 静态模式下四系统组合实时PPP伪距观测残差的分布 Fig.5 Distribution of Code Observation Residuals for Four-Constellation Integrated Real-Time PPP in the Static Mode |
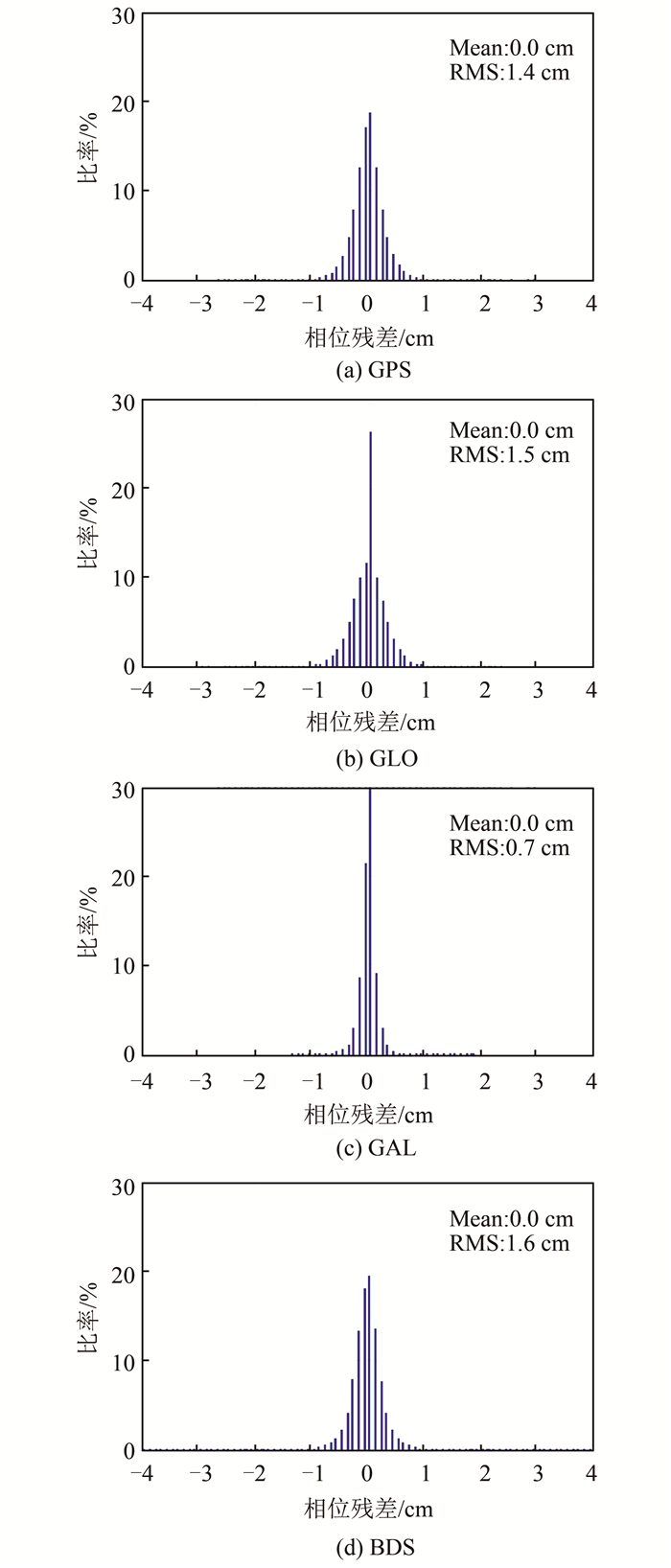 |
| 图 6 静态模式下四系统组合实时PPP相位观测残差的分布 Fig.6 Distribution of Phase Observation Residuals for Four-Constellation Integrated Real-Time PPP in the Static Mode |
3 结束语
本文对CNES RTS产品中不同星座的实时精密卫星轨道和钟差改正值精度进行了评估,为四系统组合实时PPP随机模型的确定提供了参考。评估了四系统组合实时PPP静态和动态定位性能。在静态模式下,与GPS单系统实时PPP相比,四系统组合实时PPP的收敛时间在东、北、高3个方向改善了43%、19%、26%;定位精度在3个方向改善了16%、25%、10%;单日收敛精度在3个方向分别为11.7 mm、8.0 mm、13.0 mm。动态模式下,相应的收敛时间改善为61%、35%、51%,相应的精度改善为29%、30%、21%,四系统组合实时PPP收敛后3个方向的定位精度分别为22.5 mm、18.8 mm、40.6 mm。对四系统组合实时PPP伪距和相位观测残差进行分析,4个卫星系统的观测残差均在可接受范围内,表明各种误差和偏差在四系统组合实时PPP模型中得到了很好的处理。
| [1] |
Pan L, Zhang X, Li X, et al. Satellite Availability and Point Positioning Accuracy Evaluation on a Global Scale for Integration of GPS, GLONASS, BeiDou and Galileo[J]. Advances in Space Research, 2017, 63(9): 2 696-2 710. |
| [2] |
Cai C, Gao Y, Pan L, et al. Precise Point Positioning with Quad-Constellations: GPS, BeiDou, GLONASS and Galileo[J]. Advances in Space Research, 2015, 56(1): 133-143. DOI:10.1016/j.asr.2015.04.001 |
| [3] |
Pan L, Zhang X, Liu J, et al. Performance Evaluation of Single-Frequency Precise Point Positioning with GPS, GLONASS, BeiDou and Galileo[J]. Journal of Navigation, 2017, 70(3): 465-482. DOI:10.1017/S0373463316000771 |
| [4] |
Li X, Ge M, Dai X, et al. Accuracy and Reliability of Multi-GNSS Real-Time Precise Positioning: GPS, GLONASS, BeiDou and Galileo[J]. Journal of Geodesy, 2015, 89(6): 607-635. DOI:10.1007/s00190-015-0802-8 |
| [5] |
Li P, Zhang X. Integrating GPS and GLONASS to Accelerate Convergence and Initialization Times of Precise Point Positioning[J]. GPS Solutions, 2014, 18(3): 461-471. DOI:10.1007/s10291-013-0345-5 |
| [6] |
Li X, Zhang X, Ren X, et al. Precise Positioning with Current Multi-Constellation Global Navigation Satellite Systems: GPS, GLONASS, Galileo and BeiDou[J]. Scientific Reports, 2015, 5: 8328. DOI:10.1038/srep08328 |
| [7] |
徐绍铨, 张永军, 李振洪, 等. GPS/GLONASS组合定位系统的精度分析[J]. 测绘信息与工程, 2000, 25(1): 22-25. DOI:10.3969/j.issn.1007-3817.2000.01.007 |
| [8] |
于兴旺, 张小红, 邰贺, 等. GPS/GLONASS组合单点定位在导航中的应用[J]. 测绘信息与工程, 2007, 32(6): 1-3. DOI:10.3969/j.issn.1007-3817.2007.06.001 |
| [9] |
匡团结, 王兵海. 基于PPP的动对动定位技术与精度分析[J]. 测绘信息与工程, 2009, 34(1): 14-15. |
| [10] |
Zhang L, Yang H, Gao Y, et al. Evaluation and Analysis of Real-Time Precise Orbits and Clocks Products from Different IGS Analysis Centers[J]. Advances in Space Research, 2018, 61(12): 2 942-2 954. DOI:10.1016/j.asr.2018.03.029 |
| [11] |
Wang L, Li Z, Ge M, et al. Validation and Assessment of Multi-GNSS Real-Time Precise point Positioning in Simulated Kinematic Mode Using IGS Real-Time Service[J]. Remote Sensing, 2018, 10(2): 337. DOI:10.3390/rs10020337 |
 2020, Vol. 45
2020, Vol. 45

