| 新型地铁轨道控制网复测精度控制指标分析 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室, 湖北 武汉, 430079;
3. 陕西省测绘地理信息局,陕西 西安,710054
2. Key Laboratory of Precise Engineering and Industry Surveying, National Administration of Surveying, Mapping and Geoinformation, Wuhan 430079, China;
3. Shanxi Administration of Surveying, Mapping and Geoinformation, Xi'an 710054, China
地铁轨道铺设是否平顺直接关系到地铁运行的安全、平稳、舒适,传统的地铁铺轨通常是根据隧道内布设的基标点进行的。控制基标通常采用精密导线的方式测量,但是导线测量多余观测少,可靠性不高,加密点相对精度较低,因此,越来越多的城市在布设地铁轨道控制网时引入高铁CPⅢ测量技术。受地铁隧道小半径曲线较多、隧道壁遮挡、地铁列车速度运行较慢、上级控制点精度较低等因素的影响,地铁轨道新型控制网的布设、观测方式与高铁CPⅢ控制网的略有不同。一般情况下,地铁轨道新型控制网的控制点弯道部分纵向间距为26 m左右,直线段为40 m左右。观测时,采用自由设站边角后方交会网进行测量,每一站观测测站前后各两对,一共4对控制点,搬站的距离为一对控制点的距离,相邻的两站重复观测6个控制点。
地铁轨道控制网的网点会受到二期荷载、基础的稳定性、施工干扰及一些人为破坏等因素的影响,其点位可能发生变化,所以铺轨在使用前必须对地铁轨道控制网进行复测,以确保其精度和可靠性[1-4]。同时,在施工单位完成施测的地铁轨道控制网,也必须由代表业主的地铁测量单位进行复测认可,才能进行下一步的铺轨测量。对地铁轨道控制网的复测直接参照CPⅢ平面网控制指标,或酌情降低一些,目前还没有合理的规定。本文在文献[1]的基础上,推导合理的地铁轨道控制网复测控制指标。同时,因地铁轨道控制网的复测与施测不是同一个单位,使用仪器设备的精度也不一样,特别是测距误差中,由于仪器检定机构的检定精度各不相同,在采用检定的加、乘常数对不同仪器的距离进行改正时,往往存在系统性偏差。本文通过模拟计算的方式,探讨测距偏差对地铁轨道控制网复测的影响[5-12]。
1 合理复测精度控制指标推导新型地铁轨道控制网在平差计算时,采用的计算模型与高铁CPⅢ控制网的完全一致,精度评定的指标体系也是一致的。由于地铁工程测量中使用该新型轨道控制网尚在前期实验阶段,地铁线路与高铁不同,测量成果往往达不到高铁规定的要求,地铁的运行速度也远远低于高铁,其轨道控制网也不需要达到高铁CPⅢ的精度,为此专门进行了模拟计算分析,综合考虑了测角、测距误差及网形分布等影响因素,经分析试算认为[1]:① 每1 000 m左右在车站处联测一个上级控制点的地铁轨道控制网,最弱点点位中误差应优于±5 mm,每600 m左右联测的应优于±3 mm;② 地铁轨道控制网的相邻点相对中误差指标可定为优于±1 mm。地铁轨道控制网同一控制点复测与原测的X、Y坐标较差分别为:
| $ \left\{ \begin{array}{l} \Delta X = {X_2} - {X_1}\\ \Delta Y = {Y_2} - {Y_1} \end{array} \right. $ | (1) |
式中,下标1、2分别表示原测、复测的成果。对式 (1) 运用误差传播律,得到复测与原测坐标较差的中误差为:
| $ \left\{ \begin{array}{l} m_{\Delta X}^2 = m_{{X_2}}^2 + m_{{X_1}}^2\\ m_{\Delta Y}^2 = m_{{Y_2}}^2 + m_{{Y_2}}^2 \end{array} \right. $ | (2) |
式中,m2Xi=σ2QXiXi;m2Yi=σ2QYiYi(i=1, 2)。其中,σ是后验单位权中误差;QXiXi和QYiYi分别为X和Y的协因数。
地铁轨道控制网的平面上级控制点的间距约为1 000 m时,约束平差后的点位中误差为5 mm,即mP=
由于地铁轨道控制网的平面网复测与原测的网形大体一致,采用同一平面上级控制点决定的平面基准、复测精度评价指标与原测的大小相同,为:
| $ \left\{ \begin{array}{l} {m_{\Delta X}} = \sqrt {m_{{X_2}}^2 + m_{{X_1}}^2} = 5{\rm{mm}}\\ {m_{\Delta Y}} = \sqrt {m_{{Y_2}}^2 + m_{{Y_2}}^2} = 5{\rm{mm}} \end{array} \right. $ | (3) |
取两倍中误差作为限差,则地铁轨道控制网的平面上级控制点的间距约1 000 m时,同一控制点复测与原测的X、Y坐标较差的限差为10 mm。同理,地铁轨道控制网的平面上级控制点的间距约600 m时,同一控制点复测与原测的X、Y坐标较差的限差为6 mm。
对于相邻点坐标增量较差,地铁轨道控制网相邻两点A(XA,YA) 和B(XB,YB) 的复测与原测的坐标增量较差为:
| $ \left\{ \begin{array}{l} \Delta {X_{AB}} = {\left( {{X_B} - {X_A}} \right)_2} - {\left( {{X_B} - {X_A}} \right)_1} = \\ \;\;\;\;\;\;\;\;\;\;\;\Delta {X_{AB2}} - \Delta {X_{AB1}}\\ \Delta {Y_{AB}} = {\rm{ }}{\left( {{Y_B} - {Y_A}} \right)_2} - {\left( {{Y_B} - {Y_A}} \right)_1} = \\ \;\;\;\;\;\;\;\;\;\;\;\Delta {Y_{AB2}} - \Delta {Y_{AB1}} \end{array} \right. $ | (4) |
对式 (4) 运用误差传播律,得到复测与原测坐标增量较差的中误差为:
| $ \left\{ \begin{array}{l} m_{\Delta {X_{AB}}}^2 = m_{\Delta {X_{AB2}}}^2 + m_{\Delta {X_{AB1}}}^2\\ m_{\Delta {Y_{AB}}}^2 = m_{\Delta {Y_{AB2}}}^2 + m_{\Delta {Y_{AB1}}}^2 \end{array} \right. $ | (5) |
式中,m2ΔXABi=σ2QΔXiΔXi;m2ΔYABi=σ2QΔYiΔYi(i=1, 2),各字母含义与网中相邻点相对中误差含义相同。
地铁轨道控制网的平面网约束平差后的相邻点相对中误差为1 mm,而相邻点相对中误差含X、Y两个坐标中误差分量,按等影响原则考虑,mΔXABi=mΔYABi=1/
| $ \left\{ \begin{array}{l} {m_{\Delta {X_{AB}}}} = {\rm{ }}\sqrt {m_{\Delta {X_{AB2}}}^2 + m_{\Delta {X_{AB1}}}^2} = 1{\rm{mm}}\\ {m_{\Delta {Y_{AB}}}} = {\rm{ }}\sqrt {m_{\Delta {Y_{AB2}}}^2 + m_{\Delta {Y_{AB1}}}^2} = 1{\rm{mm}} \end{array} \right. $ | (6) |
取两倍中误差作为限差,则地铁轨道控制网复测和原测的相邻点坐标增量较差的限差为2 mm。
2 模拟计算验证本文采用模拟轨道控制网的方法进行分析计算。首先,使用AutoCAD软件设计出不同情况的网型;其次,根据设计点的坐标和测站观测关系反算出测站到观测点的距离和水平方向观测值;再次,在观测值上根据仪器的标称精度加上相应的随机误差即可得到模拟控制网的观测值,对多期模拟出的观测值进行Helmert方差分量估计平差计算;最后,作多期比较分析。
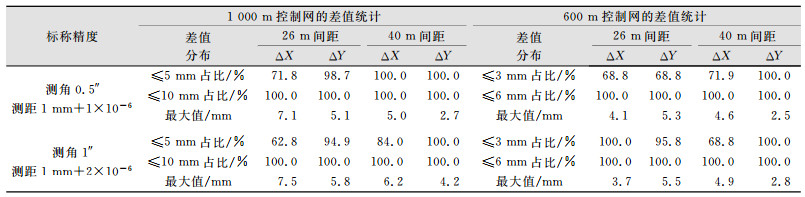
为了验证推导出的复测精度控制指标,采用测角精度为0.5″、测距精度为1 mm+1×10-6和测角精度为1″、测距精度为1 mm+2×10-6两种精度组合,按1 000 m和600 m两个长度,采用模拟直线形式的地铁隧道。考虑到地铁隧道中控制网的最短纵向间隔约为26 m,一般间隔约40 m,点对纵向按26 m、40 m两种间距进行模拟计算。计算统计结果如表 1和表 2所示。
| 表 1 坐标差值统计 Table 1 Difference Statistics of the Coordinates |
 |
| 表 2 相邻点坐标增量差值统计 Table 2 Statistics of the Coordinate Increments Difference Between Neighbor Points |
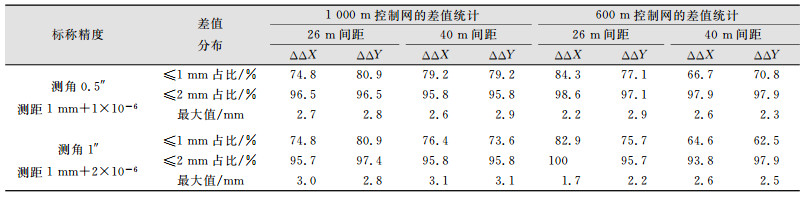 |
从表 1、表 2可以看出,在观测中只考虑随机误差的情况下,对复测坐标差,当控制网约束长度约为600 m时,满足6 mm限差要求;当约束长度约为1 000 m时,满足10 mm限差要求,且与设定的限差比普遍偏小。对坐标增量较差,95%以上的点满足2 mm限差,与偶然误差落在2倍标准差之内的概率为95.4%理论值相符,但较差最大值约为3 mm。
3 测距改正常数偏差对复测控制指标的影响为分析测距改正常数偏差对地铁轨道控制网复测的影响,下面从加常数的偏差和乘常数的偏差两个方面进行模拟计算分析。
为分析测距改正常数偏差对复测控制指标的影响,原网观测值采用只考虑随机观测误差的正常方法模拟,复测网距离观测值中加入测距改正常数偏差值,其余观测值与原网采用相同的随机数进行模拟。
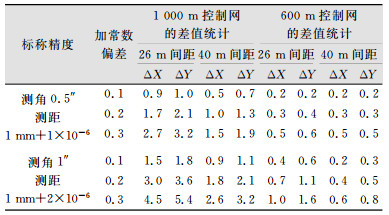
3.1 测距加常数偏差的影响考虑不同全站仪因仪器检定机构的检定精度不同,检定的加常数往往存在系统性偏差,其偏差值可能在0.1~0.3 mm之间。因此,在复测观测值的每条测距边上分别加上0.1 mm、0.2 mm和0.3 mm的偏差,将原网与复测网的结果进行比较,计算测点坐标差和相邻点坐标差较差,并统计了最大差值,结果如表 3和表 4所示。
| 表 3 坐标最大差值统计/mm Table 3 Maximum Difference Statistics of Coordinates/mm |
 |
| 表 4 相邻点坐标增量最大差值统计/mm Table 4 aximum Difference Statistics of Coordinate Increments Between Neighbor Points/mm |
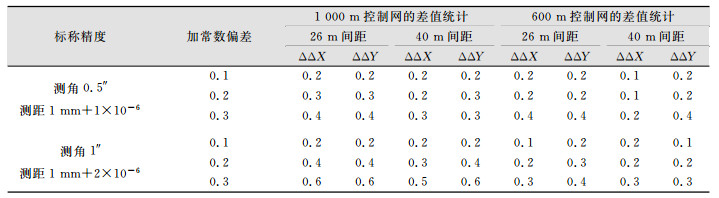 |
从表 3、表 4可知,长度较大的控制网,复测与原测坐标差值受加常数偏差的影响较大;点对纵向间距越小的控制网,复测与原测坐标差值受加常数偏差的影响越大;测角测距精度越差的控制网,复测与原测坐标差值受加常数偏差的影响越大。
对1 000 m的控制网,0.2 mm的加常数偏差最多可能导致3 mm左右的坐标差值,对600 m的控制网,只产生约1 mm左右的坐标差值。此部分的影响叠加到前面分析的坐标差值中,将使复测坐标差值更接近推导值。原测与复测的坐标增量较差受加常数偏差的影响较小,对0.2 mm的加常数偏差,最多可能导致0.4 mm左右的坐标增量较差。
3.2 测距乘常数偏差的影响全站仪检定的乘常数存在系统性偏差一般较小,但城市地铁控制网的投影面一般与地铁实际的高程面往往不一致,边长需要进行投影改正,投影改正的影响与边长乘常数的影响一致,10 m投影面高差将产生1.5×10-6的边长改正。为全面考察边长比例因子的影响,在复测观测值的每条测距边上分别加上0.5×10-6、1×10-6m和2×10-6的偏差,将原网与复测网的结果进行比较,计算测点坐标差和相邻点坐标差较差,并统计最大差值,结果如表 5所示。
| 表 5 坐标最大差值统计 Table 5 Statistics of the Max Difference of Coordinates |
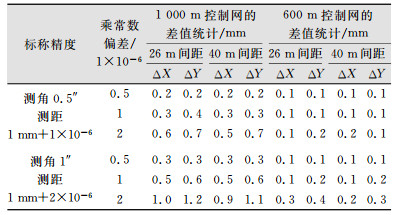 |
由表 5可以看出,测距乘常数偏差对控制网复测与原测坐标差值影响较小,2×10-6的偏差最大产生约1.2 mm左右差值。
测距乘常数偏差对相邻点的坐标增量差值影响很小,最不利的情况也不超过0.2 mm,其影响基本可以忽略。受篇幅限制,未将具体数据影响统计列出。
4 结束语通过以上的计算和分析可得出以下结论:
1) 综合考虑偶然误差及测距系统偏差的影响,地铁控制网的复测坐标差控制指标,对每1 000 m连测一个上级已知点的控制网可定为10 mm,对每600 m的控制网可定为6 mm。从坐标增量较差的模拟计算结果可看出,有约5%的较差超出了2 mm的限差,考虑地铁运营的速度远低于高铁,可适当放宽此项指标,地铁控制网的复测坐标增量较差控制指标可定为3 mm。
2) 地铁控制网复测时,距离观测值必须考虑加常数的改正,0.2 mm的加常数偏差,对每1 000 m连测一个上级已知点的控制网,其坐标差的影响可达约3 mm,对每600 m的控制网约为1 mm。
3) 测距乘常数偏差对地铁控制网复测坐标差及相邻点坐标增量差影响较小,但地铁控制网距离观测值需进行投影改正,应使原测与复测在同一个投影面上进行平差计算。
| [1] |
王忠仁. 地铁轨道控制网数据处理软件及精度评价指标研究[D]. 武汉: 武汉大学, 2016 |
| [2] | 徐秀川, 段双全, 宋超, 等. 影响地铁精密导线测距精度的因素及改正措施[J]. 测绘地理信息, 2015, 40(6): 35–37 |
| [3] | 武汉大学测绘学院测量平差学科组. 误差理论与测量平差基础[M]. 武汉: 武汉大学出版社, 2003 |
| [4] | 谯生有, 闻道荣. 无砟轨道CPⅢ平面控制网测量精度影响因素分析[J]. 测绘通报, 2011, (12): 47–49 |
| [5] | 尹观峰. 浅谈CPⅢ控制网程序对全站仪加常数的测定及分析[J]. 铁道勘测与设计, 2016, (1): 9–11 |
| [6] |
李建平. CPⅢ控制网精度控制及数据处理方法研究[D]. 武汉: 中国地质大学, 2013 |
| [7] |
中华人民共和国铁道部. TB 10601—2009. 高速铁路工程测量规范[S]. 北京: 中国铁道出版社, 2010 |
| [8] |
中华人民共和国住房和城乡建设部. GB 50157—2013. 地铁设计规范[S]. 北京: 中国建筑工业出版社, 2013 |
| [9] |
耿文燕. 无砟轨道CPⅢ控制网精算方法及数据处理研究[D]. 兰州: 兰州交通大学, 2014 |
| [10] | 于成浩, 柯明, 赵振堂. 精密工程测量中全站仪测距加常数的两种测定方法[J]. 测绘通报, 2007, (2): 55–57 |
| [11] | 王福学, 韩庆龙, 韩正阳. 浅析全站仪加常数、乘常数[J]. 测绘与空间地理信息, 2011, 34(2): 248–250 |
| [12] | 史晓萍, 朱庆峰. 非接触式自由设站隧道监控量测方法[J]. 测绘地理信息, 2015, 40(6): 79–81 |
 2017, Vol. 42
2017, Vol. 42

