| RTK无验潮水深测量误差分析及控制方法 | [PDF全文] |
2. 天津华北地质勘查局核工业二四七大队, 天津, 301800;
3. 陕西地矿第二综合物探大队, 陕西 西安, 710016;
4. 南京水利科学研究院, 江苏 南京, 210024
2. Tianjin Nuclear Exploration Bureau of North China Geological Exploration Bureau 247, Tianjin 301800, China;
3. The Second Group of Geology and Mineral Resources in Shaanxi Province, Xi'an 710016, China;
4. Nanjing Hydraulic Research Institute, Nanjing 210024, China
长期以来,为减小江河湖海不同位置处潮时差、潮比差等潮汐参数的影响,在水深测量时,需要同步设立适当的验潮站进行水位观测,然后对测深数据进行改正[1]。随着科学技术进步,全球导航卫星系统(global navigation satellite system,GNSS)的动态定位精度和稳定性逐渐提高,GNSS高精度垂直解已广泛应用于海洋测绘中[2],实时动态(real time kinematic,RTK)无验潮测深模式已成为海洋水深测量的发展方向并得到了大力推广,该方法已成为水深测量的技术方法之一,参考文献[3]中对无验潮测量作业的要求和限差给出了明确规定。与传统的有验潮测深相比,RTK无验潮水深测量具有全天候观测、实时快速测量、节省人工验潮成本、避免潮位观测误差、动态消除换能器吃水影响等诸多优势[4]。本文结合实践经验,围绕RTK无验潮水深测量原理及其影响因素进行分析探讨,提出了减小误差的控制方法。
1 无验潮水深测量原理及误差来源无验潮水深测量是利用载波相位差分技术RTK获取空间点位三维坐标(X,Y,Z)的优势,结合测深仪测量的水深数据,求得水下某点的三维坐标,历时不足1 s,平面和高程测量精度均可达cm级,完全能够满足海洋水深测量的要求。如图 1所示。
 |
| 图 1 无验潮水深测量原理 Fig.1 Principle of No-tide Measurement |
图 1中,h为换能器测量深度;h1为GPS天线高;h2为换能器吃水深度;H为海底泥面相对于深度基准面的标高;H1为GPS测量大地高;H2为GPS天线到深度基准面的距离;H3为深度基准面至参考椭球面的值。由图 1可以得出:
| $ H_{1}=H_{2}+H_{3} $ | (1) |
| $ H_{1}=h+h_{1}+h_{2}+H_{3}-H $ | (2) |
将式(1)代入式(2),海底泥面相对于理论深度基准面的标高为:
| $ H=h+h_{1}+h_{2}-H_{2} $ | (3) |
若将深度基准面当作似大地水准面,则H3即为高程异常ζ,式(2)可改写为:
| $ H=h+h_{1}+h_{2}-H_{1}+\zeta $ | (4) |
由式(3)、式(4)分析可以得出,RTK无验潮测深误差来源主要有三方面:一是由于不同测区的高程异常值ζ不同,且又无法准确测量某测点ζ值而引起的误差,即高程拟合的精度。由于拟合模型和方法不同,ζ值会产生一定的差异;二是因波浪引起的测量船纵横摇摆、上下沉浮、航向摆动,从而导致平面测量点的高程与实际测量高程不符而产生误差;三是GPS高程测量和换能器水深测量误差,若GPS天线和换能器的安装不垂直、GPS定位时刻与测深仪测深时刻不同步等会引起误差。
2 测深误差分析与控制 2.1 高程拟合误差不同的高程系统对应于不同基准面。我国常用的1985国家高程基准是以大地水准面为基准面。由于地球内部密度分布不均,大地水准面实际上是一个非常复杂的闭合曲面,难以精确计算,生产中若能求出高程异常值,即可求得正常高[5, 6]。高程拟合精度直接影响GPS所测得的大地高转换为正常高的质量。在不考虑GPS测量精度的前提下,高程拟合精度的影响主要来源于拟合模型采用的已经点精度和拟合转换方法。
选择正确模型是保证拟合精度的关键。模型选择需要考虑测区地形情况、数据收集情况等。常用的拟合模型可分为四类:线性拟合模型、平面拟合模型、地球重力场模型、地球重力模型与GPS水准相结合。拟合方法有加权平均法、线性移动拟合法、多项式拟合法、多面函数法等常规方法以及神经网络法和支持向量机法等,这些方法各有优缺点和适用范围[7]。通常在较平坦地区,采用多项式曲线拟合法和曲面拟合法,该法计算简单、易理解;在面积较大、地形较复杂的地区需要分区进行拟合,综合应用几种方法进行比较,选择一种拟合精度最优方法[8]。
实践证明,在已知点分布均匀、精度较高的情况下,根据测区条件及掌握的已知数据来选定正确的拟合模型,所求得的高程异常值精度可达到cm级。福建省似大地水准面的精化精度在平原地区为±5.6 cm,而在丘陵地区为±6.7 cm。福州市区域似大地水准面拟合模型转换高程与水准高程的较差最大为2.6 cm,利用网络RTK检核点精化高程与直接水准高程的较差小于5 cm[9]。我国西部地区,高程异常误差对坐标转换影响较大,达数厘米[10]。
在海洋RTK测量中,由于水准点无法覆盖海面区域,高程拟合通常采用外推的方法,离海岸越远误差影响越大。卢军明等[4]在辽宁某海域距海岸5 km、10 km、15 km、20 km进行有验潮与无验潮RTK水深测量试验,结果表明,在距海岸5 km、10 km、20 km处有验潮与RTK无验潮测量高程的较差分别为8 cm、22 cm、45 cm,足以满足近岸港口、航道水深测量要求。根据实践经验,在距海岸5 km以内的港口航道水深测量前,一般联测已知高程控制点3个以上;在距海岸5 km以上区域,通常需在海上建立临时验潮站进行改正。
2.2 测船姿态变化引起的误差在海洋测绘中,波浪引起测量船纵横摇摆和上下升降,对测深数据精度影响很大,波浪越大影响越大。测船的纵横摇摆使换能器辐射面的法线不能与水深基面保持垂直;测船的上下升降,使水深基面不断发生变化。当浪高0.7~1.0 m时,通常水深基面起伏达到10~40 cm;假设测量船的摇摆度为7°,在水深20 m处对中心波束的影响可达十几厘米,对边缘波束的影响会更大。测量船左右摇摆引起的误差如图 2所示。
 |
| 图 2 测船横摇误差 Fig.2 Ship Rolling Error |
假设天线与换能器完全在一条直线上,则水深测量的偏差Δh可表示为:
| $\Delta h=(L+H) \times(1-\cos \theta) $ | (5) |
式中,Δh为测船横摇引起的偏差;L为天线中心到换能器中心距离;H为换能器读数;θ为测船横摇角。式(5)即为测船横摇时的改正模型,纵摇模型与之类似。式中Δh≥0,表明波浪引起水深测量值恒大于实际水深,θ越大,Δh越大。根据本文推算,假设天线中心到换能器中心的距离L为5 m,在水深20 m处,当横摇角为7°、15°时,平面位置误差可达3.0 m、6.5 m,深度误差达0.2 m、0.9 m。
由波浪引起的测量船纵横摇、上下沉浮及航向摆动误差属于随机误差。通常在测船上安装姿态传感器测定测船姿态角进行改正,也可采用具有波浪自动补偿功能的测深仪。
2.3 RTK高程测量误差GPS-RTK测量误差主要与仪器标称精度、水准起算点精度、高程拟合精度、测站与基准站间的距离有关。从误差来源分析,主要有因卫星引起的误差、信号传播误差以及与接收机有关的误差。实际生产中通常会采用求差法、建立误差改正模型等进行消除或削弱。GPS高程测量精度通常采用内符合精度和外符合精度来衡量。目前常用的单频接收机在5 km范围内水平定位精度5 cm+1×10-6,双频接收机在50 km范围内的水平定位精度为5 cm+1×10-6,高程测量误差可近似按平面位置误差的2倍计算,比如南方灵锐S82-T RTK测量系统水平标称精度±(1 cm+1×10-6),垂直精度±(2 cm+2×10-6)。
实际生产中,为了消除电离层折射对观测值影响,通常采用双频接收机来保证精度,而且上午时段的观测精度普遍优于中午或下午的观测精度。
2.4 仪器安装不垂直的误差无验潮水深测量系统仪器安装误差主要为RTK天线、换能器安装的不垂直产生的误差。由于换能器杆连接了RTK天线和换能器,假设换能器杆安装不垂直,形成的偏角将导致换能器测量的水深值与平面位置不对应,产生系统误差。另外,由于RTK天线不垂直而使RTK测量高程比实际值偏小,也产生系统误差。
如图 3所示,仪器安装不垂直引起的误差为:
| $ \Delta h=(L+H) \times(1-\cos \alpha) $ | (6) |
 |
| 图 3 仪器安装不垂直误差 Fig.3 Vertical Error of Instrument Installation |
式中,L为天线中心到换能器中心距离;H为换能器测量值;α为换能器杆安装偏角;h为天线到海底的实际高度。
由式(6)可知,在换能器连接杆安装不垂直的情况下,测得的水深值比实际值要大,偏角越大,误差越大。假设换能器杆长2 m,水深30 m,偏角5°,则误差达到0.12 m。测量时常利用固定架将换能器杆固定在船舷中部平直处,安装后进行垂直度检查,或通过准确测量偏角,进行系统改正计算。
2.5 定位时延引起的位置偏移误差在无验潮测深中,测量点的平面位置由GPS-RTK获得,RTK一般在整秒时刻进行定位,其定位时刻与测深仪的标记时刻难以达到完全同步,船速越大延时误差亦越大。
如图 4所示,测量船按测线向东航行,在A0时刻,RTK进行测量船位置测量,获得B0点的位置坐标,而换能器发射声波信号滞后Δt,实际测量值为B1点处的水深值。若航速为v,则测深延时在航向上产生的位移量为L=v×Δt。
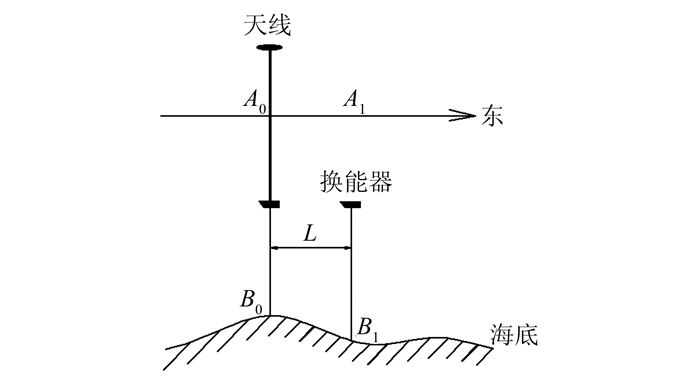 |
| 图 4 定位时延引起的位置偏移误差 Fig.4 Position Error by Location Delay |
若延迟为0.5 s,航速为10 km/h,将导致测量船偏离1~2 m。测量船以相反的方向航行时,在相邻测线测量点的水平相对误差成倍增加,造成等深线畸形,而且水下地形坡度越大误差越大。
实际工作中,由于RTK和测深仪的仪器型号不同,数据采样产生的延迟时间也不同,若时间差达到0.5 s,产生的误差将超过2~3 m,相邻测线测量点水平相对误差将达到2 m,不能满足1:1 000及以上大比例尺地图精度要求。
目前测量导航软件都具备实时改正的功能,一种方法是用户在测量前进行时间延迟测试,比如,利用水下凸起的岩石、管道线、尖角等特殊目标,使用波束的中心波穿越目标,求出一定航速下两者的时间关系,并在后续测量作业中船速尽量保持与测定的船速一致。若延迟值存在漂移情况,则此方法将不可用;另一种方法是时间同步法,利用GPS接收机输出频率为1 Hz的秒脉冲(1 PPS),连续调整测深系统处理单元的时间,使处理单元的时间始终与GPS时间保持同步[11],如SeaBat T50-P采集系统采用PPS时间同步,时间延迟非常小。
3 结束语本文通过对RTK无验潮测深原理和影响精度的5项主要误差进行定性定量分析, 可以得出以下结论。
1) RTK无验潮水深测量精度受高程异常影响大,在开放的海洋进行水深测量时,除了增加联测分布均匀的高程已知点、选择适当的拟合模型外,在距离海岸5 km以外较大区域测量时,还需增加临时潮位观测站进行改正。
2) 因波浪引起的船姿误差是影响水深测量精度的关键,但属于随机误差。测量前需关注天气、海浪的预报,当波浪过大时不宜进行测量。在波浪较小的情况下,可通过测定测量船姿态角进行改正,也可采用具有波浪补偿功能的测深仪。
3) 虽然GPS-RTK高程测量设备和技术能够满足海洋高程测量的要求,但测量前需对仪器进行检测,通常采用更高精度的双频接收机来保证测量精度。
4) GPS天线、换能器杆的安装误差及定位延迟误差属于系统误差。GPS天线、换能器杆的安装误差可以通过精确测量换能器连接杆的倾角进行改正;定位延迟误差可通过准确测定换能器的发射延迟时间进行改正,或采用PPS保持GPS时间与处理单元的时间一致。
对于海水声速引起的误差,通常在作业前使用剖面声速仪测定工作区附近海水各个深度层的实际声速值进行改正。
| [1] |
陆秀平, 边少峰, 黄辰虎, 等. 黄浦江航道多波束测深数据处理研究[J]. 海洋测绘, 2011, 31(3): 4-7. DOI:10.3969/j.issn.1671-3044.2011.03.002 |
| [2] |
赵建虎, 陆振波, 王爱学, 等. 海洋测绘技术发展现状[J]. 测绘地理信息, 2017, 42(6): 1-11. |
| [3] |
中华人民共和国交通运输部.水运工程测量规范: JTS 131-2012[S].北京: 人民交通出版社, 2012
|
| [4] |
卢军民, 安延云, 张东明, 等. 无验潮测深技术中影响水深测量精度的几个问题探讨[J]. 水运工程, 2010(5): 47-51. DOI:10.3969/j.issn.1002-4972.2010.05.010 |
| [5] |
陈安平, 李红伟. GPS高程拟合方法的比较研究[J]. 测绘地理信息, 2013, 38(3): 32-35. |
| [6] |
闫建伟, 周长江. GPS高程异常拟合研究及精度分析[J]. 全球定位系统, 2014, 39(1): 68-71. |
| [7] |
王继刚, 胡永辉. 三种综合高程异常的方法[J]. 测绘通报, 2009(4): 19-21. |
| [8] |
华锡生, 雷伟刚, 岳东杰. GPS高程异常模型的优选及分析[J]. 大坝观测与土工测试, 2000, 24(4): 16-18. DOI:10.3969/j.issn.1671-3893.2000.04.006 |
| [9] |
朱武松. 区域似大地水准面精化精度检测与应用验证—以福州市似大地水准面精化为例[J]. 福建建设科技, 2011(2): 68-70. DOI:10.3969/j.issn.1006-3943.2011.02.024 |
| [10] |
张勤, 王利. GPS坐标转换中高程异常误差影响规律研究[J]. 测绘通报, 2001(6): 12-14. DOI:10.3969/j.issn.0494-0911.2001.06.004 |
| [11] |
刘胜旋, 林勇, 黄辰虎. 1PPS时间同步对多波束测深质量的影响[J]. 海洋测绘, 2011(2): 31-33. DOI:10.3969/j.issn.1671-3044.2011.02.009 |
 2019, Vol. 44
2019, Vol. 44

