| 利用Leica TM30的储油罐变形监测技术研究 |
2. 武汉大学测绘学院,湖北 武汉,430079;
3. 海军工程大学导航工程系,湖北 武汉,430043
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China;
3. Department of Navigation, Naval University of Engineering, Wuhan 430033, China
能源战略储备是我国一项基本国策,特别在石油资源方面,对于应对能源危机、维护能源安全,具有重要意义。近年我国在沿海地区建设起大量石油储备基地,储油罐的建造也朝着大型化、密集型方向发展,其变形监测成为保障储油安全的重要工作[1]。最初的储油罐监测方法有围尺法、光学参比线法,其较高风险和强度使得难以适用于日益庞杂的工程对象[2, 3]。Leica TM30测量机器人具有稳定的罐体扫描程序,能自动识别、照准罐壁点,快速实现罐体和其他工程形变体的自动监测[4]。同时三维激光扫描技术和光栅光纤技术的发展,为油罐监测提供了新的技术手段,体现出巨大应用价值[5, 6]。
鉴于对储罐变形状态获取的准确、快速性,本文以Leica TM30为测量工具研究变形监测方法,在罐外测量方法基础上提出改进,以减少外业工作量。将整体最小二乘法应用于圈板圆心拟合,提高圆心拟合精度。结合工程实例,比较罐内测量结果,验证改进方法的精度和可靠性。
1 测量方法及实施立式储油罐一般采用钢制浮顶结构,罐壁由数块钢板焊接而成,厚度从上到下依次增加。由于设计、施工不当或受长期运营影响,储油罐会发生几何变形,其变形监测实质就是将各层圈板按1/4、3/4高度划分为各个监测层,对比其与基准圆相对位置关系分析变形情况。根据测量环境和条件,将储油罐监测方法分为罐内测量和罐外测量,其示意图如图 1所示[7]。
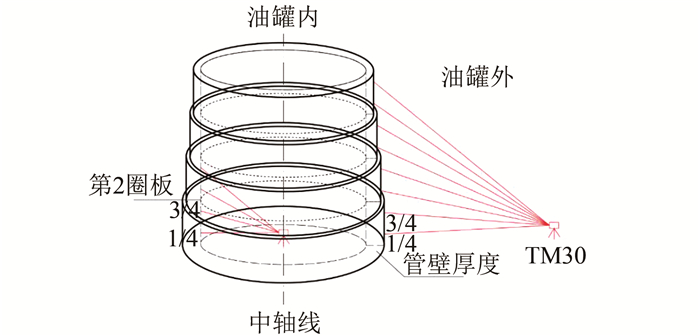 |
| 图 1 油罐检测示意图 Fig.1 Schematic Diagram of Oil Tank Detection |
罐外测量相对于罐内测量设站灵活,受油罐运行条件限制小,而被广泛应用,观测步骤如下:
1) 根据底圈板的设计内径和厚度,计算周长,选择1/4或3/4高度处作为基准圆,正北向为起始,顺时针均匀布设48个基圆标准点,建立形变分析基准。
2) 考虑罐外场地情况和基圆标准点位置,在罐外建立控制网,尽量少地布设控制点,使架设TM30能照准全部基圆标准点,罐外控制点坐标可由TM30内置导线测量程序实时计算。
3) 以48个基圆点沿储罐竖直方向建立48条母线,本文提出的改进方法就是直接在罐外控制点上(而非各条母线的径向上)架设TM30,测量基圆点坐标的同时,利用仪器基线扫描程序,自动测出各条母线方向上测站到各圈板1/4、3/4点处的平距。
传统测量方法是先在罐外控制点上架设仪器,测量出基圆点坐标,然后寻找各条母线径向方向重新架设仪器测量平距,最多时需再重新架站48次。改进后,罐外控制点个数决定了仪器架站次数,极大减少了外业工作量。
2 圆心拟合方法研究为充分研究罐体变形特征,需要对储油罐基圆点和各圈板进行圆心拟合,准确求出圆心位置是评估储罐变形的关键。考虑到测点坐标受到仪器精度的影响,不可避免地带有点位误差,利用最小二乘原理(least squares,LS)建立观测方程进行解算时,只考虑到点位误差对观测向量的影响,本文拟采用整体最小二乘法(total least squares method,TLSM)拟合圆心,并实验验证精度情况。
圆曲线方程可以表示为:
| $ {x^2} + ax + {y^2} + by + c = 0 $ | (1) |
构成观测方程:
| $ \mathit{\boldsymbol{L}} = \mathit{\boldsymbol{AX}} $ | (2) |
其中,
利用误差方程V = AX - L,可得最小二乘解
| $ \mathit{\boldsymbol{L}} + {\mathit{\boldsymbol{E}}_{\mathit{\boldsymbol{L}}}} = (\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{E}}_{\mathit{\boldsymbol{A}}}})\mathit{\boldsymbol{X}} $ | (3) |
整体最小二乘解法一般有奇异值分解,为便于编程计算,考虑系数矩阵中含有常数项,本文采用混合整体最小二乘法迭代求解[8]。
根据TM30测量精度(免棱镜测距精度:2 mm+ 2×10-6;测角精度:0.5″),站点距离一般小于150 m,计算测点的点位误差优于2.33 mm。假定圆心坐标和半径,计算均匀分布在圆周上的48个散点坐标,随机生成符合正态分布的变量X~N(0, (2.33× 10-3)2)作为测点误差,与其叠加,模拟出实测坐标。计算拟合的圆心坐标、半径与真实值的偏差值,记为εc和εr,重复试验100次,统计量如表 1所示[9]。
| 表 1 基于TLSM拟合圆心的ε统计量/mm Tab.1 Statistics of ε Based on TLSM/mm |
 |
由表 1可知,利用TLSM得到的拟合坐标和半径偏差比测点中误差小几个量级,说明TLSM能有效削弱测点点位误差,其较小的偏差值对储油罐形变分析的影响也可忽略。于是将整体最小二乘法应用于拟合储油罐基准圆和各层圈板的圆心和半径。
3 形变参数的计算对储油罐安全性评价参数主要有罐壁径向偏差、圈板椭圆度以及罐体倾斜度,并且基础沉降也是一个重要的监测内容。以下详细推导储罐形变参数的计算公式。
3.1 径向偏差和椭圆度为获得储罐的形变指标,首先需利用测站到罐壁点的平距计算出罐壁点平面坐标,罐外测量示意图如图 2所示。
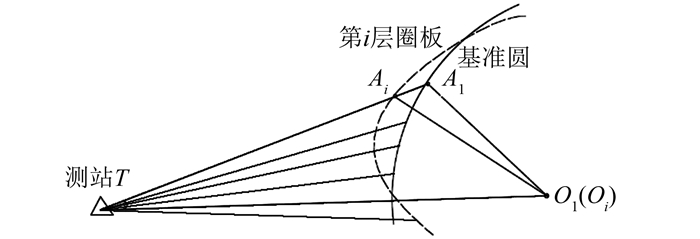 |
| 图 2 罐外测量示意图 Fig.2 Schematic Diagram of Outside Observation |
图 2中实线弧线代表基准圆,虚线曲线代表变形后第i层圈板,T为测站,O1、Oi为基准圆和第i层圈板的拟合圆心,A1、Ai分别为同一条母线上基圆点和第i层圈板测点。
罐壁点Ai平面坐标可由式(4)计算,z坐标由各层圈板高度确定。
| $ \left\{\begin{array}{l} x_{A}=x_{T}+D \cdot \cos \alpha \\ y_{A}=y_{T}+D \cdot \sin \alpha \end{array}\right. $ | (4) |
式中,(xT, yT)为测站T坐标;D为测站T到Ai平距;α为测线TAi方位角。
罐壁点Ai的径向偏差为:
| $ \sigma = {r_i} - r = \left( {{R_O}_{_i{A_i}} - {\varepsilon _i}} \right) - r $ | (5) |
式中,r、ri分别为基准圆拟合半径和罐壁点的内半径;εi为对应圈板实测厚度。
同一圈层48个测点对称排布,每相对两个点构成一条对向直径,则椭圆度计算公式为:
| $ \varphi=\left(d_{\max }-d_{\min }\right) / \bar{d} \times 100 \% $ | (6) |
式中,dmin、dmax和
每层圈板的倾斜度可由该层圈板1/4和3/4高度的拟合圆心Od(xd, yd, zd)、Ou(xu, yu, zu)确定,则圈板倾斜度v为:
| $ v=\operatorname{arctg} \frac{\sqrt{\Delta x^{2}+\Delta y^{2}}}{\Delta z} $ | (7) |
利用各圈层拟合圆心坐标Oi(xi, yi, zi),按空间直线最小二乘算法,计算罐体倾斜度V[10]:
| $ V=\operatorname{arctg} \sqrt{a^{2}+c^{2}} $ | (8) |
其中,
充分利用沉降数据,采用基础沉降差法对罐体倾斜结果进行验证,计算式为[11]:
| $ V=\operatorname{arctg}(\Delta s / L) $ | (9) |
式中,Δs为基础对径方向上最大沉降差;L为底圈板的外直径。
4 实例分析选取的监测对象为天津某输油站双浮顶金属储油罐,设计半径30 m,容积50 000 m3,罐壁设计高度为15.4 m,共由7层圈板焊接而成,每层圈板高度均为2.2 m。该储油罐建设年代久远并长期使用,受到地基沉降、风力等影响,可能发生变形,需对其进行变形监测。
检测时,储油罐处于腾空状态,罐内环境安全,并且罐外无遮挡,便于罐内和改进的罐外测量两种方法的实施。由于罐内测量精度高,将改进的罐外观测结果与罐内测量结果比较,以检验改进方法的精度和正确性。选取底圈板1/4高度作为基准圆,对比罐内外测量相同母线的径向偏差,如图 3所示,各圈板椭圆度和倾斜度数据对比如表 2、表 3所示。
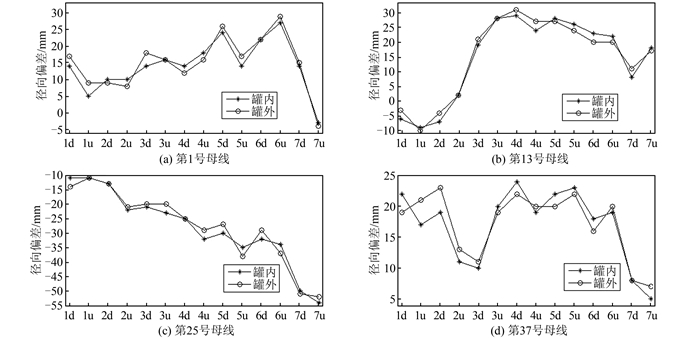 |
| 图 3 相同母线的径向偏差对比 Fig.3 Comparison of Radial Deviation of the Same Base Lines |
| 表 2 各圈层椭圆度对比/% Tab.2 Comparison of the Ellipticity of Each Ring/% |
 |
| 表 3 各层圈板倾斜度对比/(°) Tab.3 Comparison of the Inclination of Each Ring/(°) |
 |
结合图 3、表 2和表 3,对比罐内外测量储油罐形变指标:罐体对称方向的母线径向偏差,差值最大为±5 mm;各层圈板的椭圆度和倾斜度差值范围分别为-0.022%~0.019%和-0.048°~0.036°。综合分析,各个形变指标都具有较小偏差,变化趋势一致,说明改进罐外观测方法达到罐内测量要求,能满足实际工程需要。
依据储油罐检定规程(JJG-168-2005),以罐内测量计算结果,分析该储罐变形情况:
1) 储罐底圈板径向偏差在-3~18 mm内,其余各圈板最大值为48 mm,最小值为-54mm,较大偏差出现在中上层圈板,变形值均小于规定的±19 mm和±57 mm。底圈板与罐基础焊接,板壁厚度较大,具有很强约束,并且油罐长期处于高液位状态,中上部受油压影响大,所以罐体呈现下层位置变形小,中上部变形大的状态。结合图 3发现,第25号母线位置附近具有较大内凹变形,分析该位置为进出油口,受到各种力的作用大,出现了较大变形。
2) 由表 2可得,各层圈板椭圆度具有从下至上逐渐增大的趋势,位于0.137%~0.230%范围内,小于规定值1%。中上部位置较大的横向变形也是由于长期高液位油压造成。
3) 由表 3可得,各层圈板上层较于下层具有更大倾斜变形,位于0.042°~0.253°范围内,远小于规定值1°。综合考虑,该变形情况的出现是由于上层圈板受到焊接约束力小、油压作用大,并且该罐位于沿海地区,上层受到风力影响较下层也较大。整体倾斜度计算为0.026°,倾斜方向为西南方向,与基础最大沉降方向一致,利用最大沉降差计算倾斜度为0.035°,差值较小,验证了倾斜程度的正确性。
综上所述,该储油罐各个形变指标均小于规定值,变形程度小,整体处于安全状态。但上层圈板位置径向偏差较大,应适当对其进行加固与防护。
5 结束语为实现储油罐高精度、高效率的变形监测,本文详细阐述了基于Leica TM30的油罐变形监测方法,提出改进的罐外观测方法,即在控制点上架站,一次测得基圆点坐标和站点平距,可减少外业大量工作。将整体最小二乘法应用于拟合圆心,实验验证其能显著消除测点点位误差,具有较好的拟合精度。利用基础沉降差法验证了罐体倾斜度计算正确性,其能满足储油罐等简单形变体的倾斜观测。最后结合工程实例,验证了改进方法的精度和可靠性,该方法可以推广使用。
| [1] |
佟仕忠. 立式金属罐容量计量方法的研究[D]. 沈阳: 东北大学, 2012
|
| [2] |
张明. 10万m3立式油罐容积的标定与分析[J]. 油气储运, 1993(6): 43-46. |
| [3] |
Beshr E W. Structural Data Analysis for Monitoring the Deformation of Oil Storage Tanks Using Geodetic Techniques[J]. Journal of Surveying Engineering, 2014, 140(1): 44-51. DOI:10.1061/(ASCE)SU.1943-5428.0000120 |
| [4] |
李敬唐. TCA2003测量机器人高程测量精度研究[J]. 测绘地理信息, 2017, 42(4): 92-94. |
| [5] |
祁志江, 张柱柱, 焦光伟, 等. 基于三维激光扫描技术的油罐变形检测方法[J]. 油气储运, 2018, 37(1): 74-79. |
| [6] |
熊浩, 武应文. 光纤光栅感温探测系统在原油库的应用探析[J]. 科技创新导报, 2013(22): 48-49. DOI:10.3969/j.issn.1674-098X.2013.22.031 |
| [7] |
冯萌, 郭巍. 大型储罐几何形体变形检测方法的研究与应用[J]. 工程勘察, 2016, 44(6): 74-78. |
| [8] |
姚宜斌, 黄书华, 陈家君. 求解自回归模型参数的整体最小二乘新方法[J]. 武汉大学学报·信息科学版, 2014, 39(12): 1463-1466. |
| [9] |
田镇, 杨志强, 石震, 等. 一种曲线拟合圆心坐标算法及精度分析[J]. 测绘科学, 2016, 41(11): 31-34. |
| [10] |
史翔, 赵超英, 刘万科. 空间直线拟合的加权极坐标法[J]. 测绘地理信息, 2019, 44(2): 120-123. |
| [11] |
陈梦, 独知行, 张涛. 基于分区回归模型确定建筑物倾斜状态[J]. 测绘通报, 2019(3): 71-75. |
 2021, Vol. 46
2021, Vol. 46

