| 无线传感器网络变形监测研究综述 |
2. 精密工程与工业测量国家测绘地理信息局重点实验室,湖北 武汉,430079
2. Key Laboratory of Precise Engineering & Industry Surveying, NASG, Wuhan 430079, China
当前国内各种大型工程建筑物不断涌现,如桥梁、高塔及高层建筑等,它们在运营载荷、强风以及地震等外界因素的影响下都会产生振动与变形。变形过大将影响其正常运营,或使其产生局部性破坏乃至倒塌[1]。为了保证这些重大复杂工程结构在服务运营阶段的安全性,必须对其进行变形监测。GPS具有精度高、速度快、全天候、无需通视及自动化程度高等优点[2],但也存在着易受监测环境影响等缺点。地基雷达干涉测量虽能提供高精度的监测成果,但其设备成本昂贵。利用加速度仪、倾斜仪、自动跟踪全站仪等方法在高精度监测时存在局限性,不能满足大型工程建筑物自动、连续、实时动态监测的需求[3]。近年来出现的无线传感器网络技术[4]恰好能够弥补上述不足,通过布置在工程建筑物上的大量体积小的无线传感器节点动态采集其监测信息,摆脱线缆束缚,能够实现数据的无线多跳远距离传输,具有安装省时省力、组网方便、造价低廉等优点。
目前,国内外已经展开了基于无线传感器网络变形监测的相关研究[5-13]。 无线传感器网络变形监测研究分为数据获取与数据处理两部分,高效监测数据的可靠获取是进行数据处理分析的必要前提,通过对监测数据的处理能够及时掌握工程建筑物在服务运营阶段的健康状况,并对其安全性作出评估。无线传感器节点存在计算存储能力有限、能量有限及传输带宽有限等特点,欲实现其大规模应用仍存在一些需要解决的问题。本文主要分析无线传感器网络变形监测数据获取中的软硬件选取、时间同步、数据压缩及数据丢失等关键问题,同时论述振动监测数据的时域、频域以及模态域的数据处理方法,旨在推动无线传感器网络变形监测理论研究与工程实际应用的发展。
1 传感数据获取无线传感器网络变形监测的框架如图 1所示,其中数据获取是一个重要问题,只有获取可靠有效的监测数据才能保证数据处理的正常进行。鉴于传感器节点自身资源有限的特点,要想实现上述目的,从软硬件选择到数据采集乃至数据传输都存在着需要解决的关键问题。
 |
| 图 1 无线传感器网络变形监测框架 Figure 1 Wireless Sensor Networks Monitoring Framework |
1.1 软硬件选择
用于进行监测的传感器节点主要包括采集结构及环境信息的传感器和处理并发送这些信息的无线节点两部分。一般采集的主要是工程建筑物的振动信息,故常用的传感器为加速度计,当然经常也会使用应变计、风速计等传感器加以辅助。选取加速度计时,需从量程、灵敏度、噪声、采样率、模数转换分辨率及成本等方面综合考虑。
无线节点主要包括处理单元和通信单元等部分,作为处理单元的微控制器芯片集成了运算器、控制器、存储器、总线、输入输出等各种必要的功能,其特点是计算能力有限、功耗成本低,特别适合无线传感器网络的应用。目前常用于传感器节点的微控制器有MSP430系列、AVR系列及ARM系列等。通信单元的基本功能是将采集的监测数据以无线的方式传输到基站节点,当无法直接到达基站节点时,则需要中继节点进行转发,同时通信单元也负责接收由基站节点传输过来的控制命令。通信单元的选取主要从通信范围和能耗两个方面折中考虑,常用于无线节点的射频收发器有CC1000、CC2420、AT86RF230等。无线传感器节点一般采用电池供电,这使得节能问题成为无线传感器网络应用的重要议题,当前有研究利用环境振动发电或者太阳能来提供持续能量。几个典型的传感器网络结构监测案例所采用的节点包括Mica系列节点、Imote2节点以及Tmote-sky节点等。表 1展示了这些案例所采用节点的具体组成及其携带的传感器。
无线传感器网络的节点软件负责管理节点的传感器、射频以及电源等资源,为了降低开发难度,减少开发时间及成本,需采用嵌入式操作系统对底层硬件进行抽象,在操作系统的基础上开发应用程序。考虑到传感器网络的自适应性、健壮性及容错性和操作系统在不同硬件平台的可移植性,现有的嵌入式操作系统并不能满足无线传感器网络应用的要求,需结合其特点开发操作系统,对此,相关研究机构为无线传感器网络开发了TinyOS、Mantis OS、SOS及Contiki等操作系统[14]。
| 表 1 典型监测案例所采用的无线节点及其传感器 Table 1 Motes and Sensors in Typical Monitoring Cases |
 |
1.2 数据采集
对于诸如温度、湿度等环境监测任务,传感器节点的采样率非常低且数据量小,其大部分时间都处于休眠状态,而传感器网络下的变形监测任务通常则不同,为了实时掌握工程建筑物的变形情况,必须进行连续不断的高频采样。根据奈奎斯特采样定理,采样速率必须高于被采样信号所含最高频率的两倍之上才能精确重构原始信号,大多数工程建筑结构的基本频率为几Hz到几十Hz,设其基本频率为F,那么为了恢复工程建筑结构的振动信息,加速度计的采样率至少需达到2F。同时由于结构的高阻尼特性及降噪以提高信噪比的需要,需进一步提高采样率。以高斯白噪声σ为例,当将采样率提高到2NF时,噪声影响则会降低为
设一个采样单元的数据量为16 bit,当采样频率为1 000 Hz时,连续监测24 h,一个节点将产生约165 M的数据,如此大的数据量对资源有限的传感器节点来说是极其不利的,也给带宽有限的无线网络将数据汇聚到基站节点带来挑战,因此如何在不失真的情况下减少采样数据量是至关重要的。最近出现的压缩感知理论[15, 16]给大数据量的问题带来曙光,只要原始信号具有稀疏性或者可压缩性,传感器节点即可以远低于奈奎斯特采样率对信号进行非自适应线性投影,然后在终端采用相应的重构算法恢复原始信号。其理论思想为直接采集压缩的信号,简化采集端工作量,将复杂的信号重构交给终端处理,非常适合节点资源有限的传感器网络应用。不过目前该技术仍处于理论研究阶段,实际应用尚有距离。
数据采集中的时间抖动问题如图 2所示,分为节点内的时间抖动与节点间的时间抖动。节点内的时间抖动为高频采样条件下传感器节点无法保持等间隔采样。非等间隔采样误差将对数据处理带来影响,该问题主要由传感器节点软件系统引起,系统的任务抢占机制将影响采样任务的及时进行,即不可抢占任务将阻塞并延迟采样的进行。对于节点内部的时间抖动,需在分析其容许范围的基础上合理地设计节点软件程序,以保证采样任务的优先级,将抖动误差控制在数据处理容许的范围之内。节点间的时间抖动即为时间同步问题,由于每个节点都只维持自己的本地时钟,其开启时刻不同,接收到采集命令的时刻不同,导致节点开始采集的时刻不同而存在钟差,同时加上频偏及频漂的因素,会使得各节点之间的钟差越来越大。采集数据的节点间的时间紊乱会导致节点间的数据协同分析处理无法进行,因此必须周期性地对监测网络中的节点进行同步,将其统一在同一个时间基准之下。到目前为止,针对无线传感器网络已经提出了多种时间同步机制,如参考广播同步协议RBS[17]、无线传感器网络时间同步协议TPSN[18]、泛洪时间同步协议FTSP[19]等,在传感器网络动态监测中,Xu Ning等采用基于数据时间戳的同步技术,所有采集的数据在基站处同步,更多的研究人员主要采用现成的FTSP协议[20]。由于不同时间同步协议所考虑的实现复杂度、同步精度、能量效率等因素不同,现有的时间同步协议不一定完全适合无线传感器网络下工程建筑物变形监测的需求,需从数据采样率、数据处理所需的时间同步精度及节点时钟的稳定度等实际出发,结合现有的同步协议设计适合无线传感器网络变形监测的时间同步机制。
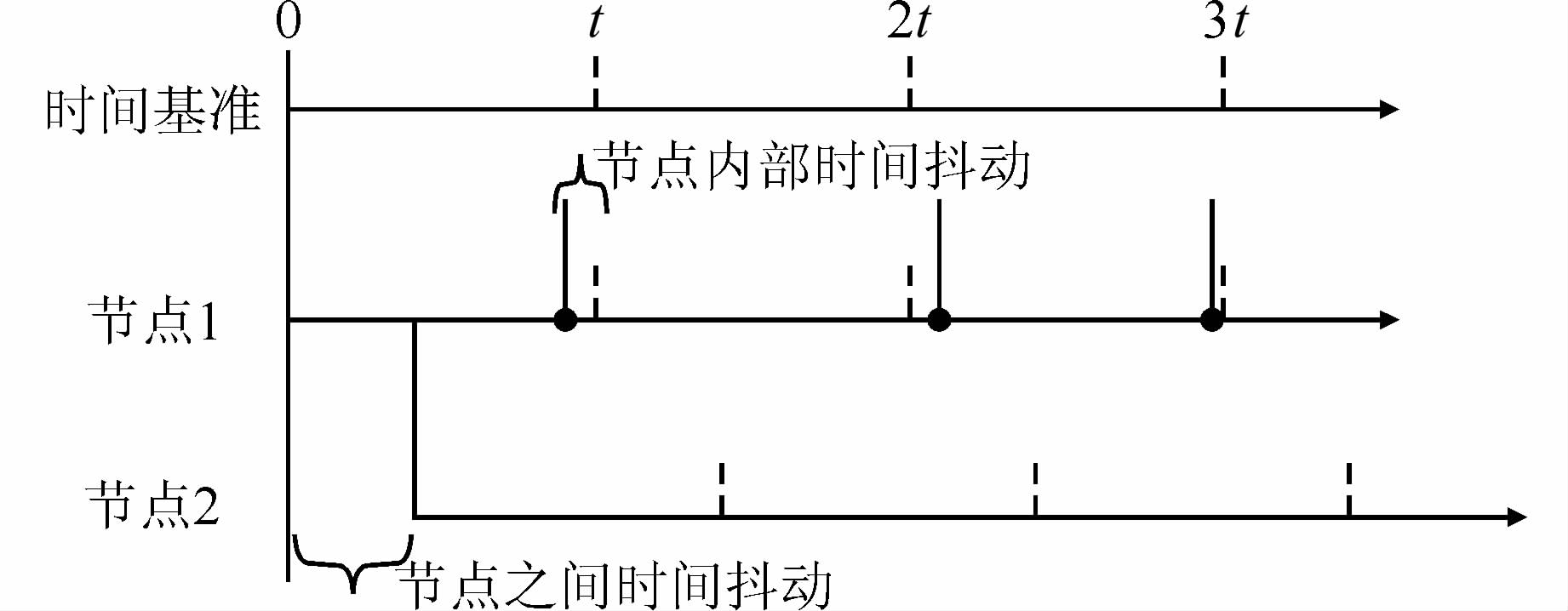 |
| 图 2 数据采集中的时间抖动 Figure 2 Time Jitter in Data Acquisition |
1.3 数据传输
传感器节点采集的原始监测数据需要传输到处理终端进行分析处理,然而其监测数据量大,无线传输带宽有限且易受干扰,此时数据压缩和数据丢失成为数据传输中的主要问题。
数据压缩主要是为减少存储空间,提高传输、存储及处理效率。根据压缩机制的可逆性与否,分为无损数据压缩和有损数据压缩。数据压缩在图像领域应用广泛,例如JPEG2000标准即采用了小波变换对原始图像进行压缩去除冗余数据[21]。在无线传感器网络变形监测中,为了获取有效的工程结构振动信息,必须进行高频采样,而高频采样将导致数据量大,这对传输带宽有限的无线传感器节点极为不利,因此必须在传输前对原始监测数据进行压缩处理[22-25]。对于传感器网络动态监测中数据压缩技术的性能评估,主要从压缩比、数据恢复误差、能量消耗、传输延迟及复杂度等方面来考虑。传感器节点采集的监测数据存在着相关性[26],那么利用传感器节点内部的时间相关性和传感器节点之间的空间相关性,在传统单节点压缩技术的基础上展开分布式K-L变换、分布式小波变换及分布式压缩感知等分布式数据压缩技术的研究在提高无线传感器网络变形监测中数据压缩的性能上具有重要意义[27]。
传感器节点采集的监测数据需要准确无误地传输到终端进行处理,不完整的数据将给数据处理带来困难。而无线传感器节点通信距离有限,远离基站的节点还需要通过其他节点进行多跳中继,且无线传输易受到环境的干扰而导致数据丢失。因此数据的可靠性也是数据传输中的重要问题,目前的研究主要从可靠传输协议设计与丢失数据恢复两个方面展开。
可靠传输协议设计包括传感器数据收集和控制命令分发两部分,协议需确保监测数据在多跳传输中万无一失地传输到数据处理终端,同时还需保证终端的控制命令毫无差错地分发到监测网络中的每个节点,使其都能够按照要求完成数据采集任务。数据传输协议主要包括丢失检测和丢失重传两个过程,无线传感器网络中常用的数据收集协议包括RMST、RBC、ESRT、PORT及STCP等[28],常用的控制命令分发协议包括PSFQ协议、GARUDA协议等。在无线传感器网络监测当中,Xu Ning等采用了跳到跳和端到端的两种模式对丢失的数据进行重传;Kim Sukun等则设计了Straw传输协议来保证监测数据在多跳传输过程中的可靠性;Nagayama设计了无线传感器网络监测中的可靠通信协议[29]。在设计无线传感器网络的可靠数据传输协议时,应综合考虑能量开销、缓存大小、复杂性及鲁棒性等问题。
针对传输过程中数据丢失问题的另一个解决方案即是在终端对丢失的数据进行恢复。通过分析数据处理技术中能够容忍的数据丢失率,允许监测数据在传输过程中存在丢失,然后在终端通过相应算法对丢失的数据进行恢复。常用的恢复技术为数据内插,鲍跃全等[30]则研究了利用压缩感知进行数据恢复的技术。数据恢复减少了数据重传率,节约了网络资源。
2 监测数据处理终端获取无线传感器网络传输过来的监测数据后需要及时处理,以掌握被监测工程建筑物的健康状况,当然也可以结合无线传感器节点的处理能力进行分布式数据处理。针对加速度监测数据,主要的数据处理方法包括时域、频域以及模态域分析。在数据处理之前,需要进行一些必要的预处理工作。
2.1 数据预处理加速度监测数据的预处理主要包括静动态测试、温度校正以及数据去噪等。静动态测试是为了对用于监测的加速度传感器进行检校,利用一台高精度的加速度计与被检校的加速度传感器分别在静态环境和动态环境下进行数据采集,通过对比来检测待检校传感器在静态环境中的偏移量以及对动态环境的响应情况。只有通过检校的加速度传感器才能用于工程建筑物的变形监测。
由于加速度传感器的敏感元件大多采用金属或者半导体材料,其采集的数据容易受到温度的影响,且监测环境的温度变化往往较大,导致加速度传感器的输出值存在偏差,因此需要配置温度传感器实时记录监测环境的温度信息来校正加速度传感器的输出值。通过记录加速度传感器的输出值、实际值以及温度信息,建立相应的数学模型,然后在数据采集程序中增加温度校正模块即可实现加速度输出值的自动校正,常用的温度校正模型为线性回归模型。
由于各种因素的影响,加速度数据在采集和无线传输过程中将不可避免地引入噪声,为了降低或消除噪声对数据分析的影响,必须对监测数据进行去噪预处理。针对振动数据常用的去噪技术包括中值滤波、卡尔曼滤波及Vondrak滤波等,同时小波分析及经验模态分解等技术也广泛应用于数据去噪中。对加速度监测数据经过去噪处理以后,即展开数据分析工作。
2.2 数据分析对于大型工程建筑物来说,振动监测数据分析即是以结构动力学为基础的模态参数识别,通过识别结构的固有频率、阻尼比和模态振型等参数为结构的健康评估提供依据。根据无线传感器网络获取数据的特点,一般采用全局的基于环境激励的模态参数识别方法,具体从时域、频率及模态域依次展开。
在时域上,有时需要将传感器节点采集的加速度振动信号转化为速度和位移信号。这主要通过积分处理来获取,设某节点采集的某方向的振动加速度信号为a(t),那么其速度信号为:
| $v(t)=\int\limits_{0}^{t}{a(t)d}t={v}'(t)+{{v}_{0}}$ | (1) |
位移信号为:
| $s(t)=\int\limits_{0}^{t}{v(t)}dt={s}'(t)+{{s}_{0}}$ | (2) |
在实际计算时,可以采用诸如梯形公式、辛普森公式等数值积分方法得到,同时需要解决加速度积分所带来的趋势项等问题。
针对获取的传感器节点的时域随机振动信号的另一个基本处理方法是计算相关函数。相关函数描述了随机振动信号在不同时刻瞬时值的关联程度,它包括自相关函数和互相关函数。自相关函数描述了某节点所采集的振动信号随时间变化的相互关联紧密性,互相关函数则描述了不同节点所采集的振动信号随时间变化的相互关联紧密性,其离散表达式分别如式(3) 、式(4) 所示:
| ${{R}_{xx}}\left( k \right)=\frac{1}{N}\sum\limits_{i=1}^{N-k}{x\left( i \right)x\left( i+k \right)},k=0,1,...,m$ | (3) |
| ${{R}_{xy}}\left( k \right)=\frac{1}{N-k}\sum\limits_{i=1}^{N-k}{x\left( i \right)y\left( i+k \right)},k=0,1,...,m$ | (4) |
式(3) 中,x(i)为某节点采集的离散振动信号;式(4) 中,x(i)、y(i)分别为不同传感器节点所采集的离散振动信号。
在频率上,主要的处理方法是以傅里叶变换为基础求得传感器节点所获取的随机振动信号的功率谱密度函数。它表示了信号的统计平均频谱特性,分为自功率谱密度函数和互功率谱密度函数。单个传感器节点采集的振动信号的功率谱密度函数称为自功率谱密度函数,它是该随机振动信号的自相关函数的傅里叶变换;两个不同传感器节点采集的随机振动信号的功率谱密度函数称为互功率谱密度函数,它为这两个信号的互相关函数的傅里叶变换,其离散表达式分别如式(5) 、式(6) 所示:
| ${{S}_{xx}}\left( k \right)=\frac{1}{N}\sum\limits_{r=0}^{N-1}{{{R}_{xx}}(r){{e}^{-{j2\pi kr}/{N}\;}}}$ | (5) |
| ${{S}_{xy}}\left( k \right)=\frac{1}{N}\sum\limits_{r=0}^{N-1}{{{R}_{xy}}(r){{e}^{-{j2\pi kr}/{N}\;}}}$ | (6) |
式中,Rxx(r)为某节点采集的信号的自相关函数;Rxy(r)为不同传感器节点采集的信号的互相关函数。
功率谱密度函数的估计分为非参数化方法和参数化方法。非参数化方法依据功率谱密度函数的基本定义进行估计,常用的方法包括周期图法、相关图法以及对它们进行的改进。参数化方法假设信号满足函数形式已知的参数模型,然后对假设模型中的参数进行估计。
模态域的分析即为模态参数的识别,基于环境激励的模态参数识别仅利用结构的响应数据来识别结构的模态参数,激励未知且通常假设为白噪声环境激励,根据数据的处理方式可分为时域法、频域法。
时域法直接利用传感器节点采集的振动监测数据进行模态参数的识别。常用的方法有时间序列法、随机减量法、NExT法、随机子空间法及模态函数分解法等。时间序列法利用随机过程和数理统计的理论对数据进行建模来识别模型参数,具体模型包括自回归模型、有外源的自回归模型、滑动平均模型、自回归滑动平均模型等,利用其进行参数识别的关键是确定模型的阶次。随机减量技术利用样本函数的期望值去掉响应数据的随机成分,从而得到加速度响应数据的自由振动响应,然后利用传统方法进行参数识别。NExT法的基本思想为结构两点之间响应的互相关函数与脉冲响应函数有相似的表达式,通过选取参考点计算采样数据的相关函数,然后再利用传统的模态参数识别方法进行识别。随机子空间法适用于平稳激励,它基于线性系统离散状态空间方程,通过计算状态空间方程的状态矩阵和输出矩阵实现模态参数的识别。模态函数分解法则是基于NExT法求得白噪声环境激励的响应后,对其进行模态函数分解得到各阶模态函数,然后通过Hilbert变换得到模态参数。
频域法模态参数识别主要包括峰值拾取法和频域分解法。由于无法获取结构的频响函数,峰值拾取法根据频响函数在固有频率附近出现峰值的原理,利用功率谱来代替频响函数进行模态参数识别。该方法识别误差较大,但操作简单,识别快。频域分解法是峰值拾取法的扩展,通过对响应的功率谱进行奇异值分解,将功率谱分解为对应多阶模态的一组单自由度系统功率谱,它克服了峰值拾取法的缺点,识别精度高,有一定的抗干扰能力。
3 结束语无线传感器网络技术的出现是以微机电系统(MEMS)、片上系统(SoC)以及无线通信和嵌入式技术等的飞速发展为基础的。它以其低功耗、低成本、分布式和自组织的特点为大型工程建筑物的变形监测提供了新的思路。然而由于无线传感器节点自身资源有限,在实际应用中仍存在一些需要解决的关键问题。在数据采集方面,恰当地选择软硬件能够在满足工程需求的同时降低成本,现有的研究案例为实际应用的选择做出了参考。高频采样带来的大数据量问题需要新的理论突破奈奎斯特采样定理来解决。节点内部及节点之间的时间抖动会影响采集数据的有效性,这需要结合现有的算法及变形监测要求来设计合理的机制。在数据传输方面,数据压缩是为了减少存储空间,提高传输效率,针对大量的监测数据,应利用无线传感器网络的特点展开分布式数据压缩的探索。数据的可靠性是数据分析处理的保障,可靠的传输协议设计与丢失数据恢复是数据可靠性的两个研究方向。在数据处理方面,首先通过预处理工作获取可用的振动监测数据,然后利用结构动力学的知识采用基于环境激励的模态参数识别方法进行模态参数的识别,为大型工程结构的健康评估提供依据。本文在数据采集、数据传输、数据处理等各方面进行了探讨,提出了解决方法。随着数据采集、数据传输以及数据处理中的问题逐步解决,基于无线传感器网络的大型工程建筑物变形监测技术将在国民生产建设中发挥巨大作用。
| [1] |
戴吾蛟, 伍锡锈, 罗飞雪. 高楼振动监测中的GPS与加速度计集成方法研究[J].
振动与冲击,2011,30(7) : 223–226.
Dai Wujiao, Wu Xixiu, Luo Feixue. Integration of GPS and Accelerometer for High Building Vibration Monitoring[J]. Journal of Vibration and Shock,2011,30(7) : 223–226. |
| [2] |
钟萍, 丁晓利, 郑大伟, 等. GPS结构振动监测数据滤波方法及其性能实验研究[J].
测绘学报,2007,36(1) : 31–36.
Zhong Ping, Ding Xiaoli, Zheng Dawei, et al. Filter-based GPS Structural Vibration Monitoring Methods and Comparison[J]. Acta Geodaetica et Cartographica Sinica,2007,36(1) : 31–36. |
| [3] |
匡翠林, 戴吾蛟. GPS监测高层建筑风致振动变形及小波应用[J].
武汉大学学报·信息科学版,2010,35(9) : 1024–1028.
Kuang Cuilin, Dai Wujiao. Measurement of Wind Induced Vibration of Tall Buildings Using GPS and Wavelet Application[J]. Geomatics and Information Science of Wuhan University,2010,35(9) : 1024–1028. |
| [4] |
任丰原, 黄海宁, 林闯. 无线传感器网络[J].
软件学报,2003,14(7) : 1282–1291.
Ren Fengyuan, Huang Haining, Lin Chuang. Wireless Sensor Networks[J]. Journal of Software,2003,14(7) : 1282–1291. |
| [5] | Jeongyeup P, Chintalapudi K, Govindan R, et al. A Wireless Sensor Network for Structural Health Monitoring: Performance and Experience[C]. The Second IEEE Workshop on Embedded Networked Sensors (EmNetS-II), Washington D C, USA, 2005 |
| [6] | Chintalapudi K, Fu T, Jeongyeup P, et al. Monitoring Civil Structures with a Wireless Sensor Network[J]. IEEE Internet Computing,2006,10(2) : 26–34. DOI:10.1109/MIC.2006.38 |
| [7] | Sukun K, Pakzad S, Culler D, et al. Health Monitoring of Civil Infrastructures Using Wireless Sensor Networks[C]. 6th International Symposium on Information Processing in Sensor Networks, IPSN, NY, USA, 2007 |
| [8] | Pakzad S N. Development and Deployment of Large Scale Wireless Sensor Network on a Long-span Bridge[J]. Smart Structures and Systems,2010,6(5/6) : 525–543. |
| [9] | Jang S, Jo H, Cho S, et al. Structural Health Monitoring of a Cable-stayed Bridge Using Smart Sensor Technology: Deployment and Evaluation[J]. Smart Structures and Systems,2010,6(5/6) : 439–459. |
| [10] | Rice J A, Mechitov K, Sim S H, et al. Flexible Smart Sensor Framework for Autonomous Structural Health Monitoring[J]. Smart Structures and Systems,2010,6(5/6) : 423–438. |
| [11] | Feltrin G, Meyer J, Bischoff R, et al. Long-term Monitoring of Cable Stays With a Wireless Sensor Network[J]. Structure and Infrastructure Engineering,2010,6(5) : 535–548. DOI:10.1080/15732470903068573 |
| [12] | Hu X Y, Wang B W, Ji H. A Wireless Sensor Network-Based Structural Health Monitoring System for Highway Bridges[J]. Computer–Aided Civil and Infrastructure Engineering,2013,28(3) : 193–209. DOI:10.1111/mice.2013.28.issue-3 |
| [13] | Xu N, Rangwala S, Chintalapudi K K, et al. A Wireless Sensor Network for Structural Monitoring[C]. The 2nd International Conference on Embedded Networked Sensor Systems, New York,USA, 2004 |
| [14] |
李晶, 王福豹, 段渭军, 等. 无线传感器网络节点操作系统研究[J].
计算机应用研究,2006,(8) : 28–30.
Li Jing, Wang Fubao, Duan Weijun, et al. Research on Node Operation System of Wireless Sensor Networks[J]. Application Research of Computers,2006,(8) : 28–30. |
| [15] | Candes E J, Wakin M B. An Introduction to Compressive Sampling[J]. IEEE Signal Processing Magazine,2008,25(2) : 21–30. DOI:10.1109/MSP.2007.914731 |
| [16] |
金坚, 谷源涛, 梅顺良. 压缩采样技术及其应用[J].
电子与信息学报,2010,32(2) : 470–475.
Jin Jian, Gu Yuantao, Mei Shunliang. An Introduction to Compressive Sampling and Its Applications[J]. Journal of Electronics & Information Technology,2010,32(2) : 470–475. |
| [17] | Elson J, Girod L, Estrin D. Fine-grained Network Time Synchronization Using Reference Broadcasts[J]. SIGOPS Operating Systems Review,2002,36(SI) : 147–163. DOI:10.1145/844128 |
| [18] | Ganeriwal S, Kumar R, Srivastava M B. Timing-sync Protocol for Sensor Networks[C]. The 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, California, USA, 2003 |
| [19] | Maróti M, Kusy B, Simon G, et al. The Flooding Time Synchronization Protocol[C]. The 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, 2004 |
| [20] | Nagayama T, Spencer B F, Rice J A. Autonomous Decentralized Structural Health Monitoring Using Smart Sensors[J]. Structural Control and Health Monitoring,2009,16(7/8) : 842–859. |
| [21] | Marcellin M W. JPEG2000: Image Compression Fundamentals, Standards, and Practice[M]. New York: Springer, 2002 . |
| [22] | Chintalapudi K K. Design of Wireless Sensor Network Based Structural Health Monitoring Systems[D]. Los Angeles :University of Southern California, 2006 |
| [23] | Lynch J P. An Overview of Wireless Structural Health Monitoring for Civil Structures[J]. Philosophical Transactions of the Royal Society, Series A: Mathematical, Physical and Engineering Sciences,2007,365(1851) : 345–372. DOI:10.1098/rsta.2006.1932 |
| [24] | Pakzad S N, Fenves G L, Kim S, et al. Design and Implementation of Scalable Wireless Sensor Network for Structural Monitoring[J]. Journal of Infrastructure Systems,2008,14(1) : 89–101. DOI:10.1061/(ASCE)1076-0342(2008)14:1(89) |
| [25] | Bao Y Q, Beck J L, Li H. Compressive Sampling for Accelerometer Signals in Structural Health Monitoring[J]. Structural Health Monitoring—An International Journal,2011,10(3) : 235–246. DOI:10.1177/1475921710373287 |
| [26] | Quer G, Masiero R, Pillonetto G, et al. Sensing, Compression, and Recovery for WSNs: Sparse Signal Modeling and Monitoring Framework[J]. IEEE Transactions on Wireless Communications,2012,11(10) : 3447–3461. DOI:10.1109/TWC.2012.081612.110612 |
| [27] | Duarte M F, Shen G, Ortega A, et al. Signal Compression in Wireless Sensor Networks[J]. Philosophical Transactions of the Royal Society, Series A: Mathematical, Physical and Engineering Sciences,2012,370(1958) : 118–135. DOI:10.1098/rsta.2011.0247 |
| [28] |
何庆伟, 孙利民, 刘俊涛. 无线传感器网络中的可靠传输研究[J].
计算机科学,2007,34(7) : 66–69.
He Qingwei, Sun Liming, Liu Juntao. Research on Reliable Transport in Wireless Sensor Network[J]. Computer Science,2007,34(7) : 66–69. |
| [29] | Nagayama T,Spencer B F. Structural Health Monitoring Using Smart Sensors[D].Urbana-Champaign:University of Illinois, 2007 |
| [30] | Bao Y Q, Li H, Sun X D, et al. Compressive Sampling-Based Data Loss Recovery for Wireless Sensor Networks Used in Civil Structural Health Monitoring[J]. Structural Health Monitoring,2013,12(1) : 78–95. DOI:10.1177/1475921712462936 |
 2016, Vol. 41
2016, Vol. 41

