| 利用北斗GEO卫星观测监测深圳市周围地区电离层空间环境 |
2. 武汉大学卫星导航定位技术研究中心,湖北武汉,430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
电离层延迟作为全球导航卫星系统(global navigation satellite system,GNSS)卫星信号传播过程中的一个重要误差源,严重影响卫星导航定位精度。近年来,众多学者在全球和区域电离层反演监测方面开展了许多工作,分析了全球和区域范围内的电离层时空变化特性[1, 2],并讨论了其与太阳和地磁活动周期性变化的相关性[3]。以上研究大多以地基GNSS等方式建立的全球或区域电离层模型为基础反演垂直方向电子总含量(vertical total electron content,VTEC),但在反演过程中又不可避免地引入误差,如国际GNSS服务(International GNSS Service,IGS)电离层工作组通过综合多家分析中心的电离层产品,按天发布时间分辨率为2 h的全球电离层模型(global ionosphere model,GIM)电离层格网产品,其精度为2~8 TECU[4]。北斗GEO卫星与其他轨道类型的卫星(如MEO卫星)相比,由于具有“静地特性”,在其服务的亚太中低纬度地区,在固定测站观测前提下可保持电离层穿刺点近似不变,因此可不引入电离层模型误差对电离层进行实时监测。
已有相关研究基于北斗GEO卫星数据,采用双频相位方法提取VTEC,并分析其在中国区域的全年变化特性[5]和磁暴期间的变化响应[6]。然而,相对于GNSS双频相位电离层VTEC的提取方法,非差非组合精密单点定位(precise point positioning,PPP)方法能够有效提高电离层延迟参数解算精度[7-10]。深圳市位于亚太低纬度地区,电离层复杂多变,本文利用深圳市部分监测站2020年的实测数据,采用非差非组合PPP反演获取北斗GEO卫星固定穿刺点位置的VTEC,将实测电离层VTEC与GIM产品进行对比,为了解该区域的电离层空间环境以及IGS提供的GIM电离层产品在该区域的表现提供参考。
1 估算VTEC的理论和方法 1.1 单站电离层延迟估计传统的PPP一般采用双频伪距/载波相位观测值通过线性组合在观测域上消去电离层延迟误差项,称为无电离层组合PPP算法。与传统PPP不同的是,非差非组合PPP不采用线性组合形式,而是将各站星之间的斜路径电离层延迟作为待估参数,并统一到同一频率,采用一定随机模型和参数估计方法,将其与测站位置接收机钟差和模糊度参数一起在滤波算法中同时估计[11],其原始基本观测方程如下:
| $ \left\{\begin{aligned} P_i=& \rho+c\left(\mathrm{~d} t_r-\mathrm{d} t^s\right)+\gamma_i I_1+T+\\ & c\left(d_{r, i}-d_i^s\right)+\varepsilon_p \\ L_i=& \rho+c\left(\mathrm{~d} t_r-\mathrm{d} t^s\right)-\gamma_i I_1+T+\\ & \lambda_i\left(N_i+b_{r, i}-b^{s, i}\right)+\varepsilon_l \end{aligned}\right. $ | (1) |
式中,P、L分别表示伪距和相位距离观测值;i表示频率号;ρ表示站星之间的真实几何距离;c表示光速;dtr和dts分别表示接收机钟差和卫星钟差;γi = f12/fi2,表示电离层转换系数,其中,f表示频率;I1表示第一频率的电离层延迟;T表示对流层误差;dr,i和dis分别表示非校正接收机端和卫星端伪距硬件延迟;br,i和bs,i分别表示非校正的接收机端和卫星端相位硬件延迟;λi和Ni分别表示对应频率波长和模糊度项;εp和εl分别表示伪距和相位观测中的测量噪声。
由于IGS基于无电离层组合方式发布精密轨道和钟差产品,其中,卫星钟差包含卫星伪距硬件延迟信息,其形式如下:
| $ \overline{\mathrm{d} t^s}=\mathrm{d} t^s+\frac{c f_1^2}{f_1^2-f_2^2} d_1^s-\frac{c f_2^2}{f_1^2-f_2^2} d_2^s $ | (2) |
令
| $ \left\{\begin{array}{l} P_i=\rho+c\left(\overline{\mathrm{d} t_r}-\overline{\mathrm{d} t^5}\right)+\gamma_i \overline{I_1}+T+\varepsilon_p \\ L_i=\rho+c\left(\overline{\mathrm{d} t_r}-\overline{\mathrm{d} t^5}\right)-\gamma_i \overline{I_1}+T+\overline{N_i}+\varepsilon_p \end{array}\right. $ | (3) |
式中,各参数表达如下:
| $ \left\{\begin{array}{l} \overline{\mathrm{d} t_r}=\mathrm{d} t_r+d_{r, \mathrm{IF}} \\ \overline{I_1}=I_1+\beta\left(D_r+D^s\right) \\ \overline{N_i}=\lambda_i\left(N_i+b_{r, i}-b^{s, i}\right)+c\left(d_{s, \mathrm{IF}}-d_{r, \mathrm{IF}}\right)+ \\ \quad \frac{c \gamma_i}{1-\gamma_2}\left(D_r+D^s\right) \\ d_{r, \mathrm{IF}}=\alpha d_{r, 1}+\beta d_{r, 2} \\ d_{s, \mathrm{IF}}=\alpha d_1^s+\beta d_2^s \end{array}\right. $ | (4) |
式中,
综上所述,本文采用卡尔曼滤波算法进行参数估计,随机模型采用卫星高度角定权,电离层延迟参数初值由双频伪距获得并作为随机游走参数进行估计,所估计的参数包括接收机位置参数、接收机钟差参数、模糊度参数、电离层延迟参数和对流层参数,其中,电离层延迟参数包含站星硬件延迟之和[7, 12]。
1.2 站星硬件延迟分离非差非组合PPP算法估计的电离层延迟包含站星硬件延迟之和项,其影响在±20 ns左右,且不同系统和频率间的卫星和接收机影响不同[13]。一般可通过事前标定或各机构发布的卫星端和接收机端DCB产品进行扣除,由于站星DCB在一天变化中比较稳定,在实际处理时通常将其当作常数与区域电离层模型系数一起估计,从而分离出绝对电离层延迟和站星DCB之和[13]。
硬件延迟的分离在电离层单层薄层假设下,将斜路径电子总含量(slant total electron content,STEC)通过投影函数转换至穿刺点天顶方向上的VTEC,本文采用的投影函数如下[14]:
| $ F(z)=\frac{S_T}{V_T}=\frac{1}{\sqrt{1-\left(\frac{R_e \cos Z}{R_e+H}\right)^2}} $ | (5) |
式中,ST表示STEC;VT表示VTEC;Re表示地球半径;Z表示卫星高度角;H表示电离层薄层高度,本文取450 km。对于单站地基电离层建模模型,一般采用多项式模型进行分时段建模[15],综合以上单站电离层模型,观测方程如下:
| $ B_s=\bar{I}_s-F(z) \sum\limits_{n=0}^N \sum\limits_{m=0}^M E_{n m}\left(\varphi-\varphi_0\right)^n\left(S-S_0\right)^m $ | (6) |
式中,Bs表示站星硬件延迟之和;Is表示非差非组合PPP估计的电离层延迟量;N和M表示模型最大阶数,本文均取2;Enm表示电离层多项式模型系数;φ和S分别表示穿刺点的纬度和太阳时角;φ0和S0分别表示建模中心点的纬度和中间时刻的太阳时角。基于上述观测模型,利用最小二乘估计算法可解算出时段对应的电离层模型系数和站星延迟量之和,实现电离层延迟量与站星DCB分离的目的。
2 数据处理和分析 2.1 北斗GEO卫星VTEC日解算精度为了评估非组合PPP算法解算北斗GEO卫星穿刺点VTEC的精度,利用相邻短基线测站观测北斗GEO卫星穿刺点位置近似固定且VTEC值近似相等的特性,本文选取了位于深圳市连续运行基准站(continuously operating reference station,CORS)系统中的两个观测站(A、B)2020年的数据,计算出在春分点、夏至点、秋分点和冬至点当日两个测站北斗GEO卫星穿刺点处的VTEC差值,并统计其日均值和标准差,由于C05卫星缺少部分观测数据,为保持数据完整性,本文仅统计C01~C04卫星,其穿刺点近似位置见表 1。
| 表 1 GEO卫星穿刺点的近似位置 Tab.1 Puncture Points 'Approximate Locations of GEO Satellite |
 |
图 1展示了相邻测站A、B解算的北斗GEO卫星VTEC差值。可以看出,由相邻测站A、B解算的北斗GEO卫星的VTEC符合性很好,各GEO卫星VTEC的差值统计结果如表 2所示。从单日解算统计结果来看,各GEO卫星的VTEC差值均值和标准差绝对值最大分别为0.26TECU和0.69TECU,这说明利用非组合PPP算法解算的北斗GEO卫星电离层穿刺点处的VTEC具有较高精度。
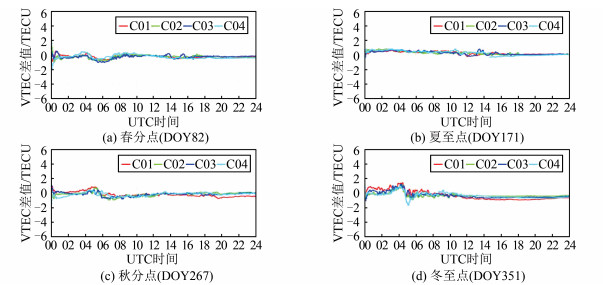 |
| 图 1 相邻测站A、B解算北斗GEO卫星VTEC差值 Fig.1 VTEC Differences of BeiDou GEO Satellite Calculated by Adjacent Stations A and B |
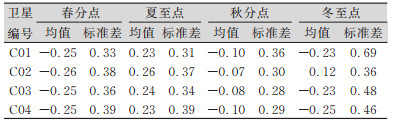
| 表 2 相邻测站A、B解算的北斗GEO卫星VTEC差值统计结果/TECU Tab.2 Statistics of VTEC Differences of BeiDou GEO Satellite Calculated by Adjacent Stations A and B/TECU |
 |
2.2 北斗GEO卫星电离层周年监测分析
根据上述分析中北斗GEO卫星VTEC的日解算精度,本文利用深圳市某测站2020年连续实测的北斗GEO卫星日解VTEC数据分析电离层的周年变化以及评估GIM电离层产品与实测值的差值精度。由于在固定测站前提下,北斗各GEO卫星穿刺点纬度差异很小,本文仅以C01卫星穿刺点位置反映该小区域纬度下的电离层变化。图 2是该穿刺点在2020年的VTEC实测日变化曲线,并由GIM内插出该穿刺点位置的VTEC值。
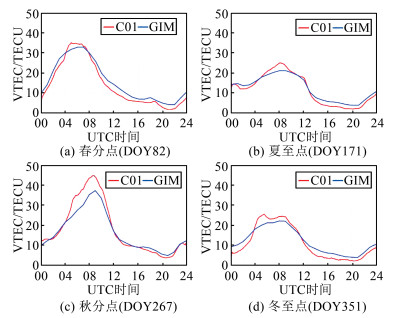 |
| 图 2 C01卫星在2020年各分至点的实测VTEC与GIM差异 Fig.2 Differences Between Measured VTEC and GIM VTEC of C01 Satellite at Equinoxes and Solstices in 2020 |
IGS每2 h提供一次全球电离层格网值,用户需要在空间和时间维度内插出对应时刻的VTEC值,相较于北斗GEO卫星固定位置实时监测,其连续性较差。由图 2可知,GIM内插值与实测C01卫星VTEC变化趋势基本一致,在春分点和秋分点处VTEC日幅整体大于夏至点和冬至点,体现出电离层的季节变化特性。上述实测VTEC与GIM内插值的差值(实测值-GIM内插值)如图 3所示,可见在该低纬度地区各分至点的VTEC差值均在日峰值时刻附近较大。
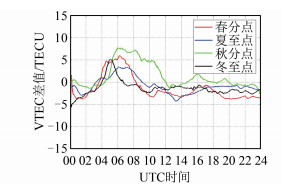 |
| 图 3 C01卫星在2020年各分至点的实测VTEC与GIM差异 Fig.3 Differences Between Measured VTEC and GIM VTEC of C01 Satellite at Equinoxes and Solstices in 2020 |
VTEC日峰值大小可反映当日电离层活跃水平,图 4为2020年全年的VTEC日峰值散点图,日峰值散点图更能体现出电离层的周年季节性特性,全年夏季日峰值最小,由于2020年太阳活动属于低活跃,所以全年VTEC整体较小,均在60 TECU以内。VTEC的实测日峰值与GIM内插值相比,全年整体变化趋势基本一致,其差值的均值和标准差分别为3.51 TECU和5.98 TECU,GIM内插值整体上小于实测值,表明在2020年该地区GIM的VTEC日峰值被整体低估。
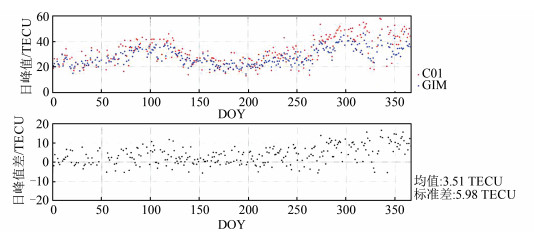 |
| 图 4 2020年C01卫星穿刺点处VTEC日峰值和峰值差 Fig.4 Daily Peak Values and Peak Differences of VTEC at Puncture Point of C01 Satellite in 2020 |
为了进一步分析GIM格网产品在该地区每日的精度水平,本文计算并统计了每天内每历元(30 s)实测值与GIM内插值的差值的日均值和标准差,结果如图 5所示。从均值上看,全年日均值整体在-4~3 TECU之间波动,模型高估和低估不存在明显的季节性特性;从标准差上看,存在明显季节性特性,在夏季,日标准差相对较小,计算得到全年的日均值和日标准差的均值分别为-0.87 TECU和3.24 TECU。
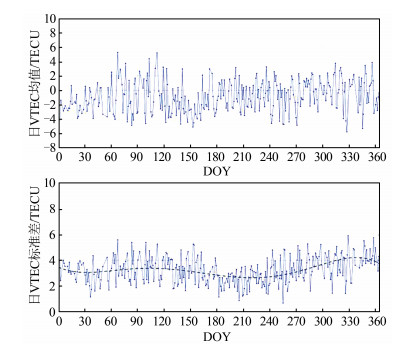 |
| 图 5 2020年C01卫星实测值与GIM内插值差值的日均值和标准差 注:图中黑色断线表示拟合线。 Fig.5 Daily Mean Values and Standard Deviation Values of Measured VTEC and GIM VTEC of C01 Satellite in 2020 |
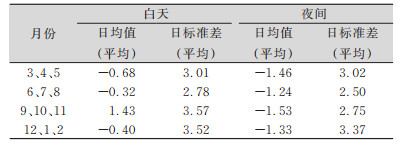
白天由于受太阳辐射,电离层光电效应较强,而夜间几乎消失,本文根据季节的月份进一步统计白天时段(地方时9~18时)和夜间时段(地方时22~次日6时)的GIM内插值与实测VTEC的差异性,各月份的日均值和日标准差的均值统计结果如表 3所示。除9月、10月、11月外,各月份白天时段的日均值均在-1.0 TECU以内,略优于夜间时段均值;从标准差上看,白天时段略大于夜间时段,总月平均分别为3.22 TECU和2.91 TECU;在各月份中,6月、7月、8月白天和夜间的均值和标准差都较小。
| 表 3 2020年各月份白天和夜间时段的统计结果/TECU Tab.3 Statistics for Day and Night Periods in Each Month of 2020/TECU |
 |
3 结束语
本文通过非差非组合PPP反演电离层VTEC,利用北斗GEO卫星的“静地特性”,即固定基站下所北斗GEO卫星穿刺点位置近似不变,相较于其他星座卫星,具有固定穿刺点位置进行电离层的连续实测的优势,对深圳市2020年全年进行连续电离层监测,并将结果与IGS提供的GIM产品进行对比,详细分析了GIM产品与北斗GEO卫星的实测值的差异精度。结果表明:利用北斗GEO卫星进行电离层监测具有实时连续性优势;深圳市2020年的GIM产品与北斗GEO实测值相比,全年变化趋势基本一致,全年差值的日均值和标准差分别为-0.87 TECU和3.24 TECU。日标准差有明显的季节性特性,其中,6月、7月、8月较低,各月份白天时段日均值略优于夜间时段,但全年VTEC日峰值整体偏小,其差值的均值和标准差分别为3.51 TECU和5.98 TECU。
| [1] |
李涌涛, 李建文, 魏绒绒, 等. 全球电离层TEC格网时空变化特性分析[J]. 武汉大学学报·信息科学版, 2020, 45(5): 776-783. |
| [2] |
吴风波, 吴仁攀, 任晓东. 综合多种方法分析中国区域TEC时空变化特征[J]. 大地测量与地球动力学, 2014, 34(5): 75-81. |
| [3] |
卢世坤, 李义红, 李夕海, 等. 太阳平静期地磁场与电离层时空变化相互作用分析[J]. 地球物理学进展, 2019, 34(2): 454-461. |
| [4] |
熊朝晖, 姚宜斌, 袁德宝, 等. 全球单层电离层球谐函数模型计算及精度评估[J]. 测绘地理信息, 2018, 43(4): 20-23. |
| [5] |
吴晓莉, 韩春好, 平劲松. GEO卫星区域电离层监测分析[J]. 测绘学报, 2013, 42(1): 13-18. |
| [6] |
白晓涛, 蔡昌盛. 基于北斗GEO卫星的磁暴期间电离层TEC响应分析[J]. 大地测量与地球动力学, 2020, 40(2): 129-133. |
| [7] |
张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011, 40(4): 447-453. |
| [8] |
赵阳阳, 吕志伟, 贾铮阳, 等. 非差非组合精密单点定位提取区域电离层延迟及精度评定[J]. 测绘与空间地理信息, 2018, 41(5): 122-124. |
| [9] |
Farzaneh S, Forootan E. A Least Squares Solution to Regionalize VTEC Estimates for Positioning Applications[J]. Remote Sensing, 2020, 12(21): 3545. |
| [10] |
申健, 赵文, 安向东. 基于非组合精密单点定位的区域电离层建模[J]. 测绘地理信息, 2019, 44(6): 31-34. |
| [11] |
Wang J, Huang G W, Zhou P Y, et al. Advantages of Uncombined Precise Point Positioning with Fixed Ambiguity Resolution for Slant Total Electron Content (STEC)and Differential Code Bias(DCB)Estimation[J]. Remote Sensing, 2020, 12(2): 304. |
| [12] |
周锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018
|
| [13] |
李子申, 王宁波, 袁运斌. 多模多频卫星导航系统码偏差统一定义与处理方法[J]. 导航定位与授时, 2020, 7(5): 10-20. |
| [14] |
温晋, 万卫星, 丁锋, 等. 电离层垂直TEC映射函数的实验观测与统计特性[J]. 地球物理学报, 2010, 53(1): 22-29. |
| [15] |
李涌涛, 赵昂, 李建文, 等. 单站区域电离层TEC建模及精度分析[J]. 武汉大学学报·信息科学版, 2022, 47(1): 69-78. |
 2022, Vol. 47
2022, Vol. 47


