| 基于全球台站的GNSS卫星精密定轨策略分析 |
2. 武汉大学测绘学院,湖北 武汉,430079;
3. 舟山市国土资源局,浙江 舟山,316000
2. School of Geodesyand Geomatics, Wuhan University, Wuhan 430079, China;
3. Zhoushan Bureau of Land Resource, Zhoushan 316000, China
自20世纪70年代GPS建立开始,精密定轨作为导航卫星系统的关键技术,一直是该领域的研究热点。尤其是1994年国际GNSS服务组织(International Global Navigation Satellite System Service, IGS)成立以来,国内外学者对卫星定轨技术作了大量研究,同时在很多领域不断取得突破。Amold等[1]发现在太阳-卫星连线方向只有偶数阶的光压谐波摄动,而在其他两个垂直方向值存在奇数阶的摄动。文献[2, 3]分别对轨道摄动力模型进行分析,发现适当增加经验力对轨道精度的有一定改善作用。在卫星轨道预报方面,车通宇等[4]利用SDP4模型对卫星轨道预报取得了较好的效果。目前, IGS下属多个数据分析中心定期发布的相应的卫星产品,包括卫星轨道、卫星钟差和对流层延迟等,IGS通过融合多个分析中心的结果,向大众发布的最终卫星轨道精度可达2.5 cm,钟差精度优于0.075 ns[5]。
对于导航卫星而言,轨道确定一般采用动力学定轨,该方法涉及到轨道力学模型和卫星观测方程的建立和处理。根据观测方程建立时观测量组合方式的不同,定轨一般有非差和双差两种方法。非差方式具有测量间独立性较好而且可同步估计钟差等优势,双差则能有效地减少待估参数的个数,总体而言两种方法各有特点。目前,已经有很多学者[6-9]基于非差或双差方式解算卫星精密轨道,党金涛等[10]分析了测站分布对定轨精度的影响,但针对定轨过程中多个因素或解算策略对轨道精度影响进行细致的分析的研究还比较少。
本文基于双差模式设计了一套相应的卫星定轨方案,并采用全球分布的近80个IGS跟踪站数据验证了方案的可行性和精度。本文还详尽地分析了站坐标约束、光压模型、大地测量参数、弧段长度等因素对定轨精度的影响,以IGS最终精密星历作为参考,评估了本文最终获取的GNSS轨道的精度。
1 数据处理方法 1.1 精密定轨基本原理卫星的受摄运动轨道是在二体问题的基础上加上摄动力来推求的,因而力学模型和观测方程的精度是决定定轨精度最关键的因素。由于卫星的状态转移矩阵和轨道初值的求定涉及到卫星变分方程和运动微分方程的求解,因而处理过程复杂。略去推导过程,将双差观测方程线性化可直接获得用于估计轨道参数、光压参数为:
| $ \begin{array}{c}{L C_{k l}^{i j}(t)=\rho_{k l}^{i j}\left(t, X_{r 0}, X^{S}(t)\right)+\frac{\partial \rho_{k l}^{i j}}{\partial X_{r}} \Delta X_{r}+} \\ {\frac{\partial \rho_{k l}^{i j}}{\partial X^{S}(t)} \boldsymbol{\theta}\left(t, t_{0}\right) \Delta X^{S}\left(t_{0}\right)+\Delta T_{k l}^{i j}(t)+\lambda_{c} N_{k l}^{i j}+\varepsilon_{\Phi}^{\prime}}\end{array} $ | (1) |
式中, LCklij为地面站k、l对卫星i、j的双差组合观测值; ρklij为相应的双差站星距; θ(t, t0)为状态转移矩阵; Tklij(t)为对流层延迟; λc为组合相位观测值的波长; Nklij为相位模糊度;Xr0为测站近似坐标; ΔXr为测站坐标改正; XS(t)为卫星相应的轨道参数及力学参数(包括经验力参数、光压参数等); ΔXS(t0)为参考历元t0的轨道参数的改正; ε′Φ为相应的观测噪声。根据最小二乘原理利用方程(1)可估计相应的轨道参数或其他参数。
1.2 定轨基本策略及流程在处理GNSS数据时为获得高精度的定轨结果,各项误差均加于考虑,其中海洋潮汐影响、大气潮汐影响等通过先验模型修正;对流层延迟根据Saastamoinen模型计算,映射函数采用GMF(glo-bal mapping function)模型;地球自转和相对论效应影响等根据IERS2010协议加以修正;多路径效应通过高度角加权来削弱。其他有些误差项则作为未知参数估计,所有涉及的模型及误差处理策略总结如表 1所示,表 1中ECOM(extended CODE orbit model)为光压模型,CODE为欧洲定轨研究中心(center for orbit determination in Europe),EOP为地球自转参数(earth orientation parameters)。
| 表 1 GNSS定轨基本策略及相关误差处理模型 Tab.1 Basic Strategies and Error Models for Precise Orbits Determination of GNSS |
 |
本文基于Bernese GNSS Software软件,采用双差方式设计了一套GNSS卫星精密定轨方案[11-14],整个定轨数据处理流程如图 1所示,该定轨流程主要包含以下4部分:①数据准备、格式转换部分:包括广播星历的合并及格式转换、观测数据格式转换、测站当前坐标推算等;②数据预处理部分:包括接收机钟差同步、基线生成及选择、周跳探测修复、数据筛选等;③轨道初步更新:根据观测数据获得浮点解结果,初步解算卫星轨道参数,并对先验轨道进行更新;④最终轨道确定:利用更新的卫星轨道求取固定解结果,同时准确估计卫星轨道参数,根据轨道参数获取卫星轨道坐标。
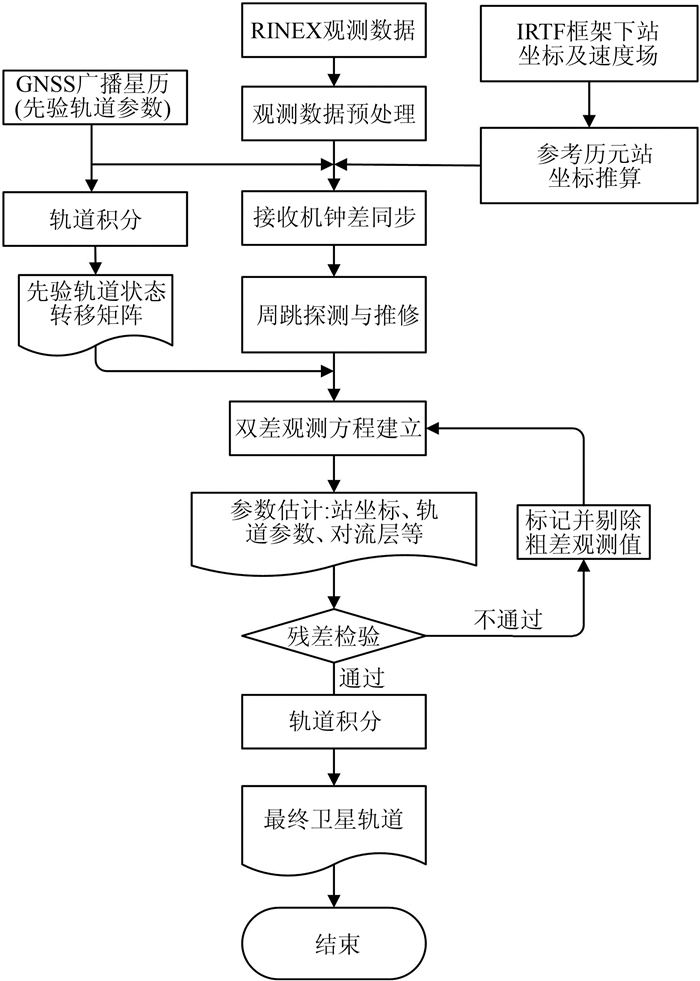 |
| 图 1 GNSS卫星定轨流程 Fig.1 Flow Chart of Precise Orbits Determination of GNSS |
2 精密定轨数据处理及结果分析 2.1 实验数据及解算策略
测站分布和测站数量对定轨结果有一定程度的影响,考虑到数据处理所需时间,本文从全球近500个IGS跟踪站中择优选取了80个左右的观测站,并下载了2015年各测站(年积日:337~365)近一个月的观测数据用于定轨实验计算。这些测站大部分都能同时跟踪GPS和GLONASS卫星且均属于IGB08框架下站点,因而测站比较稳定,所选测站的分布情况如图 2所示。
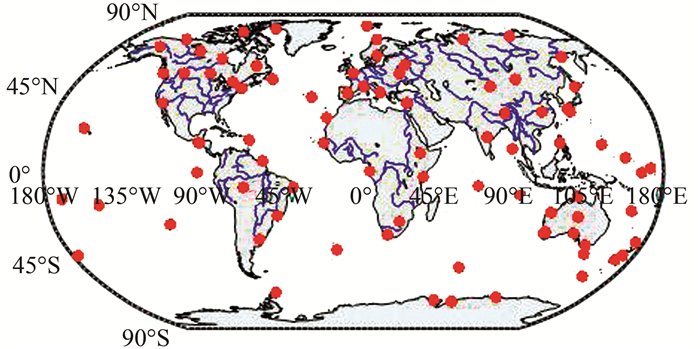 |
| 图 2 IGS站站布图 Fig.2 Distribution of IGS Stations Used in This Study |
2.2 单天定轨结果精度分析
为评价定轨结果的精度(采用表 1中定轨策略,以下称基本策略),此处将IGS最终精密星历作为参考,图 3分别给出了GPS-01和GLONASS-01卫星定轨结果和IGS公布值之间的差异。由图 3可知,卫星一天的轨道在径向(radial)、切向(along-track)和法向(cross-track)的差异基本上保持在15 cm之内,轨道差异较小,具有较高的精度。
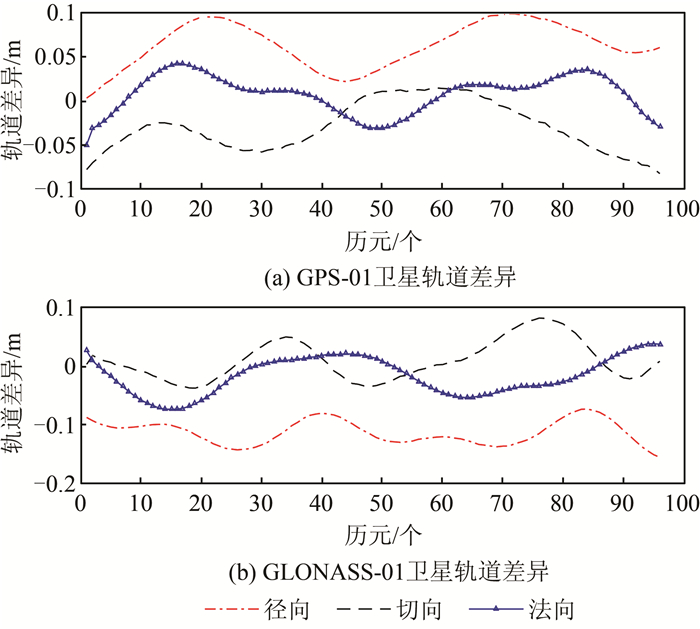 |
| 图 3 卫星轨道与IGS差异 Fig.3 Differences Between Our Orbits and IGS Final Orbits |
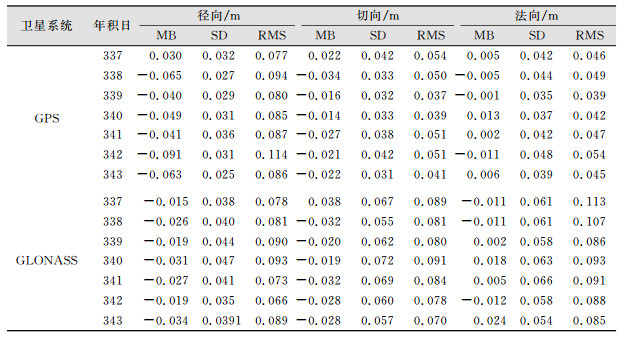
此外,以年积日337~343为例,表 2给出了所有GNSS卫星定轨结果和IGS公布值之间差异的平均偏差(mean bias, MB)、标准差(standard deviation, SD)和均方根(root mean square, RMS)的均值等统计结果。整体而言,GPS卫星的定轨结果优于GLONASS卫星。由表 2还可看出,卫星轨道精度在径向最优,法向和切向精度相当,因为标准差在径向最小,法向和切向标准差相当。但是由于GPS和GLONASS定轨结果在径向和切向均存在几cm的系统性差异(MB不为0),而在法向无明显的系统性差异,导致径向和切向RMS较大。GPS卫星连续7天定轨结果在径向、切向、法向和3D平均RMS分别为0.089 m、0.046 m、0.046 m、0.110 m,GLONASS卫星连续7天定轨结果在径向、切向、法向和3D的平均RMS分别为0.081 m、0.081 m、0.095 m和0.149 m。
| 表 2 定轨结果和IGS轨道差异统计 Tab.2 Statistical Results of the Differences Between Our Orbits and IGS |
 |
2.3 不同策略定轨精度对比分析
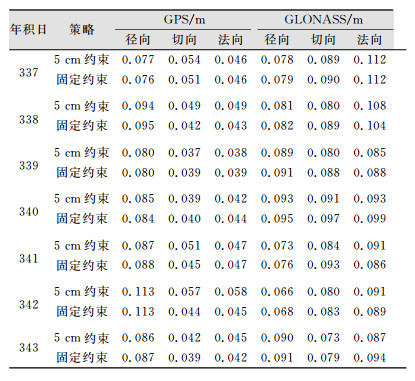
1) 不同站坐标约束影响分析。准确的站坐标对卫星定轨至关重要,为分析不同的站坐标约束对定轨结果的影响,本文对比了站坐标采用5 cm松约束和坐标固定约束策略。表 3给出了2种不同策略下卫星轨道精度对比。和表 2(2 cm强约束)结果对比可知,3种不同站坐标约束策略对定轨结果影响均较小,不同的策略在各个方向引起平均差异最大不超过10 mm,这是由于本文所采用的测站坐标来自IGB08框架,同时还考虑了测站速度引起的测站漂移,因而用于GNSS数据处理具有较高精度。
| 表 3 不同坐标约束下卫星轨道精度对比 Tab.3 Comparison of theAccuracy with Different Coordinate Constrains |
 |
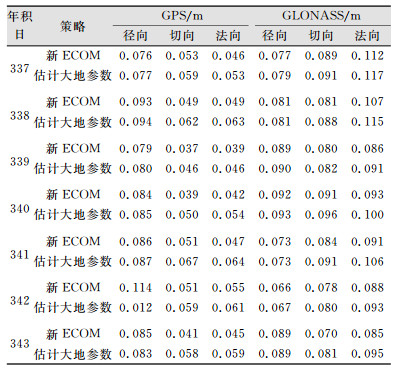
2) 光压模型及同步估计大地参数影响分析。光压模型一直是制约着卫星定轨精度的关键技术之一,CODE早在90年代初就提出了ECOM光压模型,随后一直被广泛采用。近年来随着研究的深入,Arnold等[1]人发现,在卫星-太阳连线方向上只有偶数短周期项光压摄动,而在另外两个垂直方向上仅有奇数项摄动,因此,CODE在2015年提出了一种新的ECOM模型。地心坐标参数直接影响这参考基准框架,同时地球自转参数(earth rotation parameters, ERPs)又影响着卫星天球坐标和地固坐标之间的转换精度,从而直接影响卫星轨道的精度。笔者分别分析了新ECOM光压模型和增加估计大地参数后卫星定轨精度变化,其结果如表 4所示。由表 4可知,新ECOM光压模型对卫星轨道精度有细微的改善。然而,增加估计大地参数后卫星轨道精度明显下降,在单个方向影响可能超过10 mm,这是由于增加估计大地参数后,其估计误差将传播至卫星轨道中,而基本策略中大地参数直接固定为IGS周解。IGS周解中的ERPs等参数由于综合了多天的数据而具有更高的精度,通过和IERS C04公布的ERPs对比,也可证实本文同步估计的ERPs参数精度更差。因此,基本策略中大地参数直接采用IGS周解时取得了更好的定轨精度。
| 表 4 不同光压模型和大地参数策略下卫星轨道精度对比 Tab.4 Comparison of the Accuracy with Different Strategies of Solar Radiation Model and Geodetic Parameters |
 |
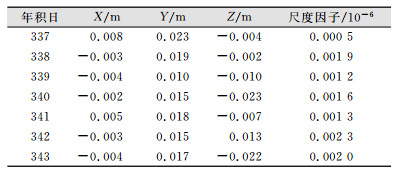
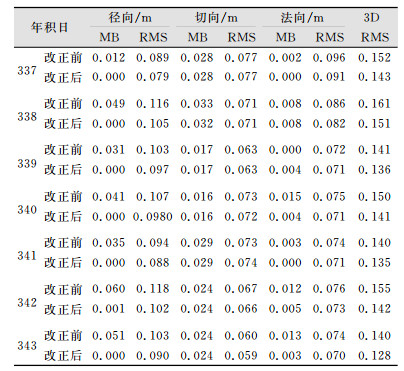
3) 一致性改正分析。理论上卫星轨道的比较应该在统一的基准框架下进行,然而不同的观测数据、测站分布和测站数量等均会造成解算的轨道产品不在完全相同的框架下。IGS发布的最终精密星历也是在消除各个数据分析中心测站网基准差异后综合多个中心的产品获得的,将本文轨道结果和IGS公布值比较之前,应先做框架基准一致性改正。由于动力学方程的约束,使轨道对地心比较敏感,各个测站网基准相对于IGS框架的偏移不会对轨道原点产生显著影响[22],此处一致性改正时,认为基准间无整体旋转,只考虑坐标框架间的整体平移和尺度改正。表 5列出了连续7天定轨基准和IGS轨道基准间的差异。由表 5可知,两框架基准在X和Z方向符合较好,差异仅有几mm;而在Y方向基准差异达到了1~2 cm,也就是说如果不顾忌一致性改正,将可能引入1~2 cm左右的系统性的轨道差异。为进一步说明轨道一致性改正后,卫星轨道精度的变化情况,表 6分别列出了一致性改正前后定轨结果和IGS平均差异的统计结果。由表 6可知,一致性改正后,轨道在径向平均差异(MB)由原来的几cm趋近于0.0 cm,这是因为轨道径向误差跟基准尺度强相关,尺度因子可以吸收该部分误差。此外,由表 6也可看出,一致性改正后,GNSS卫星轨道3D误差平均提高了将近1 cm。但是框架一致性改正后,轨道在径向仍存在一定的系统性偏差,表现为径向精度不如法向和切向精度。
| 表 5 坐标基准和IGS坐标基准差异 Tab.5 Difference of Datum Frame Between Our Result and IGS |
 |
| 表 6 一致性改正前后轨道差异对比 Tab.6 Comparison of the Differences Before and After the Consistency Correction |
 |
4) 3天综合轨道精度分析。由于弧段长度的限制,单天轨道具有使用的观测值有限、相邻轨道边值不连续等缺点,常常通过单天解法方程叠加的方式来获得更为准确的综合轨道。综合以上各策略分析结果,此处进行轨道叠加所用的单天解是基于如下最优策略获得的:①2 cm测站坐标约束;②地球自转参数固定为IGR结果,不估计地心坐标参数;③采用新的ECOM模型;④增加框架一致性改正。此外,弧段叠加时在边界处各添加一组随机参数,获得3天综合轨道,以中间一天轨道结果为当天最终综合结果。除去第一天和最后一天,图 4给出了年积日338~364连续综合轨道各颗卫星的平均精度,对出现轨道机动的卫星,不统计机动当天的轨道精度。由图可知,GPS各卫星轨道差异单方向均在15 cm以内,GLONASS卫星各卫星轨道差异大部分在20 cm以内。所有GPS卫星平均轨道精度在径向、切向、法向和3D分别为:0.075 m、0.046 m、0.044 m、0.098 m; 所有GLONASS卫星平均轨道精度在径向、切向、法向和3D分别为:0.079 m、0.071 m、0.086 m、0.137 m。与§2.2节中所用基本策略获得的单天轨道精度相比,GPS和GLONASS综合解轨道三维精度分别提高了10.9%和8.1%,但仍然可以看出,部分卫星在径向还存在系统性偏差。
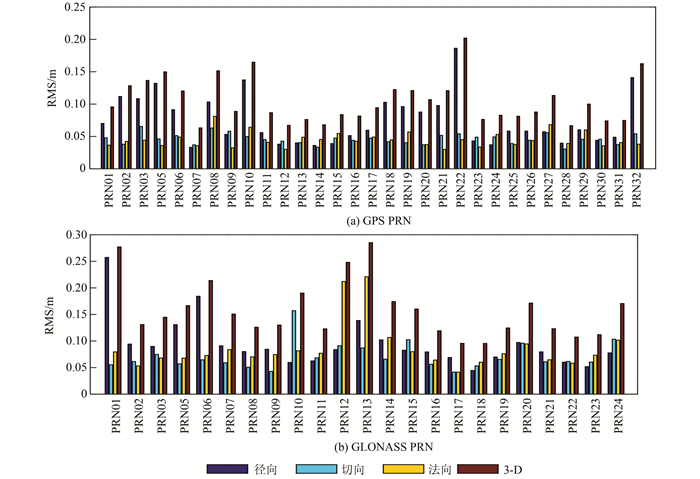 |
| 图 4 GNSS卫星定轨精度统计 Fig.4 Statistical Results of Precise Orbits Determination of GNSS |
3 结束语
本文基于双差数据处理模式设计了一套卫星精密定轨的方案,通过全球IGS站数据验证了方案的可行性。结果表明,本文设计的定轨方案获得的轨道,GPS和GLONASS卫星单天3D精度分别可以达到11cm和15 cm。此外,本文还实验还指出,不同的卫星光压模型和站坐标约束对轨道影响在mm级,而准确的大地参数和框架一致性改正对轨道的改善可达1~2 cm。文中通过综合多个改进的定轨策略,最终获取的GPS卫星轨道三维平均精度优于10 cm,GLONASS卫星轨道三维精度优于14 cm。GPS和GLONASS卫星轨道的整体精度较基本策略提高了10%左右。需要指出的是,本文最终结果和IGS最终精密星历相比仍然存在一定差距,此外本文所获得的轨道在径向还存在几cm的系统差,这可能与测站数量、定轨弧段长度、未考虑地球反照率和随机参数设置等其他定轨策略相关。要获取更精确的卫星轨道还需进一步的研究分析。
| [1] |
Amold D, Meindl M, Beutler G, et al. CODE's New Solar Radiation Pressure Model for GNSS Orbit Determination[J]. Journal of Geodesy, 2015, 89(8). DOI:10.1007/s00190-015-0814-4 |
| [2] |
赵齐乐.GPS导航星座及低轨卫星的精密定轨理论和软件研究[D].武汉: 武汉大学, 2004
|
| [3] |
Jäggi A, Hugentobler U, Beutler G. Pseudo-Stochastic Orbit Modeling Techniques for Low-Earth Orbiters[J]. Journal of Geodesy, 2006, 80(1): 47-60. DOI:10.1007/s00190-006-0029-9 |
| [4] |
车通宇, 杨力, 张传定, 等. SDP4模型用于北斗导航卫星轨道预报的精度分析[J]. 测绘地理信息, 2017, 42(2): 12-16. |
| [5] |
Shi Junbo, Wang Gaojing, Han Xianquan, et al. Impacts of Satellite Orbit and Clock on Real-Time GPS Point and Relative Positioning[J]. Sensors, 2017, 17(6). DOI:10.3390/s17061363 |
| [6] |
施闯, 赵齐乐, 李敏, 等. 北斗卫星导航系统的精密定轨与定位研究[J]. 中国科学:地球科学, 2012, 42(6): 854-861. |
| [7] |
陈俊平, 张益泽, 谢益炳, 等. 超大观测网络及多GNSS系统的快速数据处理[J]. 武汉大学学报·信息科学版, 2014, 39(3): 253-257. |
| [8] |
盛传贞, 袁运斌, 孙保琪, 等. 基于全球IGS数据的GPS导航星座精密轨道确定[J]. 大地测量与地球动力学, 2011, 31(1): 138-141. |
| [9] |
刘伟平, 郝金明, 于合理, 等. 导航卫星精密轨道与钟差确定方法研究及精度分析[J]. 测绘通报, 2014(5): 5-7. |
| [10] |
党金涛, 郭东晓, 李建文, 等. 导航卫星非差精密定轨测站选取策略分析[J]. 大地测量与地球动力学, 2015, 35(6): 997-1000. |
| [11] |
Ray R D, Ponte R M. Barometric Tides from ECMWF Operational Analyses[J]. Annales Geophysicae, 2003, 21(8): 1897-1910. DOI:10.5194/angeo-21-1897-2003 |
| [12] |
Steigenberger P, Hugentobler U, Hauschild A, et al. Orbit and Clock Analysis of Compass GEO and IGSO Satellites[J]. Journal of Geodesy, 2013, 87(6): 515-525. DOI:10.1007/s00190-013-0625-4 |
| [13] |
Steigenberger P, Hugentobler U, Montenbruck O, et al. Precise Orbit Determination of GIOVE-B Based on the CONGO Network[J]. Journal of Geodesy, 2011, 85(6): 357-365. DOI:10.1007/s00190-011-0443-5 |
| [14] |
魏娜, 施闯, 李敏, 等. IGS产品的一致性分析及评价[J]. 武汉大学学报·信息科学版, 2009, 34(11): 1363-1367. |
 2019, Vol. 44
2019, Vol. 44

