| 基于国家坐标系的独立坐标系建立新方法 |
在不动产测量中,顾及与二次土地调查成果的衔接,更多考虑到未来城乡一体化地籍管理的需要和“一张图”工程的需要,确权登记发证:平面坐标系统宜采用1980西安坐标系统,高程系统宜采用“1985国家高程基准”[1]。
为便于数据管理,同时顾及地方经济能力和确保测量的几何精度,根据文献[1]的要求,中央子午线按照地图投影标准3°带的标准方法选定。对于各投影带长度变形值不大于2.5 cm/km的区域,投影方法自动设置为高斯-克吕格投影。当长度变形值大于2.5 cm/km时,所测坐标的投影面为各城镇村庄坐标起算点高程值的高程面(测区或建筑物平均高程面),但不进行高程抵偿计算。这种平面坐标系统可称为基于1980西安坐标系椭球参数的独立平面直角坐标系统,可简称为独立坐标系统或挂靠坐标系[1, 2]。为便于叙述,以下均称为挂靠坐标系。
挂靠坐标系的最大优点就是其坐标成果与国家统一的3°带坐标成果比较接近,无需换带计算和不同坐标系之间的换算,便于设计和施工部门使用。但其边长不进行高斯投影改正,仅适用于测区范围不大或者测区位于中央子午线两侧且高程变化不大的工程[2]。而对于测区范围较大且离中央子午线较远的工程,比如某县不动产测绘工程,如何建立满足条件的挂靠坐标系,以解决长度投影变形过大的问题。为此,本文通过对引起投影长度变形原因的分析,探讨了实现挂靠坐标系的新思路,结合实例并给予验证。
1 投影长度变形分析地籍控制网的布设遵循“从整体到局部、分级布设”的原则,分首级控制网和图根控制网[3]。首级控制网点的等级分为三、四等或D、E级和一、二级。三、四等或D、E级控制点主要采用静态全球定位系统定位方法建立,一、二级控制点和图根控制点可采用导线测量方法施测,也可采用基于单基站或网络或CORS(continuously operating reference system)的RTK方法施测。在首级控制点的基础上,以地籍子区为单元,布设图根控制点,获得图根控制点的挂靠坐标系坐标,以这些点作为起算点进行碎部测量,投影长度变形可控制在限差之内。
在测量工作中,实测边长归算至参考椭球面的变形为
| $ \frac{{\Delta {S_H}}}{{{S_H}}} = \frac{{y_m^2}}{{2R_m^2}}\left( {1 - \frac{{{H_m}}}{R}} \right) - \frac{{{H_m}}}{R} $ | (1) |
其中,SH为实测地面边长;Hm为测距边两端点平均大地高程;R为测距边所在方向的椭球曲率半径;S=SH+ΔS1;ym为测距边两端点横坐标的平均值;Rm为测距边中点处在参考椭球面上的平均曲率半径。
由上述可知,投影长度综合变形为ΔS=ΔS1+ΔS2。当综合变形超过允许的精度要求时(0~2.5 cm/km),可令ΔS=0,则有:
| $ {S_H}\left( {\frac{{y_m^2}}{{2R_m^2}}\left( {1 - \frac{{{H_m}}}{R}} \right) - \frac{{{H_m}}}{R}} \right) = 0 $ | (2) |
式中,R与Rm皆取6 371 km。
若采用国家3°带高斯投影平面直角坐标系,不改变中央子午线位置,则通过式(2)计算一个合适的归算高程参考面,可通过改变投影高程面来实现投影长度变形的改正。
2 独立坐标系坐标的实现建立挂靠坐标系成果的图根控制点,常用常规导线测量方法和导线测量+GNSS RTK的方法。单一的导线测量方法比较简单,不再赘述。这里简单介绍导线测量+RTK方法的实现步骤,重点探讨应用GNSS RTK技术建立挂靠坐标系图根控制点的新方法。
1) 导线测量+RTK。挂靠坐标系只是一种高斯平面直角坐标系,可通过导线测量方法建立以测区中心点国家坐标系坐标为起算点的3~4个首级控制点,其平面坐标为挂靠坐标系坐标,然后用GNSS获得这些控制点的WGS-84(World Geodetic System)坐标,求取两套坐标间的转换参数,最后布设图根点。具体步骤如下:
① 划分作业区域,以区域面积较小的地籍子区为单元;
② 在地籍子区的中心部位按照国家坐标系进行起算点的布设和观测;
③ 确定定向点;
④ 采用支导线或闭合导线进行4个首级控制点的观测;
⑤ 利用首级控制点制作转换数学模型;
⑥ 采用RTK在3~5 km的范围内直接布设图根点,完成划定作业区域的控制点布设。
2) GNSS RTK法。目前,一般均采用GNSS静态观测方法布设首级控制网,而且联测国家控制点,通过平差即可获得首级控制点的国家坐标系成果。挂靠坐标系是一种不同于国家坐标系的参心坐标系,其参考椭球中心、长半轴及赤道面与国家坐标系参考椭球相重合,因此通过椭球变换可实现坐标间的互换[5, 6]。国家坐标系成果完全可以通过严密坐标转换模型的计算获得挂靠坐标系成果,然后计算挂靠坐标系与WGS-84坐标系坐标间的转换参数,利用GNSS RTK直接布设图根控制点。依此思路建立挂靠坐标系,文献[7]详细阐述了建立任意带的高斯平面直角坐标系过程,该挂靠坐标系基于国家椭球参数,以椭球面为投影面。建立基于国家坐标系椭球参数,以测区中心坐标起算点高程面为投影面的挂靠坐标系,可按如下步骤实现。
① 在地籍区布设首级控制点,获得控制点的国家坐标系坐标;
② 估算地籍子区的投影长度变形值,由式(2)可知,当ym一定时,可得
③ 取地籍子区中心位置国家坐标系高斯平面坐标(即ym点处,此点处投影长度变形值为0);
④ 利用椭球膨胀法建立该地籍子区挂靠坐标系,即将首级控制点及地籍子区中心点坐标转换为挂靠坐标系坐标[5, 8];
⑤ 依据首级控制点WGS-84坐标或采集其坐标,计算两套坐标间的转换参数;
⑥ 应用RTK布设图根控制点甚至进行碎部测量。已知控制点的挂靠坐标系平面坐标,采用“GNSS点校正”功能,直接校正WGS-84坐标为挂靠坐标系平面坐标[9]。
3 应用实例浠水县农村不动产测量工程,测区范围东经115°~115°38',北纬30°12'~30°49',面积1 949 km2,分15个地籍区,690余个地籍子区,全县统一布设并观测了GNSS D级首级控制网,各地籍区均有了满足要求的D级控制点。某地籍区3°带中央子午线经度为114°,平均高程为100 m,测区距中央子午线距离101.998~119.28 km,经计算,投影长度变形值为11.25~15.96 cm/km,均超过了2.5 cm/km,所以每个地籍子区须建立一个挂靠坐标系,布设挂靠坐标系图根点,然后再进行碎部测量。下面以某地籍子区为例,应用椭球膨胀法建立挂靠坐标系并布设图根点,检验坐标反算边长与测区平均高程面边长,验证其可行性。
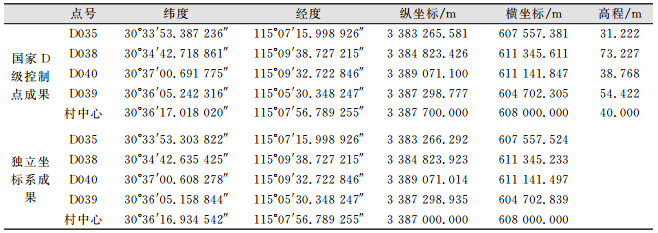
某地籍区GNSS D级控制点测量成果1980西安坐标列于表 1,其中某地籍子区平均纬度为30°35',平均高程为49.41 m,这里忽略高程异常的影响,将平均高程近似为平均大地高,投影中央子午线经度114°,地籍子区中心点纵坐标为3 387 700,横坐标为608 600。由式(2)得高程归化面下移的高度为Hm=925 m,则高程抵偿面的高程为49.41-925=-875.59 m。即把地面实测边长归算到高程抵偿面上,此时地籍子区中心位置的边长两项改正得到完全补偿。平面坐标计算结果列于表 1(坐标偏移Δx=-465.063, Δy=-14.909)。坐标反算其边长与测区平均高程面边长对比结果列于表 2。
| 表 1 国家D级控制点和独立坐标系成果 Tab.1 Results of the National Control Point and Independent Coordinate System |
 |
| 表 2 独立坐标系反算边长与测区平均高程面边长对比表 Tab.2 Results of Grid Distance of Calculating the Inverse Side-length and Average Elevation Surface Side-length |
 |
2000国家大地坐标系已经启用,建立基于CGCS2000椭球参数的独立坐标系,其方法一样。
4 结束语建立以地籍子区为单元的挂靠坐标系,其挂靠坐标系坐标起算点均采用了国家坐标系3°带成果,测区中心点挂靠坐标系坐标与国家统一坐标系坐标一致,其余坐标点坐标也十分接近,有利于挂靠坐标系与测区外之间的联系,便于大面积测区测绘成果的统一[2, 10]。
将首级控制点国家坐标系成果换算成挂靠坐标系成果,用GNSS RTK法建立基于国家坐标系的挂靠坐标系,不仅省去了在每个地籍子区布设起算点及常规导线测量的工作,大大提高了工作效率,而且有效解决了投影长度变形超限的问题。
| [1] |
湖北省加快推进农村集体土地确权登记发证工作领导小组.湖北省宅基地使用权和集体建设用地使用权确权登记发证工作业务培训讲义[R].湖北省加快推进农村集体土地确权登记发证工作领导小组办公室, 武汉, 2013
|
| [2] |
武江伟, 高红光, 朴盛莲, 等. 长距离供水工程测量平面坐标系的选择[J]. 测绘地理信息, 2015, 40(3): 74-76. |
| [3] |
张恒, 王卓, 司岩, 等. 浅述城镇地籍测量中控制测量工作的实施[J]. 全球定位系统, 2010, 35(3): 42-44. DOI:10.3969/j.issn.1008-9268.2010.03.010 |
| [4] |
赵京黔, 张亮, 魏苹, 等. 独立坐标系的建立方法探讨[J]. 科技创新导报, 2009(25): 236-237. |
| [5] |
张宏伟, 康世英. 基于TGO的独立坐标系与国家坐标系转换方法[J]. 地矿测绘, 2010, 26(2): 12-15. DOI:10.3969/j.issn.1007-9394.2010.02.005 |
| [6] |
费联君, 郭忠明, 马波. 国家-工程坐标系理论在云南高原地区的应用[J]. 测绘地理信息, 2016, 41(4): 48-51. |
| [7] |
刘博涛, 袁凌云, 李杰. 基于CGCS2000的独立坐标系建立与应用[J]. 城市勘测, 2016(3): 118-120. DOI:10.3969/j.issn.1672-8262.2016.03.031 |
| [8] |
冯林刚. GPS测量控制网纳入独立坐标系的方法[J]. 地矿测绘, 2000, 16(3): 6-8. DOI:10.3969/j.issn.1007-9394.2000.03.002 |
| [9] |
董家祥, 王笑北, 崔红悦. 在农村地籍测量中平面坐标系的选择问题[J]. 中国科技期刊数据库(工业B), 2015(34): 307-308. |
| [10] |
王亚非. 陆丰核电厂初级网独立坐标系的建立[J]. 北京测绘, 2016(6): 92-95. |
 2018, Vol. 43
2018, Vol. 43

