| 基于惯性系原理的动基座粗对准及其性能影响因素分析 |
2. 苏州挚途科技有限公司,江苏 苏州,215000
2. Suzhou Zhito Technology Co., Ltd., Suzhou 215000, China
全球导航卫星系统/捷联惯导系统(global navi‐gation satellite system/strapdown inertial navigation system, GNSS/SINS)组合导航分为两个阶段:初始阶段和导航阶段。初始阶段主要为惯导提供初始位置、速度和姿态,为进入导航阶段做准备,初始信息的准确获取直接影响到导航阶段的工作性能。其中,位置、速度可由GNSS提供,在此基础上,再由惯导信息确定初始姿态,该过程被称为惯导初始对准。惯导初始对准可分为静基座粗对准和动基座粗对准[1, 2]。在实际对准应用中,由于车辆发动机震动,船舰海上微幅晃动,飞机空中对准,在航空作业中的定位定向系统(position and orientation sys‐tem, POS)由于故障需要重新初始化等,粗对准往往需要在动基座下进行。在动基座下,惯导不能区分重力加速度和视线加速度,因而需要利用外部辅助信息滤去视线加速度。已有的动基座算法均利用外部速度来进行辅助解算,主要分为3类:①iX‐sea公司的Octans光纤陀螺手册中的惯性系对准原理;②建立大航向误差模型的粗对准法[3, 4]; ③利用GPS测速给出航向角,然后采用搜索法求解俯仰角和横滚角[5]。
本文从惯性系对准原理出发,着重讨论了基于比力和速度矢量的两种动基座粗对准的解算方案,通过模拟数据比较了两种解算方案的性能,同时分析了位置和速度误差的影响,然后,采用一组导航级别的惯导实测数据,以检验惯性系对准方法的实用效果,并重点分析了杆臂误差和轨迹机动性对动基座对准的影响。
1 惯性系对准原理和方法当载体运动时,载体坐标系和导航坐标系之间的旋转矩阵是时变的,确定运动状态下的初始旋转矩阵
当地水平坐标系n下的比力方程为:
| $ {\mathit{\boldsymbol{\dot V}}^n} = \mathit{\boldsymbol{R}}_b^n{\mathit{\boldsymbol{f}}^b} - (2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en}^n) \times {\mathit{\boldsymbol{V}}^n} + {{g}^n} $ | (1) |
式中,
式(1)中的变量都是时变的,
| $ \mathit{\boldsymbol{R}}_b^n\left( t \right) = \mathit{\boldsymbol{R}}_{n\left( 0 \right)}^{n\left( t \right)}\mathit{\boldsymbol{R}}_{b\left( 0 \right)}^{n\left( 0 \right)}\mathit{\boldsymbol{R}}_{b\left( t \right)}^{b\left( 0 \right)}\mathit{\boldsymbol{ = R}}_{n\left( 0 \right)}^{n\left( t \right)}\mathit{\boldsymbol{R}}_b^n\left( 0 \right)\mathit{\boldsymbol{R}}_{b\left( t \right)}^{b\left( 0 \right)} $ | (2) |
式中,n(0)、b(0)分别为初始时刻b系与n系凝结形成的惯性系;n(t)、b(t)分别为任意时刻t两坐标系凝结形成的惯性系;
| $ \mathit{\boldsymbol{R}}_{b\left( t \right)}^{\dot b\left( 0 \right)}\mathit{\boldsymbol{ = R}}_{b\left( t \right)}^{b\left( 0 \right)}\mathit{\boldsymbol{\omega }}_{ib}^b \times $ | (3) |
| $ \mathit{\boldsymbol{R}}_{n\left( t \right)}^{\dot n\left( 0 \right)}\mathit{\boldsymbol{ = R}}_{n\left( t \right)}^{n\left( 0 \right)}\mathit{\boldsymbol{\omega }}_{in}^n \times $ | (4) |
式中,×表示叉乘符号,具体运算为将矢量转换为反对称方阵。将
| $ \mathit{\boldsymbol{R}}_b^n\left( 0 \right)\mathit{\boldsymbol{R}}_{b\left( t \right)}^{b\left( 0 \right)}{\mathit{\boldsymbol{f}}^b} = \mathit{\boldsymbol{R}}_{n\left( t \right)}^{n\left( 0 \right)}\left( {{{\mathit{\boldsymbol{\dot V}}}^n} + \left( {2\mathit{\boldsymbol{\omega }}_{ie}^n + \mathit{\boldsymbol{\omega }}_{en}^n} \right) \times {\mathit{\boldsymbol{V}}^n} - {\mathit{\boldsymbol{g}}^n}} \right) $ | (5) |
令
| $ \mathit{\boldsymbol{R}}_b^n\left( 0 \right)\alpha = \beta $ | (6) |
式中,α为任意时刻b系下速度增量转换至b(0)中的积分;β为n系下速度增量的积分。
每过1 s均会得到一组向量满足式(6),随着时间增加,限制条件越来越强,求得的
在此基础上,对式(5)左右两端进行积分,整理可得:
| $ \begin{array}{c} \mathit{\boldsymbol{R}}_b^n\left( 0 \right)\int_0^t {\mathit{\boldsymbol{R}}_{b\left( t \right)}^{b\left( 0 \right)}{\mathit{\boldsymbol{f}}^b}} {\rm{d}}t = \mathit{\boldsymbol{R}}_{n\left( t \right)}^{n\left( 0 \right)}{\mathit{\boldsymbol{V}}^n} - {\mathit{\boldsymbol{V}}^n}\left( 0 \right) + \\ \int_0^t {\mathit{\boldsymbol{R}}_{n\left( t \right)}^{n\left( 0 \right)}\mathit{\boldsymbol{\omega }}_{in}^n \times } {\mathit{\boldsymbol{V}}^n}{\rm{d}}t - \int_0^t {\mathit{\boldsymbol{R}}_{n\left( 0 \right)}^{n\left( t \right)}{\mathit{\boldsymbol{g}}^n}} {\rm{d}}t \end{array} $ | (7) |
令
| $ \mathit{\boldsymbol{R}}_b^n\left( 0 \right)\alpha = \beta $ | (8) |
对于每一个时刻,由捷联惯导系统(strapdown inertial navigation system, SINS)观测值可计算出α,由GPS辅助信息可计算出β。随着观测量的增加,要求每一个时刻的绝对速度矢量均满足式(8),随着时间的增加,限制条件越来越强,求得的
为了便于研究,本文的导航系选为e系,仿真了导航级别惯导的动态数据,惯导器件参数如下:陀螺零偏ε=0.01°/h,陀螺噪声σε=0.1°/
两种方案的速度积分解算需要满足以下条件:①保证每秒b、n系下的速度变化量满足式(6);②从t时刻到起始时刻的b、n系下的速度变化量满足式(8)。
图 1为两种方案的对准结果。由图 1可知,对准开始60 s后,两种方案均获得了较为准确的姿态信息,这表明两种方法在原理上是一致的。俯仰角与横滚角在开始的几个历元内便可满足对准需求,收敛迅速;航向角的收敛时间较长。两种方案均能较快地确定初始姿态,但是航向角收敛过程中的抖动现象差异较大。
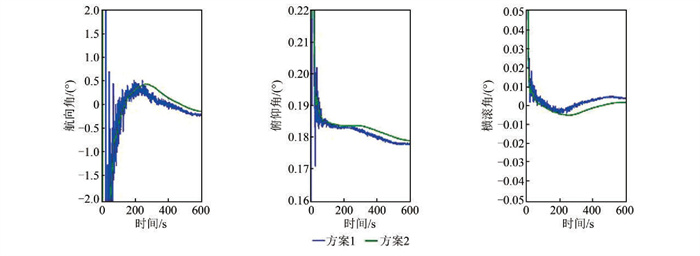 |
| 图 1 两种方案对准结果 Fig.1 Alignment Results of Two Schemes |
2.2 位置误差影响
在两种方案的解算过程中,位置误差对准结果的影响不会太剧烈。本文设置了5组噪声(0.1 m、1 m、10 m、30 m、100 m),其余参数均不变,进行了两种方案的粗对准解算,结果见图 2。
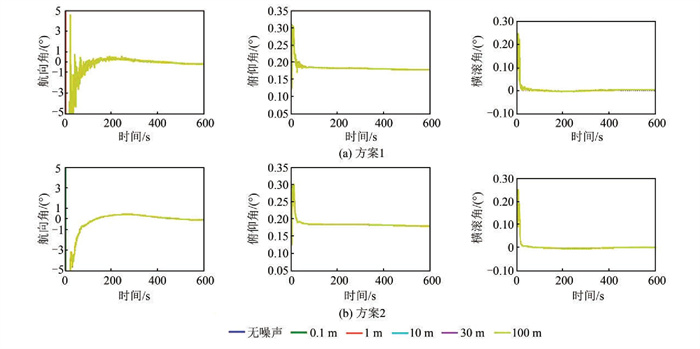 |
| 图 2 位置误差分析 Fig.2 Analysis of Position Error |
5组不同噪声的粗对准结果基本一致,这说明100 m以下的位置误差对两种方案均无影响。
2.3 速度误差影响在GPS测速方面,van Graas等[9]提出了单站测速模型,单站测速精度与多普勒测速精度相当,在0.1 m/s左右。速度直接影响式(6)与式(8)中β相关项的计算,对对准结果有着较大影响[10]。速度误差将直接影响到两种粗对准解算,本文设置了5组噪声(0.01 m/s、0.05 m/s、0.1 m/s、0.5 m/s、1 m/s),其他参数均不变,进行粗对准解算,结果见图 3。
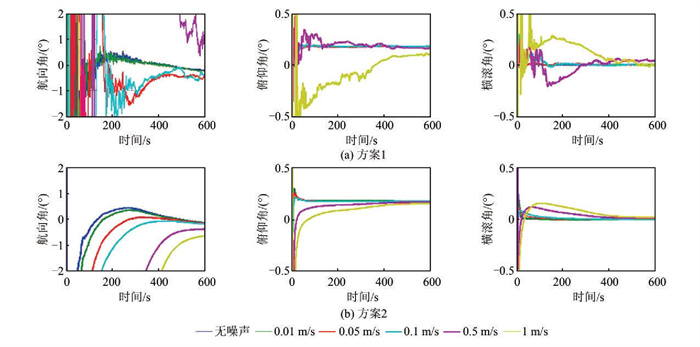 |
| 图 3 速度误差分析 Fig.3 Analysis of Velocity Error |
从图 3可以看出,不同的速度噪声对对准结果的影响非常明显,其中,航向角尤为明显。因为加速度计可以辅助确定俯仰角与横滚角,速度误差小于1 m/s时,两种方案均可以快速地确定航向角、俯仰角及横滚角。但是在速度误差达到1 m/s时,方案1抖动较为剧烈,在600 s内尚未收敛到阈值以内。方案2的收敛过抖动很小,即便速度误差较大,在收敛至1°内后也能够很好地保持角度稳定,约在500 s左右完成了航向角的确定,且结果可靠稳定。航向角较俯仰角与横滚角更难确定。在速度误差小于0.1 m/s时,两种方案在300 s内均可以完成航向角的确定。在速度误差为0.01 m/s、0.05 m/s、0.1 m/s时,方案1分别在约100 s、150 s、200 s完成航向角的收敛,且之后一直保持稳定,较方案2更为有效。当速度误差为0.5 m/s时,方案1在600 s内刚刚达到收敛的阈值角度,但因抖动过大,此时的航向角仍不能使用;方案2约在400 s时航向角收敛至1°以内。
3 实测数据分析本文采用LINS812导航级组合导航设备,在武汉市郊区开阔地带进行跑车实验,观测条件良好。设备部分参数如下:陀螺零偏为0.005°/h,陀螺噪声为0.002 2°/
GPS采用双差解,模糊度全部固定,定位精度为1.0 cm+1.0-3cm,同时用IE浏览器进行了松组合解算,所有结果均通过了IE内部的质量检验。
3.1 实测数据对准结果分析由图 4可知,两种方案均可以完成粗对准姿态确定。同模拟数据对准结果类似,方案1的抖动较为剧烈,在航向角的收敛过程中,会出现到1°以内时因抖动太大并未收敛的情况,最终航向角收敛时间约为160 s;方案2航向角在80 s左右收敛至1°,并且随着时间增加,结果更加准确可靠。俯仰角与横滚角因加速度计性能较好,两种方案在几秒内均可以得到准确可靠的结果。
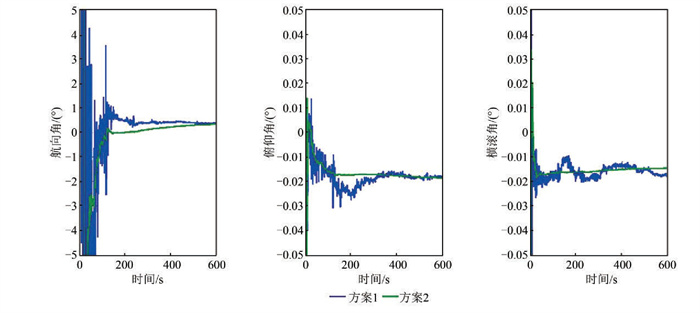 |
| 图 4 实测数据对准结果 Fig.4 Alignment Results of Measured Data |
3.2 不同轨迹对准结果分析
本文从跑车轨迹中选取了4段子轨迹,分别是静态子段1,热车1 min行车子段2,近似直线子段3、高机动性子段4。本文采用两种方案进行粗对准计算,其中因模拟数据与实测数据中加速度计数据质量较高,采用两种方案均可以快速有效地确定俯仰角与横滚角,本文后续的对准结果以航向角的收敛状态进行分析。
由图 5可知,对于4种轨迹,两种方案均能够较为快速准确地解算航向角,方案2较方案1整体上更为稳定可靠;对于不同的轨迹,方案1的抖动剧烈程度不同,方案2较为平稳,对准200 s后,两种方案均可以得到较为稳定准确的对准结果;对于不同机动性的4段轨迹,两种方案均表现出机动性越强,收敛越为快速且抖动越小的特点。
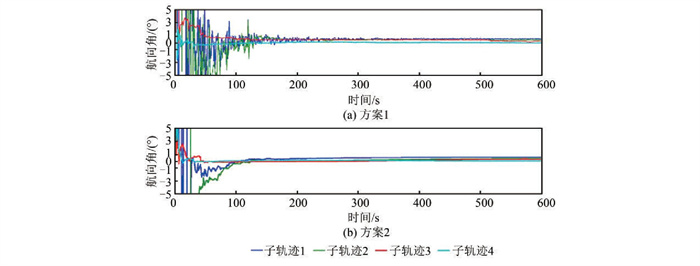 |
| 图 5 不同轨迹航向角对准结果 Fig.5 Yaw Angle Results of Different Trajectories |
3.3 实测数据杆臂改正影响
本文针对较强机动性子段4进行了杆臂修改与否的对准结果对比。对于实测得到的杆臂值,进行8组(±0.05 m、±0.1 m、±0.5 m、±1 m)扰动,分析了不同精度的杆臂测量值对对准结果的影响。
1) 高机动情况下的杆臂影响。本文对子轨迹4利用两种方案进行了粗对准实验,对航向角的收敛结果进行了分析,结果见图 6。采用两种方案进行杆臂改正后,得到的对准曲线与直接使用IMU中心速度进行粗对准的对准曲线基本吻合,这验证了杆臂改正算法的正确性与有效性。方案1的对准时间从约200 s加快到10 s,且收敛过程中的抖动趋于缓和;杆臂改正前,方案2的收敛时间约为40 s,而方案1的约为200 s。随着时间的增加,方案2杆臂的影响基本消除,说明方案2受杆臂误差的影响不太敏感。
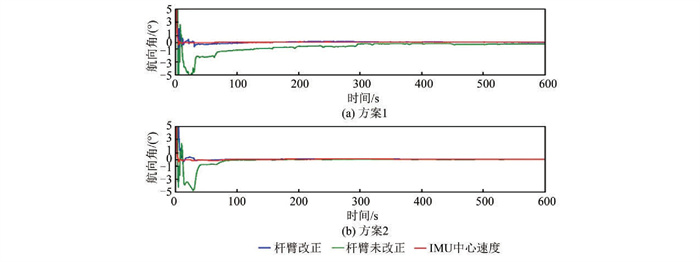 |
| 图 6 高机动性杆臂误差影响 Fig.6 Error Effect of High Maneuverability Lever Arm |
2) 杆臂测量精度的影响。本文对跑车实验测得的杆臂值进行8组(±0.05 m、±0.1 m、±0.5m、±1 m)扰动,分析了不同精度的杆臂测量值对对准结果的影响。
由图 7可知,高机动状态下,杆臂测量值误差达到±0.5 m时,两种方案的收敛时间均从10 s加长到了20 s;杆臂测量值误差达到±1 m时,两种方案的收敛时间均增加到了30 s。杆臂测量值偏差使对准时间明显加长;杆臂测量值偏大或偏小对收敛的中间状态值造成明显的系统偏差。方案1在航向角收敛后,因杆臂测量存在误差,在后续转弯中出现了较为明显的系统偏差,且测量值精度越低,系统偏差越大;方案2在航向角收敛后,速度积分过程会让杆臂测量偏差造成的影响逐步降低,不同测量精度的杆臂值收敛结果基本一致;杆臂测量精度达到0.1 m时,基本不会对两类粗对准结果造成影响。
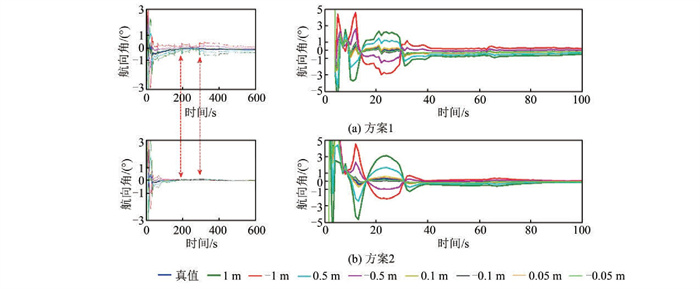 |
| 图 7 杆臂测量精度 Fig.7 Measured Precision of Lever Arm |
4 结束语
本文分析了两种基于优化的动基座粗对准与速度积分动态的粗对准算法,通过对模拟数据与实测跑车数据对准结果的分析,得出以下结论:
1) 在动基座粗对准过程中,位置误差对结果的影响很小,GPS单点定位的精度即可以满足解算需要。
2) 测速的精度在动态粗对准中具有决定性影响,针对目前GPS的测速水平,对准时间建议不少于5 min。
3) 不同轨迹的航向角收敛时间不同,机动性越强,可观测性越高,航向角的收敛速度越快,为了适应各种轨迹下的对准,速度积分的动基座粗对准方案较为稳健。
4) 轨迹平滑时,杆臂效应的影响较小,但在高机动运动情况下,杆臂的影响不可忽略,且杆臂的测量误差不应超过0.1 m。在杆臂不明确或测量精度较低的情况下,可采用速度积分动态粗对准的方法。
| [1] |
惯性导航初始对准[M]. 南京: 东南大学出版社, 1998.
|
| [2] |
静基座捷联惯导解析法对准研究[J]. 武汉大学学报·信息科学版, 2018, 43(2): 201-206. |
| [3] |
捷联惯导系统大失准角下的初始对准研究[J]. 航空计算技术, 2012, 42(4): 39-42. DOI:10.3969/j.issn.1671-654X.2012.04.010 |
| [4] |
简化UKF滤波在SINS大失准角初始对准中的应用[J]. 中国惯性技术学报, 2008, 16(3): 253-264. |
| [5] |
钱伟行. 捷联惯导与组合导航系统高精度初始对准技术研究[D]. 南京: 南京航空航天大学, 2010.
|
| [6] |
Wu M P, Wu Y X, Hu X P, et al. Optimization-Based Alignment for Inertial Navigation Systems: Theory and Algorithm[J]. Aerospace Science and Technology, 2011, 15(1): 1-17. DOI:10.1016/j.ast.2010.05.004 |
| [7] |
Wu Y X, Pan X F. Velocity/Position Integration Formula Part I: Application to In-Flight Coarse Alignment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(2): 1 006-1 023. DOI:10.1109/TAES.2013.6494395 |
| [8] |
Ban Y L, Zhang Q, Niu X J, et al. How the Integral Operations in INS Algorithms Overshadow the Contributions of IMU Signal Denoising Using Low-Pass Filters[J]. Journal of Navigation, 2013, 66(6): 837-858. DOI:10.1017/S0373463313000465 |
| [9] |
van Graas F, Soloviev A. Precise Velocity Estimation Using a Stand-Alone GPS Receiver[J]. Navigation, 2004, 51(4): 283-292. |
| [10] |
捷联惯性系粗对准误差及数值问题分析[J]. 中国惯性技术学报, 2010, 18(6): 648-652. |
 2021, Vol. 46
2021, Vol. 46


