| 基于电离层线状变化特征的电离层建模方法 |
2. 武汉大学中国南极测绘研究中心,湖北武汉,430079
2. Chinese Antarctic Center of Surveying and Mapping, Wuhan University, Wuhan 430079, China
全球导航卫星系统(global navigation satellite system,GNSS)信号传播过程中在电离层内部的折射和偏移是造成GNSS定位过程中电离层延迟的主要原因[1-3]。一般使用电离层总电子含量(total electron content,TEC)来描述电离层状态。电离层内部存在固定的变化规律,影响电离层变化的主要因素有当地太阳辐射量和地磁变化[4, 5]。根据这些规律和影响电离层的因素,电离层建模方法主要有两种:①利用其变化规律,基于大量数据建立的电离层经验模型,这种模型包括Bent模型、随卫星广播星历播发的Klobuchar模型、国际参考电离层(international reference ionosphere,IRI)模型和NeQuick2模型等,其中,Klobuchar模型作为简单的经验模型,仅能对电离层误差进行50% 的修正[6];最新的IRI模型为IRI-2016,它在原来模型的基础上添加了磁暴模式,可选择不同的物理观测量来定制化求解电离层相关信息,如与太阳活动有关的F10.7、太阳黑子数等[7];NeQuick2模型可以根据太阳活动指数和地理位置、地方时等信息,直接求解接收机和卫星间的斜路径总电子含量(slant TEC,STEC),其精度为2~7 TECU[8]。②基于实测观测值建立的数学模型,如国际GNSS服务(International GNSS Service,IGS)组织发布的全球电离层模型(global ionospheric model,GIM)和区域性的电离层模型,是目前最可靠的TEC全球模型之一,但其精度区域差异性较大,在欧洲等数据分布较密区域的精度可达2 TECU[7, 9]。常用的电离层TEC内插方法有反距离加权法、克里金插值法[10]、模型插值法等,其中,模型插值法的可选模型有多项式模型、三角函数模型、球谐模型、球冠模型等[11]。
在建模过程中,考虑到电离层内部的电子并不是完全自由运动的,会受到电磁场的作用及太阳辐射影响,电离层在线状区域(地理经线或地磁经线)内的变化更有规律,使用面状区域内的测站进行建模插值可能会因为引入了全方向测站数据而降低了数据的规律性,导致建模精度降低[12]。本文利用电离层在线状区域内的分布特点建立数学模型,将STEC作为原始观测值进行内插建模,获得待求点的电离层信息,并将其与基于面状区域的建模结果进行比较。
1 原理与方法电离层受到太阳辐射、地磁、大气氧氮浓度、大气潮汐等内部因素的影响[13],其变化特征从数理角度来看,可以将其视为位置与时间等变量的函数:
| $ T_e=F(\boldsymbol{P}, T) $ | (1) |
式中,Te表示TEC;P为位置向量;T为时间变量。
本文主要研究在同一时刻,同一地理经度链、地理纬度链或地磁经度链内不同地点的电离层状态,因此,上述函数可以简化为如下形式:
| $ T_e=F\left(\boldsymbol{P}_l, T_0\right)=F\left(\boldsymbol{P}_l\right) $ | (2) |
式中,Pl为所选的线状分布的测站位置;T0为所选时刻。根据泰勒展开公式,可以将其展开为如下形态:
| $ \begin{gathered} F\left(P_0\right)=\sum\limits_{n=0}^{\infty} \frac{F^{(n)}\left(P_i\right)}{n !}\left(P_0-P_i\right)^n=F\left(P_i\right)+ \\ \frac{F\left(P_i\right)}{1}\left(P_0-P_i\right)+\frac{F^{(2)}\left(P_i\right)}{2 !}\left(P_0-P_i\right)^2+\cdots \end{gathered} $ | (3) |
式中,P0为待插值点的纬度或经度,视建模区域方向而定;Pi为STEC观测值纬度。由于真值固定,且理想情况下认为观测值为观测点处的STEC真值,因此,误差主要产生在等式右侧微分项部分。当站点间距固定时,电离层变化梯度越小,模型插值结果与真值越相近。上面讨论的是一维情况,当使用二维平面内的周围多个站进行三角内插时,模型从曲线扩展为曲面,但误差产生原理相同。根据式(3),在有多个观测值时,待插值点的模型输出结果如下:
| $ \begin{gathered} n F\left(P_0\right)=\sum F\left(P_i\right)+\sum\left(P_0-P_i\right) \frac{\mathrm{d}}{\mathrm{d} P} F\left(P_i\right)+ \\ \sum\left(P_0-P_i\right)^2 \frac{\mathrm{d}^2}{\mathrm{~d}^2 P} F\left(P_i\right)+\cdots+\delta \end{gathered} $ | (4) |
引入周围更多的站点信息,可以估计出电离层的曲率变化,对应式(4)就是可以获得高阶的电离层变化率,因此,增加参考点的数量可以有效提高插值效果。同时考虑到电离层在地理经度和地磁经度方向上的规律性更强,可以更好地符合数学规律表达,本文提出了一种基于电离层线状变化特征的建模方法,通过选择在地理位置上具备一定特征的测站(同一地磁经度链或地理经度链),考虑电离层变化的高阶梯度,有效保证和提高了电离层内插的精度,同时降低了对测站间距的要求。采用动态定阶模型获得同一经度链上一系列测站的STEC变化的高阶梯度。对这一系列观测值进行了多项式拟合处理,并且使用不同阶数的多项式进行拟合,再将这些多项式中拟合误差最小的一个模型作为最终模型进行内插计算。
2 实验与分析 2.1 测站与时段选取本文选取了一系列处于同一地理经度链、地理纬度链和地磁经度链中的多个站点数据进行分析,相邻站点间距100 km左右。所选测站位于北美大陆,其中,地磁经度带所选内测站位于地磁经线57.5°W两侧,地理经度带内所选测站位于地理经线119°W左右,地理纬度带内所选测站位于地理纬线39°N线附近。为了检验本文方法在不同季节因素影响下的效果,选取了太阳活动较强的2014年两分两至(春分3月21日,夏至6月21日,秋分9月23日,冬至12月22日)前后7天(共28天),每天当地时间上午8时,中午14时与下午18时3个时段各2 h的数据进行比较。同时,为了和面状建模方法进行比较,选取了距待插值站点(P672)100 km左右的8个站点(P736、P784、P661、P730、P731、P348、P670、mdmt)进行电离层面状建模。
2.2 原始数据计算基于GNSS原始数据,首先对数据进行预处理,包括周跳和粗差探测等,再对预处理后的文件进行处理,估计GNSS信号传播过程中的电离层延迟,再推算出GNSS信号传播路径中的电离层电子含量:
| $ T_e=\frac{f_1^2 f_2^2}{40.28\left(f_1^2-f_2^2\right)}\left[L_4-\left\langle P_4+L_4\right\rangle_{\mathrm{arc}}+c\left(B_r+B^s\right)\right] $ | (5) |
式中,f1和f2表示GNSS信号中L1波段和L2波段的频率,分别为1 575.42 MHz和1 227.60 MHz;P4和L4为码和载波相位在L1波段和L2波段的频率之间形成的无几何组合观测量;〈P4 + L4〉arc为在连续弧段中相位平滑伪距的均值;Br和Bs为硬件延迟,即预处理过程中计算的差分码偏差(differential code bias,DCB)值。
通过获取信号路径上的STEC,对应穿刺点坐标可以由站坐标和卫星坐标计算得到。后续根据观测时间和具有相同PRN的卫星信号记录进行分类,得到同一时间各个站点对同一卫星的观测结果。同时,为了排除接收机和卫星的DCB带来的误差,先利用参与计算的基站及其周围站点来估计接收机和卫星的硬件延迟DCB[14],在后续计算过程中将会剔除其影响。
2.3 结果分析图 1展示了2014年利用3种线状建模和一种面状建模分别进行内插得到的误差均值和标准差,可以发现,在上午(地方时8时)、中午(地方时14时)和下午(地方时18时)3个时段,使用沿地磁经线和地理经线排列的测站所建模型的插值结果多优于沿地理纬线建模的结果,同时在全天大部分时间面状建模的结果比线状建模结果差。
 |
| 图 1 不同季节、不同时刻和不同测站分布对插值结果的影响 Fig.1 Effect of Different Seasons, Different Times and Different Station Distributions on Interpolation Results |
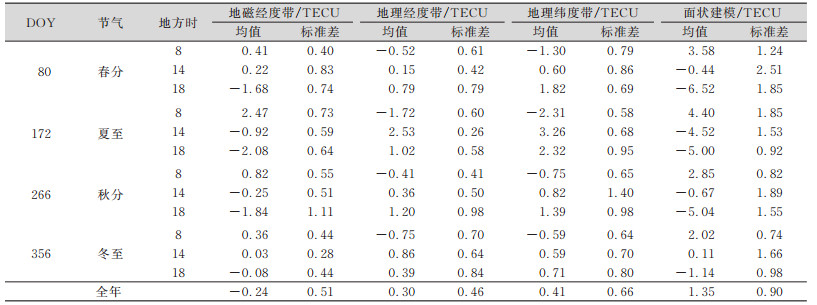
线状建模插值误差统计结果见表 1,在电离层较为活跃的DOY172地方时14时,线状建模误差均值和标准差的最优结果分别为-0.92 TECU和0.26 TECU,面状建模误差均值和标准差分别约为线状建模误差均值和标准差的最优结果的4. 9倍、5.9倍;使用地磁经度带和地理经度带内的测站数据得到的误差均值和标准差的最优结果分别为-0.92 TECU和0.26 TECU,相较于地理纬度带的结果,误差均值减小了72%,标准差减小了62%;2014年整年,相比面状建模误差均值和标准差,线状建模误差均值和标准差的最优结果分别减小了82% 和49%。
| 表 1 地方时8时、14时、18时的插值误差 Tab.1 Interpolation Errors at Local Time 8:00, 14:00 and 18:00 |
 |
为解释表 1中在DOY80地方时18时,地理纬度带的标准差优于地磁经度和地理经度的标准差,图 2给出了部分STEC结果对比序列,图 2(a)为DOY80地方时18时GPS系统中PRN为9的卫星在5个时刻的穿刺点处的STEC值,其中,地磁经度带和地理经度带内的测站观测卫星的穿刺点依纬度大小排序,地理纬度内的测站观测卫星的穿刺点依经度大小排序;图 2(b)为DOY80地方时8时GPS系统中PRN为14的卫星在5个时刻的穿刺点处的STEC值,穿刺点排列规则与图 2(a)相同。在地方时18时,3种测站分布情况下,卫星穿刺点STEC序列未见太多规律性,而地方时8时的序列中沿地理经线和地磁经线排列的STEC序列有明显的变化趋势。这种区别导致在地方时18时,利用3种模型拟合得到的结果均较地方时8时的差。
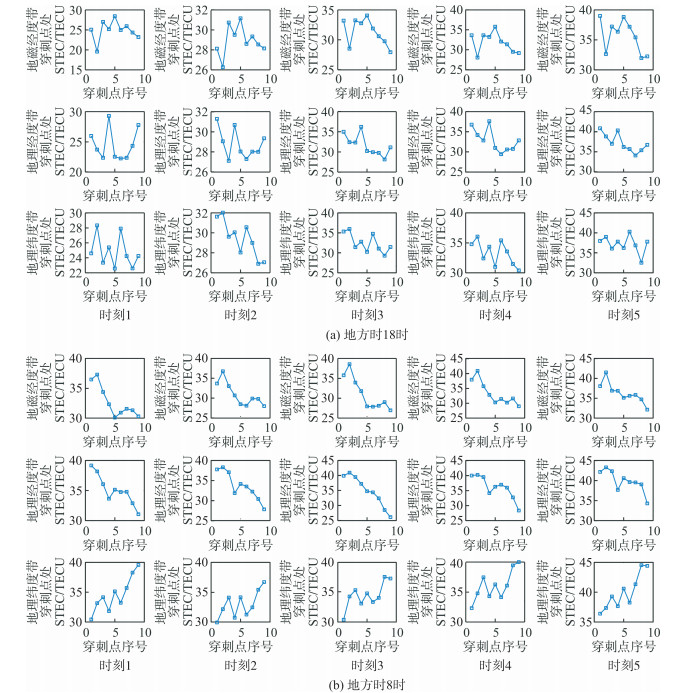 |
| 图 2 不同地方时的插值效果 Fig.2 Interpolation Effect at Different Local Times |
3 结束语
基于电离层线性变化特征规律性强的特点,本文通过选择具备一定地理位置约束条件的站点进行电离层建模。选择处于北美大陆中纬度地区的一系列沿地磁经线、地理经线和地理纬线分布的站点进行建模分析,同时将结果与同一区域面状建模结果进行比对。利用多项式拟合插值算法对以上4种分布的站点进行内插分析,使用沿地理经线或地磁经线分布的站点数据进行建模得到的模型误差较小,在DOY172地方时14时,面状建模误差均值和标准差分别约为线状建模误差均值和标准差的最优结果的4.9倍、5.9倍;相较于地理纬度带的结果,地磁经度带和地理经度带误差均值和标准差的最优结果分别减小了72%、62%;2014年整年,相比面状建模误差均值和标准差,线状建模误差均值和标准差的最优结果分别减小了82% 和49%。从以上结果来看,扩大站间距到100 km后,使用有地理位置约束的线状建模方式优于传统的面状建模方式。另一方面,在不同时间的比较中发现,使用本文模型在一年中夏季的建模效果较其他季节差。此外,该模型在其他地区和纬度带的适用性正在验证中,将在进一步的研究中逐步完善。
| [1] |
杨力. 大气对GPS测量影响的理论与研究[D]. 郑州: 信息工程大学, 2001
|
| [2] |
Colombo O L, Hernandez-Pajares M, Juan J M, et al. Wide-Area, Carrier-Phase Ambiguity Resolution Using a Tomographic Model of the Ionosphere[J]. Navigation, 2002, 49(1): 61-69. DOI:10.1002/j.2161-4296.2002.tb00255.x |
| [3] |
Øvstedal O. Absolute Positioning with Single-Frequency GPS Receivers[J]. GPS Solutions, 2002, 5(4): 33-44. DOI:10.1007/PL00012910 |
| [4] |
Basu S, MacKenzie E, Basu S. Ionospheric Constraints on VHF/UHF Communications Links During Solar Maximum and Minimum Periods[J]. Radio Science, 1988, 23(3): 363-378. DOI:10.1029/RS023i003p00363 |
| [5] |
Olatunbosun L, Ariyibi E A, Olabode O A, et al. Investigation of Scintillation Occurrence During Intense Geomagnetic Storms at Low Latitude Stations[J]. Physics & Astronomy International Journal, 2017, 1(1): 32-37. DOI:10.3969/j.issn.1005-202X.2017.01.007 |
| [6] |
Klobuchar J A. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users[J]. IEEE Transactions on Aerospace and Electronic Systems, 1987, AES-23(3): 325-331. DOI:10.1109/TAES.1987.310829 |
| [7] |
Themens D R, Jayachandran P T. Solar Activity Variability in the IRI at High Latitudes: Comparisons with GPS Total Electron Content[J]. Journal of Geophysical Research: Space Physics, 2016, 121(4): 3793-3807. DOI:10.1002/2016JA022664 |
| [8] |
Okoh D, Onwuneme S, Seemala G, et al. Assessment of the NeQuick-2 and IRI-Plas 2017 Models Using Global and Long-Term GNSS Measurements[J]. Journal of Atmospheric and Solar-Terrestrial Physics, 2018, 170: 1-10. DOI:10.1016/j.jastp.2018.02.006 |
| [9] |
Sandro M. The NeQuick Model Genesis, Uses and Evolution[J]. Annals of Geophysics, 2009, 52(3/4): 417-422. |
| [10] |
朱永兴, 谭述森, 杜兰, 等. 顾及粗差影响的全球电离层克里金插值及精度分析[J]. 测绘学报, 2019, 48(7): 840-848. |
| [11] |
柳景斌, 王泽民, 王海军, 等. 利用球冠谐分析方法和GPS数据建立中国区域电离层TEC模型[J]. 武汉大学学报·信息科学版, 2008, 33(8): 792-795. |
| [12] |
朱永兴, 谭述森, 明锋, 等. 顾及经纬度方向异性的电离层TEC IDW插值及精度分析[J]. 武汉大学学报·信息科学版, 2019, 44(11): 1605-1612. |
| [13] |
韩吉德, 王祖顺, 王春青. 全球电离层时空变化特性分析[J]. 测绘地理信息, 2012, 37(6): 26-29. |
| [14] |
章红平, 施闯, 唐卫明. 地基GPS区域电离层多项式模型与硬件延迟统一解算分析[J]. 武汉大学学报·信息科学版, 2008, 33(8): 805-809. |
 2022, Vol. 47
2022, Vol. 47

