| 大气可降水量与实际降水量的关联性分析 |
降水是一种重要的天气现象,降水会对人们的生活产生重要的影响,尤其是暴雨天气,不光会影响人们的生活,还会造成经济损失,所以能够实时监测和预报降水具有重要意义[1]。水汽是形成降水的重要条件,空气中充足的水汽含量是降水发生的先决条件。空气中水汽含量的突然变化往往会带来降水。传统探测水汽多采用无线电探空仪和水汽辐射计,或者采用卫星遥感与激光雷达的方法。然而传统的探测手段具有很多局限性,难以获得高空间和时间分辨率的水汽信息[2]。GPS (global positioning system)气象学成为弥补上述缺陷的一个有效方法,其基本过程是根据观测数据解算对流层天顶总延迟ZTD (zenith total delay),然后分离出天顶静力延迟ZHD (zenith hydrostatic delay),ZTD与ZHD之差即为对流层天顶湿延迟ZWD (zenith wet delay),再通过ZWD与PWV之间的关系计算得到PWV[3]。要研究PWV与实际降水量之间的关系,获得高精度的水汽含量是至关重要的。相关的研究已经表明,不论是采用GPS差分技术还是精密单点定位PPP (precise point positioning)技术,当ZTD的解算精度小于6 mm时,均可以得到近似精度约为1 mm的水汽含量,与水汽辐射计和探空资料获得的水汽精度是基本相当的,因此用地基GPS技术遥感大气水汽含量是可行的[3]。
本文主要分析研究PWV与实际降水量之间的关联性。利用PPP技术估计出IGS武汉站上空的PWV,采用的数据主要是2012年街道口洪山站的降雨量与2012年IGS武汉站的观测数据,分析PWV与实际降雨之间的关系,为降水预报尤其是暴雨预报提供参考。
1 PWV的计算 1.1 利用无线电探空资料计算PWV根据PWV的定义有[4]:
| $ {\rm{PWV}} = \frac{1}{{{\rho _{{\rm{water}}}}}}\int_0^H {{\rho _\mathit{w}}{\rm{d}}z} = \frac{1}{{{\rho _{{\rm{water}}}}}}\int_0^H {\frac{{{\rho _w}}}{\rho }\frac{1}{g}{\rm{d}}p} = \frac{1}{{{\rho _{{\rm{water}}}}}}\int_0^p {\frac{q}{g}{\rm{d}}p} $ | (1) |
式中,ρwater为液态水的密度;ρw为大气中水汽的密度;ρ为大气密度;H为高度;g为重力加速度;P为气压;q为比湿。利用探空资料获得的观测数据,利用公式(1)即可求得测站上空的PWV。
1.2 基于PPP技术的PWV的计算PPP技术是利用IGS公布的精密星历和钟差文件,通过线性组合消除一阶电离层延迟,经验模型消除ZHD及其他误差项,经过数据处理:粗差探测及剔除、周跳探测,并将ZWD随同其他未知参数利用卡尔曼滤波一起估计,经过一段时间的收敛以后,即可获得稳定的对流层参数估计。
ZHD主要是指由干大气引起的延迟在天顶方向的投影,由于干大气较为符合理想气体方程和静力学平衡方程,因而可以用理论模型公式进行计算。本文使用的是Saastamoinen模型,该模型只需要知道测站的坐标以及气压即可求解ZHD[5]。公式如下:
| $ \Delta L_h^0 = {\rm{ZHD = }}\frac{{2.2779 \pm 0.0024{P_s}}}{{f\left( {\mathit{\lambda }, H} \right)}} $ | (2) |
式中,Ps为地表总气压;
| $ f\left( {\lambda, H} \right) = 1 - 0.00266\cos 2\lambda - 0.00028H $ | (3) |
其中,λ为测站的纬度;H为测站的大地高。
所以在本文地基GPS遥感水汽时,通过获取IGS武汉站的气压,利用经验模型计算得到ZHD,采用ZTD减去ZHD即可获得ZWD。
PWV与ZWD有如下函数关系:
| $ {\rm{PWV}} = {\rm{\Pi }} \cdot \Delta {L_w} $ | (4) |
式中,Π是无量纲的水汽转换系数,有如下表达式:
| $ {\rm{\Pi }} = \frac{{{{10}^6}}}{{{\rho _w}{R_v}\left[{\frac{{{k_3}}}{{{T_m}}} + {k_2}'} \right]}} $ | (5) |
其中,
| $ {k_2}' = {k_2} - \frac{{{k_1}{M_W}}}{{{M_d}}} $ | (6) |
Rv为气体常数;k′2和k3为大气折射率常数;Tm就是对流层大气加权平均温度,也是ZWD转换成PWV的关键参数变量。常用的大气加权平均温度Tm的计算方法有基于大气廓线信息的计算方法、基于线性回归公式的计算方法,以及采用全球加权平均温度模型进行计算的方法。本文使用的是姚宜斌等构建的一个基于测站三维坐标及年积日的最新全球加权平均温度模型--GTm-Ⅲ模型[6]。该模型是目前最优的全球加权平均温度计算模型,且不需要实测地面温度,对计算PWV提供了方便和高精度的结果,保障了研究的可靠性。
1.3 GPS计算PWV与无线电探空资料计算PWV的比较无线电探空仪探测水汽技术能够提供水汽压、温度等相关资料,利用无线电探空仪探测水汽是气象部门探测大气水汽的常用方法,具有相当高的精度水平,常作为新方法的检验标准[7, 8]。为了检验由地基GPS对流层延迟推算PWV的精度,选择2012年的观测数据,由年积日160~240天的GPS观测数据计算PWV,绘制在图上,并使用无线电探空数据获得对应时间的PWV,比较两者之间的关系,并进行相关统计量计算。
图 1中,红色曲线代表由GPS数据推算的PWV,蓝色曲线代表的是由探空数据获得的相应时间的PWV。由图可知,两者之间的变化趋势基本是一致的,它们之间的差值的均值、相关系数、均方根等统计量如表 1所示。
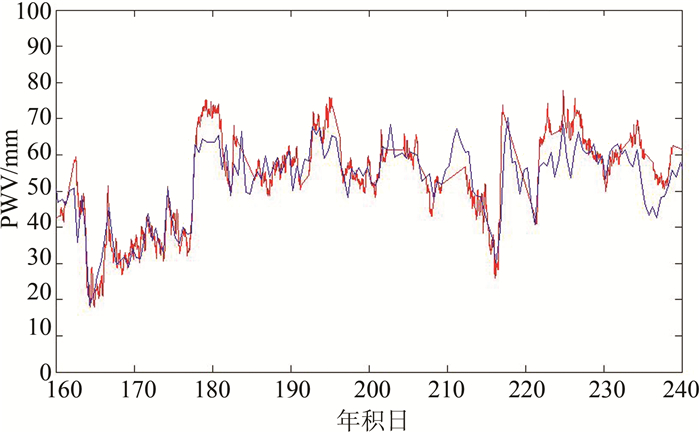 |
| 图 1 无线电探空数据与GPS数据计算可降水量比较 Figure 1 Comparison of PWV Between Radiosonde and GPS |
| 表 1 武汉站GPS计算PWV与探空数据计算可降水量的比较 Table 1 Comparison of PWV Between Radiosonde and GPS in Site WUHN |
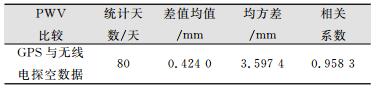 |
由于IGS武汉站与武汉无线电探空站并不完全处在一个位置,所以出现了在绝大部分时间是相当吻合、部分时间出现了偏差的现象。差值均值达到0.424 0 mm,主要的原因还是因为两个测站不在同一位置,所以存在一定的偏差,但是,相关系数也达到了0.958 3,说明用GPS观测数据推算PWV具有很高的精度,可以用于PWV的计算。
2 可降水量与实际降雨量的关联性分析 2.1 可降水量与降雨量整体相关性本文主要采用的是降水较多的夏季的数据,通过将水汽序列与降雨量序列在同一时间轴上对比分析可以发现,水汽与降雨量存在明显的相关性。从图 2中可以看出,降水多发生在水汽峰值出现的附近时期,且一般情况下,水汽增加的越剧烈,降雨量越大,水汽和降雨量之间存在很好的吻合。在年积日为180、195、226日3天,均发生了暴雨,水汽无一例外都出现了快速的增加,在相对较弱的降水出现之前,水汽一般也具有相对显著的突变发生。
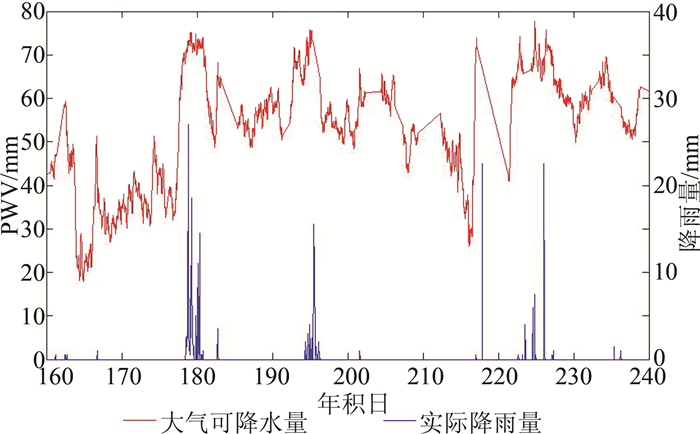 |
| 图 2 水汽与实际降雨对比分析 Figure 2 Comparison and Analysis Between PWV and Actual Rainfall |
2.2 水汽与该站暴雨发生时降雨量的比较
降水的形成有十分复杂的原因,所以小的降水就具有更大的随机性,与水汽的相关性也较弱。通常情况下,暴雨是指24 h内降水量在50~100 mm的降水。暴雨的形成必须要以充足的水汽作为先决条件,所以对暴雨时期水汽与降水序列进行分析具有更重要的意义。2012年街道口洪山站共发生5次暴雨,由于缺少观测数据,选取5月29日、6月27日、7月13日、8月13日4次降水进行分析。
从图 3中可以看出,每当暴雨发生时,暴雨的整个过程中水汽都处于较高的水平,4次过程水汽的最小值均大于60 mm,且并没有随着降雨的出现而很快的降低。这一结论也进一步说明,水汽是降水发生的先决条件,研究水汽与降水之间的关系是必要且有效的。
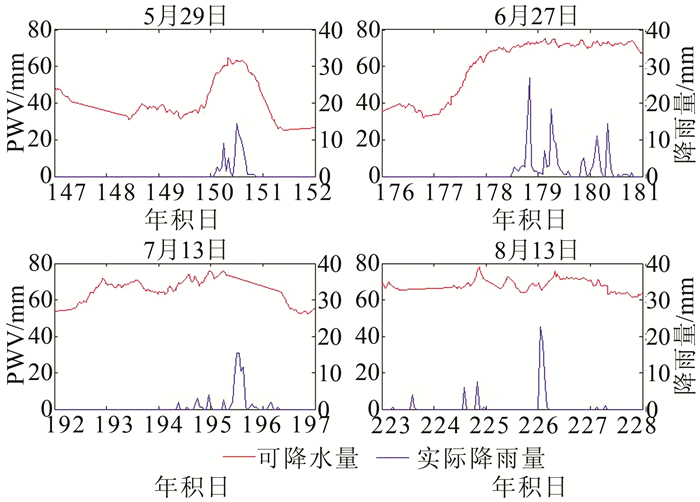 |
| 图 3 2012年4次暴雨分析 Figure 3 Analysis of 4 Storms in 2012 |
2.3 水汽突变与暴雨预报
虽然暴雨的发生需要有充足的水汽为基础,但是研究暴雨预报前兆,更重要的是要了解暴雨发生前大气可降水量的特征,并能进行暴雨预报。短临预报是指对未来0~3 h天气的预报。暴雨短临预报是指在暴雨发生0~3 h之前,对暴雨的发生进行预测。在暴雨发生之前,水汽一般会出现一个相对大的突变,水汽的突变量与当前水汽的水平有一定关系,如果当前水汽已经处在一个高值,水汽增量会相对较小,如果当前水汽处在相对低值,水汽的增量会比较大,但不论哪种情况,水汽增量相对于周围增量序列都必然可以看作是一个突变,也即可以作为暴雨预测的一个指标。
以2012年两次日降雨量超过70 mm的序列进行分析。2012年5月29日发生的暴雨如图 4所示,水汽从0时开始一直处于缓慢增加状态,20时左右水汽出现一个约4 mm/5 min的激增,紧接着22时暴雨开始出现,直到24时降水量达到峰值,随后大气可降水量才开始缓慢降低,当日的降水总量为77 mm。2012年6月27日发生的暴雨如图 5所示,水汽开始处于小幅震荡状态,8时左右,水汽出现了一个相对大的激增,大约是1.5 mm/5 min左右,随后约11时左右降水开始出现,也即是该日暴雨的开端,当天的降雨总量达到了71.5 mm。
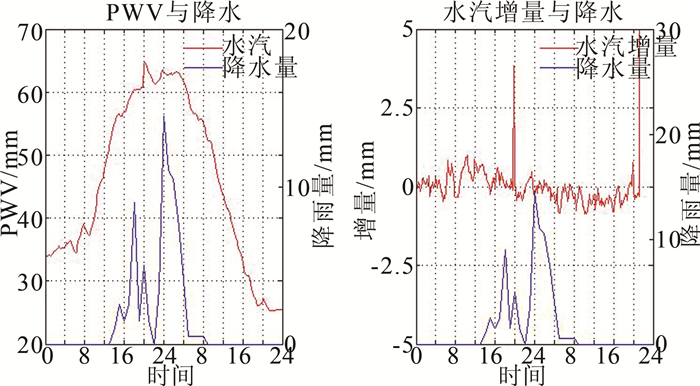 |
| 图 4 5月29日水汽含量、水汽增量与降水分布对比图 Figure 4 Comparison of PWV, Increment of PWV and Actual Rainfall on May 29 |
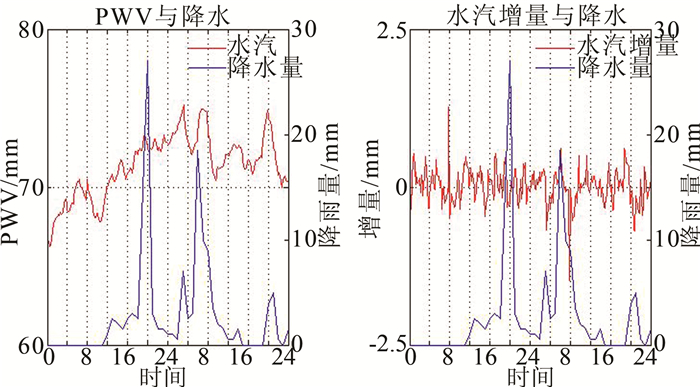 |
| 图 5 6月27日水汽含量、水汽增量与降水分布对比图 Figure 5 Comparison of PWV, Increment of PWV and Actual Rainfall on June 27 |
同时也可以看出,水汽增量峰值会和降雨量峰值出现一定的时间延迟,会超过4 h或者更多,这是因为:一方面,强对流天气中,雨水从高空降落到地面需要一定的时间;另一方面,GPS信号对液态水不如对水汽那么敏感。
也就是说,当水汽已经积累到一定的程度(60 mm左右),一个相对大的水汽突变,一般会在2~3 h左右之后发生暴雨,上述两个降雨增量序列都很好地说明了这一点,但是对有的序列而言,激增点可能会发生在降雨开始5 h之前甚至更早,然后水汽一直保持在一个较高的水平。但是也有研究已经表明,水汽的突增和突降都与暴雨的发生有关,也就是说,仅仅依靠水汽的增量还具有不确定性,只能作为暴雨发生的一个辅助性参考依据。
3 结束语本文深入研究了高精度大气可降水量的计算方法,同时对水汽与降雨量进行了关联性分析,可以肯定水汽与降水存在明显的关联性。借助武汉街道口洪山站的观测数据,着重分析了暴雨来临前水汽总量及增量特征,当水汽达到高值,一个明显的水汽含量激增往往会伴随暴雨的出现。总之,充足的水汽含量是暴雨发生的必要准备,在此基础上水汽的激增对暴雨的预报有一定的参考和指示作用,可以为目前现有的暴雨预报提供辅助信息,为研究水汽和更好的管理和利用水资源提供一定的参考[9, 10]。
| [1] |
李黎, 匡翠林, 朱建军, 等. 基于实时精密单点定位技术的暴雨短临预报[J].
地球物理学报,2012,55(4) : 1129–1136.
Li Li, Kuang Cuilin, Zhu Jianjun, et al. Rainstorm Nowcasting Based on GPS Real-Time Precise Point Positioning Technology[J]. Chinese Journal of Geophysics,2012,55(4) : 1129–1136. |
| [2] |
陈永奇, 刘焱雄, 王晓亚, 等. 香港实时GPS水汽监测系统的若干关键技术[J].
测绘学报,2007,36(1) : 9–12.
Chen Yongqi, Liu Yanxiong, Wang Xiaoya, et al. GPS Real-Time Estimation of Precipitable Water Vapor-Hong Kong Experiences[J]. Acta Geodaetica et Cartographica Sinica,2007,36(1) : 9–12. |
| [3] |
朱爽.地基GPS遥感大气可降水量研究[D].武汉:武汉大学, 2012 Zhu Shuang. Research of Remote Sensing Water Vapor Using Ground-Based GPS [D]. Wuhan: Wuhan University, 2012 |
| [4] |
金慧华, 白征东, 过静珺, 等. 地基GPS反演水汽影响因素分析[J].
测绘科学,2008,33(4) : 65–67.
Jin Huihua, Bai Zhengdong, Guo Jingjun, et al. The Analysis of Several Factors for the Ground-Based GPS Remote Sensing of Water Vapor[J]. Science of Surveying and Mapping,2008,33(4) : 65–67. |
| [5] |
甘桂琴, 邹峥嵘, 刘平. GPS测量中天顶干延迟的计算方法研究[J].
测绘与空间地理信息,2013,36(1) : 134–137.
Gan Guiqin, Zou Zhengrong, Liu Ping. Research on Method of Calculating Zenith Dry Delay in GPS Measurement[J]. Geomatics & Spatial Information Technology,2013,36(1) : 134–137. |
| [6] | Yao Y B, Xu C Q, Zhang B, et al. GTm-III: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapor[J]. Geophysical Journal International,2014,197(1) : 202–209. DOI:10.1093/gji/ggu008 |
| [7] |
王勇, 何荣, 杨彬云, 等. GPS反演的可降水量与降水的对比分析研究[J].
测绘科学,2010,35(5) : 80–82.
Wang Yong, He Rong, Yang Binyun, et al. Study of Comparisons Between GPS Precipitable Water Vapor and Rainfall[J]. Science of Surveying and Mapping,2010,35(5) : 80–82. |
| [8] |
王勇, 刘严萍, 柳林涛, 等. 区域GPS网对流层延迟直接推算可降水量的研究[J].
热带气象学报,2007,23(5) : 510–514.
Wang Yong, Liu Yanping, Liu Lintao, et al. The Study of Directly Calculating Precipitable Water Vapor with Zenith Tropospheric Delay of GPS Network[J]. Journal of Tropical Meteorology,2007,23(5) : 510–514. |
| [9] |
贺小星, 花向红, 周世健. GPS时间序列中异常周期信号影响机制分析[J].
测绘地理信息,2014,39(2) : 22–26.
He Xiaoxing, Hua Xianghong, Zhou Shijian. The Effects Mechanism of Anomalous Period Signal in GPS Time Series[J]. Journal of Geomatics,2014,39(2) : 22–26. |
| [10] |
陈俊勇. 地基GPS遥感大气水汽含量的误差分析[J].
测绘学报,1998,27(2) : 113–118.
Chen Junyong. On the Error Analysis for the Remote Ssensing of Atmospheric Water Vapor by Ground Based GPS[J]. Acta Geodaetica et Cartographica Sinica,1998,27(2) : 113–118. |
 2016, Vol. 41
2016, Vol. 41

