| 基于BAS-BP模型的深基坑开挖地表沉降预测 |
在城市化进程中,由于城市地表面积有限,地下和地上高空间逐渐被开发、利用起来,因此深基坑的数量规模和开挖深度逐渐增加[1, 2]。深基坑开挖必然会导致地面沉降和土体变形等环境问题,严重时甚至会导致周围建筑物倾斜和道路破坏。因此,对基坑周围地表沉降预报的及时性与精度要求越来越高[3]。
目前针对沉降数据的预测主要有时间序列分析[4]、灰色系统理论[5]和反向传播(back propagation,BP)神经网络[6]等方法。其中,BP神经网络因为自学习性强、自适应性好,可以完成复杂非线性映射而得到普遍运用。但BP神经网络存在收敛速度慢、容易过度拟合和陷入局部最优的问题,预测效果并不理想。为了提高BP神经网络对沉降预测的可靠性和预测精度,本文引入天牛须搜索(beetle antennae search,BAS)算法对BP神经网络的初始权值和阈值进行优化,建立BAS-BP预测模型。
1 BP神经网络及BAS算法 1.1 BP神经网络原理BP神经网络是一种依照逆向误差传播的多层前馈网络[7, 8],其组成结构由输入层、隐含层和输出层组成,BP神经网络模型训练步骤如下:
1)初始化神经网络,确定各层结构之间的权值及阈值。
2)计算隐含层输出Sj,只有输出信号与权值相乘之和满足当前神经元阈值才通过激活函数输出。
| $ S_j=f\left(\sum\limits_{i=1}^n w_{i j} x_i-a_j\right) $ | (1) |
式中,f(·)表示激活函数;wij表示第i个输入值与第j个神经元的权值;xi表示第i个输入值;aj表示隐含层第j个神经元阈值;n表示输入层神经元个数。
3)计算预测输出yk:
| $ $ | (2) |
式中,wjk表示隐含层第j个神经元与输出层第k个神经元的权值;bk表示输出层第k个神经元的阈值;q表示隐含层神经元个数。
4)运用误差反向传播计算新的权值及阈值。计算预测输出yk与期望输出Yk之间的误差,采用误差函数梯度下降的方式使整个网络的预测输出逐渐逼近期望输出,并且不断优化各层之间的权值和阈值,公式如下:
| $ \left\{\begin{array}{l} w_{i j}=w_{i j}+\eta S_j\left(1-S_j\right) x_i \sum\limits_{j=1}^q S_j w_{j k}\left(Y_k-y_k\right) \\ w_{j k}=w_{j k}+\eta\left(1-S_j\right)\left(Y_k-y_k\right) \end{array}\right. $ | (3) |
| $ \left\{\begin{array}{l} a_j=a_j+\eta S_j\left(1-S_j\right) \sum\limits_{j=1}^q w_{j k}\left(Y_k-y_k\right) \\ b_k=b_k+\left(Y_k-y_k\right) \end{array}\right. $ | (4) |
式中,η表示学习效率
根据以上步骤迭代往复至yk与Yk的误差小于已设定误差或达到终止训练次数后停止学习,将预测样本向量代入式(1)、式(2)即可得到预测值。
1.2 BAS算法BAS算法是一种根据天牛觅食原理开发的仿生式智能优化算法[9, 10]。其仿生原理如下:天牛寻找食物时,通过两根触须不断搜寻食物气味,根据搜寻到的气味的强度调整移动方向,即左边触须接受的食物气味大向左移动,反之则向右移动。由此可以假定一个任意形式的函数就是食物气味,天牛两个触须不断采集自身周围两点的气味值,即不断比较两个适应度函数值的大小,最终找到全局气味值最大的点,这时就完成了高效的函数寻优[11, 12]。目前,已有学者建立了BAS-BP模型对风暴潮灾害损失数据进行预测分析[13];也有学者建立了基于BAS-BP神经网络的电缆阻水性评价模型[14],并证明该模型可有效评估电缆阻水性。
2 BAS-BP模型BP神经网络初始权值和阈值的确定对训练结果有很大影响,因此利用BAS算法对BP神经网络的权值和阈值进行寻优处理,并将寻优结果放到训练好的网络,构造出最终的BAS-BP神经网络模型。假定模型为M-N-P,M、N、P分别为输入层、隐含层、输出层的神经元数量,空间维度k = MN + NP + N + P,模型构建步骤如下:
1)创建代表天牛须方向的k维随机向量a = rands(k,1),并对向量进行归一化处理:
| $ \boldsymbol{b}=\frac{\operatorname{rands}(k, 1)}{\|\operatorname{rands}(k, 1)\|} $ | (5) |
式中,rands(·)表示随机函数。
2)建立天牛左右须空间坐标:
| $ \left\{\begin{array}{l} x_l^t=x^t+\frac{d_0 \boldsymbol{b}}{2} \\ x_r^t=x^t-\frac{d_0 \boldsymbol{b}}{2} \end{array}\right. $ | (6) |
式中,xlt表示第t次迭代时的左须坐标;xrt表示第t次迭代时的右须坐标;xt表示第t次迭代时的天牛质心坐标;d0表示两须之间的距离。
3)判断左右须气味强度,即F (xl)和F (xr)的强度,以更新天牛坐标。其中,F (·)为适应度函数。
| $ x^{t+1}=x^t-\theta^t \boldsymbol{b} \operatorname{sign}\left(F\left(x_l^t\right)-F\left(x_r^t\right)\right) $ | (7) |
式中,xt + 1表示第t + 1次迭代时的质心坐标;xt、xlt、xrt分别表示第t次迭代时的质心和左右须坐标;θt表示第t次迭代时的步长因子;F (xlt)、F (xrt)分别表示第t次迭代时左右须适应度函数。
4)设置步长因子。由于步长因子可以控制天牛的区域搜索能力,因此初始步长设置应尽可能大,最好与自变量最大长度相当,能够覆盖当前的搜索区域而不至于陷入局部最优值。令初始步长因子为θ,则第t + 1次步长可表示为:
| $ \theta^{t+1}=\theta^t \lambda $ | (8) |
式中,λ表示步长衰减因子,通常取λ = 0.95。
5)建立适应度函数。以均方误差(mean square error,MSE)作为适应度评价函数:
| $ F=\frac{1}{m} \sum\limits_{i=1}^m\left(y_i-Y_i\right)^2 $ | (9) |
式中,m表示训练样本数量;yi表示第i个训练样本的输出值;Yi表示第i个训练样本的实际值。
6)天牛位置初始化。随机给定天牛的初始位置,计算其适应度函数值,并保存在bestX,bestY中。其中,bestX为最佳的天牛初始位置,bestY为天牛初始位置的最佳适应度函数值。
7)按照式(6)更新天牛左右须位置坐标,并求出两须的适应度函数,对比两者强度大小,按照式(7)调整训练网络的权值和阈值,并计算在当前位置下的适应度函数值,若适应度函数值优于bestY,则更新bestX和bestY。
8)判断迭代是否达到最大次数,适应度函数值是否满足设定精度,预设条件满足时算法运行结束,否则重复步骤6)。将迭代停止后获得的bestX中的解作为权值和阈值最优解代入BP神经网络中进行二次学习,最终形成BAS-BP神经网络模型。
3 BAS-BP神经网络沉降预测模型 3.1 实验数据本文对深圳市某栋立体车库监测数据进行仿真实验。该工程开挖深度约为10 m,基坑开挖面积约为21 000 m2。依据现行的《建筑基坑工程监测技术规范》GB50497—2009、《建筑基坑支护技术规程》 JGJ120—99等有关规定,该基坑工程属于二级基坑工程,共布设沉降观测点31个,采用二等水准测量规范进行了50次沉降位移监测。本文选取C20号监测点进行实验,图 1展示了50期沉降监测数据的变化趋势。可以看出,从第33期开始沉降逐渐趋于稳定。因此本文选取前27期沉降数据作为训练样本构建神经网络沉降预测模型,对第28~32期累计沉降量进行预测。
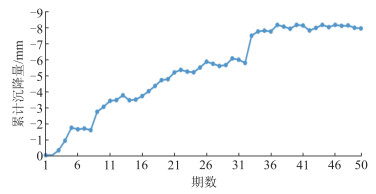 |
| 图 1 沉降监测数据变化趋势 Fig.1 Trend of Settlement Monitoring Data |
3.2 实验及结果分析
本文将前27期数据作为训练样本滚动式[15]预测第28~32期数据,即每连续5期数据为一组作为输入样本,接下来1期数据为期望输出,以此类推,分成22组训练样本。用训练好的BAS-BP神经网络预测后5期累计沉降,对比预测值与实测值,并分析预测精度。预测精度评价指标为平均绝对百分比误差(mean absolute percentage error,MAPE)、MSE和平均绝对误差(mean absolute error,MAE)。
本文实验中输入层有5个神经元,输出层有1个神经元,采用单隐含层设置,根据经验公式
BP神经网络和BAS-BP预测模型的训练样本拟合结果见图 2,可以看出,优化后的BAS-BP预测模型比BP网络精度更高,沉降量走势曲线更接近真实值,但有一处两种模型的拟合误差均较大,这是因为在进行沉降监测时,降雨、大风、支护等因素会使监测结果产生噪声,导致沉降曲线发生突变,因此预测模型进行预测拟合时噪声部分的精度有所降低[16]。两种模型拟合值与真实值的误差见表 1。
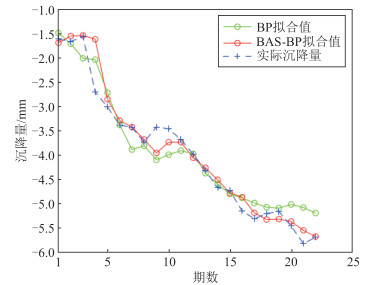 |
| 图 2 训练集拟合趋势 Fig.2 Fitting Trend of Training Set |
| 表 1 拟合值误差 Tab.1 Errors of Fitting Values |
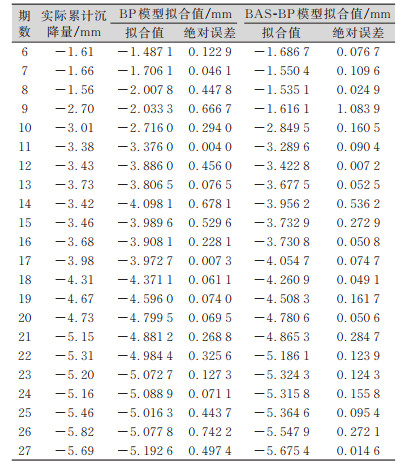 |
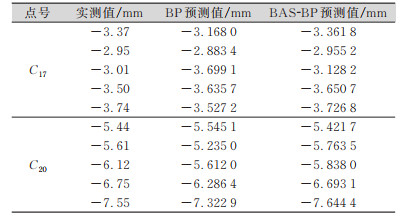
根据表 1数据进行计算,BP算法的MSE为0.37,相关性系数为0.92,BAS-BP算法的MSE为0.29,相关性系数为0.96,BAS-BP神经网络拟合值精度更高。为了检验BAS-BP算法的可靠性,避免预测结果的偶然性,本文另外选取C17点进行仿真预测,结果见表 2,并用MSE、MAE、MAPE对预测精度进行评价,结果见表 3。BAS-BP模型在两个监测点的预测精度均高于BP神经网络模型。根据表 3中的数据进行计算,发现相较于BP模型预测结果,C17点BAS-BP模型预测结果的MSE、MAE、MAPE分别提高了74.84%、77.37%、76.55%,C20点BAS-BP模型预测结果的MSE、MAE、MAPE则分别提高了58.66%、63.97%、65.38%。
| 表 2 C17、C20监测点的预测结果 Tab.2 Prediction Results of Monitoring Points C17 and C20 |
 |
| 表 3 模型预测精度 Tab.3 Prediction Accuracy of the Model |
 |
4 结束语
本文利用已有监测数据,使用BAS算法优化BP神经网络,建立了BAS-BP模型,对深基坑开挖引起的周围地表沉降效应进行了预测。分析可知,C17、C20点的BAS-BP模型预测结果优于BP模型结果。BAS-BP模型可提高预测精度,具有很好的鲁棒性和稳定性,预测精度可以满足基坑开挖引起周围地表沉降效应的监测要求。此外,数据噪声会引起监测曲线的突变,降低预测精度,因此采用小波变换等方法对数据信号进行降噪处理可以有效避免个别数据导致的监测曲线突变,扩大预测模型的适用范围。
| [1] |
孟雪, 赵燕容, 黄小红, 等. 基于灰色GM(1, 1)和神经网络组合模型的基坑周边地面沉降预测分析[J]. 勘察科学技术, 2018(6): 39-44. DOI:10.3969/j.issn.1001-3946.2018.06.009 |
| [2] |
宋楚平. 一种改进的BP神经网络深基坑变形预测方法[J]. 土木工程与管理学报, 2019, 36(5): 45-49. DOI:10.3969/j.issn.2095-0985.2019.05.008 |
| [3] |
周星勇, 杨容浩, 王志胜, 等. 一种改进遗传神经网络的建筑基坑沉降预测模型[J]. 测绘工程, 2018, 27(3): 53-57. |
| [4] |
徐爱功, 李娜, 张涛. 时间序列分析在地铁沉降观测中的应用[J]. 测绘科学, 2013, 38(5): 57-60. |
| [5] |
李小刚, 张廷会. GM(1, 1)灰色预测模型在道路软基沉降预测中的应用[J]. 铁道科学与工程学报, 2016, 13(1): 63-68. DOI:10.3969/j.issn.1672-7029.2016.01.010 |
| [6] |
Lu F M, Li J. Application of Kalman Filter Method Based on Water Level Factors in the Dam Deformation Forecast[J]. Advanced Materials Research, 2013, 648: 376-380. DOI:10.4028/www.scientific.net/AMR.648.376 |
| [7] |
张彬. 融合遗传算法和BP神经网络对基坑地表沉降预测的应用研究[J]. 北京测绘, 2018, 32(10): 1 152-1 155. |
| [8] |
赵祥鸿, 暴景阳, 欧阳永忠, 等. 利用BP神经网络剔除多波束测深数据粗差[J]. 武汉大学学报·信息科学版, 2019, 44(4): 518-524. |
| [9] |
Jiang X Y, Li S. BAS: Beetle Antennae Search Algorithm for Optimization Problems[J]. International Journal of Robotics and Control, 2018, 1(1): 1. DOI:10.5430/ijrc.v1n1p1 |
| [10] |
Jiang X Y, Li S. Beetle Antennae Search Without Parameter Tuning(BAS-WPT)for Multi-objective Optimization[EB/OL]. [2020-01-15]. https://arxiv.org/abs/1711.02395
|
| [11] |
温静媛, 苗鸿宾, 刘晓峰. 基于BAS-BP的深孔加工粗糙度的预测[J]. 机械设计与研究, 2019, 35(5): 80-83. |
| [12] |
刘晓峰, 苗鸿宾, 温静媛. 基于BAS-BP神经网络的钻削力预测[J]. 组合机床与自动化加工技术, 2019(8): 49-52. |
| [13] |
王甜甜, 刘强. 基于BAS-BP模型的风暴潮灾害损失预测[J]. 海洋环境科学, 2018, 37(3): 457-463. |
| [14] |
陈馨凝, 刘辉, 刘雨薇, 等. 基于BAS-BP模型的电缆阻水性评估研究[J]. 湖北工业大学学报, 2019, 34(4): 35-39. |
| [15] |
冯绍权, 花向红, 陶武勇, 等. 一种基于GA-BP-MC神经网络的高铁桥墩沉降预测模型[J]. 测绘通报, 2019(7): 50-53. |
| [16] |
郑云云, 陈姗姗, 胡勇. 小波变换和BP神经网络模型在沉降变形监测中的应用研究[J]. 测绘与空间地理信息, 2019, 42(2): 101-103. |
 2022, Vol. 47
2022, Vol. 47


