| 利用低频浮动车交叉口运行状态的单车路段行程时间估计 |
2. 武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉,430079;
3. 华为技术有限公司,广东 深圳,518129
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Huawei Technologies Co., Ltd., Shenzhen 518129, China
单车路段行程时间估计是交通分析的基础,估计的准确度影响路段平均行程时间计算、路段行程时间预测以及基于大数据的路段行程时间统计规律的研究。因此,如何采用有效的方法准确估计单车路段行程时间已成为国内外研究的热点。国际上对单车路段行程时间的估计一般采用线圈检测数据[1]和浮动车数据,其中,利用GPS信息对路段行程时间进行估计在国外已经开展[2-5]。在国内,利用丰富的浮动车GPS信息估计路段行程时间方面的研究业已开展[6-8],但大量的研究工作是针对理想的高频采样数据。目前,基于GPS信息估计单车路段行程时间的方法中,对浮动车在路段交叉口区域运行状态的处理过于简单,传统的基于运行时刻数据的时间插值法[9]大多假设车辆在交叉口区域匀速行驶,对路段端点通过时刻进行插值,将交叉口处的等待时间平均分配到路段上,GPS采样频率越高,产生的误差越小,但对于低频GPS数据会产生较大误差;于德新等[10]考虑车辆运行状态并给出了计算路段边界点通过时间的方法,但将车辆在交叉口区域内与交叉口区域外的运行状态混淆,并且当GPS点在定位偏差圆内计算路段入口通过时刻时包含了本应忽略的等待时间,导致对路段单车行程时间估计不准确。鉴于此,本文对车辆在交叉口区域内外的运行状态进行了分析,并对不能真实反映路段交通流运行特性的单车路段行程时间予以剔除,进一步提高单车路段行程时间估计的准确性。
1 基于概率转换的地图匹配方法由于GPS系统存在定位误差,城市路网自身也存在误差,加之其他因素影响如城市建筑对GPS信号的遮挡、定位信号丢失等造成的误差,使得浮动车GPS轨迹点偏离车辆实际运行的道路[11]。在车辆导航、路段或路径行程时间计算、行程时间预测以及路径规划中,需要通过一定的方法将偏离真实道路的GPS点纠正到车辆真实运行的道路上,实现GPS与GIS数据的融合,实现地图匹配[12]。对单车路段行程时间的计算就是利用这些经过纠正的GPS点信息来进行的,因此地图匹配是影响估计路段行程时间准确性的一个关键环节。
1.1 数据预处理1) GPS原始数据以及路网数据预处理。GPS接收机记录的数据经常存在异常数据,如经纬度坐标为0的数据,在数据入库的过程中要把这些异常点去掉,并在数据库中构建索引。
2) 路网拓扑、连通关系构建。根据路网间节点与线的连接关系,构建点线拓扑关系,以保证在路径选取中断时,在两GPS点间进行最短路径拟合。利用道路扩展级别来度量道路间存在的连通关系[11]。本文使用的浮动车数据采样平均时间间隔为40 s,构建路段间三级连通集合即可满足地图匹配的要求。路段之间的连通性如图 1所示。
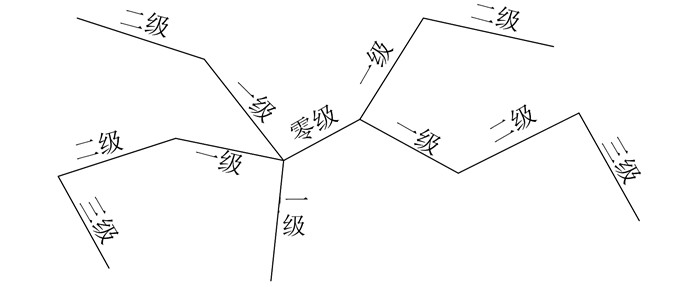 |
| 图 1 路段三级连通集合 Fig.1 Three-Level Connection Set |
1.2 候选道路评分计算
1) 筛选候选道路集合。候选道路集合为GPS轨迹点的可能道路集合,GPS点与路段的距离越小,该路段越有可能是浮动车的轨迹路段,因此通过路段与GPS点的距离初步判断可能为GPS轨迹的路段。距离GPS点pi一定范围(r)内的路段ei, 如满足条件d(pi, ei)≤r,则这样的路段为GPS点的可能轨迹路段,所有路段的集合称为候选道路集,表示为{ei|d(pi, ei)≤r}。
对于距离有如下定义:当GPS点与待匹配路段间只有一个投影点时,则距离为GPS点到待匹配路段上投影点的距离;有多个投影点时,距离为GPS点运动方向与待匹配路段方向夹角最小的路段投影点之间的距离;没有投影点时,距离为GPS点到路段两端点间距离的最小值。因此,GPS点与路段的距离可表示为:
| $ d\left( {Q, AB} \right) = \left\{ \begin{array}{l} d\left( {Q, Q'} \right), Q' \in AB\\ \min \left\{ {d\left( {Q, A} \right), d{\rm{ }}\left( {Q, B} \right)} \right\}, 其他 \end{array} \right. $ | (1) |
式中,Q表示GPS点;AB表示待匹配路段;Q′表示Q点在AB上的投影点。
2) 候选道路综合评分。根据GPS点的候选道路集合,对集合中的每一条道路采用基于权重的方法打分,候选道路综合评分W包括距离评分Wd和方向评分Wa,即W=Wa+Wd。综合评分越高,该候选道路成为该GPS轨迹的可能性越大。由于正态分布的概率密度函数和余弦函数分别符合距离分数和方向分数的特性,因此距离得分和方向得分分别用以上两个函数来衡量。具体计算方法如下:
| $ {W_d} = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}}~~ \sigma }}{{\rm{e}}^{\frac{{ - {{\left( {d - \mu } \right)}^2}}}{{2{\sigma ^2}}}}};{W_a} = k \times u\cos a $ | (2) |
式中,μ= 0;以GPS平均误差范围作为标准差,即σ=r, 这里取值为5 m;a为浮动车行驶方向与道路方向夹角;k为方向因素权重系数,在路段交叉口处取得较大值。在路段交叉口处,浮动车存在3种情况:停车等待、直行通过、拐弯。3种情况下浮动车的速度较小,可通过速度值进行权重系数赋值(此处速度阈值设为2 m/s):
| $ k = \left\{ \begin{array}{l} 0.1, v < 2\\ 0.9, 其他 \end{array} \right. $ | (3) |
1) 道路连通集合间的路段转换概率。由于车辆轨迹具有时空连续性的特点,所以相邻轨迹点所在的道路应该具有一定的连通关系,这种连通关系可以使用道路扩展级别来进行度量[12]。本文采用三级连通道路,并假定当前道路与下一道路零级、一级、二级、三级连通(分别用C0、C1、C2、C3表示)的转换概率分别为1、0.9、0.8、0.4,即
| $ T\left( {e_{_{i - 1}}^{^j} \to e_{_i}^{^k}} \right) = \left\{ \begin{array}{l} 1, r \in {C_0}\\ 0.9, r \in {C_1}\\ 0.8, r \in {C_2}\\ 0.4, r \in {C_3} \end{array} \right. $ | (4) |
式中,T(ei-1j→eik)表示点pi-1第j条候选道路到pi的第k条候选道路的转换概率;r表示相邻轨迹点所在道路的连通关系。
2) 基于综合评分和候选路段转换概率的最优路径匹配法。通过筛选候选道路集以及候选道路评分计算,可以获得每个GPS点的候选道路集评分,令RSi={eij}(j=1, 2, …)为GPS点pi的候选道路集合,Wij为候选道路eij的综合评分。图 2为基于综合评分和候选道路间的转换概率获得浮动车轨迹的最优匹配路径。
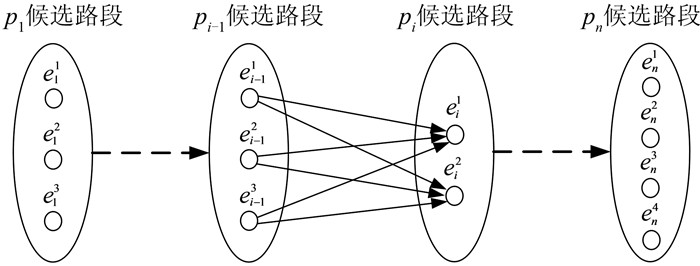 |
| 图 2 最优匹配路径 Fig.2 Optimal Matching Path |
设路径在第i(i>2)层的累积评分为S(eik),当i=1时,S(eik)=Wik,即路径的初始累积评分为路段自身的综合评分,否则当前路径的累积评分为上一点候选路径的累积评分与上一点候选路径到当前点候选路径转换概率与当前点候选路径综合评分的乘积之和。则第i层路径的累计评分计算方法为:
| $ S\left( {e_{_i}^{^k}} \right) = \max \left\{ {S\left( {e_{_{i - 1}}^{^j}} \right) + W_{_i}^{^k} \times T\left( {e_{_{i - 1}}^{^j} \to e_{_i}^{^k}} \right)} \right\}, i \ne 0 $ | (5) |
因此,到当前点所有路径中,累计评分最大的路径为最优匹配路径。
3) 最短路径拟合。在进行地图匹配时,路径的转换在某些点处容易出现中断情况(图 3),此时则以下一个GPS点作为起始点重新开始路径的匹配,对整体算法并无影响,对于两GPS点间中断的路径,用最短路径A*算法进行拟合,最终得到GPS轨迹的唯一匹配路径。
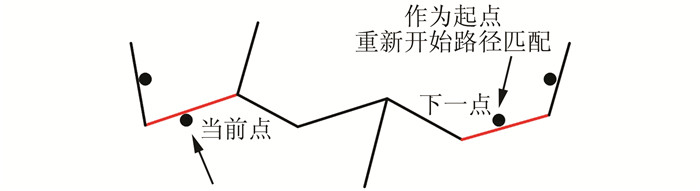 |
| 图 3 候选道路超出连通集合范围 Fig.3 Candidate Road Beyond the Scope of Connected Set |
1.4 坐标纠正
通过地图匹配算法,获得GPS轨迹点的唯一匹配路径。因此,每个GPS点对应唯一的路段,将GPS点向对应的路段投影,获得GPS点的纠正点坐标,用纠正的GPS点进行单车路段行程时间的估计。图 4展示了2013-01-01 T 00:00:00到03:00:00之间武汉市18395号浮动车轨迹地图匹配以及坐标纠正结果,其中黑色点代表纠正的GPS点。
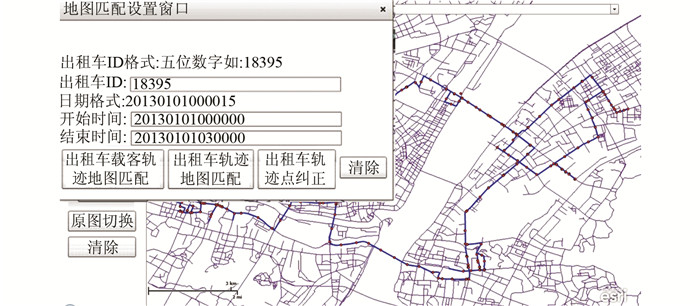 |
| 图 4 坐标纠正结果 Fig.4 Result of Coordinate Correction |
2 单车路段行程时间估计 2.1 交叉口道路中心线时刻确定方法
浮动车在路段交叉口节点附近的运行状况极为复杂。当受信号灯影响时,浮动车在交叉口停车线处等待,然后从停车启动达到一个较高的速度快速通过交叉口;当不受信号灯影响时,浮动车以较高的速度通过路段交叉口。相对于高频浮动车数据,低频浮动车在采样时间间隔内行驶的路程更远,浮动车在交叉口区域内的运行状态更为复杂。
浮动车在交叉口的通行情况[13]可以归结为路段出入口通行情况,路段出入口是相对于浮动车行驶方向而言的。浮动车通过路段入口或出口处时刻为浮动车刚刚通过或驶出路段交叉口中心线的时刻,此时不包括或应包括浮动车在入口或出口处等待交通信号灯的时间。由于浮动车沿路段直行与拐弯通过交叉口的情况类似,因此下面以直行情况为例进行分析。图 5(a)为车辆交叉口运行状态示意图,其中,虚线圆表示定位偏差圆,受GPS及GIS造成的定位偏差影响,定位偏差圆范围内的点均认为是在节点上,本文设置该距离为5 m[9];虚线框表示交叉口区域,其值为定位偏差、道路宽度以及人行横道宽度之和。设交叉口停车线到交叉口道路中心线的距离为常量δ,lmi(i=1, 2, 3, …)表示节点pm到点pi的路程,vi表示节点pi处的速度,a表示加速度,tpm表示通过节点pm的时刻。
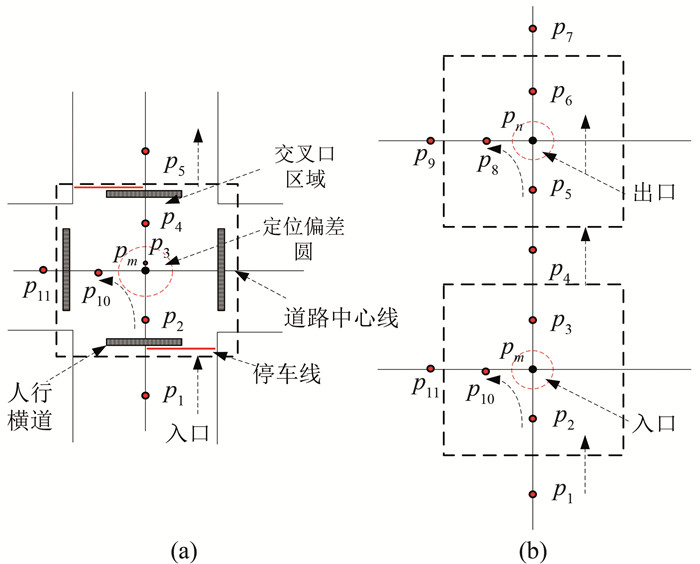 |
| 图 5 车辆交叉口区域运动特性分析 Fig.5 Movement Characteristics Analysis of Vehicle at Intersection Area |
根据现行交通法规[14],假设在交叉口区域不存在因为乘客上下车而导致停车的情况。根据坐标纠正点与路段之间的空间关系,分别估计浮动车经过路段的入口时刻和出口时刻,两时刻之差便为浮动车通过路段的行程时间。以入口为例,出口处的情况类似。图 5(b)为浮动车通过交叉口的示意图,浮动车沿着路段p1→p2→p3→…直线行驶,估计浮动车通过路段入口pm的时刻。对于低频采样点而言,浮动车采样时间间隔较长,浮动车通过交叉口区域的时刻可分为以下3种情况进行估计。
1) 目标路段上不存在GPS点,则不能估计浮动车在目标路段的行程时间。
2) 目标路段上只有一个GPS点且速度不为0,说明此时路段交通畅通,浮动车在此路段快速行驶。假设浮动车在该路段上匀速行驶,浮动车行程时间可用路段长度与速度的比值求得,即t=l/v。
3) 目标路段上有多个GPS点。
ⅰ.若p3点在定位圆内,且v3=0,则认为浮动车仍停留在交叉口停车线后停车等待,见图 5(a)。取下一个GPS点p4,若v4≠0,且在交叉口区域内,则认为浮动车从交叉口停车线到p4点匀加速行驶,则浮动车通过交叉口pm的时刻为:
| $ {t_{{p_m}}} = {t_{{p_4}}} - \Delta {t_{m4}} $ | (6) |
其中,
| $ {t_{{p_m}}} = {t_{{p_4}}} - \frac{{2{l_{m4}}}}{{\sqrt {\frac{\delta }{{\delta + {l_{m4}}}}} \times {v_4} + {v_4}}} $ | (7) |
① 若v4在交叉口区域内且为0,说明拥堵严重,认为从交叉口停车线到p4点,浮动车的运动经历了这样一个过程:在路段停车线后静止等待,然后先匀加速后匀减速至0。取下一个GPS点p5, 若v5≠0,考虑到同一目标路段拥挤程度的相似性,为简化计算,假设浮动车从交叉口中心线到p4点以v5匀减速行驶,则tpm=tp4-2lm4/v5。
② 若v4在交叉口区域外且为0,说明拥堵严重或者乘客上下车,根据浮动车载客状态剔除乘客上下车情况,则拥堵情况下计算方法同①。
③ 若v4在交叉口区域外且不为0,说明浮动车从交叉口停车线启动达到一定速度一直运行到p4,认为该路段匀速行驶,以p4点速度v4反推浮动车通过交叉口中心线的速度,则tpm=tp4-lm4/v4。
ⅱ.若p2、p3点在交叉口区域内,且v2=0,v3=0,说明整个路段拥堵严重,采用与ⅰ中①相同的处理方法,则tpm=tp3-2lm3/v4。
ⅲ.若p2、p3点在交叉口区域内,v2=0,v3≠0,说明浮动车在p2点停车等待,浮动车从路段交叉口停车线到p3点之间匀加速行驶,用p3点速度反推路段交叉口的速度, 采用与式(6)相同的处理方法,可以得到浮动车经过路段交叉口中心线的时刻为:
| $ {t_{{p_m}}} = {t_{{p_3}}} - \Delta {t_{m3}} = {t_{{p_3}}} - \frac{{2{l_{m3}}}}{{\sqrt {\frac{\delta }{{\delta + {l_{m3}}}}} \times {v_3} + {v_3}}} $ | (8) |
ⅳ.若p2、p3点在交叉口区域内,且v2≠0,v3=0,说明整个路段拥堵严重,则认为浮动车从路段交叉口中心线到p3点之间匀减速行驶,用p2点速度反推路段交叉口中心线的速度,则tpm=tp3-2lm3/v2。
ⅴ.若p2、p3点在交叉口区域内,且v2≠0,v3≠0, 则认为浮动车没有在交叉口停车线停车等待,从路段交叉口中心线到p3点之间匀速行驶,用p3点速度v3反推浮动车在路段交叉口中心线的速度,则tpm=tp3-lm3/v3。
ⅵ.若p3点在交叉口区域外,p2点任意,v3=0,则可以认为路段拥堵或者路段上有乘客上下车,根据浮动车载客状态剔除乘客上下车情况,对于道路拥堵情况,tpm计算方法同ⅱ。
ⅶ.若p3点在交叉口区域外,p2点任意,v3≠0,则认为从交叉口中心线到p3点以v3速度匀速行驶,则tpm计算方法同ⅴ。
2.2 单车路段行程时间估计基于以上分析,单车路段行程时间可根据浮动车经过出口时刻与入口时刻之差得到,即t=tn-tm,tn、tm分别为浮动车通过路段出口和入口的节点时刻。
3 实验验证为了验证本文所提出的路段行程时间估计方法的有效性,选取2014-03-10武汉市浮动车的部分GPS轨迹数据为实验数据。GPS轨迹的平均采样时间间隔为40 s,GPS点的定位精度约为15 m,实验区域选择武汉大学南门珞喻路82号路段,见图 6。
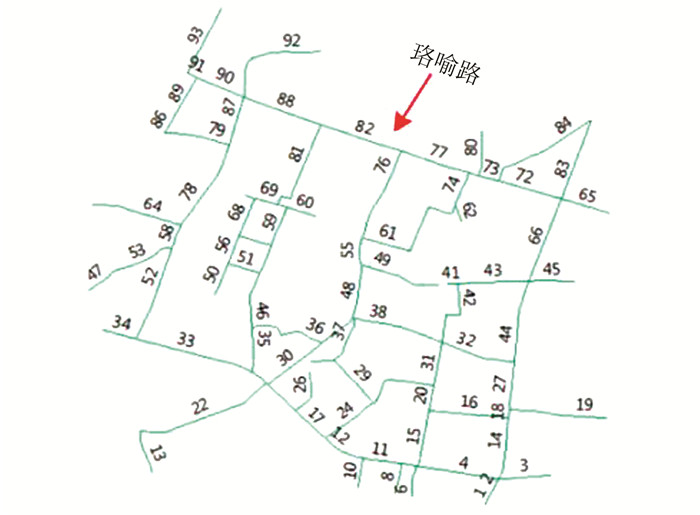 |
| 图 6 研究区域 Fig.6 Research Area |
随机选取10辆出租车轨迹,从提取的GPS轨迹中记录车辆进入路段交叉口范围并减速的时刻直到车辆进入下一个交叉口范围开始加速驶离路口的时刻,两时刻之差作为该路段通行时间的真实值。用Java语言编程实现,将采集的GPS轨迹数据进行地图匹配,然后采用本文算法进行路段行程时间估计。
利用本文方法,分别以40 s(低频)和插值得到的5 s(高频)采样时间间隔的GPS数据估计单车路段行程时间,将估计结果与真实路段行程时间进行对比。同时,利用平均速度法采用低频(40 s)浮动车数据估计路段平均行程时间,并与本文算法进行对比,实验结果如表 1所示。
| 表 1 本文方法估计结果与真实值的比较 Tab.1 Comparison of the Method of Our Proposed and Real Values |
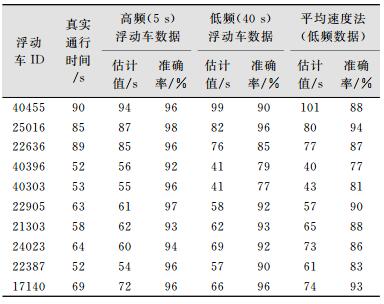 |
从表 1可以看出,相比高频浮动车数据,低频浮动车数据估计单车路段行程时间除几个异常值估计准确率较低外,大部分估计精度在90%左右。这说明在没有高频浮动车数据时,利用低频浮动车轨迹数据也能够实现路段通行时间的准确探测,且结果符合实际交通情况。表 1结果表明,就低频浮动车数据而言,本文所提出的考虑交叉口运行状态的方法要比平均速度法估计结果的准确率高。
4 结束语本文以浮动车轨迹数据为研究对象,利用低频轨迹数据估计单车路段行程时间,更真实地反映了路段中车流运行状态。实验结果表明,在缺失高频浮动车数据时,采用本文算法,利用低频浮动车轨迹数据也能够实现单车路段行程时间的准确探测。
| [1] |
张和生, 张毅, 胡东成. 路段平均行程时间估计方法[J]. 交通运输工程学报, 2008, 8(1): 89-96. |
| [2] |
Wu C H, Ho J M, Lee D T. Travel Time Prediction with Support Vector Regression[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 276-281. DOI:10.1109/TITS.2004.837813 |
| [3] |
Sun Lu, Yang Jun, Mahmassani H. Travel Time Estimation Based on Piecewise Truncated Quadratic Speed Trajectory[J]. Transportation Research (Part A), 2008, 42(1): 173-186. |
| [4] |
Zheng F, Zuylen H V. Urban Link Travel Time Estimation Based on Sparse Probe Vehicle Data[J]. Transportation Research (Part C): Emerging Technologies, 2013, 31(31): 145-157. |
| [5] |
Jenelius E, Koutsopoulos H N. Travel Time Estimation for Urban Road Networks Using Low Frequency Probe Vehicle Data[J]. Transportation Research (Part B): Methodological, 2013, 53(4): 64-81. |
| [6] |
张和生, 张毅, 温慧敏, 等. 利用GPS数据估计路段的平均行程时间[J]. 吉林大学学报(工学版), 2007, 37(3): 533-537. |
| [7] |
张玮. 基于GPS浮动车的路径行程时间估计系统关键技术研究[D]. 长春: 吉林大学, 2011 http://cdmd.cnki.com.cn/Article/CDMD-10183-1013299526.htm
|
| [8] |
韦安. 两种基于浮动车数据的实时路况预测模型比较[J]. 测绘地理信息, 2015, 40(4): 73-75. |
| [9] |
董红召, 吴方国. 基于FCM的路段平均行程时间估计[J]. 科技通报, 2011, 27(3): 426-430. |
| [10] |
于德新, 高学英, 杨兆升. 基于GPS数据及车辆运行特性分析的单车路段行程时间估计[J]. 吉林大学学报(工学版), 2010, 40(4): 965-970. |
| [11] |
杨兆升. 城市交通流诱导系统[M]. 北京: 中国铁道出版社, 2004.
|
| [12] |
张涛, 杨殿阁, 李克强, 等. 车辆导航中带匹配度反馈的模糊地图匹配算法[J]. 清华大学学报(自然科学版), 2009, 49(2): 277-280. |
| [13] |
李清泉, 胡波, 乐阳. 一种基于约束的最短路径低频浮动车数据地图匹配算法[J]. 武汉大学学报·信息科学版, 2013, 38(7): 805-808. |
| [14] |
中华人民共和国住房和城乡建设部. 城市道路交叉口规划规范: GB 50647-2011[S]. 北京: 中国计划出版社, 2011
|
 2018, Vol. 43
2018, Vol. 43

