| 基于局部拟合平面投影搜索最近点的ICP配准 |
目前,用于测绘领域的三维激光扫描仪的扫描距离长度一般超过50 m,有些甚至达到1 500 m,该功能的发展使得三维激光扫描技术由先前用于扫描小目标物体逐渐发展到扫描宏观的目标物体对象,如城市中的高层建筑物[1]、水利工程中的大型水工建筑物[2]及交通工程中的道路桥梁[3]等。
众所周知,大型人工建筑物的三维体一般是由基本的几何形体构成,轮廓一般由点、线、面等基本几何要素构成,建筑物表面一般由简单的几何形体构成,很少由自由形态的曲面构成,而传统迭代最近点(iterative closest point, ICP)配准方法是基于自由形态曲面的配准方法,效率较低且收敛速度较慢[4]。因此,本文利用建筑物的几何特征,结合扫描数据的特点,采用局部平面搜索最近点的方法对建筑物表面的三维激光扫描数据配准方法进行改进。
1 改进的ICP配准算法原理改进的ICP配准算法与原始ICP配准算法[5]步骤原理相同,其不同之处在于最近点的选择过程,本文采用对最近点的邻域点进行局部平面拟合的方法,确定对应点的点对位置。
拟合是一种非常实用的数据处理方法,这种方法能很大限度地反映离散点之间的近似函数关系,且能降低数据量并过滤掉部分噪点。对于点集中的一点p0,找出与其距离小于邻域值dλ的点,设为点pi(i=1, 2, …, n),并对此n个邻域点进行平面拟合,进而得到平面法线和拟合误差。邻域点拟合的三维平面可用海塞公式表示,确定其法向量和平面方程[6]后, 可以进一步求出参考点集中任意一点p(xp, yp, zp)在平面ux+uy+uz-d=0的投影点t(xt, yt, zt)[7],比较参考点集中的点p(xp, yp, zp)与计算的投影点t(xt, yt, zt)之间的距离,取距离最小时的点ti作为点pi的对应点。
2 改进的ICP配准算法关键问题1) 粗配准。三维激光扫描数据的粗配准是在坐标变换基础上进行的,坐标由三维几何变换而来,其基本原理是通过特征点计算变换矩阵,从而实现整体的坐标变换。通常使用4个公共特征点进行粗配准,利用4个特征点坐标可求得点云2至点云1的变换参数,将此变换参数运用于整个点集的变换,即可完成点云的粗配准。一般认为点云配准时其坐标变换为刚性变换,只包含点云的平移与旋转,不包含投影和缩放,所以只需解算旋转和平移6个坐标变换参数。
2) 配准区域的选择。在实际应用中,利用人机交互一般只能进行粗配准,不能完成很细致的工作,直接影响配准结果及其效率。在配准区域选择的过程中,距离阈值的选取依赖于专业人员的素质及熟练程度,由于粗配准效果不是很好,阈值应大于两幅点云的扫描间隔,才能保证将正确的待配准点选入到配准区域中。
3) 局部平面搜索最近点步骤。①对于参考点集中的任意一点p,根据目标点集中的点q确定其距离小于给定阈值的邻域点;②根据q点的邻域点,确定拟合的最小二乘平面方程;③依次遍历点集Q,根据点集Q中的点对其进行平面拟合,向各平面方程作垂线,得垂足点,判断点p与垂足点间的距离,计算并记录点p与各个垂足点之间的距离,记录距离最小值时的垂足点;④距离最小时取其垂足点,即为p点的对应点。
4) 矩阵特征向量解算。本文采用幂法求解矩阵最大特征向量,它是一种按模最大特征值求任意矩阵对应特征向量的迭代算法[8],该方法最大的优点是计算简单,容易在计算机上实现,但有时收敛速度较慢。
假设4×4的正定矩阵N有4个线性无关的特征向量X1、X2、X3、X4,而相应的特征值满足|λ1| > |λ2| > |λ3| > |λ4|,取初始向量V0= U0=(1, 1, 1, 1)T,利用幂法求解最大特征向量步骤:①任意给定n维初始向量V0= U0=(1, 1, 1, 1)T;②并根据Vk+1= NU (k=0, 1, 2, …)计算矩阵Vk+1;③根据矩阵Vk+1中的元素,计算矩阵Vk+1的各个按模分量,假设为(C1, C2, C3, C4), 并寻找(C1, C2, C3, C4)中的最大值,设为Ci;④计算Uk= Vk/(Vk)max;⑤判断Ci的两次之差的绝对值,若大于给定数值,则重复步骤②~步骤④;若小于给定数值,则跳出循环,与(Vk)max对应的向量Uk就是最大特征向量。
由上述步骤可知,幂法求解矩阵最大特征向量是迭代计算的过程,其精度较高,但是受迭代过程的影响,计算速度较慢。对于矩阵最小特征向量解算问题,需求出该矩阵的逆矩阵,再利用幂法计算逆矩阵的最大特征值及特征向量,为原矩阵最小的特征值和特征向量。
5) 三维数据配准精度度量。由于测量数据中伴随误差,因此,必须研究配准参数对误差的敏感性,通常测量误差、扫描数据的点数和扫描点的位置都会影响配准结果。由于很难确定三维激光扫描数据配准参数真值。因此,只能通过对应点点对间的距离来衡量配准精度,衡量的指标有归一化残差和、归一化残差平方和、最大残差及残差均方差4种。4个精度指标中,归一化残差和与所要求的配准精度的度量不同,最大残差对误差非常敏感,因此,这两项不适合作为配准精度的指标。对配准后的点集而言,残差均方差值一般小于归一化残差平方和值,本文采用残差均方根误差(root mean square error,RMSE)作为配准精度的度量指标[9]。
3 实例应用及分析采用Trimble GX[10]对某高层建筑物进行扫描,ICP配准算法对数据的要求较高,并非所有的有一定重叠度的点云之间都可以利用ICP配准算法进行配准参数的计算,且用于点云配准的两幅点云必须在三维空间中正交的3个方向上均有足够的重叠分量才能稳定可靠地解算出配准参数。因此,为了提高点云配准效果及其配准效率,笔者在实验中所用的建筑物三维激光扫描数据是从不同的角度对建筑物进行的扫描,并且数据在3个正交方向上均有一定的重叠度,能满足配准的基本要求。
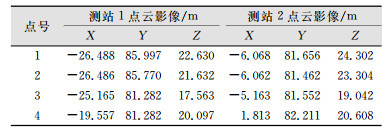
3.1 粗配准粗配准的目的是为ICP配准算法迭代计算配准参数提供近似值初始值,因此,粗配准的精度可以影响配准计算的收敛次数。由于在数据采集过程中未设置任何标签或标靶等特征点,因此,本文利用人机交互的方法选取要求不高的公共点,考虑到站点扫描角度的不同,笔者在人工选取特征点时选取两站点都能扫描到的明显特征,且使同名点对均匀分布,从而保证了配准达到最优。两幅点云影像中提取的4组公共特征点对坐标如图 1和表 1所示。
 |
| 图 1 两点云数据中4组公共特征点对 Fig.1 Four Sets of Common Feature Point Pairs in Two-Point Cloud Data |
| 表 1 点云影像中点云数据提取的4组公共特征点对坐标 Tab.1 Sets of Common Feature Point Pairs Extracted from Point Cloud Data in Point Cloud Images |
 |
通过这4组特征点对求得的两测站数据配准的中误差为0.837 m,根据这些点对求解数据配准模型,解算得到的旋转矩阵R0和T0分别为:
| $ \begin{array}{l} {\mathit{\boldsymbol{R}}_0} = \left[ {\begin{array}{*{20}{c}} {0.764\;78}&{0.701\;7}&{ - 0.133\;8}\\ { - 0.635\;70}&{0.880\;3}&{0.052\;5}\\ {0.134\;40}&{0.082\;3}&{0.984\;8} \end{array}} \right]{\rm{;}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{T}}_0} = \left[ {\begin{array}{*{20}{c}} { - 75.894\;0}\\ {8.978\;4}\\ { - 7.210\;2} \end{array}} \right] \end{array} $ |
粗配准后误差较大,采用的配准数据简化后的点云1的平均间隔为46 mm,点云2的平均间隔为60 mm,为了保证将待配准区域中的点都选入配准计算,本文设定阈值为0.6 m。
本文利用特征点坐标进行粗配准,在此基础上让计算机自动识别配准区域,具体方法如下:在经粗配准后的参考点集B′中,寻找与目标点集A中的点ai距离最近的点,并计算最近距离值,判断此距离值与给定距离阈值0.6的关系:若大于0.6,则认为不在配准区域范围之内,并删除点ai;若小于0.6,则认为在配准区域范围之内,记录点ai和其最近点qi,并分别放入点集P和S。将目标点集A中的所有点进行上述计算和判断,得到最终点集P和S即为目标点集和参考点集的公共配准区域。
3.3 改进的ICP配准算法结果分析经过粗配准后,利用原始ICP配准算法和改进的ICP配准算法对建筑物三维激光数据进行配准,得到了良好的配准效果。由于粗配准人工选取特征点的误差较大,在传统ICP配准过程中出现了部分未吻合的现象,如图 2(a)所示;在粗配准基础上改进的ICP配准中两幅点云数据的吻合情况比较好,如图 2(b)所示。
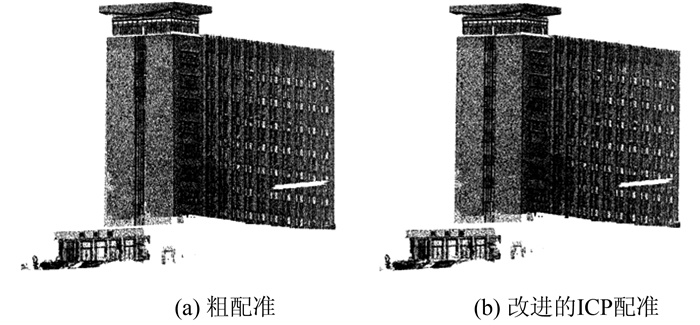 |
| 图 2 粗配准和改进的ICP配准结果 Fig.2 Rough and Improve ICP Registration Results |
传统ICP配准结果局部放大如图 3(a)所示,明显可以看到底部发生错位现象,主要是因为配准采用的特征点云数据位于建筑物顶部,距离建筑物底部较远所致。改进的ICP配准结果如图 3(b)所示,可以看到底部未发生错位现象,进而证明改进的ICP配准算法吻合效果良好。
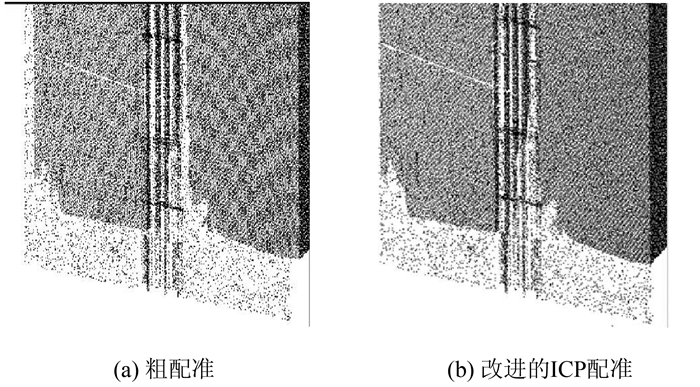 |
| 图 3 粗配准和改进的ICP配准局部放大 Fig.3 Rough and Improve ICP Registration Results by Partial Amplification |
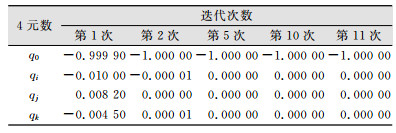
在不同迭代次数情况下,改进ICP配准算法4元数及其矩阵参数的计算结果分别如表 2和表 3所示,原始ICP配准算法与改进的ICP配准算法,配准后精度指标计算结果如图 4所示。
| 表 2 改进ICP配准算法4元数计算参数 Tab.2 Improved ICP Registration Algorithm Quaternion Calculation Parameters |
 |
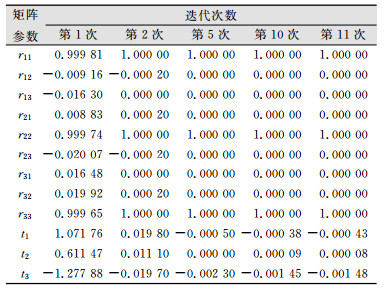
| 表 3 改进ICP配准算法矩阵计算参数 Tab.3 Improved ICP Registration Algorithm Matrix Calculation Parameters |
 |
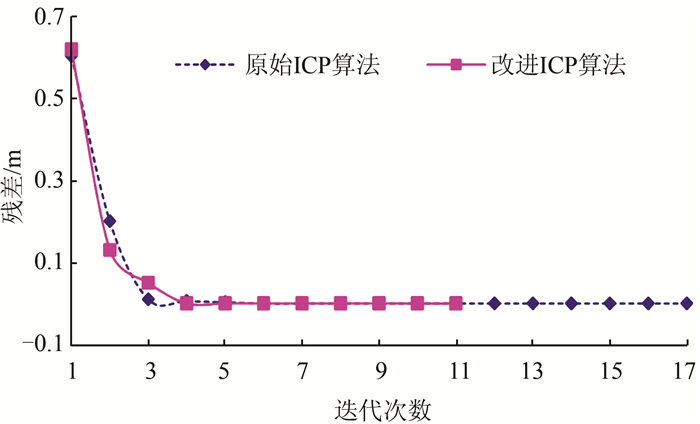 |
| 图 4 配准迭代误差 Fig.4 Registration Iteration Error |
由表 2和表 3可知,改进的ICP配准算法迭代至后续变换参数较小时,其旋转矩阵为单位矩阵,即不发生旋转,只有微小的平移量,这是由配准数据决定的,不同的数据求解的旋转参数和平移矩阵不同,但当迭代收敛较稳定时,旋转矩阵趋于单位矩阵,平移矩阵的值较小。
一定程度上,采用的配准初始值较好地保证了算法的可行性,从图 4可知,原始ICP配准算法和改进ICP配准算法残差均在逐步减小。
分析图 4可知,原始ICP配准算法迭代17次,残差收敛至0.002 232 213 m,改进ICP配准算法迭代11次,残差收敛至0.002 184 674 m,可见由于采用的配准数据相同,改进ICP配准算法与原始ICP配准算法收敛的残差精度保持一致,收敛次数充分证明,运用改进后的ICP配准算法在迭代的效率上优于原始ICP配准算法。
4 结束语三维激光扫描数据配准要保证其正确性与准确性,本文针对海量三维激光扫描数据的配准,提出了基于局部拟合平面投影搜索最近点的改进ICP配准算法,重点研究了算法实现过程中最近点搜索、迭代收敛性以及配准自由度等问题,并进一步分析了改进ICP配准算法的处理速度和配准精度。最后以Microsoft Visual Studio 2012为平台,运用C#语言将改进的ICP配准算法和原始ICP配准算法程序化,通过实测数据及自编程序进行了实验,结果表明,对于三维激光扫描数据,改进的ICP配准算法较原始ICP配准算法具有更好的收敛性和配准效率。
| [1] |
林卉, 王李娟, 康志忠, 等. 三维激光扫描建筑物立面数据的自动提取[J]. 测绘通报, 2016(10): 25-30. |
| [2] |
吴蒙.基于三维激光扫描技术的建筑物建模研究[D].抚州: 东华理工大学, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10405-1015990442.htm
|
| [3] |
邓晓隆, 田石柱. 基于三维激光扫描的桥梁变形检测及数据处理[J]. 激光与光电子学进展, 2018, 55(7): 286-291. |
| [4] |
陈春旭, 漆钰晖, 朱一帆, 等. ICP配准算法的影响因素及评价指标分析[J]. 导航定位与授时, 2018, 5(5): 67-72. |
| [5] |
张步.三维激光点云数据配准研究[D].西安: 西安科技大学, 2015 http://cdmd.cnki.com.cn/Article/CDMD-10704-1016901950.htm
|
| [6] |
陈汉清, 王乐洋. 点云数据平面拟合的加权总体最小二乘方法[J]. 工程勘察, 2015, 43(11): 59-63. |
| [7] |
黄延祝, 成孝予. 线性代数与空间解析几何[M]. 2版. 北京: 高等教育出版社, 2003.
|
| [8] |
曾莉, 肖明. 计算实对称矩阵特征值特征向量的幂法[J]. 南昌大学学报(理科版), 2016, 40(4): 399-402. DOI:10.3969/j.issn.1006-0464.2016.04.017 |
| [9] |
周才文.基于地面三维激光扫描的露天矿山边坡变形监测研究[D].赣州: 江西理工大学, 2018 http://cdmd.cnki.com.cn/Article/CDMD-10407-1018215946.htm
|
| [10] |
齐建伟, 朱恩利. Trimble GX 3D激光扫描仪内符合精度的试验[J]. 测绘科学, 2013, 38(4): 63-64. |
 2019, Vol. 44
2019, Vol. 44

