| 惠州市似大地水准面精度检测研究 |
根据国家测绘地理信息局《关于印发启用2000国家坐标系实施方案的通知》,广东省国土资源厅结合该省测绘工作的实际情况,于2009年编制了《广东省2000国家大地坐标系转换工作实施细则》,按细则要求,惠州市于2013-2014年间立项并完成了全市现代测绘基准及服务体系建设项目。通过此项目,不仅建立了与全省统一的2000国家坐标系,还完成了惠州市高精度似大地水准面模型建设工作。
1 惠州市似大地水准面惠州市似大地水准面计算中,使用了6 378个点重力数据和167个GNSS水准资料,GGM03C地球重力场模型作为参考重力场,由第二类Helmert凝集法完成了大地水准面的计算。根据项目设计要求,在项目建设过程中,在惠州市内较均匀地选取了同精度观测的40个B/C级网点作为检核点。检测点位分布见图 1,图中B006和B001点为B级网点,其余点为C级网点。
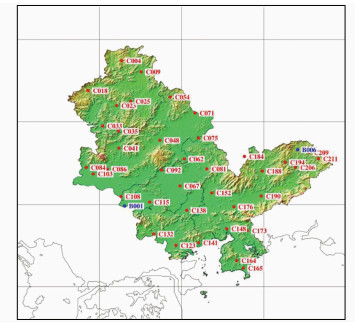 |
| 图 1 检测点位分布图 Figure 1 Distribution of Check Points |
利用所确定的CGCS2000的大地纬度、经度和大地高,根据已有的似大地水准面模型和软件[1-10],可计算出相应的正常高。然后比较计算的正常高和水准测得的正常高,确定出其差值,并求出标准差。检测点计算的正常高和水准测得的正常高差值及统计表如表 1所示。由表 1可知,似大地水准面的精度为0.01 m。
| 表 1 检测点计算的正常高和水准测得的正常高差值统计表 Table 1 Difference Between Normal Heights Calculated by Check Points and Leveling |
 |
为进一步检验惠州市似大地水准面模型在应用中的精度,从同等级静态检测、低等级静态检测及CORS动态检测三方面进行了进一步的检测。
2 检测方法 2.1 同等级静态测量方式检测同精度静态测量方式检测是按规范抽样标准,在惠州市范围内均匀选取了22个B/C级网点作为检核点,利用同精度所测定的CGCS2000的大地纬度、经度、大地高和二等水准成果,再根据提供的似大地水准面模型和软件计算出相应的正常高。比较计算的正常高和二等水准测得的正常高,确定出其差值,并求出检测中误差。
检测点布设主要选择在平坦地区、丘陵地区、山地和边缘地区4个区域,要求均匀分布,平原区域、丘陵地区和山地均布设6个点,有效边缘区域布设4个点,检测点总数为22个。
检测点与用于区域似大地水准面精化高程异常控制点间的距离应不小于似大地水准面格网间距,因此本项目检测点与高程异常控制点间的距离均大于2 km。检验点应同时满足GPS观测与水准联测条件,布点情况见图 2。
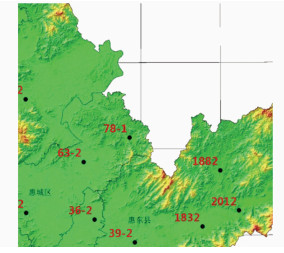 |
| 图 2 同等级精度检测点分布图 Figure 2 Distribution of Check Points at the Same Grade Precision |
检验点GPS测量按GPS-C级网的精度要求实施,同步图形之间采用边连式,作业模式为静态定位,采用6台GPS接收机同步观测,全网共观测5个同步环,每个同步环观测1个时段,每个时段连续观测4 h以上,其他各项指标按照GB/T 18314-2009中10.1.2表 5有关GPS-C级的规定。
水准联测按国家二等水准测量精度要求实施,采用自动安平电子水准仪及条码式因瓦标尺观测,以附近新布设的一、二等水准点为起算点,按单程支线方式联测。其他要求按GB/T 12897-2006相关规定执行。
GPS测量数据处理按GB/T 18314-2009要求实施,获得准确的大地坐标、大地高。利用检验点的大地坐标和似大地水准面模型计算各检验点的高程异常。
二等水准测量数据处理按GB/T 12897-2006要求实施,获得几何水准高。由检验点的大地高减去水准高计算出各检验点的实测高程异常。
由似大地水准面模型计算的各检验点高程异常值与其实测高程异常值进行比较,统计出不符值中误差,以检验似大地水准面计算模型的正确性,并对结果进行精度评定。
2.2 低等级静态测量方式检测惠州市现代测绘基准及服务体系建设项目中包括了惠城区范围(含仲恺高新区)常规控制网建立部分,完成了惠城区300个E级GPS点和100个三等水准点的建设。在所有新建控制点中,有55个E级GPS点具有三等水准高程成果。55个E级点均匀分布于惠城区范围,利用其所测定的CGCS2000的大地纬度、经度、大地高,结合似大地水准面模型,可以计算出相应的正常高。然后比较计算的正常高和三等水准精度测得的正常高,确定出其差值,并求出检测中误差,评定似大地水准面模型在局部范围内的应用精度。点位分布情况见图 3。
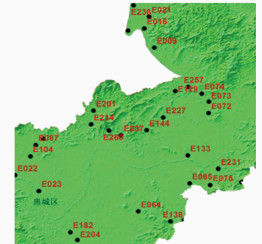 |
| 图 3 低等级精度检测点分布图 Figure 3 Distribution of Check Points at the Low Grade Precision |
E级GPS点施测以B/C级GPS点为起算,共联测了6个起算点。外业观测采用8台中海达V8型双频(5+1×10-6)接收机进行数据采集,观测量为载波相位。采用GPS静态定位模式观测,构成的最小闭合环或附合路线中的边数小于6条。观测时段长度大于45 min,观测时段数大于1.6。其余要求按规范执行。
三等水准测量采用新布设的一、二等水准点为起算点,共连测7个高等级水准点。水准测量观测采用高精度数字水准仪进行,采用中丝法读数进行往返测,电子记录观测数据。
E级GPS网基线采用中海达HGO数据处理软件包进行,使用武汉大学GNSS中心的PowerNet软件进行各项平差,平差分别在CGCS2000坐标系、HZCORS采用的框架(ITRF2000框架,2006.9历元)下进行。
三等水准概略高差计算中加入了水准标尺尺长改正和正常水准面不平行改正,概算高程闭合差合格后,应用EpsNas2008智能图文网平差系统,以测段距离定权,按经典网进行水准网严密平差。平差获得与二等水准网一致的1985国家高程成果,全网的高程中误差为2 mm,最弱点高程中误差为9.5 mm。
由E级点结合似大地水准面模型计算的各检验点正常高与其实测三等水准高程进行比较,统计出不符值中误差,以检验似大地水准面计算模型的正确性,并对结果进行精度评定。
2.3 CORS系统动态检测惠州市高精度似大地水准面模型与HZCORS相结合,能很好地提高CORS应用中正常高的精度,改变传统作业方式,提高作业效率。因此在CORS中的应用精度是似大地水准面模型应用的关键。本项目在惠州市范围内均匀选取了新布设的21个B/C级网点作为检核点,利用HZCORS实时观测点位大地高,并利用似大地水准面模型拟合得到正常高,用拟合得到的正常高与点位二等水准正常高进行比较,检核CORS的应用精度,并求出检测中误差。选点要求尽量均匀分布各类地形,点位分布见图 4。
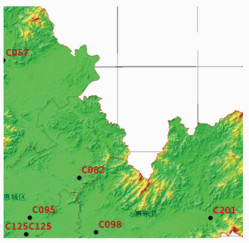 |
| 图 4 动态测量检测点分布图 Figure 4 Distribution of Dynamic Measurement Check Points |
检测点测量按网络RTK图根要求测量,在每个观测点使用三脚架或对中杆架设仪器,且量取仪器高两次,开机前后各一次。每点需初始化两次,两次初始化成果在野外进行实时比对,要求比对值较差小于5 cm。如果3次较差均超出精度指标,则在其他时间段重新观测。每个检测点每次初始化观测历元不少于60个。观测结果取两次观测所有历元成果的平均值,利用HZCORS结合似大地水准面模型实时解算得到正常高。将测得的正常高与检测点二等水准成果进行比对,求出较差中误差。
3 检测精度 3.1 同等级静态测量检测同等级静态测量检测点正常高较差见表 2。
| 表 2 同等级静态测量检测点正常高较差表 Table 2 Normal Height Difference of the Same Grade Precision Check Points |
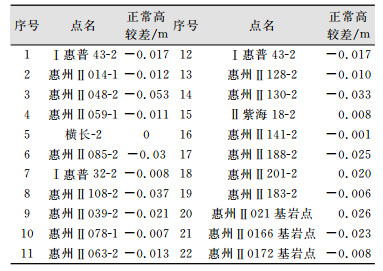 |
按中误差公式
低等级静态测量检测点正常高较差见表 3。
| 表 3 低等级静态测量检测点正常高较差表 Table 3 Normal Height Difference of the Low Grade Precision Check Points |
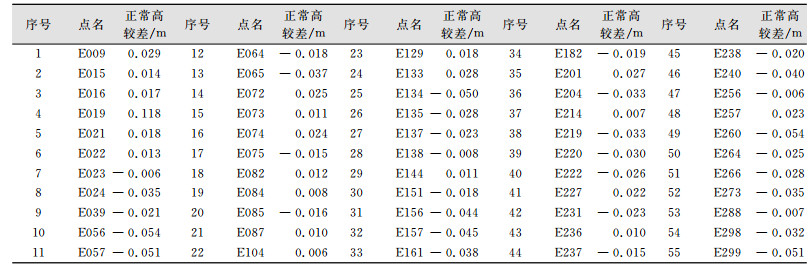 |
剔除粗差E019后,按
CORS系统动态检测点正常高较差见表 4。
| 表 4 动态检测点正常高较差表 Table 4 Normal Height Difference of Dynamic Measurement Check Points |
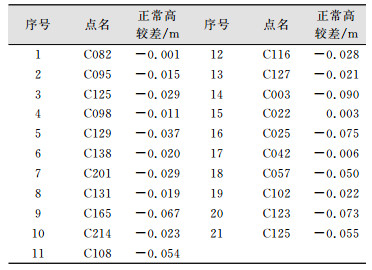 |
按中误差公式
通过多种方式的外业检测可知,惠州市似大地水准面模型在常规静态应用层面精度优于2 cm,在与HZCORS相结合的实时动态应用层面精度优于5 cm,可以直接应用于工程测量。
根据误差传递理论,拟合高程误差与似大地水准面模型误差和大地高误差相关,其关系为m拟=
| [1] | 张正禄, 邓勇, 罗长林, 等. 利用GPS精化区域似大地水准面[J]. 大地测量与地球动力学, 2006, 26(4): 14–17 |
| [2] | 廖超明, 王龙波, 覃允森. 一种有效的区域似大地水准面精度检测方法[J]. 测绘科学, 2008, 33(6): 53–54 |
| [3] | 畅毅, 姜卫平. 局部似大地水准面精化技术及其应用现状分析[J]. 物探装备, 2006, 16(4): 255–260 |
| [4] | 刘成宝, 牛守明, 刘曦灿. 济南市似大地水准面外部检核研究[J]. 城市勘测, 2009, (6): 52–54 |
| [5] | 徐亚明, 王佩军, 邱青松. GPS水准测量及对试验网的处理[J]. 东北测量, 2001, (1): 13–14 |
| [6] | 孙建华, 马飞虎, 饶琴. 杭州市滨江区似大地水准面的确定及精度分析[J]. 测绘信息与工程, 2004, 29(1): 11–12 |
| [7] | 宁津生, 罗志才, 李建成. 我国省市级大地水准面精化的现状及技术模式[J]. 大地测量与地球动力学, 2004, 24(1): 4–8 |
| [8] | 宋玉兵, 朱风云. 江苏省域似大地水准面成果的应用分析[J]. 测绘通报, 2003, (12): 6–8 DOI: 10.3969/j.issn.0494-0911.2003.12.003 |
| [9] | Zhang K. On the Determination of a New Australian Geoid[J]. Phys Chem Earth(A), 1999, 24(1): 61–66 DOI: 10.1016/S1464-1895(98)00011-8 |
| [10] | 施一民, 施宝湘. 提高GPS水准解算精度的一种新方法[J]. 同济大学学报自然科学版, 2000, 28(4): 426–429 |
 2017, Vol. 42
2017, Vol. 42

