| 全站仪任意坐标系三维变形监测方法 |
在工程测量工作中,使用全站仪的变形监测方法很多[1-3]。根据变形监测工作的需要,对于工程变形的全站仪三维变形监测,其方法之一是在变形体范围内布置若干个变形监测点,而在变形体之外至少应该建立3个以上已知控制点,一个控制点用于架设全站仪,另外两个控制点作为后视点和检查点,利用控制点的三维坐标推算出变形监测点的三维坐标,将后次观测得到的监测点的三维坐标与初始观测得到的监测点的三维坐标即初始值进行比较,以发现监测点的变化情况。对于上述这种三维变形监测方法,用于监测的设站点、后视点和检查点以及监测点的初始值三维坐标首先要通过控制测量工序确定为已知。对于高精度精密变形监测工作,还需要先建立固定观测墩,作为设站点的控制点就建立在观测墩上。若监测精度要求不高,则可以不建立观测墩,这种情况下,控制点建立在地面上,每次监测都需要精确量取仪器高。若监测精度要求高而又不建立观测墩,为了提高全站仪的仪器量高精度,则可以采用虚拟观测墩技术[4]。对于这种变形监测工作,全站仪需要严格对中,若平面监测精度要求越高,则对中要求就越严格。监测所用的坐标系可以采用国家统一坐标系,也可以建立独立直角坐标系,在监测工作开始前,坐标系要唯一确定下来,并且在监测期间坐标系一般不能改变。为此,本文提出一种全站仪任意坐标系三维变形监测方法,对目前这种工程变形监测方法[5-7]进行改进,克服上述一些不足,通过改进,使得这种变形监测工作简便灵活、省时省力、方便快捷、工序少、节约资源、降低工程造价。
1 全站仪三维变形监测方法 1.1 单站观测 1.1.1 位移计算公式初始观测时,在任何位置设站观测各点,设
| $ \begin{gathered} \;\;\;\;\;\;{\left( {\Delta x_j^0\;\Delta y_j^0\;\Delta z_j^0} \right)^{\text{T}}} = {\left( {x_j^0\;y_j^0\;z_j^0} \right)^{\text{T}}} - \hfill \\ {\left( {x_A^0\;y_A^0\;z_A^0} \right)^{\text{T}}}\left( {j \ne A,j = 1,2,3, \ldots ,n,B} \right) \hfill \\ \end{gathered} $ | (1) |
初始观测后得到AB的初始方位角为:
| $\alpha _{AB}^{0}={{\tan }^{-1}}\left( \Delta y_{B}^{0}/\Delta x_{B}^{0} \right)$ | (2) |
而
后次观测时,同样在任何位置设站观测各点,设
| $ \begin{gathered} {\left( {\Delta x_j^i\;\Delta y_j^i\;\Delta z_j^i} \right)^{\text{T}}} = {\left( {x_j^i\;y_j^i\;z_j^i} \right)^{\text{T}}} - {\left( {x_A^i\;y_A^i\;z_A^i} \right)^{\text{T}}} \hfill \\ \left( {j \ne A,j = 1,2,3, \cdots ,n,B} \right) \hfill \\ \end{gathered} $ | (3) |
后次观测得到AB的方位角为:
| $\alpha _{AB}^{i}={{\tan }^{-1}}\left( \Delta y_{B}^{i}/\Delta x_{B}^{i} \right)$ | (4) |
而
由于所有点的后次观测与初始观测都已经过平移变换为以A点为坐标原点,所以需要将后次观测的结果旋转变换到初始观测坐标系中。设旋转角为Δαi,则:
| $\Delta {{\alpha }_{i}}=\alpha _{AB}^{i}-\alpha _{AB}^{0}$ | (5) |
式中,Δαi为AB方向后次第i次观测方位角与初始观测方位角之差。
将后次第i次观测得到的监测点在以A点为坐标原点的后次观测坐标系坐标旋转变换到以A点为坐标原点的初始观测坐标系中的坐标为:
| $\left( \begin{matrix} \Delta x_{j}^{{{i}''}} \\ \Delta y_{j}^{{{i}''}} \\ \end{matrix} \right)=k\left( \begin{matrix} \cos \Delta {{\alpha }_{i}}\ \ -\sin \Delta {{\alpha }_{i}} \\ \sin \Delta {{\alpha }_{i}}\ \ \cos \Delta {{\alpha }_{i}} \\ \end{matrix} \right)\left( \begin{matrix} \Delta x_{j}^{i} \\ \Delta y_{j}^{i} \\ \end{matrix} \right)$ | (6) |
式中,k=1。
用前缀⊿表示位移,设监测点的位移为
| $\begin{align} &{{\left( ⊿ x_{j}^{i}\ ⊿ \Delta y_{j}^{i}\ ⊿ \Delta z_{j}^{i} \right)}^{\text{T}}}={{\left( \Delta x_{j}^{{{i}''}}\ \Delta y_{j}^{{{i}''}}\ \Delta z_{j}^{{{i}''}} \right)}^{\text{T}}}- \\ &{{\left( \Delta x_{j}^{0}\ \Delta y_{j}^{0}\ \Delta z_{j}^{0} \right)}^{\text{T}}}\quad \left( j=1, 2, 3, \cdots, n \right) \\ \end{align}$ | (7) |
综合式 (1)、(3)、(6)、(7) 得位移计算公式为:
| $ \left( \begin{matrix} ⊿ \Delta x_{j}^{i} \\ \begin{matrix} ⊿ \Delta y_{j}^{i} \\ ⊿ \Delta z_{j}^{i} \\ \end{matrix} \\ \end{matrix} \right)=\left( \begin{matrix} \cos \Delta {{\alpha }_{i}} &-\sin \Delta {{\alpha }_{i}}&0 \\ \sin \Delta {{\alpha }_{i}}&\cos \Delta {{\alpha }_{i}}&0 \\ 0&0&1 \\ \end{matrix} \right)\left( \begin{matrix} \begin{matrix} x_{j}^{i}-x_{A}^{i} \\ y_{j}^{i}-y_{A}^{i} \\ \end{matrix} \\ z_{j}^{i}-z_{A}^{i} \\ \end{matrix} \right)-\left( \begin{matrix} \begin{matrix} x_{j}^{0}-x_{A}^{0} \\ \begin{matrix} y_{j}^{0}-y_{A}^{0} \\ \end{matrix} \\ \end{matrix} \\ z_{j}^{0}-z_{A}^{0} \\ \end{matrix} \right) $ | (8) |
设第j点在后次第i次监测得到的平面点位位移为dji,则
| $d_{j}^{i}=\sqrt{⊿ \Delta x{{_{j}^{i}}^{2}}+⊿ \Delta y{{_{j}^{i}}^{2}}}$ | (9) |
位移方位角为:
| $ \alpha _{j}^{i}={{\tan }^{-1}}(⊿ \Delta y_{j}^{i}/⊿ \Delta x_{j}^{i}) $ | (10) |
式中,αji为第j点在第i次监测时在初始观测坐标系中的位移方位角。位移方位角表示位移的方向。
根据实际工作情况,当采用统一坐标系,此时⊿αi=0,代入式 (8) 后得:
| $\left[\begin{gathered} ⊿ \Delta x_j^i \hfill \\ ⊿ \Delta y_j^i \hfill \\ ⊿ \Delta z_j^i \hfill \\ \end{gathered} \right] = \left[\begin{gathered} x_j^i-x_A^i \hfill \\ y_j^i-y_A^i \hfill \\ z_j^i-z_A^i \hfill \\ \end{gathered} \right] - \left[\begin{gathered} x_j^0-x_A^0 \hfill \\ y_j^0-y_A^0 \hfill \\ z_j^0-z_A^0 \hfill \\ \end{gathered} \right]$ | (11) |
对式 (8) 求全微分并转换为中误差形式,得:
| $ \left\{ \begin{align} &m_{⊿ \Delta x_{j}^{i}}^{2}={{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial \Delta {{\alpha }_{i}}} \right)}^{2}}m_{\Delta {{\alpha }_{i}}}^{2}+{{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial x_{j}^{i}} \right)}^{2}}m_{x_{j}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial y_{j}^{i}} \right)}^{2}}m_{y_{j}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial x_{A}^{i}} \right)}^{2}}m_{x_{A}^{i}}^{2} \\ &+{{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial y_{A}^{i}} \right)}^{2}}m_{y_{A}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial x_{j}^{0}} \right)}^{2}}m_{x_{j}^{0}}^{2}+{{\left( \frac{\partial ⊿ \Delta x_{j}^{i}}{\partial x_{A}^{0}} \right)}^{2}}m_{x_{A}^{0}}^{2} \\ &m_{⊿ \Delta y_{j}^{i}}^{2}={{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial \Delta {{\alpha }_{i}}} \right)}^{2}}m_{⊿ {{\alpha }_{i}}}^{2}+{{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial x_{j}^{i}} \right)}^{2}}m_{x_{j}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial y_{j}^{i}} \right)}^{2}}m_{y_{j}^{i}}^{2} \\ &+{{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial x_{A}^{i}} \right)}^{2}}m_{x_{A}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial y_{A}^{i}} \right)}^{2}}m_{y_{A}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial y_{j}^{0}} \right)}^{2}}m_{y_{j}^{0}}^{2}+{{\left( \frac{\partial ⊿ \Delta y_{j}^{i}}{\partial y_{A}^{0}} \right)}^{2}}m_{y_{A}^{0}}^{2} \\ &m_{⊿ \Delta z_{j}^{i}}^{2}={{\left( \frac{\partial ⊿ \Delta z_{j}^{i}}{\partial z_{j}^{i}} \right)}^{2}}m_{z_{j}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta z_{j}^{i}}{\partial z_{A}^{i}} \right)}^{2}}m_{z_{A}^{i}}^{2}+{{\left( \frac{\partial ⊿ \Delta z_{j}^{i}}{\partial z_{j}^{0}} \right)}^{2}}m_{z_{j}^{0}}^{2}+{{\left( \frac{\partial ⊿ \Delta z_{j}^{i}}{\partial z_{A}^{0}} \right)}^{2}}m_{z_{A}^{0}}^{2} \\ \end{align} \right. $ | (12) |
因为
| $\begin{gathered} \tan \Delta {\alpha _i} = \tan \left( {\alpha _{AB}^i - \alpha _{AB}^0} \right) = \hfill \\ (\Delta x_B^0\Delta y_B^i - \Delta x_B^i\Delta y_B^0)/(\Delta x_B^0\Delta x_B^i + \Delta y_B^i\Delta y_B^0) \hfill \\ \end{gathered} $ |
所以
| $\begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Delta {\alpha _i} = \hfill \\ {\tan ^{ - 1}}[(\Delta x_B^0\Delta y_B^i-\Delta x_B^i\Delta y_B^0)/(\Delta x_B^0\Delta x_B^i + \Delta y_B^i\Delta y_B^0)] \hfill \\ \end{gathered} $ |
对上式求全微分并转化为中误差式,得:
| $ \begin{gathered} \;\;\;\;\;\;\;\;\;\;\;\;\;\;m_{\Delta {\alpha _i}}^2 = {\left( {\frac{{\partial \Delta {\alpha _i}}}{{\partial \Delta x_B^0}}} \right)^2}\left( {m_{x_B^0}^2 + m_{x_A^0}^2} \right) + \hfill \\ {\left( {\frac{{\partial \Delta {\alpha _i}}}{{\partial \Delta y_B^0}}} \right)^2}\left( {m_{y_B^0}^2 + m_{y_A^0}^2} \right) + {\left( {\frac{{\partial \Delta {\alpha _i}}}{{\partial \Delta x_B^i}}} \right)^2}\left( {m_{x_B^i}^2 + m_{x_A^i}^2} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left( {\frac{{\partial \Delta {\alpha _i}}}{{\partial \Delta y_B^i}}} \right)^2}\left( {m_{y_B^i}^2 + m_{y_A^i}^2} \right) \hfill \\ \end{gathered} $ | (13) |
可结合
可以证明,用支导线法定点时,当令未知点的纵横坐标中误差相等时对未知点的点位中误差大小没有影响[8]。其次,为了公式推导的方便,假设各个监测点在同一次监测时为同精度观测,这同时也符合大多数实际测量工作情况。因此,可以设
| ${m_{x_A^0}} = {m_{x_B^0}} = {m_{y_A^0}} = {m_{y_B^0}} = {m_{x_j^0}} = {m_{y_j^0}} = m_{xy}^0, {m_{z_A^0}} = {m_{z_B^0}} = {m_{z_j^0}} = {m_{{z^0}}}$ | (14) |
| ${m_{x_A^i}} = {m_{x_B^i}} = {m_{y_A^i}} = {m_{y_B^i}} = {m_{x_j^i}} = {m_{y_j^i}} = m_{xy}^i, {m_{z_A^i}} = {m_{z_B^i}} = {m_{z_j^i}} = {m_{{z^i}}}$ | (15) |
式中,mx0或my0为监测点初始值的平面坐标分量中误差;mxi或myi为监测点后次第i次观测时的平面坐标分量中误差;mz0为监测点初始值的高程中误差;mzi为监测点后次第i次观测的高程中误差。
将式 (14)、(15) 分别代入式 (12),并将相应的偏导数代入,化简整理得:
| $\begin{gathered} m_{⊿ \Delta x_j^i}^2 = {\left( {\Delta x_j^i\sin \Delta {\alpha _i} + \Delta y_j^i\cos \Delta {\alpha _i}} \right)^2}m_{\Delta {\alpha _i}}^2 + 2m_{xy}^{{i^2}} + 2m_{xy}^{{0^2}} \hfill \\ m_{⊿ \Delta y_j^i}^2 = {\left( {\Delta x_j^i\cos \Delta {\alpha _i} - \Delta y_j^i\sin \Delta {\alpha _i}} \right)^2}m_{\Delta {\alpha _i}}^2 + 2m_{xy}^{{i^2}} + 2m_{xy}^{{0^2}} \hfill \\ m_{⊿ \Delta z_j^i}^2 = 2(m_{{z^i}}^2 + m_{{z^0}}^2) \hfill \\ \end{gathered} $ |
由式 (8) 可知,在没有发生平面点位位移时,
| $ \left( {\begin{array}{*{20}{c}} {\cos \Delta {\alpha _i}}&{-\sin \Delta {\alpha _i}} \\ {\sin \Delta {\alpha _i}}&{\cos \Delta {\alpha _i}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\Delta x_j^i} \\ {\Delta y_j^i} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\Delta x_j^0} \\ {\Delta y_j^0} \end{array}} \right) $ |
所以
| $\left\{ \begin{gathered} m_{⊿ \Delta x_j^i}^2 = {\left( {\Delta y_j^0} \right)^2}m_{\Delta {\alpha _i}}^2 + 2m_{xy}^{{i^2}} + 2m_{xy}^{{0^2}} \hfill \\ m_{⊿ \Delta y_j^i}^2 = {\left( {\Delta x_j^0} \right)^2}m_{\Delta {\alpha _i}}^2 + 2m_{xy}^{{i^2}} + 2m_{xy}^{{0^2}} \hfill \\ \end{gathered} \right.$ |
顾及式 (13)、式 (14)、式 (15),并代入相应的偏导数化简后得:
| $m_{\Delta {\alpha _i}}^2 = \frac{{2m_{xy}^{{0^2}}}}{{{{\left( {\Delta x_B^0} \right)}^2} + {{\left( {\Delta y_B^0} \right)}^2}}} + \frac{{2m_{xy}^{{i^2}}}}{{{{\left( {\Delta x_B^i} \right)}^2} + {{\left( {\Delta y_B^i} \right)}^2}}}$ |
令两个固定点之间的水平距离为SAB0,则
| $\left\{ \begin{gathered} m_{⊿ \Delta x_j^i}^2 = 2{\left( {\Delta y_j^0} \right)^2}\frac{{m_{xy}^{{0^2}} + m_{xy}^{{i^2}}}}{{{{\left( {S_{AB}^0} \right)}^2}}} + 2m_{xy}^{{i^2}} + 2m_{xy}^{{0^2}} \hfill \\ m_{⊿ \Delta y_j^i}^2 = 2{\left( {\Delta x_j^0} \right)^2}\frac{{m_{xy}^{{0^2}} + m_{xy}^{{i^2}}}}{{{{\left( {S_{AB}^0} \right)}^2}}} + 2m_{xy}^{{i^2}} + 2m_{xy}^{{0^2}} \hfill \\ \end{gathered} \right.$ |
| ${m_{\Delta {\alpha _i}}} = \pm (\sqrt {2(m_{xy}^{{0^2}} + m_{xy}^{{i^2}})} /S_{AB}^0)\rho $ | (16) |
又设初始观测时第j点到A点的距离为SjA0,则
| ${\left( {S_{jA}^0} \right)^2} = {\left( {\Delta x_j^0} \right)^2} + {\left( {\Delta y_j^0} \right)^2}$ |
后次第i次观测时第j点的平面点位位移中误差为
| $M_{d_j^i}^2 = m_{⊿ \Delta x_j^i}^2 + m_{⊿ \Delta y_j^i}^2 = 2\left[{{{\left( {S_{jA}^0/S_{AB}^0} \right)}^2} + 2} \right]\left( {m_{xy}^{{0^2}} + m_{xy}^{{i^2}}} \right)$ |
所以
| ${M_{d_j^i}} = \pm \sqrt {2\left[{{{\left( {S_{jA}^0/S_{AB}^0} \right)}^2} + 2} \right]\left( {m_{xy}^{{0^2}} + m_{xy}^{{i^2}}} \right)} $ |
如果将第j点的初始观测平面点位中误差表示成
| ${M_{d_j^i}} = \pm \sqrt {\left[{{{\left( {S_{jA}^0/S_{AB}^0} \right)}^2} + 2} \right]\left( {m_{d_j^0}^2 + m_{d_j^i}^2} \right)} $ | (17) |
从式 (17) 可以看出,两个固定点A、B之间的距离越大,或者照准点j与A点的距离越小,则平面点位位移的精度就越高,预报得就越准确。因此,在建立观测场时,将固定点A尽可能建在靠近变形体附近的稳定地面上,而只要不影响观测,将固定点B尽可能建在距离变形体较远的稳定地面上。
高程位移中误差的计算公式为:
| $ {m_{⊿ \Delta z_j^i}} = \pm \sqrt {2(m_{{z^i}}^2 + m_{{z^0}}^2)} $ | (18) |
实际应用中可进行多余观测,使初始观测值的精度尽可能提高,甚至可以精确到把初始观测值当作理论值而忽略初始值观测值的误差,即使得
| $\begin{gathered} {M_{d_j^i}} = \pm \sqrt {{{\left( {S_{jA}^0/S_{AB}^0} \right)}^2} + 2} {m_{d_j^i}} \hfill \\ {m_{⊿ \Delta z_j^i}} = \pm \sqrt 2 {m_{{z^i}}} \hfill \\ \end{gathered} $ |
多站观测可以看作是单站观测的集合,只是每一站所观测的点及点数可以不同。
对于一个设站观测不完的变形体,可以进行多设站联测。站与站之间要有一定的重叠观测,其重叠观测的点数不应少于2个,以便将所有监测点在一次监测完成后都统一到一个特定的坐标系中。具体方法如下:
1) 初始观测坐标系的建立。初始观测时,第2设站要重复观测第1设站观测过的两个以上的点,即重叠点,也可以叫拉手点。利用重叠点采用坐标变换方法将第2设站的坐标系统一到第1设站的初始坐标系中。第3设站利用与第2设站的重叠点用同样的方法也统一到第1设站的初始坐标中。依此类推,直到最后一个设站都统一到第1设站的初始坐标中。
2) 后次观测坐标系的建立。后次观测时的情况与1) 类似,不再赘述。后次观测的第1个设站的位置以及照准的点及点数都可以与1) 不同。
一般地,对于建立初始观测坐标系和后次观测坐标系两者所设的站数、各个站的位置、每一站所照准的点数都是可以不同的。对于1)、2) 的实质是利用站与站之间重叠点的坐标变换[9]。
若有多余观测时,还可以进行平差运算,以提高监测精度和发现观测错误。
1.3 单站观测的检核方法对于单设观测,换一个位置设站对两个以上乃至全部点重新观测一次,以达到检核的目的,只要两次观测得到的位移差在一定的精度范围内即可。当然,单站观测还可以采取其他一些检核方法,例如在开始观测前瞄准一个固定点,观测结束后再次瞄准该点,只要两次观测的水平方向和垂直方向之差满足仪器的标称观测精度即可,这同时也能证明在观测期间设站点的稳定情况。为了检核观测时的读数误差和环境变化等影响,可以采用正倒镜观测或多测回观测等观测方法。
2 实际应用和效果分析如图 1所示,在变形体上建立变形监测点7个,编号分别为1、2、3、4、5、6、7(7号点在图中未标出);在稳定地面上建立两个固定点:A和B。
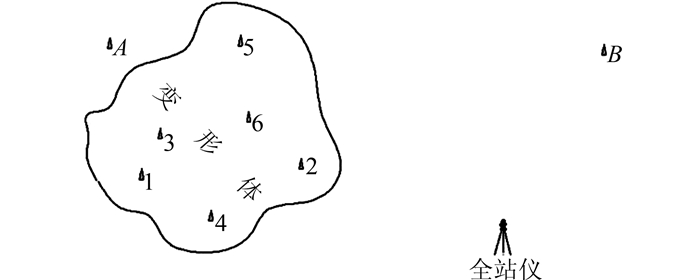 |
| 图 1 变形体观测场示意图 Figure 1 Schematic Diagram of the Deformed Body |
架设全站仪,整平后开机。测量工作开始前,要事先把各种改正参数在全站仪中设置好,例如球气差改正、温度改正、棱镜常数、觇标高等,瞄准各点直接测量其三维坐标。当获取初始观测和后次观测数据后,按式 (8) 计算监测点的位移。
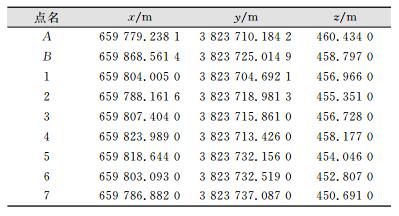
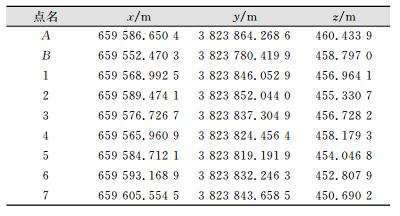
表 1和表 2给出了初始观测数据和后次第6次观测数据,表 3为第6次监测位移计算结果。
| 表 1 初始观测坐标 Table 1 Initial Observation Coordinates |
 |
| 表 2 后次第6次观测坐标 Table 2 After the Sixth Observation Coordinates |
 |
| 表 3 第6次监测位移计算结果 Table 3 Displacement Results of the Sixth Monitoring |
 |
从表 3可知,第6次监测发现2号点发生了明显变化,其三维位移为
由于2号点位于下部不良地质条件地段,因其附近爆破震动影响而发生了位移。其他6个变形监测点在本次监测时没有发现明显位移变化。
3 结束语本文给出了全站仪任意坐标系的三维变形监测方法,与传统方法相比,用于周期性变形监测作业的全站仪设站点不需要固定,并且可以是任何方便的位置,甚至可以建立在变形体上,这种情况下只要保证在一次监测期间设站点的位置不发生变化即可,并且每次监测设站都允许与以前监测时的设站位置不同,每次监测都可以采用不同的三维直角坐标系。本方法利用初始观测坐标系坐标和后次观测坐标系坐标通过坐标变换直接得到位移量,因此既省去了多个外业工作环节,例如设站点的坐标高程不需要已知,不需要后视点,不需要建立观测墩,不需要做控制测量取得各类点的初始值,不需要量取仪器高,不需要全站仪对中等;又容易避开施工干扰,不影响施工,使得外业工作简便、快捷、高效、省时省力;同时也适合于用GPS接收机[10]获取照准点和监测点的初始观测坐标和后次观测坐标的位移计算。
本方法的平面点位位移中误差公式可以指导和优化变形监测的外业布置工作以及提高监测成果的可靠性。
| [1] | 袁恒, 刘成龙, 卢杰, 等. 全站仪三维自由设站隧道非接触监控量测原理及精度分析[J]. 工程勘察, 2012, (8): 63–67. |
| [2] | 杨松林, 刘维宁, 师红云, 等. 全站仪自由设站隧道围岩变形非接触监测理论和方法的研究[J]. 土木工程学报, 2006, 39(4): 100–104. |
| [3] | 杨鹏源. 全站仪在工程变形监测中的应用[J]. 甘肃科学学报, 2009, 21(1): 125–128. |
| [4] | 杨浩. 一种代替测量观测墩的方法[J]. 中国科技论文在线, 2012, 5(18): 1 774–1 779. |
| [5] | 高绍伟, 姜晶, 郭彤. 全站仪自由设站法用于基坑水平位移监测[J]. 工程勘察, 2012, (11): 59–63. |
| [6] | 李又云, 张志耕, 谢永利, 等. 隧道洞顶围岩竖向全位移量测及变化规律研究[J]. 岩土力学, 2013, 34(6): 1 703–1 708. |
| [7] | 马海春, 顾金才, 张向阳, 等. 喷锚支护洞室抗爆现场试验洞顶位移研究[J]. 岩土工程学报, 2012, 34(2): 369–372. |
| [8] |
杨浩.免固定设站点的全站仪三维变形监测方法[P].中国, 201410848192.1[P].2015-03-25 |
| [9] | 许文学, 王保丰, 羊远新, 等. 坐标系转换参数初值快速计算的新方法[J]. 测绘工程, 2010, 19(4): 4–7. |
| [10] | 蓝悦明, 叶玲洁, 汤文娟, 等. GPS技术改造大坝水平位移监测的研究[J]. 测绘地理信息, 2014, 39(1): 8–9. |
 2017, Vol. 42
2017, Vol. 42

