| 北斗IGSO和MEO卫星零偏状态下超快速轨道光压模型 |
2. 武汉大学地球空间信息技术协同创新中心,湖北 武汉,430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan University, Wuhan 430079, China
为了服务于实时用户,国际GNSS(global navigation satellite system)服务组织[1](international GNSS service,IGS)从2000-11-03开始向全球每12 h更新一次GPS超快速轨道产品(分别在00:00和12:00 UTC,并伴有3 h的延迟)。然后,于2004-04-19 IGS将更新频率提高到每6 h一次(增加06:00和18:00 UTC)。中国发起建立的国际GNSS监测评估系统(international GNSS monitoring & assessment system,iGMAS)提供GPS、GLONASS、Galileo和北斗的超快速轨道产品。超快速轨道产品包含前24 h的观测轨道段和后24 h的预报轨道段。轨道预报段采用动力学模型预报的方法实现,即首先采用事后精密轨道拟合得到初始参考时刻精确的卫星轨道状态参数和动力学模型参数,然后基于解算的轨道参数采用动力学积分的方法实现精密轨道预报。
动力学模型中,相较于其他非保守力,太阳光压力对导航卫星轨道产生较大的摄动力。由于光压力的复杂性,受到太阳能量变化、卫星星体表面材质老化、姿态控制误差等多种因素的影响,太阳光压摄动力很难精确模型化,是当前影响导航卫星轨道精度的主要误差源[2]。Beutler等[3]以ROCK模型为先验模型,用9个参数来吸收DYB 3个方向上的常数项和周期项残差,建立了ECOM模型。Springer等[4]进一步开发了ECOM模型,建立了以卫星轨道高度角为函数的6参数模型,称为ECOM 2模型。Bar-Sever等[5, 6]基于ROCK-T模型,采用长期的精密轨道数据进行参数拟合,构建了GSPM模型。Choi等[7]研究了GPS预报轨道策略,发现ECOM 9比ECOM 5参数光压模型得到的预报轨道精度更高,而ECOM 5参数模型具有更稳定的轨道框架旋转参数。半分析半经验型模型介于分析型和经验型模型之间,旨在希望既像分析型模型一样具有实际的物理意义,也能获得经验型模型的高精度轨道。具有代表性的是Rodriguez-Solano等开发的可校正Box-Wing模型[8],该模型可直接校正卫星帆板和星体面板的光学属性参数,能获得和经验型模型相同的轨道确定和预报精度。Rodriguez-Solano等[9]发现在加入卫星偏航姿态后,可校正Box-Wing模型比ECOM 5模型得到的地影时期BLOCK-IIA卫星预报轨道精度更高。
上述光压模型都是在卫星动偏的条件下建立的,然而北斗卫星采取有别于GPS和GLONASS卫星的姿态控制模式,其中,GEO卫星采用零偏模式,IGSO和MEO卫星采用动偏和零偏相互切换的姿态控制模式。IGSO和MEO卫星在轨道角等于90°且高度角小于4°时切换至零偏模式,直至轨道角等于90°且太阳高度角大于4°。由于一天以内太阳高度角的变化小于1°,零偏模式将持续8 d左右[10, 11]。卫星从动偏转换到零偏,其星体受照面将发生变化,传统的光压模型已经不适合该期间的轨道确定和预报。郭靖[10]指出在ECOM 5参数模型中引入约束为1.0×10-10m/s2的切向常量经验加速度能大幅提高北斗IGSO和MEO在零偏时期的定轨精度。然而,在北斗卫星零偏期间,轨道预报中采用的光压模型却几乎没有人研究。本文探讨不同光压模型下,北斗IGSO和MEO卫星在零偏期间轨道预报的表现。由于北斗GEO卫星轨道有较大的未模型化的误差,且GEO卫星因静地特性有频繁的机动调整,所以GEO卫星不在本文的分析中。
1 太阳光压摄动模型在北斗IGSO和MEO零偏时期,为了比较和分析预报轨道的表现,本文共采用ECOM 5参数模型、ECOM 9参数模型、ECOM 5参数加切向经验力模型和修改过后的可校正Box-Wing模型4种不同的光压模型。4种光压模型详细信息如表 1所示。
| 表 1 采用的光压模型总结 Tab.1 Summary of the Adopted Solar Pressure Models |
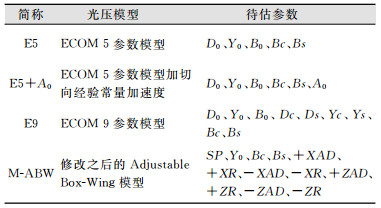 |
本文用ECOM模型中的Bc和Bs参数替代ABW模型中的SB参数来吸收B方向上的残差。同时,添加星体-X面的AD和R参数作为待估参数来吸收-X面由于受照引起的偏差,这种修改过的ABW模型被称为M-ABW模型。
2 实验结果 2.1 数据获取和处理本文选取的数据段是2015年零偏状态下的北斗5颗IGSO和3颗MEO卫星精密轨道(图 1)。图 1右侧的标注为各卫星处于零偏状态的总天数。北斗IGSO和MEO卫星的事后精密轨道由武汉大学卫星导航定位技术研究中心提供[12],这些事后精密轨道不仅是观测拟合轨道,也是评价预报轨道性能的参考轨道。
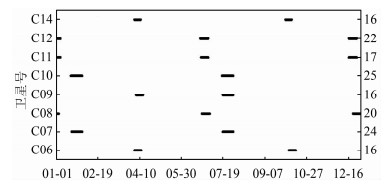 |
| 图 1 北斗IGSO和MEO零偏时期 Fig.1 The Days of BeiDou IGSO and MEO During Yaw-Fixed Mode |
本文以相邻两天48 h的精密轨道作为观测轨道段,首先利用ERP参数将观测轨道段旋转至惯性系下。然后将观测轨道段进行轨道拟合,得到初始时刻的状态参数,包括初始卫星位置、速度和光压参数。最后对初始状态参数进行动力学轨道积分得到24 h的预报轨道。
重力场改正采用EGM 2008 12×12阶,三体引力使用JPL DE405星历文件改正,地球固体潮、极潮、海洋潮汐和相对论效应采用IERS 2010协议改正,考虑地球反照辐射[13]。
对比预报轨道和参考轨道,得到各个时刻卫星径向、法向和切向的轨道差,统计每颗卫星各方向上轨道差的RMS(root mean square)来评价预报轨道的精度:
| $ {\rm{RMS}}_{{\rm{Dir}}}^{{\rm{sat}}} = \sqrt {\frac{{\sum\limits_{{i_{{\rm{epoch}}}} = 0}^{{n_{{\rm{epoch }}}}} {{\mathop{\rm Diff}\nolimits} _{{i_{{\rm{epoch}}}}}^2} {\rm{, Dir}}}}{{{n_{{\rm{epoch}}}}}}{\rm{ }}} $ | (1) |
式中,Diff为轨道差;Sat为卫星号;iepoch为历元数;Dir为卫星各方向。
由于超快速轨道发布有3 h的延迟且每6 h更新一次,所以实时用户用到的往往是超快速产品中第3~9 h的数据,本文统计了预报轨道的3~9 h和整个24 h两个时间段。
2.2 结果分析图 2和图 3分别是北斗IGSO卫星C08和MEO卫星C12预报轨道精度RMS平均值和标准差统计图。从图中可以看出,E5模型在各个方向的RMS平均值和标准差都要明显大于其他模型,特别是切向上的RMS平均值高出其他模型最多可达2 m。在切向上加上常量经验加速度之后,E5+A0模型吸收了由于偏航姿态变化引起卫星切向上的系统性偏差,其轨道预报结果要明显优于E5,尤其是切向上:C08卫星预报24 h的RMS由288 cm提高到144 cm;C12卫星由235 cm提高到113 cm。E9和M-ABW模型轨道预报结果要明显优于E5和E5+A0模型,说明零偏期间卫星在D和Y方向产生了系统性偏差,E9模型在轨道拟合时补足了一定程度上的残差影响。同时,E9和M-ABW模型的精度几乎相当,其中M-ABW模型要略优于E9模型。
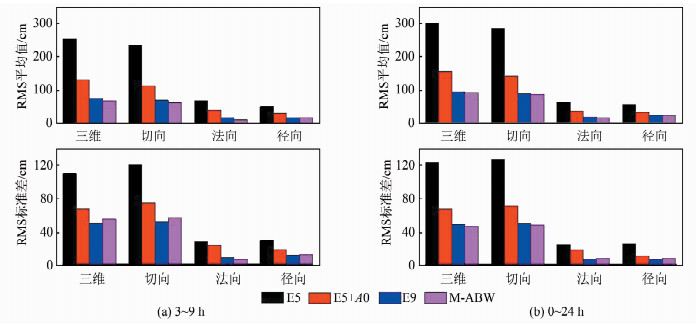 |
| 图 2 北斗IGSO卫星C08在零偏时期预报轨道精度 Fig.2 Accuracy of Predicted Orbits During Yaw-Fixed Mode for BeiDou IGSO-C08 |
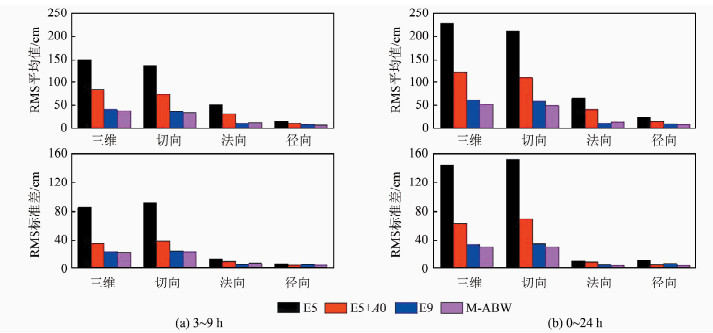 |
| 图 3 北斗MEO卫星C12在零偏时期预报轨道精度 Fig.3 Accuracy of Predicted Orbits During Yaw-Fixed Mode for BeiDou MEO-C12 |
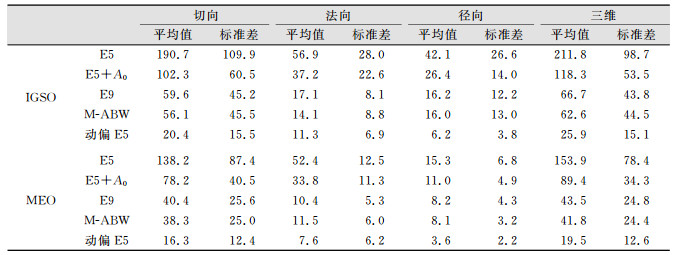
为了进一步分析不同光压模型在零偏状态下的卫星预报轨道性能,本文统计了不同卫星类型在第3~9 h和整个24 h零偏下预报轨道中径向、法向、切向和三维方向RMS的平均值和标准差(表 2和表 3)。与上述分析类似,E9和M-ABW模型不论是对于IGSO还是MEO卫星都是最优的光压模型,E5+A0模型次之,E5模型最差。相较于E9模型,M-ABW预报3~9 h和0~24 h的三维方向RMS精度平均值:IGSO卫星分别提升了4.1 cm和2.1 cm,MEO卫星分别提升了1.7 cm和3.1 cm。但是在RMS稳定性上,M-ABW和E9模型几乎相当。卫星径向精度上,M-ABW和E9相差不超过1 cm。
| 表 2 预报轨道第3~9 h北斗IGSO和MEO卫星的精度统计/cm Tab.2 Precision Statistics of BeiDou IGSO and MEO Satellites for 3-9 h of Predicted Orbits/cm |
 |
| 表 3 预报轨道24 h北斗IGSO和MEO卫星的精度统计/cm Tab.3 Precision Statistics of BeiDou IGSO and MEO Satellites for Whole 24 h of Predicted Orbits/cm |
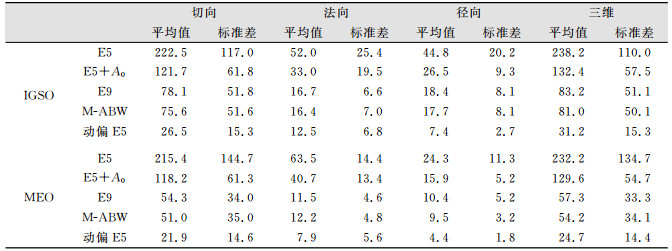 |
表 2和表 3包含了IGSO和MEO卫星在动偏期间轨道预报结果,可以对比动偏时期轨道预报的精度。动偏时间选择2015-03,光压模型为E5模型[14]。为了和零偏期间保持一致,本文同样用48 h的观测轨道预报得到24 h的预报轨道。从表中可以看出,零偏时期M-ABW模型得到的结果和动偏时期的预报结果最为接近,其次是E9模型。对于IGSO和MEO卫星,动偏下M-ABW模型三维方向的精度和E5模型分别相差35~50 cm和25~30 cm,其中切向差异最大,其次是径向。说明在零偏期间由于姿态变化引起的未模型化的误差仍然较大。
0~24 h的RMS整体大于3~9 h的RMS,其原因是预报轨道的精度会随着时间的增加而下降。值得注意的是,相较于MEO卫星,不同光压模型对于IGSO卫星轨道预报的影响明显更大,可能是因为IGSO卫星的轨道高度更高,受到太阳光压的影响更大;IGSO卫星运动缓慢,定轨几何构型较差,观测轨道精度略低于MEO卫星的也是原因之一。
2.3 SLR外部检核由于卫星激光测距(satellites laser ranging, SLR)能够提供高精度的距离信息,常作为导航卫星轨道的独立检核手段。北斗卫星装备有激光反射棱镜,支持地面站对其进行激光测距。比较国际激光测距服务组织(international laser ranging service, ILRS)提供的SLR观测值和预报轨道计算得到的星地距,可以得到SLR观测值残差。统计残差的RMS值可以作为卫星预报轨道的径向精度。
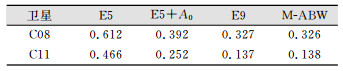
本文对北斗IGSO卫星C08和MEO卫星C11零偏时期进行SLR外部检核,C08和C11卫星的激光标准点个数分别是36和40,其中大于2 m的残差将被认为是粗差而剔除。表 4是各个光压模型预报轨道SLR残差的RMS。从表 4可以看出,SLR外部检测的结果和§2.2中的分析几乎一致。E9和M-ABW模型SLR残差的RMS最小,两者精度相当,相较于E5模型,C08卫星提高了47.5%,C11卫星提高了71.7%,相较于E5+A0模型,C08卫星提高了17.9%,C11卫星提高了47.6%。
| 表 4 北斗C08和C11卫星零偏期间预报轨道SLR残差的RMS/m Tab.4 RMS of SLR Residuals for BeiDou C08 and C10 Predicted Orbits During Yaw-Fixed Mode/m |
 |
3 结束语
本文采用2015年全年北斗IGSO和MEO零偏的数据实现轨道预报,比较4种光压模型在零偏时期轨道预报的表现,包括ECOM 5参数模型、ECOM 5参数加切向常量经验加速度模型、ECOM 9参数模型和修改过的Adjustable Box-Wing模型。其预报轨道和事后精密星历、SLR观测值相比较得出:不论是对于北斗IGSO还是MEO卫星,ECOM 9参数和修改过的Adjustable Box-Wing模型的精度和稳定性是最优的,其中修改过的Adjustable Box-Wing模型略优于ECOM 9参数模型;和动偏期间轨道预报相比,零偏期间需要提高的主要是切向和径向方向上的精度。
| [1] |
Dow J M, Neilan R E, Rizos C. The International GNSS Service in a Changing Landscape of Global Navigation Satellite Systems[J]. Journal of Geodesy, 2009, 83(3/4): 191-198. |
| [2] |
车通宇, 杨力, 张传定, 等. SDP4模型用于北斗导航卫星轨道预报的精度分析[J]. 测绘地理信息, 2017, 42(2): 12-16. |
| [3] |
Beutler G, Brockmann E, Gurtner W, et al. Extended Orbit Modeling Techniques at the CODE Processing Center of the International GPS Service for Geodynamics (IGS): Theory and Initial Results[J]. Eurpean Respiratory Journal, 1994, 19: 367-386. |
| [4] |
Springer T A, Beutler G, Rothacher M. A New Solar Radiation Pressure Model for GPS Satellites[J]. GPS Solutions, 1999, 2(3): 50-62. DOI:10.1007/PL00012757 |
| [5] |
Bar-Sever Y, Kuang D. New Empirically Derived Solar Radiation Pressure Model for Global Positioning System Satellites[R]. IPN Progress Report, 42-159, Jet Propulsion Laboratory, Pasadena, CA, 2004
|
| [6] |
Bar-Sever Y, Kuang D. New Empirically Derived Solar Radiation Pressure Model for Global Positioning System Satellites During Eclipse Seasons[R]. IPN Progress Report, 42-160, Jet Propulsion Laboratory, Pasadena, CA, 2004
|
| [7] |
Choi K K, Ray J, Griffiths J, et al. Evaluation of GPS Orbit Prediction Strategies for the IGS Ultra-Rapid Products[J]. GPS Solutions, 2013, 17(3): 403-412. DOI:10.1007/s10291-012-0288-2 |
| [8] |
Rodriguez-Solano C J, Hugentobler U, Steigenberger P. Adjustable Box-Wing Model for Solar Radiation Pressure Impacting GPS Satellites[J]. Advance in Space Research, 2012, 49: 1 113-1 128. DOI:10.1016/j.asr.2012.01.016 |
| [9] |
Rodriguez-Solano C J, Hugentobler U, Steigenberger P, et al. Improving the Orbits of GPS Block ⅡA Satellites During Eclipse Seasons[J]. Advance in Space Research, 2013, 52(8): 1 511-1 529. DOI:10.1016/j.asr.2013.07.013 |
| [10] |
郭靖.姿态、光压和函数模型对导航卫星精密定轨影响的研究[D].武汉: 武汉大学, 2014
|
| [11] |
Montenbruck O, Schmid R, Mercier F, et al. GNSS Satellite Geometry and Attitude Models[J]. Advance in Space Research, 2015, 56(6): 1 015-1 029. DOI:10.1016/j.asr.2015.06.019 |
| [12] |
Rodriguez-Solano C J, Hugentobler U, Steigenberger P. Impact of Albedo Radiation on GPS Satellites[J]. In Proceedings of Geodesy for Planet Earth, 2012, 136: 113-119. |
| [13] |
Guo J, Xu X, Zhao Q, et al. Precise Orbit Determination for Quad-Constellation Satellites at Wuhan University: Strategy, Result Validation, and Comparison[J]. Journal of Geodesy, 2016, 90(2): 143-159. DOI:10.1007/s00190-015-0862-9 |
| [14] |
Guo F, Li X, Zhang X, et al. Assessment of Precise Orbit and Clock Products for Galileo, BeiDou, and QZSS from IGS Multi-GNSS Experiment (MGEX)[J]. GPS Solutions, 2017, 21(1): 279-290. DOI:10.1007/s10291-016-0523-3 |
 2020, Vol. 45
2020, Vol. 45

