| 分级统计地图的模型评价与应用 |
2. 浙江省测绘科学技术研究院, 浙江 杭州, 310012
2. Zhejiang Academy of Surveying and Mapping, Hangzhou 310012, China
分级统计地图是按照行政区划或自然区划,以疏密不同的点纹、线纹或深浅不一的颜色反映各区划现象的密度、强度等指标的统计地图[1]。它通过分级将比率量表转为间隔量表,使区划间的数量差异转为图形差异,从而赋予地图更强的表现力和感知力。
分级统计地图的编制主要包括两个方面:一是数据分级与精度评价,二是制图单元的填充。就分级而言,现有的研究成果是以反映数据分布特征的模型构建为重点[2-4]。就精度评价而言,文献[5]最早提出了基于网格精度指数(tabular accuracy indices, TAI)、边界精度指标(boundary accuracy index, BAI)、总体精度指标(overview accuracy in dex, OAI)的三维尺度评价分级精度的方法,文献[6]利用最大内部均匀性分级(maximum internal uniformity classification,MIUC)评价级内集中度(internal degree of concentration, IDC),文献[7]提出了一种用级内数据最值反映级间离散度并结合TAI来评价分级精度的方法,文献[8]在文献[7]的基础上,结合分级信息量等属性来评价分级精度。
就制图单元填充而言,目前有两种方式,一是基于已有的图形处理软件进行手工操作,这种方式费时费力,不利于制图效率的提高,二是基于GIS平台进行开发[9],但目前基于该类平台生成的地图较难满足出版的要求。虽然CorelDRAW凭借其超强的图形编辑、整饰功能以及易开发性深受制图人员的喜爱,但目前为止,在CorelDRAW环境下自动生成分级统计地图还没有得到很好的解决。
为此,在深入分析多种分级模型的基础上,本文提出了一种用级内数据集中度和级间均值离散度评价分级精度的方法。同时,在CorelDRAW环境下进行了二次开发,实现了分级统计地图从统计数据分级到面状符号填充等一系列过程的自动化。
1 面状符号类型就分级统计地图而言,面状符号包括点纹、线纹、混合纹、底色4种类型[10]。①点纹符号主要利用点符号的疏密来反映区划间不同等级的指标,点纹填充分有损和无损两种; ②线纹符号主要利用线的粗细、间距来反映区划间不同等级的指标,线纹填充有调频型和调幅型两种; ③点纹符号和线纹符号的组合即为混合纹符号,混合纹有三种组合方式,分别为点-点组合、点-线组合、线-线组合; ④底色的使用可以使其与地图其他要素相分离,形成不同层次的视觉形态,可大大提高地图的表现力和信息量[10]。当使用系统渐变色填充制图单元时,各级填充色的RGB分量为:
| $ \left\{ \begin{array}{l} {R_i} = {R_1} + \frac{{{R_n}-{R_1}}}{{n-1}}\left( {i-1} \right)\\ {G_i} = {G_1} + \frac{{{G_n} - {G_1}}}{{n - 1}}\left( {i - 1} \right)\\ {B_i} = {B_1} + \frac{{{B_n} - {B_1}}}{{n - 1}}\left( {i - 1} \right) \end{array} \right. $ | (1) |
式中,Ri、Gi、Bi为第i级填充色的RGB分量; R1、G1、B1和Rn、Gn、Bn分别为渐变色的首尾RGB分量。
2 数据分级理论阐述分级理论之前,先定义一些概念:X为从小到大的有序数据集合,N为X中的数据个数,X为X的均值,xi为X的第i个数据,Xi为第i级数据集合,xij为第i级第j个数据,Xi为第i级数据的均值,Ni为第i级数据个数,X′为级均值的平均值,n为分级数,F()为级内数据集中度的度量函数,G()为级间数据离散度的度量函数。
数据分级有两种规则,一是根据行业规范进行分级; 二是自定义分级,即根据级内不能为空,级间不能重叠; 级内差异最小,级间差异最大两个原则,将数据归置到各等级内。本文在文献[11]的基础上,对自定义分级的数学定义进行了拓展为:
| $ \left\{ \begin{array}{l} X = { \cup _{i \in I}}{X_i}, \forall i \in I, {X_i} \in X\\ {X_i} \ne \emptyset, \forall i \in I\\ {X_i} \cap {X_j} = \emptyset, \forall \left( {i, j} \right) \in I \times I, i \ne j\\ \sum\limits_{i = 1}^n {F\left( {{X_i}, {n_i}} \right) = \min } \\ G\left( {{X_1}, {X_2}, \cdots, {X_n}} \right) = \max \end{array} \right. $ | (2) |
数据分级有三个过程:分级数的确定,分级界限的确定,分级精度的评价。
2.1 分级级数分级数越大,对数据的综合程度就越小,分级精度就越高,但人眼能辨别的等级差别有限,这就得限制分级数不能太大[12]。总体而言,分级数的确定与多种因素(地图用途、制图单元数、数据分布特征以及面状符号类型等)有关,其值一般定为3~7级。
2.2 分级模型根据数据的利用程度,分级模型可分为基于数学规则的、基于数据特征值的、基于数据分布特征的3类模型。
1) 基于数学规则的分级模型。分级界限可用数学表达式计算得到的分级模型即为基于数学规则的分级模型,该类模型主要利用数据的最值或个数。具体有界限等差、间隔等差、界限等比、间隔等比、分位数等。
2) 基于数据特征值的分级模型。所谓特征值即反映数据总体分布特征的值,如平均值、方差、标准差等。利用这些特征值进行分级就是基于数据特征值的分级模型。正态分级属于该类分级模型。
3) 基于数据分布特征的分级模型。该类分级模型注重局部数据的分布特征,即突出级内集中度与级间离散度。动态聚类、最优分割[13]、弱最优分割[7]等都属于该类分级模型,本文重点探讨动态聚类。文献[2]认为动态聚类对初始聚类中心有一定要求,不合理的初始聚类中心会导致某些等级无数据。
为解决上述问题,本文给出了一种初始聚类中心的计算方法:首先,对X中相邻数据进行作差(xi+1-xi),并对差值进行从小到大排序得D={d1, d2, d3, …, dm-1}; 然后,在X中取得与{dm-n+1, dm-n+2, dm-n+1, …, dm-1}对应的数据xk1, xk1+1, xk2, xk2+1, …, xkn-1, xkn-1+1,其中xk1+1-xk1=dm-n+1, xk2+1-xk2=dm-n+2, …; 接着,计算分级界限B,即b0=x1,bi= xki+xki+1 /2,bn=xm; 最后, 根据B计算{X1, X2, X3, …, Xn},进而计算级均值{X1, X2, X3, …, Xn},即为初始聚类中心。在众多分级模型中,分级精度决定了该选哪种模型进行分级。
2.3 分级精度由式(2)可知,评价分级精度的根本就是寻找F函数和G函数来度量级内集中度(IDC)和级间离散度。
1) 利用F函数度量级内集中度。文献[14]利用离差平方和
| $ {\rm{DCI}} = \sum\limits_{i = 1}^n {\frac{1}{{{{\bar X}_i}}}\sqrt {\sum\limits_{j = 1}^{{n_i}} {{{\left( {{x_{ij}} - {{\bar X}_i}} \right)}^2}} } } $ | (3) |
IDC值越小,表明级内越集中。
2) 利用G函数度量级间离散度。文献[7]利用级内数据的最值来度量级间离散度。但文献[16]认为级均值才是各等级的最佳代表值,这表明级均值的离散度(mean dispersion, MD)可以间接反映级间离散度。由此,本文利用开方的相对离差平方和来度量级均值离散度,从而反映MD,公式为:
| ${\rm{MD}} = \frac{1}{{\bar X'}}\sqrt {\sum\limits_{i = 1}^n {{{\left( {{{\bar X}_i} - \bar X'} \right)}^2}} } $ | (4) |
MD值越大,表明级间越离散。
3) 分级精度评价。通过将G函数与F函数做除法,可综合地评价分级精度σ,公式为:
| $\sigma = \left\{ {\begin{array}{*{20}{l}} {{\rm{MD}}/{\rm{IDC}},\;\;{\rm{IDC}} \ne 0}\\ {\infty ,\;\;{\rm{IDC}} = 0\;} \end{array}} \right.$ | (5) |
σ越大,分级精度越高。
3 分级统计地图分级统计地图的自动构建(不考虑地理底图)分为统计数据获取、统计数据分级、制图单元填充3步。构建流程如图 1所示。
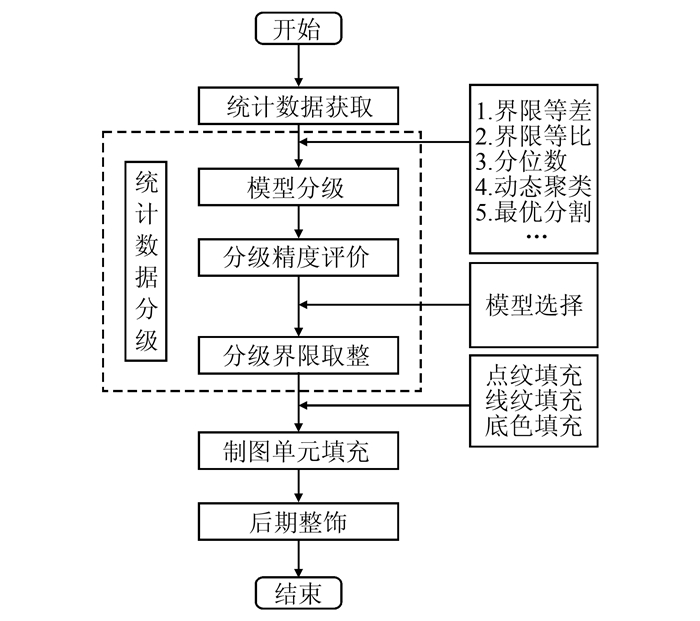 |
| 图 1 分级统计地图构建流程 Figure 1 Generation Process of Choroplethic Maps |
3.1 统计数据分级
计算机分级过程分为两步,一是分级模型选择,二是分级界限取整。本文数据来源于湖北省统计局官网的2010年第六次全国人口普查湖北省各县市常住人口。
1) 分级模型的选择。本文对多种分级模型进行了对比,如图 2所示(n=5)。
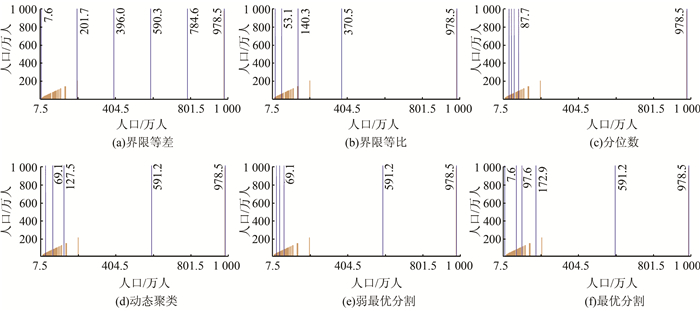 |
| 图 2 各模型的分级结果 Figure 2 Classification Results of Various Models |
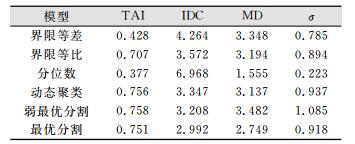
由表 1可得,就TAI值而言,最优分割、动态聚类、弱最优分割3者相差不大,较难从中选其一。但就σ值而言,弱最优分割比另外两种分级模型高。因此,该统计数据适合用弱最优分割进行分级。
| 表 1 分级精度评价 Table 1 Precision Evaluation of the Classification |
 |
2) 分级界限取整。从图 2(e)中可看出,弱最优分割分级后的分级界限是杂乱的浮点值,而具有规则的或者取整的分级界限不仅利于记忆,还利于制图信息的表达,所以还需进行分级界限取整。
3.2 制图单元填充分级完毕后,就可进行制图单元填充。具体包括点纹填充、线纹填充、底色填充。至于混合纹,究其根本是前两者的组合。
3.2.1 点纹填充点纹填充包括有损和无损两种。
1) 有损点纹填充的基本思想是:通过点符号调和生成覆盖制图单元的点纹符号,将其与制图单元相交即可实现有损填充。设制图单元M的外接矩形ABCD的高为h,宽为w,g为相邻点符号的间距,则点符号的行数n1和列数n2为:
| $ \left\{ \begin{array}{l} {n_1} = \left[{{h / g}} \right] + 2\\ {n_2} = \left[{{w / g}} \right] + 2 \end{array} \right. $ | (6) |
4个调和点组成矩形A′B′C′D′,其高度h′和宽度w′为:
| $\left\{ \begin{array}{l} h' = \left( {{n_1} - 1} \right) \cdot \;g\\ w' = \left( {{n_2} - 1} \right) \cdot \;g \end{array} \right.$ | (7) |
结合M的中心点O点坐标就可计算点A′、B′、C′、D′在CorelDRAW中的坐标。
填充步骤如下:①利用CenterX和CenterY属性获得M的中心点O的坐标(xO,yO),并利用式(6)和式(7)计算调和点A′、B′、C′、D′的坐标。②首先,利用Duplicate函数将点符号分别复制到A′、B′、C′、D′四个点上; 然后,利用CreateBlend函数对A′、B′上的点符号进行调和,生成线状点纹s1,对C′、D′点上的点符号进行调和,生成线状点纹s2,其调和数均为n2-2;最后,对s1和s2进行调和,调和数为n1-2,得覆盖矩形A′B′C′D′的点纹S。③将S中所有的线状点纹错开排列,并利用Intersect函数将S与M进行相交生成点纹符号S′,有损填充完毕,如图 3(a)所示。
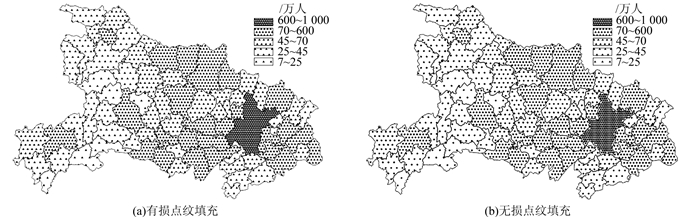 |
| 图 3 有损和无损填充的分级统计图 Figure 3 Choroplethic Maps of Loss and Lossless Filling |
2) 无损点纹填充的基本思想是:首先,对制图单元M进行轮廓内向偏移生成M′; 然后,利用微小圆对M′进行有损填充; 最后,利用点符号逐个替换这些微小圆,实现无损填充。
填充步骤如下:①利用CreateContour函数对M进行轮廓内向偏移(偏移距离为点符号外接矩形的外接圆半径),生成M′; ②利用半径为0.001 mm的微小圆对M′进行有损填充; ③利用Duplicate函数将点符号逐个复制到微小圆上,并删除这些微小圆,从而实现无损填充,如图 3(b)所示。
3.2.2 线纹填充线纹填充分为调频型与调幅型两种。
1) 调频型线纹填充的基本思想是:通过线符号调和,生成覆盖制图单元的线纹,然后将其与制图单元相交,即可实现线纹填充。设制图单元M的外接矩形的外接圆半径为R,g为线距,则覆盖正方形ABCD的线符号数量n为:
| $ n = \left[{2R/g} \right] + 2 $ | (8) |
正方形ABCD的边长d为:
| $d = \left( {n - 1} \right) \cdot \;g$ | (9) |
结合O点坐标就可计算调和点A、B、C、D在CorelDRAW中的坐标。
填充步骤如下:①首先,利用CenterX和CenterY属性获得M的中心点O的坐标(xO,yO); 然后,利用SizeHeight和SizeWidth属性获得M的外接矩形高度和宽度,并计算该外接矩形的外接圆半径R; 最后,利用式(8)和式(9)计算A、B、C、D四点的坐标。②绘制AB直线L1和DC直线L2; 利用CreateBlend函数对L1和L2进行调和,调和数为n-2,生成覆盖正方形ABCD的线纹符号P; 将P旋转指定角度。③利用Intersect函数对P与M进行相交处理,得面状符号P′,实现调频型线纹填充,如图 4(a)所示。
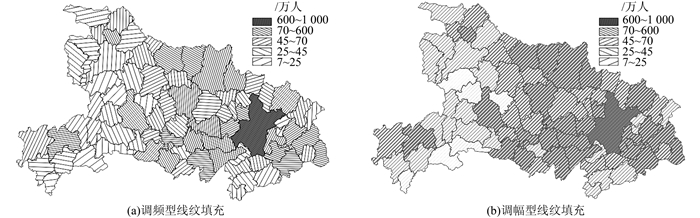 |
| 图 4 调频型和调幅型线纹填充的分级统计图 Figure 4 Choroplethic Maps of FM and AM Lines Filling |
2) 调幅型线纹填充的原理与调频型一致,但在填充时,需将上述步骤中线符号L1和L2替换为矩形条,矩形长与线长相等,矩形宽与线宽相等,其目的是避免因线符号太宽而造成线纹与制图单元边界的相交处出现锯齿状,如图 4(b)所示。
3.2.3 底色填充为了方便设色,本文提供了两套设色工具,一是利用预制的渐变色条; 二是利用ColorDialog颜色控件进行自定义设色。若使用渐变色条设色,则利用式(1)计算各级颜色的RGB分量。结果如图 5所示。
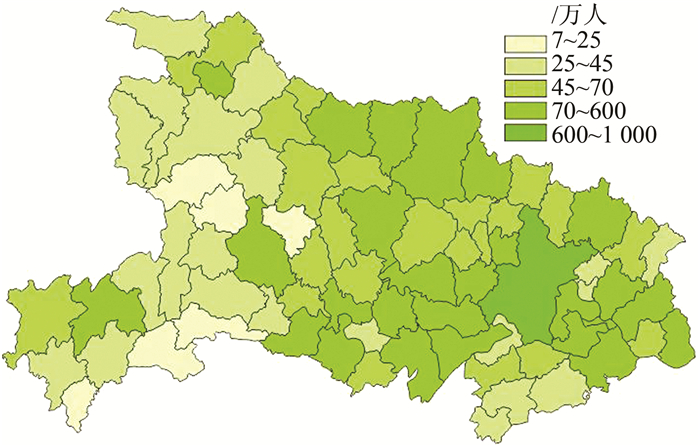 |
| 图 5 底色填充的分级统计地图 Figure 5 Choroplethic Map of Background Color Filling |
4 结束语
本文从理论、技术、应用3个层面对分级统计地图的精度评价与自动生成进行了探究。在理论上,从点纹、线纹、混合纹、底色4个方面归纳了分级统计地图的面状符号类型。同时,从统计数量的利用程度角度对分级模型进行了分类,给出了动态聚类初始聚类中心的计算方法,并提出了一种用级内数据集中度和级间均值离散度来评价分级精度的方法。在技术上,基于CorelDRAW环境进行了二次开发,实现了统计数据的模型分级、评价和选择,点纹符号的有损与无损填充、线纹符号的调频型与调幅型填充、底色符号的渐变色与自定义色填充。在应用上,对提高统计地图制图水平和效率具有现实意义。
| [1] | 黄仁涛, 庞小平, 马晨燕. 专题地图编制[M]. 武汉: 武汉大学出版社, 2003 |
| [2] | 党安荣. 动态聚类方法在单指标专题要素分级中的应用[J]. 陕西师范大学学报(自科版), 1988, 16(3): 71–75, 91 |
| [3] | 党安荣. 统计地图分级方案的分析研究[J]. 测绘科学, 1988, (4): 10–17 |
| [4] | Armstrong M R, Xiao Ningchuan, Bennett D A. Using Genetic Algorithms to Create Multicrieria Class Intervals for Choropleth Maps[J]. Annals of the Association of American Geographers, 2015, 93(3): 595–623 |
| [5] | Jenks G F, Caspall F C. Error on Choroplethic Maps: Definition, Measurement, Reduction[J]. Annals of the Association of American Geographers, 1971, 61(2): 217–244 DOI: 10.1111/j.1467-8306.1971.tb00779.x |
| [6] | 陆效中. 统计地图分级的一般原则和定量标准的探讨[J]. 军测科技, 1987, (1): 10–18 |
| [7] | 孙亚梅, 王如云. 专题要素分级的新方法及其应用[J]. 测绘学报, 1994, 23(1): 59–65 |
| [8] | 江南, 白小双, 孙娟娟. 基于多属性决策的统计数据分级评价模型[J]. 测绘学报, 2007, 36(2): 198–202 |
| [9] | 章莉萍, 郭庆胜. 网络上分级统计地图制图软件的设计与开发[J]. 测绘信息与工程, 2006, 31(3): 47–49 |
| [10] | 钟业勋, 胡毓钜, 吴剑辉. 地图要素分类的定义及其度量化研究[J]. 测绘工程, 1999, 8(2): 11–12 |
| [11] | 俞连笙, 王涛. 地图整饰[M]. 2版. 北京: 测绘出版社, 1995 |
| [12] | 祝国瑞. 地图学[M]. 武汉: 武汉大学出版社, 2004 |
| [13] | 杨永国. 数学地质[M]. 滁州: 中国矿业大学出版社, 2010 |
| [14] |
[14] 孙娟娟.专题地图数据分级模型的研究[D].郑州: 信息工程大学, 2007 http://cdmd.cnki.com.cn/Article/CDMD-90008-2008044430.htm |
| [15] | 沈建法, 黄叶芳. 一类新的最优分割法及其应用[J]. 数学的实践与认识, 1989, (2): 51–52 |
| [16] | 陆效中. 具有最大内部均匀性的规则分级间隔[J]. 地图, 1987, (1): 12–13 |
 2017, Vol. 42
2017, Vol. 42

