| 不确定性平差算法在沉降灰色模型中的应用 |
目前,处理沉降数据[1-4]的方法大多依据随机误差的特点建立高斯马尔科夫模型,进行平差解算。而测量数据中往往包含许多不确定的先验信息或附加信息(其统计信息和概率分布函数无法确定)[5, 6],建立的函数模型常出现病态现象[7, 8]。有学者运用整体最小二乘的平差方法处理此类病态问题[9, 10],但考虑到整体最小二乘平差模型将不确定性同时融入观测矩阵和系数矩阵,可能导致系数矩阵过度修正[11]。还有研究将先验信息转化成等式或者不等式约束[12-23],应用于GPS、导航以及变形监测模型的建立,等式和不等式约束虽然可以更好地描述观测对象的几何和物理力学性质,建立相关的约束平差模型容易,但对于一些以范围、集合形式出现的复杂先验信息却无能为力。本文通过研究变形数据的特点,基于时间序列将参数的不确定度融入灰色GM(1, 1)模型。在解算过程中,通过限制不确定性从而计算出灰色模型中的参数,通过比较预测结果与实测数据之间的差异,分析了在灰色模型中降低不确定性的影响,以提高灰色模型的有效性。
1 灰色GM(1, 1)模型设沉降原始监测序列为:
| $ {\mathit{\boldsymbol{x}}^{\left( 0 \right)}} = \left\{ {{\mathit{\boldsymbol{x}}^{\left( 0 \right)}}\left( 1 \right),{\mathit{\boldsymbol{x}}^{\left( 0 \right)}}\left( 2 \right), \cdots ,{x^{\left( 0 \right)}}\left( m \right)} \right\} $ | (1) |
将原观测序列转化为1-AGO列,即累加序列
| $ {\mathit{\boldsymbol{x}}^{\left( 1 \right)}} = \left\{ {{\mathit{\boldsymbol{x}}^{\left( 1 \right)}}\left( 1 \right),{\mathit{\boldsymbol{x}}^{\left( 1 \right)}}\left( 2 \right), \cdots ,{\mathit{\boldsymbol{x}}^{\left( 1 \right)}}\left( m \right)} \right\} $ | (2) |
式中,
生成紧邻均值序列
| $ {z^{\left( 1 \right)}} = \left\{ {{z^{\left( 1 \right)}}\left( 1 \right),{z^{\left( 1 \right)}}\left( 2 \right), \cdots ,{z^{\left( 1 \right)}}\left( m \right)} \right\} $ | (3) |
式中,
建立GM(1, 1)模型,有:
| $ {\mathit{\boldsymbol{x}}^{\left( 0 \right)}}\left( k \right) + a{z^{\left( 1 \right)}}\left( k \right) = u $ | (4) |
式中,a、u为待估参数,按最小二乘平差模型得:
| $ \mathit{\boldsymbol{\hat x}} = \left[ {\begin{array}{*{20}{c}} a\\ u \end{array}} \right] = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (5) |
式中,
GM(1, 1)模型的白化形式为
| $ \frac{{{\rm{d}}{x^{\left( 1 \right)}}}}{{{\rm{d}}t}} + a{x^{\left( 1 \right)}} = u $ | (6) |
解出a,u后,再根据1-AGO序列与原始观测序列的关系,有边界条件
| $ {x^{\left( 1 \right)}}\left( 1 \right) = {x^{\left( 0 \right)}}\left( 1 \right) $ | (7) |
得到GM(1, 1)模型的离散响应:
| $ {{\hat x}^{\left( 1 \right)}}\left( {k + 1} \right) = \left[ {{x^{\left( 0 \right)}}\left( 1 \right) - \frac{u}{a}} \right]{e^{ - ak}} + \frac{u}{a} $ | (8) |
还原观测序列,则有:
| $ {{\hat x}^{\left( 0 \right)}} = \left\{ {{{\hat x}^{\left( 0 \right)}}\left( 2 \right),{{\hat x}^{\left( 0 \right)}}\left( 3 \right), \cdots ,{{\hat x}^{\left( 0 \right)}}\left( m \right)} \right\} $ | (9) |
式中,
沉降观测数据常常存在一些不确定的附加信息或先验信息,其统计信息和概率分布函数无法确定。如对于某一次沉降观测值xi,其干扰量Δxi是带有某一限定区间信息,即
| $ {a_i} \le \Delta {x_i} \le {b_i},i = 1,2, \cdots ,n $ | (10) |
此时,式(5)中B、L的干扰量ΔB、ΔL就是带有不确定性的矩阵和向量,可以用2-范数形式表达这种不确定性:
| $ {\left\| {\Delta \mathit{\boldsymbol{B}}} \right\|_2} \le \alpha ;{\left\| {\Delta \mathit{\boldsymbol{L}}} \right\|_2} \le \beta $ | (11) |
在平差模型中融入不确定度参数α和β,于是成为带不确定性的平差模型:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}} = \left( {\mathit{\boldsymbol{B}} + \Delta \mathit{\boldsymbol{B}}} \right)\mathit{\boldsymbol{X}}}\\ {{{\left\| {\Delta \mathit{\boldsymbol{B}}} \right\|}_2} \le \alpha ;{{\left\| {\Delta \mathit{\boldsymbol{L}}} \right\|}_2} \le \beta } \end{array}} \right. $ | (12) |
在带不确定性的平差模型中,不确定度α和β的上限已知,即系数矩阵B和观测向量L的不确定性是已知的;在整体最小二乘平差(total least-square,TLS)中,系数矩阵和观测向量的不确定性是未知的;最小二乘平差(least-square,LS)中没有系数矩阵的不确定性(即ΔB=0),观测向量的不确定性未知。
对ΔB和ΔL的不确定性进行参数估计,可根据文献[5]给出的min-max平差准则,让残差的最大不确定性达到最小,即
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{\hat x} \;\;\;\;\;\mathop {\max }\limits_{{{\left\| {\Delta B} \right\|}_2} \le \alpha ;{{\left\| {\Delta L} \right\|}_2} \le \beta } }\\ {\left\{ {{{\left\| {\left( {\mathit{\boldsymbol{L}} + \Delta \mathit{\boldsymbol{L}}} \right) - \left( {\mathit{\boldsymbol{B}} + \Delta \mathit{\boldsymbol{B}}} \right)\mathit{\boldsymbol{\hat x}}} \right\|}_2}} \right\}} \end{array} $ | (13) |
在此准则下的一个岭估计为:
| $ \mathit{\boldsymbol{\hat x}} = {\left( {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} + \mu \mathit{\boldsymbol{I}}} \right)^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{L}} $ | (14) |
岭参数μ的计算方法参见文献[5]。
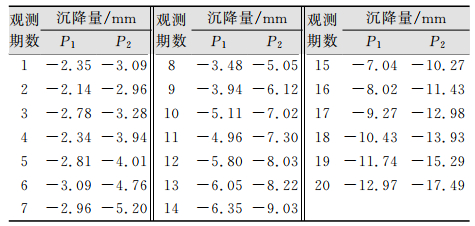
3 实例分析本文研究的观测数据为某一建筑物中两个监测点各20期的沉降数据,如表 1所示。选取其中前13期数据建立灰色GM(1, 1)模型,分别采用一般最小二乘平差(LS)、整体最小二乘平差(TLS)以及带不确定性的平差(ULS)(其中α、β的选取,根据对同一观测点前后两次的观测高差不超过±0.5 mm,认为前一次数据是可靠的规定,确定每期观测沉降量的不确定度为0.5,于是有‖ΔB‖2≤α=2.0,‖ΔL‖2≤β=2.0)计算灰色GM(1, 1)模型中的参数a,u。并预测后7期沉降量,将预测值与实测值对比,分析带不确定性的平差算法(ULS)在沉降GM(1, 1)模型中的作用以及与最小二乘平差(LS)和整体最小二乘平差(TLS)相比的优势。
| 表 1 沉降观测数据 Tab.1 Settlement Observation Data |
 |
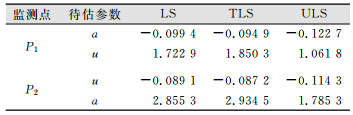
利用监测点P1和P2的沉降数据分别建立的沉降GM(1, 1)模型,由3种平差方法求得的待估参数a、u如表 2所示。
| 表 2 GM(1, 1)模型待估系数 Tab.2 Unknown Parameters in GM(1, 1) Model |
 |
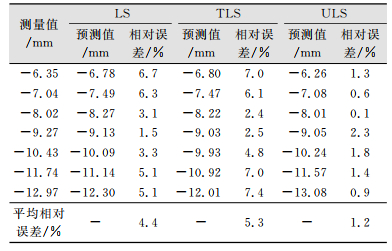
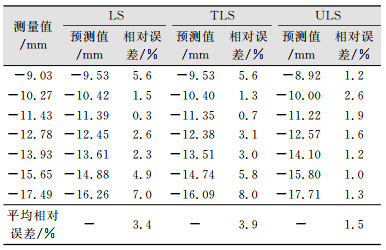
从监测点P1(表 3)和P2(表 4)的后7期沉降预测结果的平均相对误差可以看出,整体最小二乘平差(TLS)由于系数矩阵和观测向量同时考虑不确定性,但这种不确定性的限度未知,导致了修正过度,使得结果不及一般最小二乘平差(LS),在两个监测点的预测结果相对误差都较大。而本文的不确定性平差算法(ULS),充分考虑了不确定的先验信息,在系数矩阵和观测向量中都加以限制,得到的结果优于前两种平差方法,监测点P1和P2预测结果的平均相对误差分别为1.2%和1.5%。图 1和图 2(预测曲线、实测曲线比较)同样直观地表明了不确定性平差算法(ULS)计算的后7期预测结果曲线与实测数据更为接近。
| 表 3 P1点沉降数据的LS、TLS和ULS的预测结果以及相对误差 Tab.3 Forecasted Results and Relative Error of LS, TLS and ULS (P1) |
 |
| 表 4 P2点沉降数据的LS、TLS和ULS的预测结果以及相对误差 Tab.4 Forecasted Results and Relative Error of LS, TLS and ULS (P2) |
 |
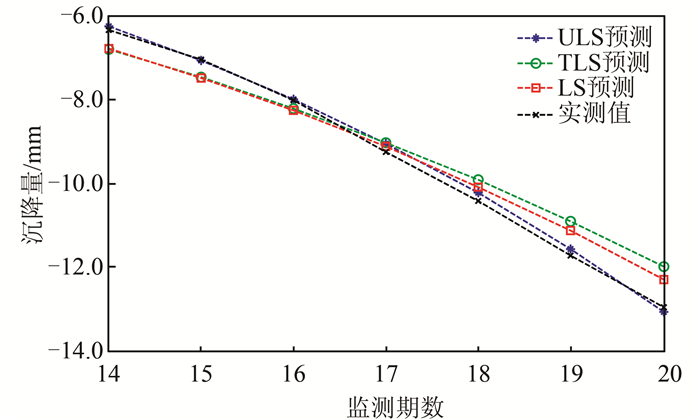 |
| 图 1 P1点的预测和实测曲线 Fig.1 Line of Forecasted Results and Observation Data (P1) |
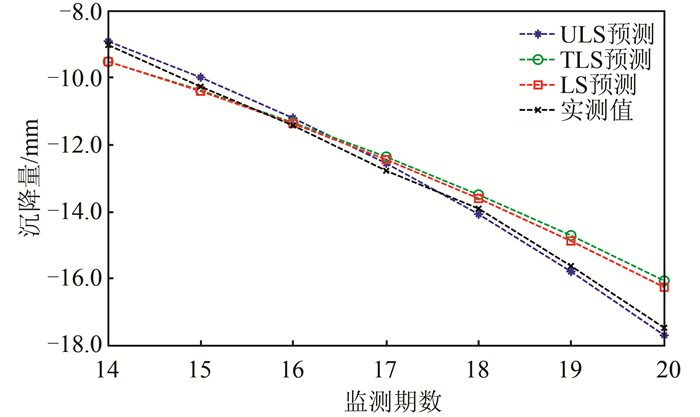 |
| 图 2 P2点的预测和实测曲线 Fig.2 Line of Forecasted Results and Observation Data (P2) |
由式(9)即可求得x(0)的模型理论值
残差:
| $ \varepsilon \left( k \right) = {\mathit{\boldsymbol{x}}^{\left( 0 \right)}}\left( k \right) - {{\mathit{\boldsymbol{\hat x}}}^{\left( 0 \right)}}\left( k \right),k \ge 1 $ | (15) |
残差均值:
| $ \bar \varepsilon = \frac{1}{n}\sum\limits_{k = 1}^n {\varepsilon \left( k \right)} $ | (16) |
原始数据均值:
| $ \bar x = \frac{1}{n}\sum\limits_{k = 1}^n {{\mathit{\boldsymbol{x}}^{\left( 0 \right)}}\left( k \right)} $ | (17) |
残差以及原始数据的方差为:
| $ S_1^2 = \frac{1}{n}\sum\limits_{k = 1}^n {{{\left( {\varepsilon \left( k \right) - \bar \varepsilon } \right)}^2}} $ | (18) |
| $ S_2^2 = \frac{1}{n}\sum\limits_{k = 1}^n {{{\left( {{\mathit{\boldsymbol{x}}^{\left( 0 \right)}}\left( k \right) - \bar x} \right)}^2}} $ | (19) |
计算后验差比值c和小概率p:
| $ c = \frac{{{S_1}}}{{{S_2}}} $ | (20) |
| $ p = p\left\{ {\left| {\varepsilon \left( k \right) - \bar \varepsilon } \right| < 0.674\;5{S_2}} \right\} $ | (21) |
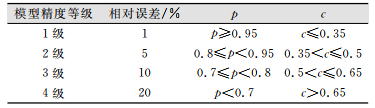
根据计算出的c和p以及相对误差来评定模型的精度,精度等级如表 5所示。
| 表 5 模型精度等级 Tab.5 Model's Accuracy Level |
 |
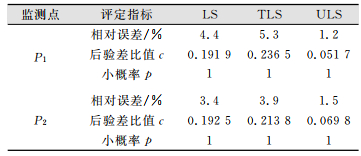
利用监测点P1和P2数据建立沉降GM(1, 1)模型,由3种平差方法计算后的模型精度数据如表 6所示(表格中的相对误差实际上取值为预测7期结果的平均相对误差),从表 6可以看到,在后验差比值和小概率两个指标下,3种平差算法解算GM(1, 1)模型得到的预测结果均为1级,而在相对误差指标的评定中,除了监测点P1在整体最小二乘平差(TLS)下得到的预测结果为3级外,其他情况均为2级。但从各指标的具体数值结果可以看到,带不确定性的平差(ULS)预测结果优于整体最小二乘平差(TLS)和最小二乘平差(LS)。说明了不确定性平差算法在沉降灰色模型中应用的有效性。
| 表 6 监测点P1、P2的模型精度 Tab.6 Model's Accuracy of Points P1 and P2 |
 |
4 结束语
本文提出将不确定度融入GM(1, 1)模型系数矩阵和观测向量,分别加以限制约束,利用min-max准则,结合残差中不确定性的误差传播规律,避免了整体最小二乘平差考虑不确定性但不确定性未知导致的模型修正过度,而参数估计结果不佳的弊端,在一定程度上提高了沉降GM(1, 1)模型预测的精度。从处理某建筑物监测点P1和P2的沉降预测结果来看,带不确定性的平差算法(ULS)的预测结果优于整体最小二乘平差(TLS)和最小二乘平差(LS),说明了不确定性平差算法在沉降灰色模型中应用的有效性。
| [1] |
焦明连, 蒋廷臣. 基于小波分析的灰色预测模型在大坝安全监测中的应用[J]. 大地测量与地球动力学, 2009, 29(2): 115-117. |
| [2] |
贾明娟, 牛冲, 隋冰冰, 等. 基于灰色模型的建筑物沉降预测研究[J]. 测绘与空间地理信息, 2016, 39(1): 44-46. DOI:10.3969/j.issn.1672-5867.2016.01.014 |
| [3] |
明祖涛, 刘军, 夏力, 等. 改进的灰色模型在高铁沉降预测中的应用[J]. 测绘科学, 2015, 40(4): 137-140. |
| [4] |
徐卫东, 伍锡锈, 欧海平. 基于时间序列分析和灰色理论的建筑物沉降预测模型研究[J]. 测绘地理信息, 2012, 37(6): 23-25. |
| [5] |
宋迎春, 谢雪梅, 陈晓林. 不确定性平差模型的平差准则与解算方法[J]. 测绘学报, 2015, 44(2): 135-141. |
| [6] |
宋迎春, 金昊, 崔先强. 带有不确定性的观测数据平差解算方法[J]. 武汉大学学报·信息科学版, 2014, 39(7): 788-792. |
| [7] |
顾勇为, 归庆明. 航空重力测量数据向下延拓基于信噪比的正则化方法的研究[J]. 测绘学报, 2010, 39(5): 458-464. |
| [8] |
谢建, 朱建军. 等式约束病态模型的正则化解及其统计性质[J]. 武汉大学学报·信息科学版, 2013, 38(12): 1440-1444. |
| [9] |
王乐洋, 于冬冬. 病态总体最小二乘问题的虚拟观测解法[J]. 测绘学报, 2014, 43(6): 575-581. |
| [10] |
曾文宪, 方兴, 刘经南, 等. 附有不等式约束的加权整体最小二乘算法[J]. 测绘学报, 2014, 43(10): 1013-1018. |
| [11] |
邹渤, 宋迎春, 唐争气, 等. 沉降观测AR模型的不确定性平差算法[J]. 大地测量与地球动力学, 2016, 36(8): 686-688. |
| [12] |
谢建, 朱建军. 等式约束对病态问题的影响及约束正则化方法[J]. 武汉大学学报·信息科学版, 2015, 40(10): 1344-1348. |
| [13] |
朱建军, 谢建, 陈宇波. 不等式约束对平差结果的影响分析[J]. 测绘学报, 2011, 40(4): 411-415. |
| [14] |
王乐洋, 许才军, 汪建军. 附有病态约束矩阵的等式约束反演问题研究[J]. 测绘学报, 2009, 38(5): 397-401. DOI:10.3321/j.issn:1001-1595.2009.05.004 |
| [15] |
刘斌, 李术才, 李树忱, 等. 基于不等式约束的最小二乘法三维电阻率反演及其算法优化[J]. 地球物理学报, 2012, 55(1): 260-268. DOI:10.6038/j.issn.0001-5733.2012.01.025 |
| [16] |
张松林, 陈德虎. 带不等式约束的间接平差模型的三种解算方法比较[J]. 大地测量与地球动力学, 2013, 33(2): 41-44. |
| [17] |
左廷英, 陈仲儿, 宋迎春. 参数有界约束下的最小二乘平差算法[J]. 测绘工程, 2015(9): 1-4. DOI:10.3969/j.issn.1006-7949.2015.09.001 |
| [18] |
袁维红, 王江荣, 赵睿, 等. 基于卡尔曼滤波算法的动态灰色GM(1, 1)模型在路基沉降分析中的应用[J]. 建筑设计管理, 2016(10): 79-81. DOI:10.3969/j.issn.1673-1093.2016.10.019 |
| [19] |
刘军, 易胜文, 晋涛, 等. 改进的灰色模型在建筑物沉降预测中的应用研究[J]. 城市勘测, 2015(1): 149-151. DOI:10.3969/j.issn.1672-8262.2015.01.043 |
| [20] |
陈仲儿, 左廷英, 宋迎春. 参数有界约束下平差模型的一种新算法[J]. 大地测量与地球动力学, 2015, 35(3): 440-444. |
| [21] |
钱传俊, 舒国栋, 江宝锋. 改进总体最小二乘迭代解法在病态平差模型中的应用[J]. 现代测绘, 2016, 39(4): 1-2. DOI:10.3969/j.issn.1672-4097.2016.04.001 |
| [22] |
袁豹, 岳东杰, 张洋. 基于总体最小二乘的Aa(p)模型及其在建筑物沉降预测中的应用[J]. 勘察科学技术, 2012(6): 42-45. DOI:10.3969/j.issn.1001-3946.2012.06.011 |
| [23] |
张玉堂, 程新文. 灰色模型与智能算法组合模型在变形预测中的应用[J]. 地理空间信息, 2011, 9(2): 109-111. DOI:10.3969/j.issn.1672-4623.2011.02.037 |
 2019, Vol. 44
2019, Vol. 44

