| 基于DWG文件的图件坐标转换方法研究与实现 |
大地基准规定了测绘作业的起算基准,包括空间定位、定向及尺度标准。我国的大地基准自20世纪60年代以来经历了一系列完善、更新的演化过程[1-3]。传统的国家大地坐标系有1954北京坐标系、1980西安坐标系以及地方独立坐标系等。近年来,我国基于空间大地测量技术建立了2000国家大地坐标系[4-7],目前不同坐标系之间转换方法的研究多且较为成熟,随着2000国家大地坐标系的推广,如何将大地坐标转换方法扩展至图件转换中,实现不同坐标系下地形图成果的高精度转换,成为一个亟待解决的问题[8-10]。
我国现有的1:25万、1:5万、1:1万等国家基本比例尺地形图主要为数字线划图,其中在图件存储过程中,多以自动计算机辅助设计(auto computer aided desgin, AutoCAD)软件的DWG或DXF格式存储。DWG是AutoCAD软件的二进制矢量图形编码格式,DXF是文本格式,基于DXF格式进行坐标转换可以较好地脱离AutoCAD软件来独立开发程序,该方法通用性好,且易实现。但由于DWG格式转存DXF过程中,容易出现信息丢失的情况,并且DXF中的图块主要用基点及其边界来描述,基点的选择具有一定的随意性,导致图块坐标转换处理较为复杂[10]。本文研究基于DWG格式的图件坐标转换方法,研制出DWG图件坐标转换软件, 解决了转换中存在的问题。
1 DWG文件及其存储规则 1.1 DWG文件及AutoCAD软件二次开发技术DWG格式文件是二进制的,共有5种数据形式:字符型、字节型、整型(双字节)、长整型(4字节)、双精度浮点数。DWG文件的数据结构由5部分组成,分别是头部、实体部、表部、块实体部和应急头部,其中实体部保存着该图形中的全部实体。图形实体是AutoCAD中的基本图形单元,如点、线、圆、弧、块、尺寸标注等。
ObjectARX是AutoCAD软件的二次开发软件包,提供了面向对象的开发环境及运用程序结构,是一个动态链接库。ObjectARX能共享AutoCAD的地址空间,并可通过多种方式调用AutoCAD软件的命令,同时可以直接访问数据结构和图形系统,在AutoCAD软件编辑环境下的所有动作或行为都可以利用ObjectARX中对应的函数来实现,且具有较高的效率。
1.2 DWG数据库存储组织方式AutoCAD软件中的DWG图形文件,其实质上是存储在图形数据库中对象的集合,包括实体(点、线、面、体、尺寸、文本)和非实体对象(图层、线型、各种视图)等。
在AutoCAD中,表与对应的表记录分别代表数据库中存储的各种实体,最为常用的是块表以及块表记录。块表中存储了所有的块表记录Id,而块表记录中存储了数据库中所有图形实体的ObjectId。需要注意的是,表以及表记录中存储的都是对应实体对象的指针即Id,并非存储实体对象的数据。ObjectARX中提供了内置函数GetObject,可以方便根据ObjectId获取实体对象。ObjectId是Database数据库中实体对象在内存中存储的唯一标识,每次打开DWG文件时,数据库会自动分配并创建ObjectId,这也意味着ObjectId会随着每次打开DWG文件读取数据库发生变化,但它唯一地指向数据库中的同一个实体对象。
ObjectARX广泛应用了类的概念来简化代码结构。每一个类的主要作用在于构建、操作具体的实体对象,每一个类精确代表一个AutoCAD的组件,各组件组成不同的程序集,ObjectARX中定义了图形对象的基类为DbOjbect,其上派生出了实体类,实体类派生出曲线类,曲线类派生出线类,进而组织起数据存储和表达形式。坐标作为实体类的一个属性是有一组能够表达其特征的点的集合。
2 基于DWG文件的图件坐标转换方法 2.1 图形点对点的坐标转换方法AutoCAD用点、线、面的形式表现图件实体,基于DWG文件的图形转换方法思路如下:首先,将复杂实体分解为一系列特征点及参数;而后,对实体的每一个特征点进行坐标转换;最后,利用转换后的点坐标重新恢复实体对象。该方法基于点对点的模式进行图件转换,图件中的每一个实体对象的转换精度取决于点的转换精度。为了保持图件信息转换前后的一致性,转换过程中只需要修改实体对象的坐标值,其余属性保持不变。可先复制待转换文件,然后逐一修改文件中实体对象的坐标,进而简化转换流程。
AutoCAD软件中内置有实体对象仿射变换的功能,ObjectARX中定义了仿射变换函数TransformBy,该函数主要实现实体对象的平移、旋转以及缩放等几何变换。由于ObjectARX中TransformBy函数封装在实体类内,并且以实体为操作对象,因此,图件转换中提取特征点坐标、点对点转换以及还原实体等流程均可由实体对象调用自身的TransformBy函数进行仿射变换来完成。需要解决的问题就是建立TransformBy仿射变换模型与大地测量4参数转换模型的联系,利用坐标转换4参数构建TransformBy函数的输入参数。
2.2 仿射变换模型与大地坐标转换模型分析TransformBy函数使用Matrix3d类的变换矩阵进行实体对象的平移、旋转以及缩放。Matrix3d类中定义了Displacement、Rotation以及Scaling共3个成员函数,分别用于构建平移、旋转以及缩放矩阵。Displacement以平移的三维矢量作为参数,Rotation需指定旋转参考点、旋转角、旋转轴,其中,旋转角在垂直于旋转轴的平面内,并构成右手系,以逆时针方向为正。Scaling函数以缩放基点以及尺度因子为参数。地形图的4参数坐标转换可简化各实体对象以z轴为旋转轴,在x-y轴平面内平移、缩放以及旋转,如图 1所示。
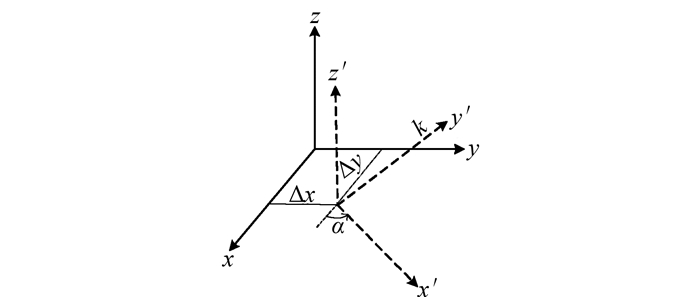 |
| 图 1 AutoCAD软件中仿射变换示意图 Figure 1 Diagram of Affine Transformation in AutoCAD Software |
Matrix3d类作为ObjectARX定义的矩阵类,是一个4×4方阵,以z轴为旋转轴,对应的平移、旋转、缩放方阵Rz可表示为:
| ${{\mathit{\boldsymbol{R}}}_{z}}=\left[ \begin{matrix} k\cos \alpha & \sin \alpha & 0 & 0 \\ -\sin \alpha & k\cos \alpha & 0 & 0 \\ 0 & 0 & k & 0 \\ \Delta x & \Delta y & 0 & 1 \\ \end{matrix} \right]$ | (1) |
仿射变换模型为:
| $\begin{align} & \left[ x'\ \ y'\ \ z'\ \ 1 \right]=\left[ x\ \ y\ \ z\ \ 1 \right]\cdot \\ & \left[ \begin{matrix} k\cos \alpha & \sin \alpha & 0 & 0 \\ -\sin \alpha & k\cos \alpha & 0 & 0 \\ 0 & 0 & k & 0 \\ \Delta x & \Delta y & 0 & 1 \\ \end{matrix} \right] \\ \end{align}$ | (2) |
式(1)、式(2)中,Δx、Δy为平移量;k为缩放因子;α为旋转角;(x,y,z)为待转换坐标;(x′, y′, z′)为转换后坐标。从公式中不难发现,仿射变换模型与大地坐标转换模型相似。因此,通过仿射变换可以实现与大地坐标转换相同的功能。
大地测量中定义的x、y轴与AutoCAD软件的定义刚好相反,仿射变换中平移量(Δx,Δy)应为4参数中的(Δy,Δx);仿射变换模型与4参数转换模型中,旋转角的定义一致,因此,仿射变换中旋转矩阵可以z轴作为旋转轴,以α作为旋转角构建;4参数中定义的缩放因子m与Matrix3d中比例因子k定义不同,两者的转换方法为k=m×10-6+1.0。4参数转换中并不涉及高程,而仿射变换模型中同样对坐标z分量进行了缩放。若实体对象的坐标中含有z分量,则转换后将发生变化。ObjectARX定义的图形类中,线、弧、圆、椭圆、文本标注以及solid等不存在z分量,转换时z值当0处理,对转换无影响。二维多段线、三维多段线、填充块等实体对象具有Elevation属性,变换时,该属性会被默认为z分量,因此,需要上述6类实体进行处理,以防止转换前后其高程值产生变化,具体方法为转换前记录实体对象的Elevation或者z值,转换完成后再重新赋回。
3 图件坐标转换软件实现本文在Visual Studio的开发平台上,使用C#语言研制了基于DWG文件的图形坐标转换软件,软件的主要流程如图 2所示。
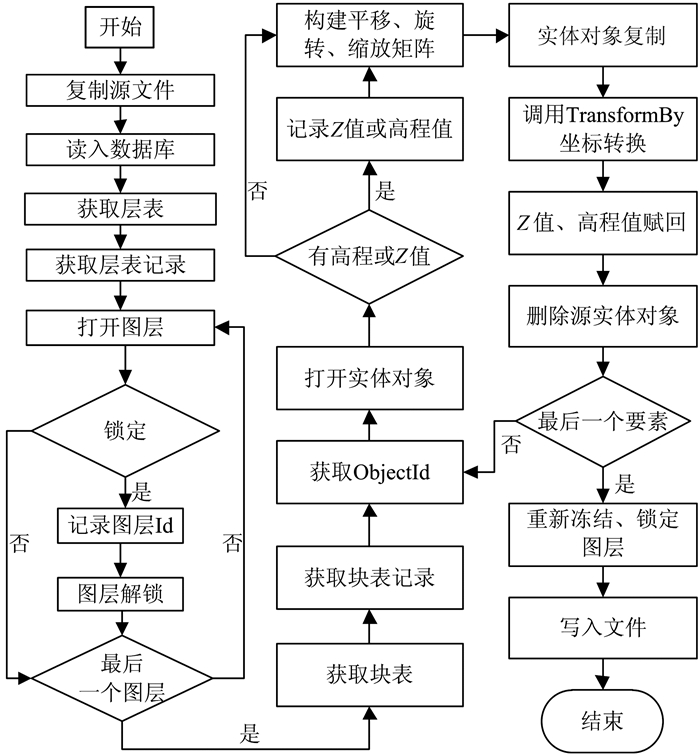 |
| 图 2 图件坐标转换软件流程图 Figure 2 Flow Chart of Map Coordinate Transformation Software |
4 图件转换实例
利用本文研制的软件对试验数据进行了处理,试验数据如图 3所示,图件上包括点、线、填充体、文字、块参考等地形图中的常见实体对象。本文提取了转换后图件中多边形填充实体边界点(图中①)、块参考的标记点(图中②)以及文字的标记点(图中③)等实体对象特征点的坐标,如表 1所示。
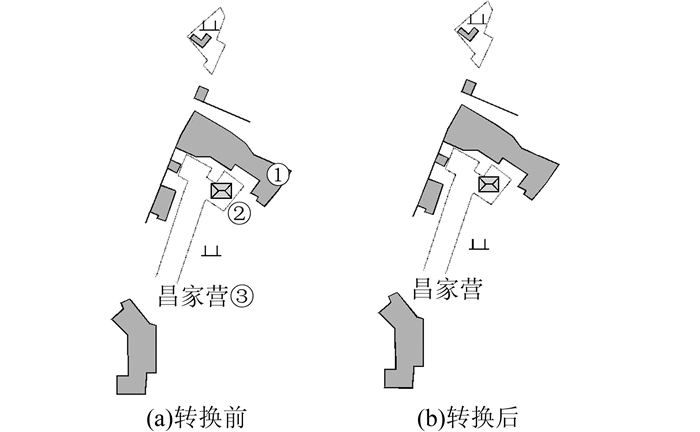 |
| 图 3 图件转换示例 Figure 3 Example of Map Transformation |
| 表 1 图件转换后实体对象的特征点坐标验证/m Table 1 Coordinate Test of Feature Points in Entity Object After Map Transformation/m |
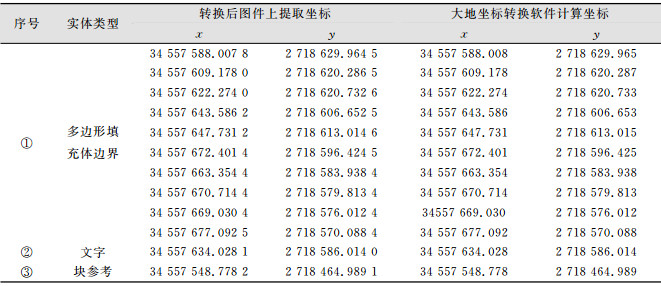 |
现有方法在进行转换时容易出现填充体与外围边界分离的情况,从图 3中可以看出,利用本文所研制的软件进行图形转换后,点、线、面、填充体、文字、块参考等实体对象在转换后其相对关系都未发生改变,尤其是填充体,边界线与填充包裹严密,未出现分离的情况。可见,本文提出的方法较好地保证了图件上各类实体对象的一致性。表 1中列出了转换后图件上提取的填充体多边形边界特征点、文字标记点以及块参考标记点坐标,利用大地控制点转换软件,采用相同的4参数对转换前图件中提取的相同特征点坐标(文本格式)进行转换,上述两种方式获得的特征点坐标之间的差异小于1 mm。可见,利用本文研制的软件进行图形坐标转换,其转换精度取决于大地坐标转换参数的精度,图件转换过程中并不存在额外的精度损失。
5 结束语本文提出了图件点对点的坐标转换方法,建立了仿射变换模型与大地坐标4参数转换模型的联系,基于AutoCAD软件的二次开发技术ObjectARX,研制了地形图坐标转换软件,实现了地形图图件高效、精确、一致的坐标转换。
| [1] |
陈俊勇. 我国建立现代大地基准的思考[J].
世界科技研究与发展,2003,25(3) : 1–4.
Chen Junyong. On the Establishment of Chinese Modern Geodetic Coordinate System[J]. World Sci-Tech R&D,2003,25(3) : 1–4. |
| [2] |
刘经南, 刘晖, 邹蓉, 等. 建立全国CORS更新国家地心动态参考框架的几点思考[J].
武汉大学学报·信息科学版,2009,34(11) : 1262–1265.
Liu Jingnan, Liu Hui, Zou Rong, et al. Some Thoughts on the Establishment of Nationwide Continuously Operating Reference Stations[J]. Geomatics and Information Science of Wuhan University,2009,34(11) : 1262–1265. |
| [3] |
党亚明, 陈俊勇. 全球大地测量地心坐标参考框架最新进展[J].
测绘科学,2004,29(1) : 61–63.
Dang Yaming, Chen Junyong. New Development of Global Geodetic Reference Frame[J]. Science of Surveying and Mapping,2004,29(1) : 61–63. |
| [4] |
陈俊勇. 中国现代大地基准--中国大地坐标系统2000(CGCS 2000)及其框架[J].
测绘学报,2008,37(3) : 269–271.
Chen Junyong. Chinese Modern Geodetic Datum-Chinese Geodetic Coordinate System 2000(CGCS 2000) and Its Frame[J]. Acta Geodaetica et Cartographica Sinica,2008,37(3) : 269–271. |
| [5] |
程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS 80和WGS 84的比较[J].
测绘学报,2009,38(3) : 189–194.
Cheng Pengfei, Wen Hanjiang, Cheng Yingyan, et al. Parameters of the CGCS 2000 Ellipsoid and Comparisons with GRS 80 and WGS 84[J]. Acta Geodaetica et Cartographica Sinica,2009,38(3) : 189–194. |
| [6] |
王敏, 张祖胜, 许明元, 等. 2000国家GPS大地控制网的数据处理和精度评估[J].
地球物理学报,2005,48(4) : 817–823.
Wang Min, Zhang Zusheng, Xu Mingyuan. Data Processing and Accuracy Analysis of National 2000'GPS Geodetic Control Network[J]. Chinese Journal of Geophysics,2005,48(4) : 817–823. |
| [7] |
陈俊勇, 杨元喜, 王敏, 等. 2000国家大地控制网的构建和它的技术进步[J].
测绘学报,2007,36(1) : 1–8.
Chen Junyong, Yang Yuanxi, Wang Min, et al. Establishment of 2000 National Geodeitc Control Network of China and Its Technological Progress[J]. Acta Geodaetica et Cartographica Sinica,2007,36(1) : 1–8. |
| [8] |
姜卫平, 马强, 刘鸿飞. CORS系统中坐标移动转换方法及应用[J].
武汉大学学报·信息科学版,2008,33(8) : 775–778.
Jiang Weiping, Ma Qiang, Liu Hongfei. Coordinate Mobile Transformation in CORS System and Its Application[J]. Geomatics and Information Science of Wuhan University,2008,33(8) : 775–778. |
| [9] |
谢鸣宇, 姚宜斌. 三维空间与二维空间七参数转换参数求解新方法[J].
大地测量与地球动力学,2008,28(2) : 104–109.
Xie Mingyu, Yao Yibin. A New Method for Solution of Seven-Parameter Transformation Between 3D and 2D Spaces[J]. Journal of Geodesy and Geodynamics,2008,28(2) : 104–109. |
| [10] |
姚宜斌, 孔建. 基于DXF文件的图件转换方法研究及程序实现[J].
大地测量学与地球动力学,2011,31(1) : 117–122.
Yao Yibin, Kong Jian. Research on Graphic Conversion Method and Program Implementation Based on DXF File[J]. Journal of Geodesy and Geodynamics,2011,31(1) : 117–122. |
 2016, Vol. 41
2016, Vol. 41

