| 北斗三号实时轨道改正数生成及服务性能分析 |
2. 中国电子科技集团公司第二十研究所,陕西 西安,710068
2. The 20th Research Institute of China Electronics Technology Group Corporation, Xi' an 710068, China
北斗卫星导航系统(BeiDou navigation satellite system,BDS)全球星座由24颗中圆地球轨道(medium earth orbit, MEO)、3颗地球静止轨道(geostationary earth orbit, GEO)和3颗倾斜地球同步轨道(inclined geosynchronous satellite orbit, IGSO)3种类型卫星组成。2018-12-27,中国卫星导航系统管理办公室对外宣布北斗三号(BDS-3)基本系统建设完成并开始提供全球服务,并计划于2020年全面完成全球组网[1]。截至2020年3月底,BDS-3已有29颗卫星发射入轨,最后1颗BDS-3 GEO卫星计划将于2020-05发射。卫星轨道是导航系统服务的基础,随着用户对实时定位要求的提高,实时轨道已逐渐成为导航系统应用的关键。
传统的实时轨道一般从各导航系统对外播发的广播星历或国际GNSS服务组织(International Global Navigation Satellite System Service, IGS)及其分析中心提供的超快速轨道两种途径获得。然而,广播星历精度较差,IGS超快速星历(IGS ultra-rapid ephemeris,IGU)等超快速轨道无法实时收发。为满足实时精密单点定位的需求,自2007年开始,IGS启动IGS实时试点项目(IGS real-time pilot project, IGS-RTPP),由各机构通过互联网进行RTCM网络传输的协议(networked transport of RTCM via internet protocol, NTRIP)以状态空间表示(state space representation, SSR)的形式向全球用户播发实时改正数[2-3],SSR信息更适合于GNSS单点定位的误差改正[3]。目前,针对BDS-3实时轨道已有大量研究。王海春等[4]研究表明,BDS-3广播星历轨道径向精度优于0.1 m,三维精度优于1 m,较BDS-2有较大提升;Yan等[5]采用72 h弧段的BDS-3 MEO卫星定轨试验表明,BDS-3 MEO卫星轨道24 h重叠弧段1D RMS精度优于5 cm;Zhang等[6]的BDS-3卫星定轨试验表明,重叠弧段精度可达到同样的精度水平;戴金倩等[7]研究表明,BDS-3实时径向轨道误差优于10 cm;Zhang等[8]对IGS不同分析中心的GPS实时轨道精度进行了统计分析,研究结果显示,GPS轨道均方根误差(root mean square error, RMSE)处于3.8~7. 5 cm范围;Kazmierski等[9]评价了法国国家太空研究中心(Centre National d’Etudes Spatiales, CNES)的全球定位系统(global positioning system,GPS)、全球卫星导航系统(global navigation satellite system,GLONASS)、伽利略定位系统(Galileo positioning system, Galileo)、BeiDou MEO和BeiDou IGSO的实时轨道产品精度;Wang等[10]研究表明,截止2018年,常用的实时产品中仅有CNES可提供4系统实时产品。目前,已有包括CNES在内的部分机构播发的实时产品中包含BDS-3实时轨道改正数。但是,上述研究均未对BDS-3卫星实时轨道改正数计算和服务性能进行系统的研究和分析。
首先, 本文利用简化动力学定轨法和滑动窗口法[11]设计了BDS-3实时精密定轨策略,进行了连续一个月的BDS-3卫星实时精密轨道解算; 然后, 提出了BDS-3实时轨道改正数生成和恢复算法,计算了30 s更新频率的BDS-3实时轨道SSR信息,并对每幅SSR信息在一个有效期内的精度损失进行了统计分析; 最后,研究讨论了SSR信息的有效服务时长,分析了轨道改正数的服务性能,进一步为实时服务应用提供支撑。
1 实时精密定轨策略构建精确的卫星力学模型是导航卫星精密定轨的关键。本文采用简化动力学定轨法,合理平衡动力学信息和几何观测信息[11]。BDS-3卫星实时精密定轨涉及的关键力模型和解算策略如表 1所示。表 1中缩写代表含义为系统间偏差(inter-system bias,ISB)、天顶对流层延迟(zenith troposphere delay,ZTD)。
| 表 1 关键力模型及数据处理策略 Tab.1 Strategies for Data Processing and Key Force Model |
 |
2 轨道改正数解算
轨道改正数实质为实时精密轨道对广播星历的修正。本文设计的轨道改正数播发频率为30 s,而精密轨道产品的采样间隔为300 s,所以在解算改正数之前,首先,采用拉格朗日9阶插值算法对精密轨道进行插值,求得各基准时刻的卫星位置和速度;然后,对精密轨道做天线相位中心偏差(antenna phase center offsets,PCO)改正,将其从相对于卫星质心的坐标转换为相对于相位中心的坐标;将基准时刻卫星位置和速度与广播星历计算的卫星位置和速度作差后,可得地固系下轨道改正数;最后,经过坐标转换将地固系下的轨道改正数转换到卫星坐标系下,即在卫星轨道切向、法向和径向下的轨道改正数。
1) 精密轨道进行PCO改正为:
| $ \mathit{\boldsymbol{X}}{_{{\rm{orb}}}} = \mathit{\boldsymbol{A}}{\rm{ }} \times {\rm{ }}{\mathit{\boldsymbol{X}}_{{\rm{pco}}}} + {\rm{ }}{\mathit{\boldsymbol{X}}_{{\rm{com}}}} $ | (1) |
式中,Xcom为相对于卫星质心的三维位置;Xpco为卫星的PCO改正信息;A表示旋转矩阵;Xorb表示相对于卫星相位中心的三维位置。
2) 与基准时刻广播星历计算所得卫星位置和速度作差为:
| $ {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{X}}{\rm{ }} = {\rm{ }}{\mathit{\boldsymbol{X}}_{{\rm{nav}}}} - {\rm{ }}{\mathit{\boldsymbol{X}}_{{\rm{orb}}}} $ | (2) |
| $ {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{V}}{\rm{ }} = {\rm{ }}{\mathit{\boldsymbol{V}}_{{\rm{nav}}}} - {\rm{ }}{\mathit{\boldsymbol{V}}_{{\rm{orb}}}} $ | (3) |
式中,δX为卫星位置改正数;Xnav为广播星历计算所得卫星位置;Xorb为精密轨道中卫星位置;δV为卫星速度改正数;Vnav表示广播星历计算所得卫星速度;Vorb表示精密轨道中卫星速度。
3) 坐标转换。根据广播星历计算所得的卫星位置和速度,得出旋转矩阵为:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\boldsymbol{R}}{\rm{ = [ }}\mathit{\boldsymbol{e}}{{\rm{}}_{{R}}}\;\;\mathit{\boldsymbol{e}}{{\rm{}}_{{A}}}\;\;\mathit{\boldsymbol{e}}{{\rm{}}_{{C}}}{\rm{] = }}\\ {\rm{[ }}\frac{{{\mathit{\boldsymbol{V}}_{{\rm{nav}}}}}}{{\left| {{\mathit{\boldsymbol{V}}_{{\rm{nav}}}}} \right|}}{\rm{ \times }}\frac{{{\mathit{\boldsymbol{X}}_{{\rm{nav}}}} \times {\mathit{\boldsymbol{V}}_{{\rm{nav}}}}}}{{\left| {{\mathit{\boldsymbol{X}}_{{\rm{nav}}}} \times {\mathit{\boldsymbol{V}}_{{\rm{nav}}}}} \right|}}\;\frac{{{\mathit{\boldsymbol{V}}_{{\rm{nav}}}}}}{{\left| {{\mathit{\boldsymbol{V}}_{{\rm{nav}}}}} \right|}}\;\frac{{{\mathit{\boldsymbol{X}}_{{\rm{nav}}}} \times {\mathit{\boldsymbol{V}}_{{\rm{nav}}}}}}{{\left| {{\mathit{\boldsymbol{X}}_{{\rm{nav}}}} \times {\mathit{\boldsymbol{V}}_{{\rm{nav}}}}} \right|}}{\rm{]}} \end{array} $ | (4) |
由此可得星固系下坐标改正数为:
| $ {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{X}}{{\rm{}}_{{S}}}{\rm{ = }}\mathit{\boldsymbol{R}}{{\rm{}}^{{\rm{ - 1}}}}{\rm{ \times \mathsf{ δ} }}\mathit{\boldsymbol{X}} $ | (5) |
| $ {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{V}}{{\rm{}}_{{S}}}{\rm{ = }}\mathit{\boldsymbol{ }}\mathit{\boldsymbol{R}}{{\rm{}}^{{\rm{ - 1}}}}{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{V}} $ | (6) |
式中,R为旋转矩阵;eR、eA、eC分别表示径向、切向、法向单位向量;δXS为星固系下基准时刻的位置改正数;δVS为星固系下基准时刻的速度改正数。
卫星实时轨道改正数计算主要包括实时轨道解算、轨道插值和轨道改正数解算,具体计算流程如图 1所示。
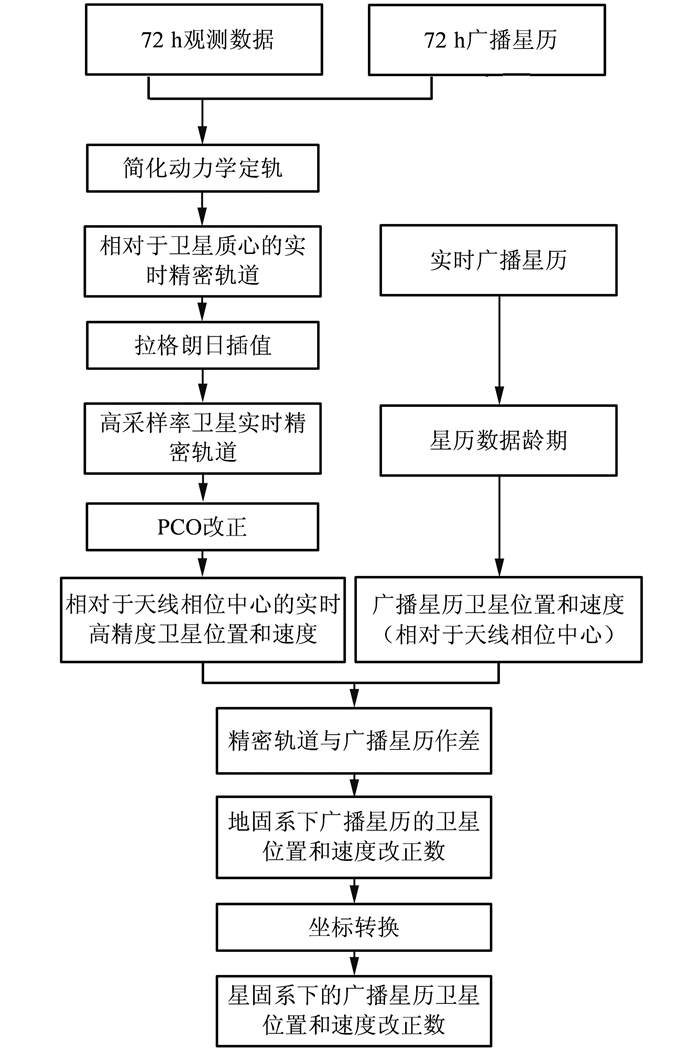 |
| 图 1 卫星实时轨道改正数计算流程 Fig.1 Flow Chart of Real-Time Orbit Correction Parameters |
3 根据轨道改正数信息恢复精密轨道
SSR信息中的星历数据期号(issue of data ephemeris, IODE)记录了解算轨道改正数时使用的广播星历参数,当用户使用SSR信息时,首先根据该参数寻找相应的广播星历参数,然后计算改正后的卫星位置。
1) 计算观测时刻SSR位置改正信息为:
| $ {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{X}}{\rm{ }}\left( t \right) = {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{X}}_{{S}}} + {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{V}}_{{S}}} \times \left( {t - {t_0}} \right) $ | (7) |
2) 坐标转换,计算观测时刻地固系下卫星位置改正信息为:
| $ {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{X}}_{{\rm{orb}}}}\left( t \right) = {\rm{ }}\mathit{\boldsymbol{R}}{\rm{ }} \times {\rm{ \mathsf{ δ} }} \mathit{\boldsymbol{X}}{\rm{ }}\left( t \right) $ | (8) |
3) 计算经轨道改正数改正后观测时刻的卫星位置为:
| $ {\mathit{\boldsymbol{X}}_{{\rm{orb}}}}\left( t \right) = {\rm{ }}{\mathit{\boldsymbol{X}}_{{\rm{nav}}}}\left( t \right) - {\rm{ \mathsf{ δ} }}{\mathit{\boldsymbol{X}}_{{\rm{orb}}}}(t) $ | (9) |
式中,观测时刻为t;SSR信息基准时刻为t0;δXS为星固系下基准时刻的卫星位置改正数;δVS为星固系下基准时刻的卫星速度改正数;δX (t)为星固系下t时刻的卫星位置改正数;R为旋转矩阵;δXorb(t)表示地固系下t时刻的卫星位置改正数;Xnav(t)表示由广播星历计算所得t时刻的卫星位置;Xorb(t)为经轨道改正数改正后t时刻卫星相位中心位置。
4 实时精密轨道精度分析数据处理时段选择2019年年积日306至335天,由于多模GNSS实验网络(Multi-GNSS experiment,MGEX)测站接收机升级,该时段已有较多测站可接收BDS-3信号。考虑到BDS-3仍处于建设中,虽然测站增多但仍不能完全满足高精度定轨需求,因此,选择72 h定轨弧长解算高精度实测轨道,并通过拟合外推计算预报轨道,综合考虑解算耗时与预报轨道精度衰减情况,选取预报部分3~6 h弧段作为实时轨道,更新间隔为3 h。实时轨道更新处轨道跳变为cm级或dm级,使用该轨道修正精度为m级的广播星历时,此跳变可忽略不计。
选取全球分布较为均匀的91个MGEX定轨跟踪站进行GPS/BDS-3联合定轨,GPS数据频点为L1/L2,BDS-3数据频点为B1I/B3I。所选91个定轨跟踪站均可提供BDS-3B1I/B3I频点双频观测数据,但BDS-3系统中C32~C37卫星观测数据比C19~C30卫星略少。在全部91个定轨跟踪站中,有50个跟踪站可以提供小时文件观测数据,由于文件时延较短,实时解算时包含小时文件的跟踪站数据基本可以覆盖全部72 h解算弧段,而天文件因为存在1天的延迟,因此只能覆盖部分弧段。定轨跟踪站分布如图 2所示。
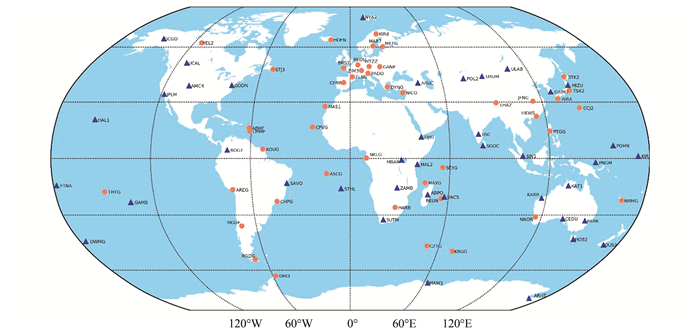 |
| 图 2 精密定轨测站分布图 Fig.2 Sites Distribution of Precise Orbit Determination |
图 2中,三角形表示可提供小时文件观测数据的定轨跟踪站,圆点代表的测站仅能提供天文件观测数据。
以武汉大学IGS分析中心发布的最终轨道产品为基准,评估本文解算的实时精密轨道实测部分最后24 h弧段和实时轨道精度。实测部分轨道1D RMS如图 3(a)所示,实时轨道1D RMS如图 3(b)所示。
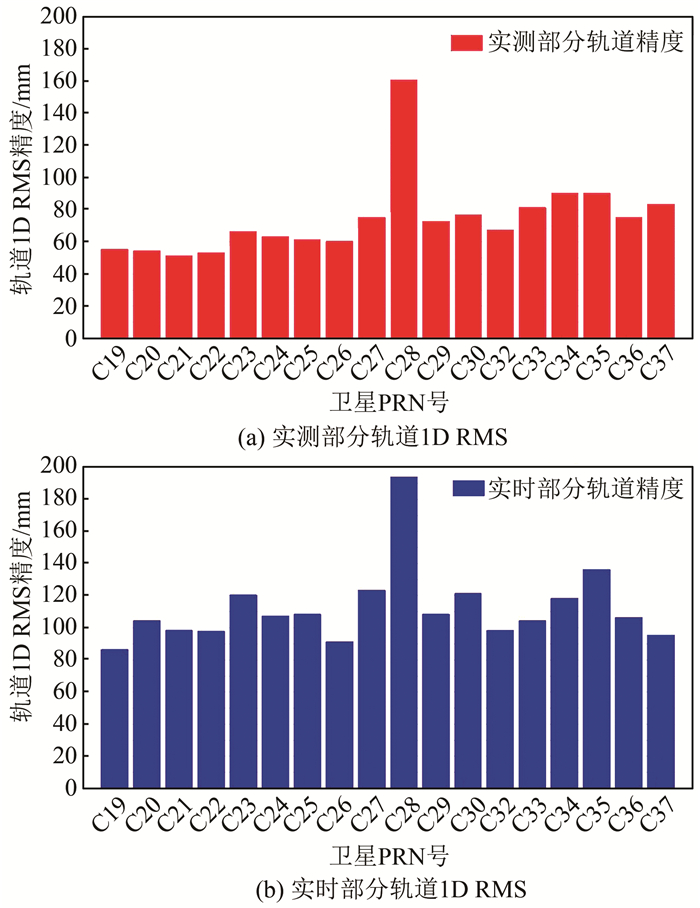 |
| 图 3 实测和实时部分轨道1D RMS Fig.3 Orbit 1D RMS Precision of Measured and Real-Time Section |
根据图 3统计信息可知,BDS-3实时精密轨道实测部分轨道1D RMS平均值为74.1 mm,除C28卫星外,所有卫星1D RMS均优于100 mm。关于C28卫星轨道精度偏低的情况需进一步分析。由于观测数据较少,C33~C37轨道精度稍差,但与C19~C32为同一量级。实时部分轨道1D RMS平均值为111.9 mm,除C28卫星外所有卫星1D RMS均优于140 mm。
5 轨道改正数性能分析获取SSR信息中的IODE参数的方式。对于GPS和Galileo,可直接通过广播星历获取IODE参数,但在BDS广播星历中IODE参数不可用,因此,本文在解算BDS-3轨道改正数时选取了广播星历中包含的周内秒(toe)参数解算IODE参数,算法如下:
| $ {I_{{\rm{IODE}}}} = {\rm{int}}({I_{{\rm{toe}}}} - {\rm{floor}}(\frac{{{I_{{\rm{toe}}}}}}{{86\;400}}) \times 86\;400)/450 $ | (10) |
式中,IIODE为IODE参数值;Itoe为toe参数值;int()为取整函数;floor()为向下取整函数,该算法实质上相当于将广播星历参考时刻的天内秒除以450作为BDS-3的IODE值发布。
当用户使用SSR信息时,可根据IODE信息匹配相应的广播星历,GPS/Galiloe系统可直接匹配,BDS-3可根据上述算法进行匹配。若用户匹配到正确的IODE,使用接收到的SSR中轨道改正信息对该广播星历按照第§3节描述的算法进行改正,便可获得精密卫星位置信息。因轨道改正信息解算时使用预报轨道解算,并综合考虑播发时延和解算耗时等情况,为保证用户能及时接收到基准时刻的改正信息,国际海运事业无线电技术委员会(Radio Technical Commission for Maritime Services,RTCM)规定,轨道改正的基准时刻为播发时刻加上更新频率的一半。本文设计轨道改正数更新频率为30 s,假设基准时刻为t0,则每幅SSR信息的有效期为(t0-15 s)~(t0+15 s)。为评估轨道改正数性能,设计2组方案。
方案1 使用改正信息恢复(t0-15 s)时刻卫星位置,以原实时精密轨道为基准评估精度损失情况。
方案2 使用改正信息恢复(t0+15 s)时刻卫星位置,以原实时精密轨道为基准评估精度损失情况。
方案1和2的轨道精度损失为一个有效期内损失最大值,统计结果如图 4所示。
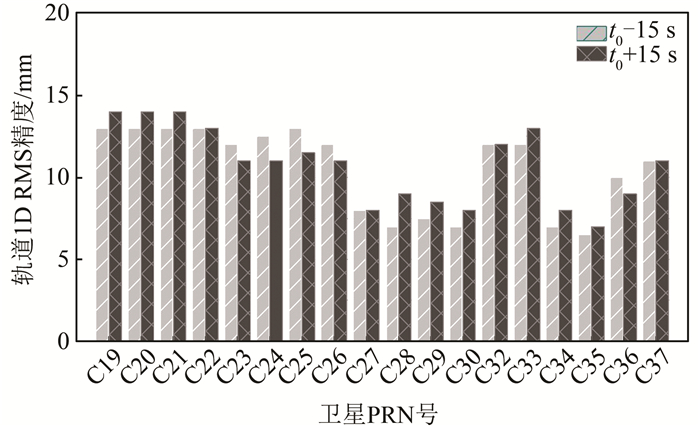 |
| 图 4 有效期内轨道精度损失最大值 Fig.4 Max Orbit Precision Decrease Within the Validity Period |
由图 4可知,(t0-15 s)与(t0+15 s)处恢复所得卫星位置1D RMS平均值分别为10.6 mm与10.7 mm,该精度损失由速度改正数导致。同一卫星在t0±15 s处精度损失基本一致,可推断同一卫星速度改正数精度较为稳定。
在系统运行或用户使用过程中,可能出现由于网络异常等情况导致的改正数未能及时播发或接收,此时,用户将继续使用上一组改正数。因此,设计两组试验检验超出一幅SSR数据龄期后该幅SSR参数的性能。
方案3 使用改正信息恢复t0+30 s时刻卫星位置,以原实时精密轨道为基准评估精度损失情况。
方案4 使用改正信息恢复t0+45 s时刻卫星位置,以原实时精密轨道为基准评估精度损失情况。图 5统计了方案3和方案4恢复所得卫星位置的精度损失。
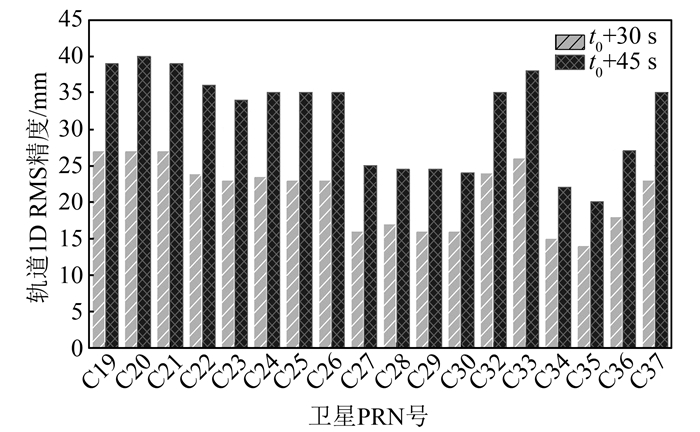 |
| 图 5 方案3和4实时轨道精度损失 Fig.5 Real-Time Orbit Precision Decrease in Scheme 3 and Scheme 4 |
由图 5可得,(t0+30 s)与(t0+45 s)处恢复所得卫星位置精度损失1D RMS平均值分别为21.3 mm与31.6 mm,该精度损失仍由速度改正数导致。当SSR缺失1个历元时,精度损失仍然较小,可继续使用其对广播星历进行改正。
为检验一组SSR参数最大有效时长,进一步设计试验对SSR缺失更多历元的情况进行分析。
方案5 使用改正信息恢复(t0+dt, dt=15+n×30)时刻卫星位置,以原实时精密轨道为基准评估精度损失情况。即评估缺失n组SSR信息时,当前SSR参数的最大精度损失。统计缺失0~25个历元(即(t0+15 s)~(t0+765 s))时恢复所得卫星位置的精度损失。各卫星平均位置精度损失如图 6所示。
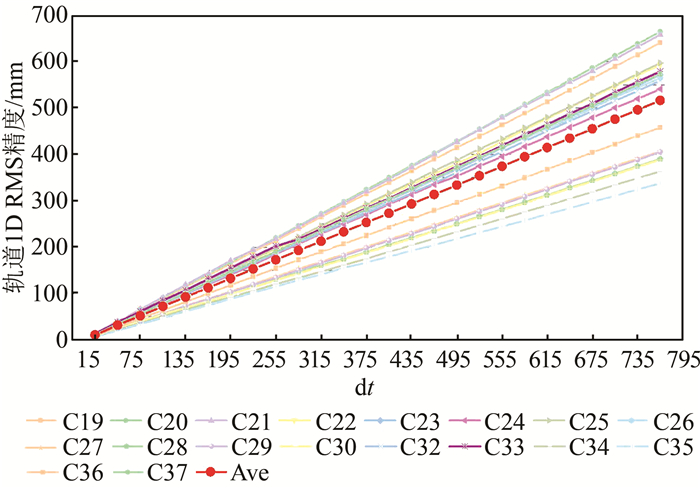 |
| 图 6 各卫星实时轨道精度损失 Fig.6 Real-Time Orbit Precision Decrease for Each Satellite |
由图 6可得,各卫星位置精度损失与SSR信息缺失时间呈线性正相关,分析原因为各卫星速度改正数在短期内保持稳定。当SSR信息持续缺失25个历元,即有效期为12.5 min后,卫星位置平均精度损失超过0.5 m。考虑到BDS-3广播星历精度为m级,此时SSR信息已不具备改正广播星历以提高卫星位置精度的能力。
6 结束语本文首先进行了BDS-3卫星实时精密定轨及精度评定,然后基于计算的实时轨道生成了SSR信息,并对其进行了精度损失和有效服务时长的研究和讨论。结果表明:
1) BDS-3 MEO卫星实时轨道平均精度约为112 mm,且各卫星精度基本一致。BDS-3 GEO和IGSO卫星的观测数据量较少,目前不具备实时定轨和服务条件。
2) 以30 s为更新频率的SSR改正信息中,每幅SSR信息数据龄期内轨道精度损失最大值(t0±15 s处)平均约为11 mm,完全满足实时精密单点定位需求。
3) 各卫星位置精度损失与SSR信息缺失时间呈线性正相关,SSR信息缺失1个历元时,轨道精度损失最大值(t0+45 s处)平均约为32 mm,SSR信息缺失25个历元时,轨道精度损失最大值(t0+765 s处)平均超过0.5 m。因此,建议SSR轨道改正数最长有效服务时长为12.5 min。
| [1] |
Yang Yuanxi, Xu Yangyin, Li Jinlong, et al. Progress and Performance Evaluation of BeiDou Global Navigation Satellite System:Data Analysis Based on BDS-3 Demonstration System[J]. Science China Earth Scien-ces, 2018, 61(5): 614-624. |
| [2] |
夏凤雨, 叶世榕, 赵乐文, 等. 基于SSR改正的实时精密单点定位精度分析[J]. 导航定位与授时, 2017, 4(3): 52-57. |
| [3] |
刘志强, 王解先. 广播星历SSR改正的实时精密单点定位及精度分析[J]. 测绘科学, 2014, 39(1): 15-19. |
| [4] |
王海春, 贾小林, 李鼎, 等. 北斗三号卫星广播星历精度评估分析[J]. 导航定位学报, 2019, 7(4): 60-63. |
| [5] |
Yan Xingyuan, Huang Guanwen, Zhang Qin, et al. Estimation of the Antenna Phase Center Correction Mo-del for the BeiDou-3 MEO Satellites[J]. Remote Sen-sing, 2019, 11(23). DOI:10.3390/rs11232850 |
| [6] |
Zhang Bo, Jia Xiaolin, Sun Fuping, et al. Perfor-mance of BeiDou-3 Satellites: Signal Quality Analysis and Precise Orbit Determination[J]. Advances in Space Research, 2019, 64(3): 687-695. |
| [7] |
戴金倩, 吴迪, 戴小蕾, 等. BDS-3实时精密单点定位精度分析[J]. 测绘通报, 2020(1): 30-34. |
| [8] |
Zhang Liang, Yang Hongzhou, Gao Yang, et al. Evaluation and Analysis of Real-Time Precise Orbits and Clocks Products from DifferentI GS Analysis Centers[J]. Advances in Space Research, 2018, 61(12): 2 942-2 954. |
| [9] |
Kazmierski K, Sosnica K, Hadas T, et al. Quality Assessment of Multi-GNSS Orbits and Clocks for Real-Time Precise Point Positioning[J]. GPS Solutions, 2018, 22(1). DOI:10.1007/s10291-017-0678-6 |
| [10] |
Wang Zhiyu, Li Zishen, Wang Liang, et al. Assessment of Multiple GNSS Real-Time SSR Products from Different Analysis Centers[J]. ISPRS International Journal of Geo-Information, 2018, 7(3). DOI:10.3390/ijgi7030085 |
| [11] |
王乐.BDS卫星实时精密定轨及低轨卫星增强技术研究[D].西安: 长安大学, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10710-1018791476.htm
|
| [12] |
燕兴元, 王乐, 黄观文, 等. BeiDou-3试验卫星精密定轨及钟差精度分析[J]. 测绘科学技术学报, 2018, 35(1): 27-31. |
| [13] |
宁津生, 王正涛. 地球重力场研究现状与进展[J]. 测绘地理信息, 2013, 38(1): 1-7. |
| [14] |
Saastamoinen J. Contributions to the Theory of Atmospheric Refraction[J]. Bulletin Géodésique, 1972, 105(1): 279-298. |
| [15] |
Boehm J, Heinkelmann R, Schuh H, et al. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683. |
| [16] |
Ge M, Gendt G, Dick G, et al. Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions[J]. Journal of Geodesy, 2005, 79(1): 103-110. |
| [17] |
Wang Jin, Huang Guanwen, Yang Yuanxi, et al. FCB Estimation with Three Different PPP Models:Equivalence Analysis and Experiment Tests[J]. GPS Solutions, 2019, 23(4): 1-14. |
 2020, Vol. 45
2020, Vol. 45


