| 基于Cesium的BIM与实景三维模型集成可视化研究 |
2. 中铁第五勘察设计院集团有限公司,北京,102600
2. China Railway Fifth Survey And Design Institute Group Co., Ltd., Beijing 102600, China
建筑信息模型(building information model,BIM)概念起源于20世纪70年代,是对建筑的物理和功能特性的数字化表达,贯穿于建筑从概念、设计、施工、运营维护及拆除的整个生命周期中,提供信息支撑和决策依据。随着信息技术的高速发展,BIM成为了规划设计领域的研究热点,在水立方、上海中心大厦等大型项目中得到广泛应用[1, 2]。
在建筑设计、施工等各个环节都离不开周边环境信息做支撑,GIS作为地理信息的数字化表达载体,正为BIM提供了更大尺度的信息支持。GIS的各类空间分析功能可以为BIM提供决策参考,真正将建筑与环境融为一体[3-6]。吴志强等[7]进一步提出了城市信息模型(city information modeling,CIM)的概念,即CIM=BIM + GIS + 物联网(internet of things,IoT),将微观的BIM、宏观的GIS与IoT数据进行集成统一,形成综合数据处理计算平台,为智慧城市建设提供了技术支撑。
因此,BIM与GIS的组合越来越多的受到国内外学术界和工程界的广泛关注。文献[8-13]分别从语义关联、数据融合、集成方式和工程应用等方面对BIM与GIS的融合展开了探讨。实景三维模型是借助倾斜摄影测量技术获取的地表三维模型,通过多视角航空摄影、空三加密、密集匹配、纹理映射等环节自动计算生成,可真实反映地物地貌特征、数据精度高、自动化程度高,是目前主流的三维GIS数据源之一[4]。Cesium是一款开源的Web端三维GIS开发包,基于WebGL技术和3D-Tiles数据标准实现海量二三维空间数据的跨平台绘制展示。
本文以某磁浮铁路项目为例,介绍BIM与GIS数据集成可视化的实现思路及基于Cesium的实现方法;进一步地介绍BIM与实景三维模型的动态卷帘功能实现思路及效果。
1 集成可视化实现思路BIM与倾斜摄影模型的集成可视化流程如图 1所示。
 |
| 图 1 BIM与倾斜摄影模型集成可视化流程 Fig.1 Integrated Visualization Process of BIM and Oblique Photography Model |
由于各大机构和软件厂商分别定义了各自的数据标准,不同数据标准对应了不同的数据文件格式、要素组织方法及空间索引结构:BIM标准包括RVT、DGN、IFC标准等;实景三维模型标准包括OSGB、SLPK、S3M标准等。与此同时,需分别对BIM模型和实景三维模型进行分层、分块处理,以保证Web端加载性能。3D-Tiles结构是Cesium原生支持的数据标准,渲染时可根据视锥体范围和瓦片索引进行动态调度。因此,加载前需将BIM与实景三维模型分别转换为Cesium支持的3D-Tiles数据标准[14-15]。
实景三维模型由于引入了影像外方位元素、地面控制点,具有绝对坐标基准;而BIM主要用于建筑尺度的信息管理,未引入绝对位置参考,坐标往往采用局部坐标系表达。模型叠加可通过手工配准的方式实现,而顾及到GIS空间计算、分析的精度和准确性需要对BIM模型的位置、姿态及高程进行严密计算,故需通过坐标转换的方式将BIM与实景三维模型的坐标基准进行统一。
BIM模型表现的是建筑设计方案,实景三维模型还原了影像采集时刻的地形地貌特征而未考虑到建筑施工所带来的地形变化。直接将模型根据坐标进行叠加势必会出现重叠和遮挡,两者无法完美套合。因此需考虑到建筑施工所造成的地形变化,对模型衔接区域进行处理。
综上所述,通过数据标准统一、坐标基准统一和模型衔接处理,即可将BIM与实景三维模型进行集成展示。本文重点介绍坐标基准统一方式、模型衔接处理的实现思路,而数据标准统一可通过FME软件及开源程序实现,在此不做赘述。
2 模型坐标基准统一坐标基准统一需通过对BIM的局部坐标根据坐标原点所在绝对坐标及坐标轴指向进行坐标转换计算,转换至地球中心坐标系(earth-centered earth-fixed,ECEF),流程如图 2所示。
 |
| 图 2 BIM坐标转换流程 Fig.2 BIM Coordinate Conversion Process |
首先将局部坐标系旋转至ENU(east-north-Up)坐标系(其中x轴指向南方向,y轴指向东方向,z轴指向天顶方向),再建立ENU坐标系到地球椭球ECEF坐标系之间的转换关系,最后将ENU坐标进行旋转和平移,得到ECEF世界坐标[16]。
1)局部坐标系旋转到ENU坐标系。BIM在局部坐标系下的坐标(x0,y0,z0) 到ENU坐标(x,y,z),需依次绕三轴旋转εz、εy、εx角度,对应的旋转矩阵R(εx,εy,εz)为:
| $ \begin{array}{l} \mathit{\boldsymbol{R}}\left( {{\varepsilon _x}, {\varepsilon _y}, {\varepsilon _z}} \right) = \mathit{\boldsymbol{R}}\left( {{\varepsilon _z}} \right) \cdot \mathit{\boldsymbol{R}}\left( {{\varepsilon _y}} \right) \cdot \mathit{\boldsymbol{R}}\left( {{\varepsilon _x}} \right) = \\ \left( {\begin{array}{*{20}{c}} {\cos {\varepsilon _y}\cos {\varepsilon _z}}&{\sin {\varepsilon _x}\sin {\varepsilon _y}\cos {\varepsilon _z}}&{ - \cos {\varepsilon _x}\sin {\varepsilon _y}\cos {\varepsilon _z} + \sin {\varepsilon _x}\sin {\varepsilon _z}}\\ { - \cos {\varepsilon _y}\sin {\varepsilon _z}}&{ - \sin {\varepsilon _x}\sin {\varepsilon _y}\sin {\varepsilon _z} + \cos {\varepsilon _x}\cos {\varepsilon _z}}&{\cos {\varepsilon _x}\sin {\varepsilon _y}\cos {\varepsilon _z} + \sin {\varepsilon _x}{{\cos }_z}}\\ {\sin {\varepsilon _y}}&{ - \sin {\varepsilon _x}\cos {\varepsilon _y}}&{\cos {\varepsilon _x}\cos {\varepsilon _y}} \end{array}} \right) \end{array} $ | (1) |
2)计算ENU到ECEF坐标系的平移量(X0,Y0,Z0) 及旋转矩阵R (B0,L0,0) 分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{X_\mathit{0}} = \left( {{N_\mathit{0}} + {H_\mathit{0}}} \right)\cos {B_\mathit{0}} \times \cos {L_\mathit{0}}}\\ {{Y_\mathit{0}} = \left( {{N_\mathit{0}} + {H_\mathit{0}}} \right)\cos {B_\mathit{0}} \times \sin {L_\mathit{0}}}\\ {{Z_\mathit{0}} = \left[ {{N_\mathit{0}}\left( {1 - {e^2}} \right) + {H_\mathit{0}}} \right] \times \sin {B_\mathit{0}}} \end{array}} \right. $ | (2) |
| $ {N_\mathit{0}} = \frac{a}{{\sqrt {1 - {e^2}{{\sin }^2}{B_\mathit{0}}} }} $ | (3) |
| $ \begin{array}{l} \mathit{\boldsymbol{R}}\left( {{B_0}, {L_0}, 0} \right) = \mathit{\boldsymbol{R}}\left( {{B_0}} \right)\mathit{\boldsymbol{R}}\left( {{L_0}} \right) = \\ \left( {\begin{array}{*{20}{c}} {\cos {B_0}\cos {L_0}}&0&{ - \sin {B_0}\cos {L_0}}\\ { - \cos {B_0}\sin {L_0}}&{\cos {L_0}}&{\sin {B_0}\sin {L_0}}\\ {\sin {B_0}}&0&{\cos {B_0}} \end{array}} \right) \end{array} $ | (4) |
式中,BIM模型的坐标系原点位于椭球面上的大地坐标为(B0,L0);N0表示卯酉圈半径;a为椭球的长半轴;e为椭球第一偏心率。
3)最终转换关系式为:
| $ \left( {\begin{array}{*{20}{l}} X\\ Y\\ Z \end{array}} \right) = \left( {\begin{array}{*{20}{l}} {{X_\mathit{0}}}\\ {{Y_\mathit{0}}}\\ {{Z_\mathit{0}}} \end{array}} \right) + \mathit{\boldsymbol{R}}\left( {{B_\mathit{0}}, {L_\mathit{0}}, 0} \right) \times \mathit{\boldsymbol{R}}\left( {{\varepsilon _x}, {\varepsilon _y}, {\varepsilon _z}} \right) \times \left( {\begin{array}{*{20}{l}} {{x_\mathit{0}}}\\ {{y_\mathit{0}}}\\ {{z_\mathit{0}}} \end{array}} \right) $ | (5) |
式中,(x0,y0,z0) 为BIM顶点的局部坐标;R(εx,εy,εz) 为局部坐标到ENU坐标旋转矩阵;(X0,Y0,Z0) 和R (B0,L0,0) 分别为ENU到ECEF坐标系下的平移量和旋转矩阵。
本文根据该项目局部坐标系定义参数,通过Python对以上过程进行编程实现。在可视化时,将计算得到的旋转矩阵和平移量合成为4阶仿射变换矩阵,输入到Cesium中3DTileset对象的ModelMatrix属性中,即可在渲染时逐点进行坐标变换。实现效果如图 3所示,其中灰色部分即BIM所表现的立交桥,与实景三维模型所表现的周边房屋、地面融为一体。相比于人工三维建模,BIM模型具备更加精细的建筑构件结构并可针对构件进行属性关联。
 |
| 图 3 BIM与实景三维模型叠加效果 Fig.3 BIM and Real-Scene 3D Model Overlay Effect |
3 模型衔接处理
对于模型衔接区域的处理,本文采用对实景三维模型进行局部压平的方式:在WebGL渲染过程中,对衔接区域的实景三维模型三角网顶点进行降低,将其统一至设计的地面高度。整个压平处理的流程如图 4所示。
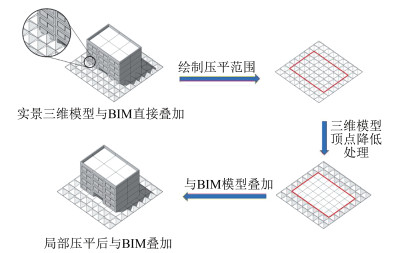 |
| 图 4 局部压平流程示意图 Fig.4 Partial Flattening Process Diagram |
通过修改WebGL渲染过程进行实现:事先采集叠加区域多边形轮廓及目标高度,通过调用Cesium中的Framebuffer对象渲染一张矩形Texture(叠加区域内为灰度为1,多边形外为0),将Texture与目标高度以WebGL Uniform属性的形式传递到实景三维模型中的Vertex Shader(WebGL的顶点渲染脚本)中,通过判断实景三维模型顶点坐标是否落在Texture灰度为1的区域内,进而将落在压平区域内的顶点高度进行降低。
局部压平的实现效果如图 5所示,对隧道口外的山体进行压平,即可直观表现隧道开挖后的实际效果。
 |
| 图 5 局部压平模拟开挖 Fig.5 Partial Flattening Simulation Excavation |
4 模型动态卷帘
为了在同一视图中直观对比BIM模型叠加前后效果,可通过动态卷帘的方式,对BIM与实景三维模型的显示进行控制:对视图进行左右分屏,在左屏中展示BIM与实景三维模型叠加效果、右屏中展示未叠加BIM的实景三维模型,并通过视图分隔UI组件拖动对左右屏宽度比例进行调整。
动态卷帘的实现是通过改写Cesium中3DTileset类的WebGL着色器(Shader)、配合第3节中介绍的顶点压平的方式来实现:首先,将分屏UI组件所在位置的屏幕坐标换算到WebGL坐标系下,并分别传递给BIM和实景三维模型的Vertex Shader,屏幕坐标系和WebGL坐标系之间关系见文献[13];其次,重写BIM模型的Fragment Shader(WebGL的片元渲染脚本),比较顶点gl_Position的水平坐标和分屏参数,如水平坐标大于分屏参数,通过Discard命令取消Fragment渲染;最后,重写顶点压平后的实景三维Vertex Shader,比较处于压平区域内顶点的gl_Position水平坐标和分屏参数,如水平坐标小于分屏参数,则执行顶点压平,反之则不执行。动态卷帘的实现效果如图 6所示,其中左侧为BIM模型叠加在实景三维模型上的效果;右侧为原始实景三维模型,分屏比例可拖动调整。
 |
| 图 6 卷帘切换实现效果 Fig.6 Roller Shutter Switching Effect |
5 结束语
BIM与GIS的集成,能够将建筑与环境信息融为一体,对室内外信息进行更加全面的数字化还原,对规划设计行业中的方案展示、方案比对具有重要的作用。本文以磁浮铁路项目为例,探讨了BIM与GIS的数据集成可视化流程及思路;基于开源的Cesium引擎,对BIM与实景三维模型集成中的坐标基准统一、模型衔接处理等实现方式进行介绍;介绍了用于对BIM与实景三维模型直观对比的动态卷帘实现方法。通过对BIM与GIS进行集成可视化,后续可实现更加高级的空间分析功能,进而为建筑设计、路桥施工、城市规划乃至CIM的建设提供平台支撑。
| [1] |
何清华, 钱丽丽, 段运峰, 等. BIM在国内外应用的现状及障碍研究[J]. 工程管理学报, 2012, 26(1): 12-16. DOI:10.3969/j.issn.1674-8859.2012.01.003 |
| [2] |
应申, 郭仁忠, 李霖. 应用3DGIS实现三维地籍: 实践与挑战[J]. 测绘地理信息, 2018, 43(2): 1-6. |
| [3] |
史艾嘉. BIM技术与GIS技术融合应用研究[J]. 价值工程, 2019, 38(21): 179-181. |
| [4] |
叶震, 许强, 刘谦, 等. 无人机倾斜摄影测量在边坡岩体结构面调查中的应用[J]. 武汉大学学报·信息科学版, 2020, 45(11): 1739-1746. |
| [5] |
陈玉龙. 多分辨率层次模型支持下的BIM-GIS集成可视化[J]. 测绘通报, 2018(12): 69-73. |
| [6] |
李鸿祥. 三维城市规划辅助决策支持系统的设计与实现[D]. 厦门: 厦门大学, 2013
|
| [7] |
吴志强, 甘惟. 转型时期的城市智能规划技术实践[J]. 城市建筑, 2018(3): 26-29. DOI:10.3969/j.issn.1673-0232.2018.03.004 |
| [8] |
吕慧玲, 李佩瑶, 汤圣君, 等. BIM模型到多细节层次GIS模型转换方法[J]. 地理信息世界, 2016, 23(4): 64-70. DOI:10.3969/j.issn.1672-1586.2016.04.012 |
| [9] |
贠法长, 曾传俊, 李旺民, 等. MXD/MDB文件基准转换方法研究及软件实现[J]. 测绘地理信息, 2019, 44(3): 117-121. |
| [10] |
范登科, 韩祖杰, 李华良, 等. 面向铁路信息化建设的BIM与GIS融合标准与技术研究[J]. 铁路技术创新, 2015(3): 35-40. |
| [11] |
刘茂华, 王岩, 孙秀波, 等. BIM与3DGIS结合实现室内、外三维一体化方法研究[J]. 科技通报, 2017, 33(7): 171-173. |
| [12] |
王越, 吴风华. BIM与GIS集成的三维建模方法研究[J]. 测绘与空间地理信息, 2018, 41(7): 192-194. DOI:10.3969/j.issn.1672-5867.2018.07.053 |
| [13] |
马军, 张石磊, 王莎莎. 基于BIM和GIS技术在管廊全生命周期的应用[J]. 智能建筑与智慧城市, 2018(12): 47-49. DOI:10.3969/j.issn.1671-9506.2018.12.022 |
| [14] |
曹浩泽. 3D Tiles定义解析与生产规范设计[D]. 武汉: 武汉大学, 2018
|
| [15] |
WebGiser: WebGL 3D概念讲解(坐标系)[EB/OL]. [2018-12-15], [2019-05-12]. https://www.jianshu.com/p/46706ebdf636
|
| [16] |
王海城, 徐进军, 王雯涛. 任意旋转角三维空间直角坐标转换的迭代算法[J]. 测绘地理信息, 2019, 44(1): 59-61. |
 2022, Vol. 47
2022, Vol. 47

