| 砂船量方的无人机低空摄影测量试验分析 |
2. 地球空间信息技术协同创新中心, 湖北 武汉, 430079;
3. 东华理工大学测绘工程学院, 江西 南昌, 330013
2. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China;
3. Faculty of Geomatics, East China Institute of Technology, Nanchang 330013, China
砂料在许多工程项目中需求巨大,且多数是由砂船经水上运输到施工现场的,因此砂船量方的效率和精度直接关系到项目的施工进度和成本控制。目前,砂船量方主要采用人工拉尺的方式,存在任务繁重、作业效率低、人员需求多等问题,因此需要采用合理、有效的方法来提高作业效率。张本平[1]利用全站仪进行土石方量数据采集并通过CASS软件进行计算;张红亮等[2]将GPS-RTK(GPS-real-time kinematic)技术结合方格网法进行土方测量;张荣华等[3]将三维激光扫描技术应用于土方量算。借鉴这些土方测量方法可以在一定程度上提高作业效率,但是使用全站仪或者GPS-RTK需要外业采集大量数据,而三维激光扫描仪价格昂贵,难以大规模推广。近年来,无人机(unmanned aerial vehicle, UAV)低空摄影测量技术发展迅速,能够在小区域内快速获取高分辨率影像,实现高精度、高效率、低成本的测量[4],在矿山监测[5]、国土资源管理[6]等领域得到广泛应用。
为验证无人机低空摄影测量方法能否满足砂船量方的要求,本文设计了两次试验,分别在陆地和砂船上采用无人机低空摄影测量技术对砂堆方量进行测量,并与人工测量的结果对比。结果表明,该方法效率高、成本低,能够满足砂船量方的精度要求,从而为砂船量方提供了一种全新高效的技术手段。
1 无人机量方关键技术采用无人机低空摄影测量方法进行砂船量方,首先使用无人机分别获取砂船在装砂前(空载)和装砂后(满载)的影像;然后对原始影像进行处理得到密集的三维点云数据,最后对点云进行插值计算得到载砂方量。其主要过程如图 1所示。
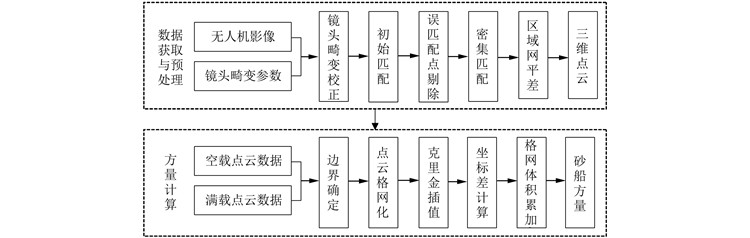 |
| 图 1 无人机量方技术流程 Fig.1 Technical Process of the Sand Volume Measurement by UAV |
1.1 镜头畸变校正
传统航空摄影测量通常使用量测型相机,摄影中心与影像的相对位置经过严格的检校,内方位元素固定,摄影后产生的光学畸变小。但是无人机搭载的航空摄影测量设备大多是非量测相机,获取的影像存在较大的光学畸变。因此,在使用这些影像进行高精度的测量之前,必须进行必要的镜头畸变校正。文献[7]提出了一种基于棋盘格模板的相机标定方法,只需要对棋盘格模板从不同方向拍摄多幅影像即可进行标定。由于棋盘格模板制作简单,使用方便,同时考虑砂船量方的精度要求,本文采用该方法进行镜头畸变校正。
采用齐次坐标表示针孔模型的投影变换为:
| $ \lambda \left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1}}&{{\mathit{\boldsymbol{r}}_2}}&{{\mathit{\boldsymbol{r}}_3}}&\mathit{\boldsymbol{t}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} X\\ Y\\ Z\\ 1 \end{array}} \right] $ | (1) |
式中,[u v 1]T为模板平面上的点投影到图像平面上对应点的齐次坐标;[X Y 1]T为模板平面上点的齐次坐标;λ为比例因子;K为相机的内方位矩阵;[r 1 r 2 r 3]和t分别是相机坐标系相对于世界坐标系的旋转矩阵和平移向量。
对于平面模板而言,Z分量恒为零,因此式(1)可以表达为:
| $ \lambda \left[ {\begin{array}{*{20}{c}} u\\ v\\ 1 \end{array}} \right] = \mathit{\boldsymbol{H}}\left[ {\begin{array}{*{20}{c}} X\\ Y\\ 1 \end{array}} \right] $ | (2) |
式中,H =[h 1 h 2 h 3]= K [r 1 r 2 t],称为同形矩阵。
根据旋转矩阵的性质,即r1T r 2=0,|| r 1|| = || r 2 ||=1,每幅影像可以获得以下两个对内方位矩阵的约束条件:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{h}}_1^{\rm{T}}{\mathit{\boldsymbol{K}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{h}}_2} = 0\\ \mathit{\boldsymbol{h}}_1^{\rm{T}}{\mathit{\boldsymbol{K}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{h}}_1} = \mathit{\boldsymbol{h}}_2^{\rm{T}}{\mathit{\boldsymbol{K}}^{ - {\rm{T}}}}{\mathit{\boldsymbol{K}}^{ - 1}}{\mathit{\boldsymbol{h}}_2} \end{array} \right. $ | (3) |
这两个约束条件可以用来求解内方位矩阵,由于内方位矩阵有5个未知参数,所以至少需要3张影像才能进行标定。
1.2 影像数据采集影像数据通过无人机低空摄影的方式进行采集。对砂船进行拍摄时,为保证影像质量,要求影像必须覆盖全船宽度,且影像中船宽d应大于影像宽度D的60%,如图 2所示。因此,真实船宽l也应大于影像覆盖实地宽度L的60%,即
| $ H = \frac{L}{D}f $ | (4) |
 |
| 图 2 影像覆盖要求 Fig.2 Requirement of Image Coverage |
式中,f为相机焦距。
为了后续无人机影像数据处理的顺利完成,必须对无人机获取的影像进行质量检查,剔除不合格的影像,检查主要针对以下方面:
1) 影像的色调。要求影像清晰,色调一致,反差适中,像片上不应有妨碍测图的阴影。
2) 影像重叠度。由于砂堆表面起伏较大,为了保证像片立体量测与拼接,航向重叠度要求不小于80%。
1.3 数据处理获取合格的影像后可进行内业数据处理,主要步骤如下:
1) 利用镜头畸变改正参数对原始影像数据进行畸变修正;
2) 对修正后的影像进行重采样,缩小一定倍数,并建立金字塔影像,进行SIFT(scale-invariant feature transform,尺度不变特征变换)匹配得到初始的匹配点[8];
3) 由于初始匹配点中存在一定数量的误匹配点,直接进行相对定向解算的结果精度不高,因此先利用RANSAC方法剔除误匹配点,再进行相对定向解算[9];
4) 在左片影像上,采用Harris亚像素角点检测法来提取特征点,再根据这些特征点采用最小二乘法在右片影像上搜索同名点进行加密匹配,得到更为密集的三维点云数据[10];
5) 进行区域网平差,得到点云在物方坐标系下的三维坐标;
6) 以Z坐标值为属性值对点云数据进行重采样,将船舱区域划分为许多等间距的方格网,插值得到各格网点的Z坐标值;
7) 以各格网点为中心,将满舱和空舱的Z坐标值相减得到的坐标差作为高、相应的方格作为底,构成一个小长方体来计算体积,累加所有小长方体体积即可得到最终的方量。
2 试验与分析为了验证无人机低空摄影测量方法进行砂船量方的准确性和科学性,设计并进行了两次试验。试验所用无人机为DJI PHANTOM 4 PRO+,属于四旋翼微型低空无人机,搭载的影像传感器为1英吋CMOS,有效像素为2 000万。
2.1 地面试验第一次试验在某砂厂进行,为了获取更为准确的砂堆方量,在一处平坦空地上堆出较为规则的砂堆,如图 3(a)所示,整个砂堆呈台体状,易于人工量算。使用无人机分别采集堆砂前和堆砂后该区域的影像,并采用人工拉尺方式对规则的砂堆进行测量。之后破坏该砂堆的规则性,使其形状不再规则,如图 3(b)所示,再次使用无人机采集砂堆影像。
 |
| 图 3 规则和不规则的砂堆 Fig.3 Regular Sand Pile and Irregular Sand Pile |
1) 人工测量误差分析。人工测量时,量距使用的是皮尺,相对精度约为1/500[11],现分析其对砂堆方量计算结果的影响。本次试验砂堆平面尺寸如图 4所示,L1=8.215 m,L2=8.443 m,L3=15.297 m,L4=15.722 m,高度h=2.973 m。
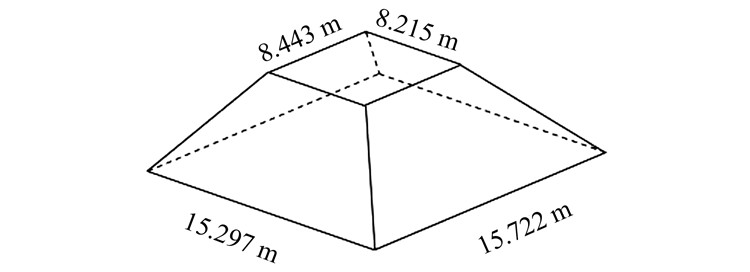 |
| 图 4 砂堆尺寸 Fig.4 Size of Sand Pile |
根据台体体积计算公式可知,砂堆方量V为:
| $ V = \frac{h}{3}\left( {{L_1}{L_2} + {L_3}{L_4} + \sqrt {{L_1}{L_2}{L_3}{L_4}} } \right) $ | (5) |
对V全微分,得:
| $ \begin{array}{l} {\rm{d}}V = \frac{h}{3}\left( {{L_2} + \frac{{{L_2}{S_2}}}{{2{S_3}}}} \right){\rm{d}}{L_1} + \frac{h}{3}\left( {{L_1} + \frac{{{L_1}{S_2}}}{{2{S_3}}}} \right){\rm{d}}{L_2} + \\ \frac{h}{3}\left( {{L_4} + \frac{{{L_4}{S_1}}}{{2{S_3}}}} \right){\rm{d}}{L_3} + \frac{h}{3}\left( {{L_3} + \frac{{{L_3}{S_1}}}{{2{S_3}}}} \right){\rm{d}}{L_4} + \\ \frac{{{S_1} + {S_2} + {S_3}}}{3}{\rm{d}}h \end{array} $ | (6) |
式中,S1=L1L2;S2=L3L4;S3=
根据误差传播率可得V的方差为:
| $ \begin{array}{l} \sigma _V^2 = \frac{{{h^2}}}{9}{\left( {{L_2} + \frac{{{L_2}{S_2}}}{{2{S_3}}}} \right)^2}\sigma _{{L_1}}^2 + \frac{{{h^2}}}{9}{\left( {{L_1} + \frac{{{L_1}{S_2}}}{{2{S_3}}}} \right)^2}\sigma _{{L_2}}^2 + \\ \frac{{{h^2}}}{9}{\left( {{L_4} + \frac{{{L_4}{S_1}}}{{2{S_3}}}} \right)^2}\sigma _{{L_3}}^2 + \frac{{{h^2}}}{9}{\left( {{L_3} + \frac{{{L_3}{S_1}}}{{2{S_3}}}} \right)^2}\sigma _{{L_4}}^2 + \\ {\left( {\frac{{{S_1} + {S_2} + {S_3}}}{3}} \right)^2}\sigma _h^2 \end{array} $ | (7) |
代入数据可得方量中误差σV=±1.277 m3,而人工测量所得方量为435 m3,因此方量相对中误差为0.3%。可见,人工拉尺测量砂堆尺寸对最终方量计算结果影响很小。
2) 试验结果与分析。本次试验以不同测量方式得到的结果如表 1所示,绝对偏差等于无人机低空摄影测量结果减去人工测量结果,相对偏差等于绝对偏差除以人工测量结果。
| 表 1 第一次试验结果对比 Tab.1 Comparison Results of the First Experiment |
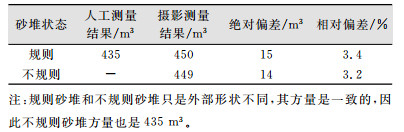 |
从表 1可以看出,低空摄影测量所得的两次结果偏差为1 m3,表明该方法结果稳定,且不受砂堆形状的影响;低空摄影测量与人工测量结果两次的相对偏差分别为3.4%和3.2%,满足一般工程中要求的5%的允许误差[12],表明无人机低空摄影测量方法用于量方具有可行性,能够利用影像数据通过软件处理快速、准确地得到相应的方量。
2.2 砂船试验砂船在水域中受到水流等因素影响,即使抛锚也并非完全静止,测量环境有别于陆地。因此第二次试验在砂船上开展。当砂船抛锚在水中时,使用无人机分别采集其空载影像和满载影像,然后将砂船上不规则的砂堆平整为规则的台体,再利用无人机低空摄影和人工拉尺的方式对其进行测量。
图 5为平整前、后的砂堆示意图。
 |
| 图 5 平整前和平整后的砂堆 Fig.5 Sand Pile Before and After Leveling |
试验结果如表 2所示,绝对偏差等于无人机低空摄影测量结果减去人工测量结果,相对偏差等于绝对偏差除以人工测量结果。
| 表 2 第二次试验结果对比 Tab.2 Comparison of the Second Experiment Results |
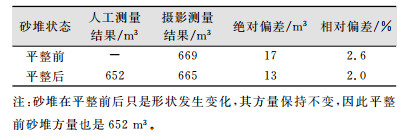 |
从表 2可以看出,低空摄影测量两次结果的偏差为4 m3,与人工测量结果的相对偏差分别为2.6%和2.0%。而且采用无人机低空摄影测量方法进行砂船量方,可不受场地障碍的影响,也不需要多人协同作业,同时测量成果数据信息化程度高,可以提供由影像匹配生成的密集点云,能够直接导入软件自动计算,操作方便快捷。因此,无人机低空摄影测量方法可以满足砂船量方高效率、低成本的作业需求。
3 结束语本文研究了采用无人机低空摄影测量技术进行砂船量方的技术流程和数据处理方法,通过与人工测量结果对比,其精度优于4%,证明了利用无人机低空摄影测量方法进行砂船量方的可行性。无人机低空摄影测量技术具有机动性强、劳动强度低、采集速度快、生产成本低、信息化程度高等优点,而且原始数据可以反复核查,结果的客观性强于人工测量,为砂船量方提供了一种全新高效的技术手段。
| [1] |
张本平. 基于全站仪和CASS软件的土石方量计算[J]. 科技创新导报, 2011(23): 120. DOI:10.3969/j.issn.1674-098X.2011.23.098 |
| [2] |
张红亮, 胡波, 蔡元波. GPS-RTK技术在土方测量中的应用[J]. 城市勘测, 2008(5): 83-85. DOI:10.3969/j.issn.1672-8262.2008.05.021 |
| [3] |
张荣华, 李俊峰, 林昀. 三维激光扫描技术在土方量算中的应用研究[J]. 测绘地理信息, 2014, 39(6): 47-49. |
| [4] |
万刚, 余旭初, 布树辉, 等.无人机测绘技术及应用[M].北京: 测绘出版社, 2015: 14-15
|
| [5] |
章梦霞, 郑新奇, 刘波. 无人机影像支持的矿区开采动态监测方法[J]. 测绘通报, 2017(10): 43-47. |
| [6] |
肖亮明, 陈建忠. 无人机航测技术在国土资源管理中的应用[J]. 测绘地理信息, 2017, 42(5): 96-99. |
| [7] |
Zhang Z Y.Flexible Camera Calibration by Viewing a Plane from Unknown Orientations[C]. Proceedings of the 7th International Conference on Computer Vision, Kerkyra, Greece, 1999
|
| [8] |
刘晓莉. 一种基于改进的SIFT特征点算法的无人机影像快速匹配研究[J]. 测绘与空间地理信息, 2014, 37(9): 207-210. DOI:10.3969/j.issn.1672-5867.2014.09.066 |
| [9] |
谢萍, 邹峥嵘, 肖奇. 基于Harris角点和SIFT特征的近景影像匹配[J]. 测绘科学, 2012, 37(4): 107-110. |
| [10] |
何海清.低空摄影测量航带重构及数据处理方法研究[D].武汉: 武汉大学, 2013
|
| [11] |
刘云伟, 冯仲科, 邓向瑞, 等. 同一铅垂面两次设站法树高测量及其精度分析[J]. 北京林业大学学报, 2007(S2): 57-60. |
| [12] |
中华人民共和国国家能源局.水利水电工程施工测量规范: DL/T5173-2012[S].北京: 中国电力出版社, 2012
|
 2020, Vol. 45
2020, Vol. 45


